Методы и схемы анализа спектров сигналов на основе обобщенной модификации преобразования Фурье

Для анализа спектров методом преобразования Фурье (ПФ) различных типов сигналов может использоваться несколько схем: обычное ПФ (непрерывного сигнала), ряды Фурье, преобразование Фурье дискретного времени, дискретное ПФ [1, 2]. Вместе с тем анализ Фурье корректно обеспечивает получение частотных компонент сигнала только на квазистационарных интервалах, а в практических приложениях достаточно часто встречаются информационно-измерительные системы (ИИС), в которых сигналы нестационарны. В связи с этим для обработки таких сигналов используются методы время-частотных и время-масштабных (вейвлет-) преобразований [3–6]. Для этой же цели может применяться анализ на основе модифицированной формы преобразования Фурье — вращаемого ПФ, который позволяет выявить смешанные временные и частотные компоненты сигнала.

Вращаемое преобразование Фурье (ВПФ) имеет собственные (отличные от ПФ) свойства, в том числе аддитивность углового параметра ВПФ, связь ВПФ с время-частотными преобразованиями, с преобразованием Радона и с традиционным ПФ. Для операции ВПФ сигналов, умножения двух сигналов в области ВПФ (или свертки сигнала с импульсой передаточной функцией) также свойственны особые правила [7–10].

Для обработки сигналов различных типов на основе обобщенной модификации Фурье метод ВПФ располагает двумя схемами анализа. Это собственно ВПФ [7] и дискретное вращаемое преобразование Фурье (Д_ВПФ) [10, 11]. Такие схемы анализа используются для непрерывных и дискретных сигналов, и результат преобразований соответственно непрерывный и дискретный. Если следовать пути и логике развития схем традици- онного ПФ, то представляется целесообразным введение еще двух новых схем анализа сигналов методом ВПФ — рядов вращаемого преобразования Фурье (Р_ВПФ) и вращаемого преобразования Фурье дискретного времени (ВПФ_ДВ).1)

ПРЕОБРАЗОВАНИЕ СИГНАЛА ВРАЩАЕМЫМ ПРЕОБРАЗОВАНИЕМ ФУРЬЕ

Ядро преобразования по методу непрерывного ВПФ определяется выражением:

K a ( t , U ) = j

' 1- j ctg а 2 п

j [( t ² + u ²) /2]ctg а - jtu cosec а

если а не кратно п ;

3 ( t - u ), если а кратно п ;

S(t + u), если а + п кратно 2п, где α — угол вращения (параметр ВПФ).

Прямое S α ( u ) и обратное ВПФ сигнала s ( t ) выражаются с помощью ядра К _а ( t , и ) соотношениями (2) и (3):

f +^

5 ( t ) К а ( t , U )d t ,              (2)

—га

+^

5 ( t ) = J S „ ( U ) K - a ( t , u )d u.            (3)

-TO

Свойства непрерывного ВПФ приведены в работах [9, 12]. При построении новых схем анализа сигнала методами рядов ВПФ и ВПФ дискретного времени за основную область параметра а , определяющего вращение время-частотной плоскости, принят интервал а е (0, п /2).

РЯДЫ ВРАЩАЕМОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ

Частотный спектр периодического сигнала состоит из последовательности импульсов, поэтому такой сигнал представляется в форме ряда Фурье (РФ) (4) , коэффициенты разложения которого определяются выражением (5):

5 ( t ) = S     Ce n ⁰ ,             (4)

C n = 1 J 5 ( t ) e -^{jnt m 0} d t ,                (5)

TT где 5(t) — периодический сигнал с периодом Т; юо =(2п / T); {Cn}n=-~,...,-i,o,i,...,~ — коэффициенты разложения сигнала в РФ.

Разложение в РФ может использоваться для двух классов непрерывных сигналов:

• •    так может представляться апериодический сигнал 5 ( t ), определенный на некотором интервале [0, T ]; в этом случае РФ сходится к периодическому расширению 5 ( t ) на область как внутри, так и вне [0, T], т. е. сходится к 5 ( t + n ), n = 0 , ± 1 , ± 2 , ...;

• •    кроме того, РФ может использоваться для представления периодического сигнала (с любым периодом).

Для построения схемы рядов вращаемого преобразования Фурье (Р_ВПФ) удобно сначала получить ортогональный базис. Для этого используется аналогия с традиционным ПФ. В случае обычного ПФ базисная функция — синусоида, в результате ПФ дает 8-образный импульс. При использовании аналогичной взаимосвязи базисные функции ВПФ могут быть найдены так.

• •    Для импульсной функции S ( t - nt ₀ ) , принадлежащей области ВПФ с параметром а , ее прообраз во временной области выражается с помощью обратного вращения время-частотной плоскости, т. е. путем применения ВПФ с угловым параметром - а :

ВПФ-а [S(t - nt0 )] =

• /1 + j ctg a - j [ ( t ² + ( nt ₀ ) ² ) /2 ] ctg a + j ( nt ₀ ) t cosec a

• = —-—-—e        ^J          . (6)

• V    2 п

Этот прообраз может служить в качестве базисных функций для Р_ВПФ, т. е. базисным набором может быть набор V „ (t)}„___   0 „ „, элементы ко, n          n ,..., , , +,..., торого определяются соотношением (7):

V a , n ⁽ t ) =

= /1 + j ctg a e - j [ ( t ² + ( nt 0 ) ² ) /2 j ctg a + j ( nt 0 ) t cosec a

• V    2 п

Параметр 1 ₀ называется центральной частотой базисного сигнала (7) в области ВПФ. Такое его название связано с установленным ниже условием 1 ₀ = 2 п (sin а / T ), которое необходимо для взаимной ортогональности базисных функций и которое показывает "пропорциональность" 1 ₀ 1/ T , где T — область задания анализируемого сигнала.

• •    Базисные функции-сигналы у ВПФ являются так называемыми сигналами с быстро изменяющейся частотой (СБИЧ); это апериодические сигналы, которым не может быть приписана какая-либо определенная частота. Поскольку сумма апериодических компонент не может быть периодической, рядами ВПФ представляют только сигналы, определенные на конечной временной области ("финитные" сигналы).¹⁾

• •    Набор базисных сигналов (БС) (7) для разложения в Р_ВПФ при определенных условиях является ортонормальным. Это показывает интегри-рованиепары²⁾ БС на интервале [ - T /2, T /2 ] :

T /2

J V a , m ⁽ t Va n, ⁽ t ^)d t =

• - ( T /2)

i Г// \2 / \2\ "I       ( T /2)cosec a

= ¹ e ^{j [ (( nt} 0 ^{) - (} mt 0 ^{)) /2} J ^{ctg a}       f        e j ( m - n ) 1 0 Г d t" _; (8)

2П                          J                   ;

-(T/2)coseca из (8) получаем

T /2

J V a , m ⁽ tV«,„ ⁽ t ^)d t =

- ( T /2)

T cosec а

--------             при m = n ;

2 п

----------х j 2п( m - n) tо х e [((nt0 )2-(mt о )2 )/2] ctg a (m _ n) t o ( t/2)cosec а x x{eJ(m-n)t0 Tcosecа }          при m ^ n.

(В преобразованиях, ведущих к получению выражений (8) и (9), использована замена переменных t = t cosec а ).

• • Чтобы ф _{а п} удовлетворяли условию ортогональности, правая часть в (9) при m ^ n должна быть равна нулю. Это условие может быть удовлетворено, только когда t ₀ = 2 п ( sin а / T ) . Кроме то

го, можно разделить каждую ф _{а n} на величину (2 п ) ^{- 1} Tcosec а и получить ортогональный базис ^{ Ф а ,n ^} для ^Р_ВПФ:

• -          РФ „( t )      /sin а + j cos а

• ф (А = ,   ’ г = . --------2 х

^Фа • "^v

TcosecаV

V 2п х exp{-j[(t2 +(n(2n/T)sinа)2/2)]ctgа +

+jnt (2n / T)}, где n = -”,...,-1,0,1,...,” . Так что набор (множество) {...,фа._1,фа_0,фа_х,...} составляет базис ортогональных сигналов.

Приведем еще два замечания.

• 1)    Текущее значение "мгновенной" частоты БС может быть получено вычислением производной от фазы, поэтому текущая частота БС определяется выражением

^ю _а , _n ( t ) = - 1 ctg а + 2 n n / T .         (11)

Из (11) видно, что каждый БС является СБИЧ с постоянной скоростью изменения частоты ( - t ctg а ).

• 2)    Представление (финитного) сигнала в виде Р_ВПФ интерпретируется как разложение на составляющие элементы (гармоники) — СБИЧ.

Таким образом, разложение сигнала $ ( t ) в ряд по вращаемому преобразованию Фурье со значением углового параметра а представляется соотношением:

„                    Г      / sin а + j cos a

$ ( t ) = X ^С<м P « n ( t ) = X ^С<м J ---- x

• n = -^                  n = —^ ^       1        ^х

exp { - j ( t ² + ( n ( 2 n / T ) sin а ) ² ) /2 ctg а

A

+ jnt ( 2 n / T )}

t e [ - T /2, T /2 ] ,       (12)

где С _а „ — коэффициенты разложения в Р_ВПФ с параметром а.³⁾

Коэффициенты разложения сигнала в Р_ВПФ определяются выражением (13)4):

T /2

^С а , n = /    $ ⁽ t^{) ф}а,„ ⁽ t ^)d t =

- ( T /2)

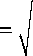
sin а + j cos а T

T /2

I

- ( T /2)

$ ( t ) x

x exp { j ( t ² + ( n ( 2 n / T ) sin а ) ² /2 ) ctg а

-

• - jnt ( 2 n / T ) d t . (13)

Разложение в Р_ВПФ может использоваться для представления апериодичного сигнала $ ( t ), который определен на конечном интервале (в (13) принят интервал [ - T /2, T /2 ] ).

Свойства Р_ВПФ систематизированы Пэйем— Йехом [11, 13] и показаны в табл. 1. Эти свойства в определенной степени сходны со свойствами ВПФ непрерывного сигнала. Немного позднее (после анализа ВПФ_ДВ) будет проведено сопоставление свойств сдвига и модуляции для Р_ВПФ и для рядов обычного преобразования Фурье, а также сопоставление свойства ВПФ_ДВ и ПФ_ДВ. Такие сопоставления будут даны в табл. 3.

Этими же авторами установлена взаимосвязь и соотношение между коэффициентами разложения сигнала в Р_ВПФ и значением ВПФ самого сигнала (при определенным образом масштабированном аргументе ВПФ):

2 n sin а

T

с ( 2п . __i 5„ n —sin а , а I T I

где С _а n — коэффициент разложения сигнала $ ( t ) в Р_ВПФ S _a — ВПФ этого сигнала.

Из (14) видно, что интервал отсчетов зависит как от α (параметра ВПФ), так и от T (длины интервала, являющегося областью определения сигнала). При этом, когда интервал Т для вычисления Р_ВПФ значительно возрастает (в предельном случае ^ ” ), интервал отсчетов коэффициентов разложения стремится к нулю. Поэтому по мере возрастания интервала Т Р_ВПФ будет постепенно переходить просто в ВПФ сигнала, а в предельном случае ( T ~ ” ) Р_ВПФ эквивалентен вращаемому преобразованию Фурье сигнала.

ВРАЩАЕМОЕ ПРЕОБРАЗОВАНИЕ ДИСКРЕТНОГО ВРЕМЕНИ

Известный метод ПФ дискретного времени (ПФ_ДВ) обеспечивает процедуры вычисления частотных компонент дискретного сигнала. Обычное определение ПФ_ДВ представляется в форме с нормализацией частоты [2]. Это придает методу независимость от интервала квантования анализируемого сигнала и приводит выражение ПФ_ДВ к формуле для периодической функции с периодом 2 π .

ПФ_ДВ без нормализации частоты дает периодический результат преобразования с периодом 2 π / T 1 , где T 1 — интервал дискретизации сигнала.

Определение прямого и обратного ПФ_ДВ без нормализации частоты отсчетов сигнала выражается соотношениями (15) и (16):

S( т ) = _А T¹^ 5 $ ( n ) e"^Мх, (15)

V 2 n n =-~

I T П / T

• $ ( n ) = TA J S(_Ю ) e^d m . (16) V 2 n - ( _K / t )

При формировании ВПФ_ДВ, являющегося обобщением обычного преобразования Фурье дискретного времени, необходимые преобразования удобнее осуществлять на основе выражений (15) и (16) (т. е на основе определения прямого и обратного ПФ_ДВ без нормализации частоты отсчетов сигнала).

Построение метода ВПФ_ДТ использует два положения, первое из которых традиционное, а второе имеет специфику, свойственную процедурам аналитического развития схемы ВПФ_ДТ:

• •    сигнал $ ( n ) получен из сигнала $ ( t ) с ограниченной частотной полосой путем дискретизации его по времени с интервалом T 1 ;

• •    при построении ВПФ_ДТ роль временной и частотной осей у Р_ВПФ взаимно заменяется; делается это для удобства определения ВПФ_ДТ; это значит, что дискретные отсчеты во временнóй области трактуются как коэффициенты Р_ВПФ в частотной области.

Табл. 1. Свойства рядов вращаемого преобразования Фурье

Вид свойства Р_ВПФ	Формализованное представление свойства
Изменение отсчета времени сигнала	Р_ВПФ[ $ (- t )] ^ C a (- n )
Комплексное сопряжение сигнала	Р_ВПФ[ $ ( t )] ^ j ( C -a,n ) *
Сдвиг сигнала по времени на величину τ (кратную относительно (2 п tg а )/ T )	т = k (2 п tg а )/ T ;    к - целое; t 0 = (2 п sin а )/ T ; ■ т 2 ■ „ - / —sin а cos а - /nt т sin а Р_ВПФ[ $ ( t - т )Э С о „ - ке 2
Модуляция сигнала ( $ ( t ) ^ $ ( t ) ejmt 0 ‘ )	( mt )2 .                           - / -—°2—sin а cos а + /mntn cos а Р_ВПФ[ $ ( t ) e- 0 ' ] ^ С а ,, . - m „. а , =   2                 , где t о =2п (sin а ) /1 ; ( n - m sin а ) — целое
Масштабирование сигнала ( $ ( t ) ^ $ ( ct ))	1          1                   j ( nt 0 ) ctg в L 4-sA ) РВПФ[ $ ( ct )] ^ C.-Tc x, A- 1 - j clg а e 2 I s-2 а | -               e , n     Vsin в у C - j ctg а
Соотношение Парсеваля	а ^ m n ; m — целое; 5 ” = _ | С а Л |2 = J t | $ ( t ) |2 d t

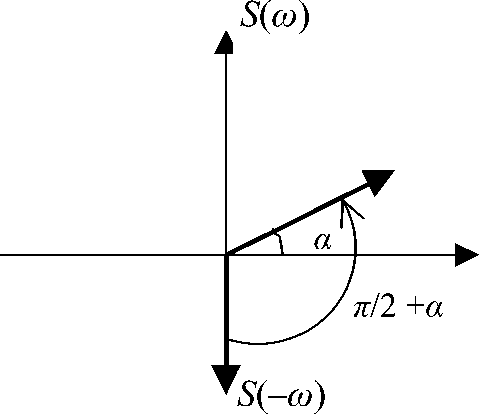
К концепции использования спектра сигнала в виде S (– ω ) при построении преобразований для получения вращаемого преобразования Фурье дискретного времени

га „

= s k(

, cos a - j sin a ^{( я /2) + a} , ⁿ\      2 я / T 1

х exp j ( ( to ² + ( nT cos а ) 2 ) /2 ) tg a + jn to T 1 - . (17)

• С помощью (13) вычисляются коэффициенты разложения Р_ ВПФ:

D a [ n ] = C ( я / T

' ( я /2) + a , n

-I

f ⁵ ( to )

( я / T )

х exp - j

T

—(cos a + j sin a ) х 2 я

to ² + n ² T cos² a

tg a х

х exp[ - jn to T ]d to ;

далее из (18)

D a [ n ] =

Логическая последовательность построения ВПФ_ДТ включает следующие этапы.

• •    Выполняется разложение спектральной функции S ( –ω ) сигнала s ( t ) в Р_ВПФ с параметром ( π /2 + α ).⁵⁾ Эта концепция показана на рисунке. Выбор спектра S (– ω ) (вместо S ( ω )) объясняется тем, что разложение S (– ω ) в Р_ВПФ с положительным значением параметра (( π /2) + α ) может облегчить сложность преобразований, связанных с построением схемы ВПФ_ДВ [13].

• •    С помощью (12) осуществляется представление спектра сигнала с дискретными отсчетами в форме выражения (17):

  T

  = 2 _xws a + j sin a exp

  

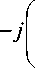
  n ² T "

  
  
  
  
  

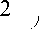
  sin a cos a х

  
  

_га            я / T 1

х ^ s [ k ] f exp [- j( to ²/2)tg a^

^{k =-га}       - ( я / T )

х exp [ j to T 1 ( k - n ) ] d to                              ⁽¹⁹⁾

и затем из (19)

D a [ n ] =

T^ 1 1 - j ctg a

2 V   2 я

^cos a х

га

5( -to ) = Х C ( я /2) + а Л n = -га                 '

■ I я . V . I я . 1 sin —+а + j cos —+а 22

—^z х 2 я / T 1

х exp

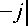
n ² T ₁ 2

sin a cos a

х exp -

2я

2 я / T 1

sin ( ( я /2) + a )

х1/(2ctg ((я/2) + а)) + jnto

2я

2 я / T 1

х

5) Отметим, что спектральная функция берется для про-

тивоположного отсчета аргумента, т. е. S ( –ω ) .

га х^ ^[ k ] Г( n, k ,a),

-га

где D _a [ n ] является ВПФ_ДВ дискретного сигнала s [ k ]; a ^ т я + я /2 ( m — целое). Кроме того, в (20) введено обозначение для функции Г( n , k, a ), которая выражается через функцию плотности распределения вероятности (ФРВ) ("функцию ошибок"):

Г( n , k , a ) =

= - - ФРВ j

-n tg a + 7 12 ( n - k ) 7 1V" ² j tg a

+ ФРВ j ^{n tg a} + ^{T ( n} - ^k )

V Tj J

■^{x ex}P ( j ( ⁷ ( ^{k - n} ) 2 /2 ) ctg ^a ) ,    ⁽²¹⁾

где ФРВ (для гауссовой плотности — так называемого нормального распределения) определяется известным выражением

x

ФРВ( x ) = —j= f exp( - u ²)d u .

V ⁿ 0

Соотношение (18) обеспечивает метод для вычисления ВПФ_ДВ на основе сигнала, заданного в частотной области. Соотношение (20) — способ получения ВПФ_ДВ из временнóй формы сигнала ({ s [ k ] k =...–1,0,1,… }).

При a = 0 результат преобразования D _a [ n ] будет соответствовать начальному сигналу x [ k ]. Однако при α = mπ + π /2 преобразование становится обычным преобразованием Фурье дискретного времени.

Обратное ВПФ_ДВ вычисляется на основе соотношения:

T 1 + j ctg a s [ n ] = — —-—-—

2 n

x exp

n² 7 12 '

/ sin a cos a

V

^

■ У D [ k ] Г( n , k , -a ),

—^

где вспомогательная функция Г( n , k, a ) определена соотношением (21).

Из (23) видно, что первоначальный сигнал может быть восстановлен из ВПФ_ДВ со значением параметра (– α ). Подобно тому как в случае Р_ВПФ при значительном уменьшении интервала дискретизации T 1 (в пределе при T 1 → 0 ) результат ВПФ_ДВ может быть получен с использованием отсчетов ВПФ:

D _a [ n ] = V T cos a S _a ( nT₁ cos a ), (24) где S _a ( • ) — ВПФ сигнала со специальной формой отсчетов при параметре α .

Из (24) видно, что расстояние между отсчетами ("интервал дискретизации") ВПФ_ДВ будет становиться меньше, когда угловой параметр α приближается к значению, равному ( mπ+ ( π /2)) с целым m . Если параметр α равен ( mπ+ ( π /2)), то расстояние между отсчетами ВПФ_ДВ становится нулевым. Это отвечает известному результату, состоящему в том, что в этом случае выход ВПФ_ДВ является непрерывной функцией.

Свойства ВПФ_ДВ, систематизированные в табл. 2, подобны свойствам Р_ВПФ, за исключением того, что угловой параметр должен быть изменен.

Аналогично случаю Р_ВПФ свойства ВПФ_ДВ, относящиеся к модуляции и к сдвигу, выполняются при некоторых ограничениях, и они отдельно собраны в табл. 3 с сопоставлением их со свойствами этого типа у ПФ_ДВ. В первой части табл. 3 (она упоминалась выше) показаны свойства, относящиеся к модуляции и к сдвигу для Р_ВПФ, дано их сопоставление с соответствующими свойствами РФ и вид ограничений, при которых эти свойства выполняются.

В табл. 4 показаны типы сигналов различных схем ВПФ, разработанных до самого последнего времени [13]. Для сравнения в последнем столбце таблицы показаны типы схем традиционного преобразования Фурье. Среди четырех таких схем

• •    обычное (ПФ), являющееся первичным методом;

• •    РФ — дискретные, апериодические;

• •    ПФ_ДВ — непрерывные, периодические;

• •    Д_ПФ, которое определено для дискретизованного по времени и периодического сигнала и дает в результате дискретный и периодический спектр [2]. Поэтому типы первоначальных сигналов и преобразований для Д_ПФ относятся как к дискретизованному, так и периодическому видам.

Табл. 2. Свойства вращаемого преобразования Фурье дискретного времени (ВПФ_ДВ)

Вид свойства ВПФ_ДВ	Формализованное представление свойства
Изменение отсчета аргумента	ВПФ ДВ[ s ( -n )] ^ D a [ -n ]
Комплексное сопряжение сигнала	ВПФ ДВ[ s * ( n )] ^ j ( D *—a [ n ])
Сдвиг сигнала по времени на величину т	• ( т^ )2 •  - _„2 • / ---0— sin a cos а - ттюп sin а ВПФ_ДВ[ s ( n - т )] ^ D a [ n - т cos а ] e 2              , to 0 = T cos a и ( n - т cos а ) — целые
Модуляция сигнала ( s [ n ] -> s [ n]e jn T T1 )	■ ( т )2 ■ „                     „ :и- т                      - /    sin а cos а + / и^т cos а ВПФ_ДВ[ s [ n ] e ' \ ^ D a [ n - к ] e 2              , т = к x T ctg а , где переменная к — целое число
Соотношение Парсеваля	( а ^ т п + п /2) и т — целое -> E s [ n ]|2 = E D a [ n ] 2 n =-∞           n =-∞

Табл. 3. Ограничения для свойств сдвига и модуляции у Р_ВПФ и ВПФ_ДВ

Вид преобразования	Свойство сдвига	Свойство модуляции
Ряд вращаемого преобразования Фурье (Р_ВПФ)	s ( t - т ), т = к (2 п / T )tg а , к — целое	s ( t ) e , ν = k(2π/T), k — целое
Ряд Фурье	s ( t - т ), т — произвольное	s ( t ) e, v = к ( 2n/T ), к — целое
Вращаемое преобразование Фурье дискретного времени (ВПФ_ДВ)	s ( n - т ), т и ( т cos а ) — целые числа	s ( n ) e^ T , v = kT 1 cos а , к — целое
Преобразование Фурье дискретного времени (ПФ_ДВ)	s ( n - т ), τ — целое	s ( n ) e^ T , v — произвольное

Тип ВПФ_ДВ, построенный по обсуждавшейся выше логике, является дискретным и апериодическим в области ВПФ (при угловом параметре 0 <  а <  п /2) и имеет там "бесконечную область определения".⁶ ) Кроме того, получаемая для

ВПФ_ДВ дискретизация (интервал между отсчетами) составляет T 1 cos а . Причем, если а = тп + + п /2, то интервал отсчетов ВПФ_ДВ становится нулевым (точнее стремится к нулю) и ВПФ_ДВ будет сводиться к обычному дискретному преобразованию Фурье (ДПФ). Близкая ситуация возникает и в случае Р_ВПФ: интервал отсчетов составляет 2 п sin а / T и он становится нулем при а =тп , так что в результате получается непрерывный сигнал. (Для полноты сопоставления различных схем (набора методов), связанных с ПФ, ДПФ, Р_ПФ, ВПФ_ДВ, последняя строка в табл. 4 показывает тип данных дискретного вращаемого преобразования Фурье (Д_ВПФ), которое детально не обсуждалось в нашей статье).

Табл. 4. Типы сигналов, получаемых в результате применения различных схем их анализа при использовании нескольких форм преобразований на основе традиционного и вращаемого преобразований Фурье

Схема преобразования	Временнáя область α = 0	Область ВПФ 0 <  α <  π /2	Частотная область α = π /2
Вращаемое преобразование Фурье (ВПФ)	Непрерывный	Непрерывный	Непрерывный (ПФ)
Ряд ВПФ (Р_ВПФ)	Непрерывный, периодический	Дискретный, апериодический	Дискретный, апериодический (РФ)
Вращаемое преобразование Фурье дискретного времени (ВПФ_ДВ)	Дискретный, апериодический	То же	Непрерывный, периодический (ПФ_ДВ)
Дискретное ВПФ	Дискретный, периодический	Дискретный	Дискретный, периодический (ДПФ)

ЗАКЛЮЧЕНИЕ

Исходя из проведенного анализа, может быть отмечен ряд положений.

• •    Ряды вращаемого преобразования Фурье (Р_ВПФ) являются обобщением традиционных рядов Фурье; это обобщение построено на основе модифицированной формы ПФ, называемой вращаемым преобразованием Фурье.

• •    Коэффициенты разложения в такой ряд (в ряд вида Р_ВПФ) являются величинами отсчетов ВПФ.

• •    Отсчеты у огибающей коэффициентов Р_ВПФ становятся все более тесно расположенными по мере того как возрастает общий интервал Т вычисления этих коэффициентов. Когда интервал вычисления приближается к бесконечности, Р_ВПФ сходится к вращаемому преобразованию Фурье.

• •    Вращаемое преобразование дискретного времени (ВПФ_ДВ) является обобщением традиционного ПФ_ДВ и может быть получено дуальным разложением Р_ВПФ. Дискретное ВПФ (Д_ВПФ) может обеспечить метод для вычисления вращаемого преобразования Фурье для дискретных сигналов. С помощью алгоритма ВПФ_ДВ может быть реализован анализ дискретных сигналов на основе метода ВПФ.