Методы и средства управления характеристиками активных опор

Самарский государственный аэрокосмический университет

В работе рассмотрены методы и средства управления динамическими характеристиками активных опор роторных и стендовых систем с помощью регуляторов расхода. Рассмотрены случаи работы опор с газовой и жидкостной пленкой для различных режимов течения рабочей среды. Исследовано влияние параметров систем управления на динамические характеристики опор различного назначения. Показан метод выбора оптимального регулятора для активной опоры, работающей при заданном виде возбуждения.

Опорные узлы современных технических систем в силу повышающихся тактикотехнических требований нередко выполняются с использованием устройств активного типа с регулируемыми параметрами. В качестве управляющих элементов в активных опорах с внешним нагнетанием смазки, например, в гидро- и газостатических подшипниках и подпятниках, пневмогидростатичес-киих опорах (ПГСО), гидродинамических

Рис. 1. Типы регуляторов расхода для опор с внешним нагнетанием смазки а- регулятор постоянного расхода; б- интегрирующий регулятор; в- дифференциальный регулятор: г- регулятор с дополнительной механической связью демпферах, могут быть использованы регуляторы расхода различных типов (рис.1).

Регулятор расхода в таких устройствах в общем случае представляет собой гидравлическое сопротивление, величина которого изменяется в зависимости от давления на входе P _вх и в рабочей камере Р_К опоры. Они достаточно просто компонуются в опорах и обеспечивают существенное изменение их динамических характеристик. Регуляторы устанавливаются на входе в опоры и имеют активные связи пневмогидравлического и механического типа. Однако применение того или иного регулятора обуславливается необходимостью обеспечения заданного закона регулирования. Таким образом в процессе проектирования активных опор для выбора типа и параметров регуляторов расхода необходимо знать их законы регулирования. Активные связи в опорных узлах формируют дополнительные усилия, воздействующие на подвижную массу и зависящие от значений входных и выходных координат.

Использование положений теории релаксационного демпфирования позволило получить динамическую реакцию опорной системы в виде [1]

<    (S ) = C

T 1 S + 1 + W₂(S ) - W₄(S ) T 2 S + 1 - W 1 (S ) + W₃(S )

W1(S)-W4(S) - передаточные функции дополнительных каналов взаимодействия меж ду входной координатой и давлением в рабочей камере опоры;

W 1 (S) = 1^ ; W 2 ( S) = ^{Y 1 W} 1 ^M ;

^b 2 - b i ^ai - a ^

W 3 (S ) = ^Y W ;W₄(S) = ^Y W^M ' b ₂ - b ₁ a ₁ - a ₂

В каждом из каналов осуществляется преобразование координаты перемещения подвижной массы в ход элемента исполнительного устройства регулятора, которое далее преобразуется в изменение расхода рабочего тела. Преобразовательное устройство может быть механическим с передаточными функциями W_1M(S), W_2M(S) или пневмогидро-механическим W_1n(S), W_2n(S).

В зависимости от формы гидравлического тракта регулятора величины у могут быть как постоянными величинами (для золотника и регулятора сопло-заслонка) или функциями от S .

Введение дополнительных связей в опорах оказывает влияние на динамическую реакцию газового слоя и на резонансные характеристики системы. Закономерности этого влияния могут быть выявлены после опре-

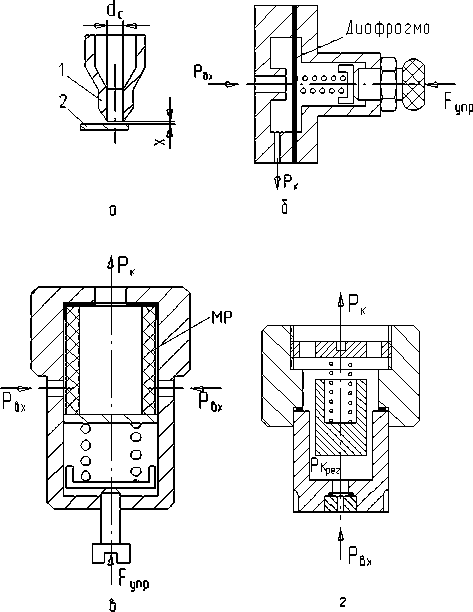
Рис. 2. Схемы регуляторов расхода а- регулятор сопло -заслонка;

б- мембранный регулятор; в- регулятор расхода из МР; г- регулятор гидростатического типа

деления передаточных функций элементов активных устройств и при учете их взаимодействия с другими структурными составляющими опорных узлов. Далее покажем это.

Сопло с дроссельной заслонкой

Регулятор расхода сопло-заслонка, имеющее сравнительно простую конструкцию (рис.2,а), широко используется в устройствах гидропневмоавтоматики. Оно состоит из сопла 1 и заслонки 2. Параметром регулирования является зазор х между соплом и заслонкой, изменяющейся при перемещении заслонки. Эффективное регулирование сопротивления регулятора сопло-заслонки возможно лишь при малых зазорах х между заслонкой и торцом сопла [2]. Обычно величина х не превышает 0,25 dC , так как при х=0,25 dC площадь сопла становится равной площади щелевого дросселя пdCх. Однако, на практике заслонка оказывает дросселирующее действие при значениях

х = (1,4 - 1,6) dC-

[3]. Расчет

дросселя состоит в определении его расходной характеристики. Для жидкости расход через дроссель рассматривают в виде м = oFj2(P„ - PK) р а - коэффициент расхода через,питающее 6Гверстие находится экспериментально (обычно а =0,62„.0,82 ); F площадь дросселя , равная минимальной из площадей пd(х и ndC2/4; р- плотность жидкости.

В работе [2] отмечено, что для газа при малых открытиях сопло-заслонка часто работает как ламинарный, а при больших - как турбулентный дроссель. Расходные характеристики дросселя для этого случая определяются по зависимостям для сверхкритического истечения газа

—

( к - 1) gRT

2         к + 1

в ^к - в ~

Для докритического истечения

M = o F _dp P _S x

к + 1

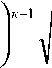
2 к

( к + 1) gRT

где к- показатель адиабаты; R - газовая посто- янная; g - ускорение свободного падения; Т -абсолютная температура ; в = Р^./ Р в- .

Значение коэффициента расхода определяется по экспериментальным данным, приведенным в работах [2,3]. Для этого предварительно находится вспомогательная величина

~ = f (Re) = Re

Д

Р_вЛ оЛ

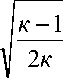
gRT

2        к + 1

в ^к - в ~

по которой отыскивается коэффициент расхода а [2].

Сопло-заслонка является усилителем с коэффициентом усиления для жидкости

UM1           I-------------- к = , = andc Д? - Рк ) р

В случае пневмогидравлической связи между опорой и регулятором его подвижный элемент снабжается упругим элементом с жесткостью Сп. При этом передаточная функция W1n отыскивается из уравнения равновесия всех сил, действующих на заслонку, m, S 2 Ox - OP + Сп Ох = 0.

Сила, действующая на заслонку со стороны сопла равна Р=Р 1 +Р₂, где Р 1 - реактивная сила, возникающая при попадании потока на заслонку и растекании его по поверхности заслонки при повороте на угол п /2; Р₂-сила статического давления, действующая на торец сопла и заслонку. Она определяется по формуле [3]

а для газа дМ      , „ /   2к к = —— = andrPm ,------- де      C “V (к -1)gRT

2        к + 1

в ^к — в ”

В приборах пневмогидроавтоматики заслонкой управляет маломощный чувствительный элемент. В активных опорах заслонка регулятора связана с перемещениями подвижного элемента опоры механически или пнев-могидравлически.В общем случае связь механического типа (рис.1,г) имеет передаточную функцию вида

O x =       С 1 + dS

8 1 ” m _x S ² + dS + C 1 + С ₂ ^,

где m 1 - масса заслонки (подвижного органа регулятора); С 1 , С₂ - жесткости, а d - демпфирование элементов связи.

Массой заслонки обычно можно пренебречь и в результате получаем передаточную функцию дополнительной активной связи механического типа, вносимой регулятором сопло-заслонка,

W ₂( S ) = k_P

1 + T P S

1 + T 2 _PS ’

+

где P

k C 1

( a 1 - a ₂)(C 1 + C ₂)

- коэффициент

4М ²

^{n d}c ^р с

+ * d C ⁽ ? 1 - ? 2 ) +

2П J Prdr - пР Гd^-dC dc             1          J

где р_С - плотность рабочей среды на срезе

сопла, d _н - диаметр торца, P r - текущее значение давления между торцом сопла и заслонкой, г- текущий радиус.

Сила давления на торце сопла J Р r rdr определяется с помощью экспериментальных d н - d_C, данных. Если величина---2---мала, то си

ловую характеристику дросселя типа сопло -заслонка, т.е. зависимость силы Р от зазора -, с достаточной точностью можно определить по приближенным зависимостям [2].

Подставляя в уравнение (7) приращение

ЯР = дР .

силы Р в виде ^{О Р} др ^{8 Р} 1 , получаем пере

даточную функцию регулятора типа сопло -заслонка

О _ д Р/ д Р 1 О Р 1 = ( b 2 - b 1 ) C п ^,

d усиления; T p = с и T 2p

d

C + C₂

- постоян

ные времени регулятора.

где С_п - жесткость упругого элемента заслонки.

Массой т1 заслонки можно пренебречь и тогда передаточная функция пневмогидравлической активной связи, вносимой соплом - заслонкой, имеет вид

W 1

k = k ^дР/ дР 1

P    ( b 2 — b) C_n

Следует заметить, что для регулятора расхода этого типа передаточная функция W1(S) вследствие наличия диссипативных сил в зазоре и упругом элементе в действительности близка к передаточной функции апе риодического звена

W i ( S ) =

k _P

.

T P S + 1

Золотниковый регулятор расхода

Золотниковые регуляторы значительно реже, чем сопло - заслонка, используются в пневматических устройствах. Они выполняются с малыми зазорами между втулкой и золотником и при работе на недостаточно очищенном воздухе или без смазки (вследствие трения и износа рабочих поверхностей) имеют пониженную чувствительность, нестабильны, возможны отказы в работе. Золотники могут иметь коническую или цилиндрическую (рис.1, а,б) дросселирующую щель и реализуют закон управления вида

W i ( S ) =

k _P

.

T P S + 1

Мембранный регулятор

В работе [4] предложено для повышения жесткости гидростатических опор использовать мембранный регулятор расхода (рис.2,б), представляющий собой щелевое сопротивление, величина которого изменяется при перемещении мембраны. Передаточная функция W/S) этого регулятора при наличии потока несжимаемой жидкости в трактах получена в виде

W i ( S ) =

T p S + 1     k

T 4 P S ² + T ₂ P S + 1 P .

Использование его в газостатических опорах требует уточнения вида W1(S) . Это связано со сжимаемостью газа. Учет динамических эффектов при сдавливании газа в рабочей щели оказывает существенное влияние на динамическую реакцию газового слоя, и, следовательно, на закон управления регулятора W1(S) .

Уравнение равновесия сил, действующих на мембрану m1, в приращениях имеет вид m1 S 2Sx + CMSx + SW = fSPK, (1) где 8W = Cдин (S)8х - приращение динамической реакции сдавливаемой газовой пленки в зазоре, См - жесткость мембраны, f. = nr2; r1- внутренний радиус щели.

Для отыскания W _{1 n} = 8 x, S P K необходимо найти величину § W . Для этого примем следующие допущения.

• 1.    Величина зазора х много меньше линейных размеров пластины и мембраны;

• 2.    Поток газа в рабочей щели считается ламинарным, что предполагает малые числа Re и параболический профиль скоростей в зазоре;

• 3. В любой точке потока выполняется

  соотношение

  
  

• 4.    Приращения § _х и 5 P K малы по сравнению со статическими х о и P K ₀ соответственно.

Р

= const л n             ^;

Воспользуемся результатами работы [5], где решено уравнение Рейнольдса для кольцевого упорного подпятника. Сила, действующая на сжимаемые пластины, равна

S W ( t ) = п ( r ₂ ² - r² ) J S P ( t , r ) dr r

где r ₁ = r ₁ / r ₂ ; r = r Ir ₂ ; r ₂ - наружный радиус щели. Применяя к (2) преобразование Лапласа временной функции

SW (S) = J SW (t) e - stdt, получаем выражение для динамической реакции газовой пленки в виде суммы бесконечного ряда

Проведенные исследования показывают его быструю сходимость. Поэтому возможно приближенное равенство с-(5) “ i+Sk ’       <3> где b = 48дг4(1 + в)(1 - r)2 ^ = п1 nx0Pkо пх03           ’ C 12^r22(1 - r)2"

Подставляя выражение (3) в уравнение равновесия (1), получаем передаточную функцию пневматической связи постоянные времени регулятора.

Видно, что передаточная функция дополнительной связи, обеспечиваемая мембранным регулятором, имеет высокий порядок, что затрудняет ее исследование. Однако, в области низких частот, характерных для работы опорных узлов, можно пренебречь членами высших порядков. В этом случае закон управления мембранного регулятора имеет вид

W 1 ( S ) = k P

T _p s + 1

T _{2 P} S + 1 .

w =

W 1П

8 х

ЗРк

fin miS Л + CM n + Ь ,

Необходимо добавить, что это упрощение не распространяется на устойчивость опоры.

где n 1 = 1 + S / to _C

Для отыскивания закона управления ре-

W 1 ^{( 5} ) = , _ , ^W 1л найдем величи-гулятора          b ² b ¹

ну у ₁ ( S ) . Расход газа в сечении радиусом r₂ для рабочей щели определяется в динамике как

М = М„ - S ( p v ) ,

где v = п(r2 - r23)х. Из выражения (4) полу- чаем, что дM  дM  й е _

Y 1 ( S )                  5 1 + 5 2 S ,    (5)

д и    д х

„    дM   „           2    2 х где 51 =      5 = -Рп(r1 - r2 ) .

дх

Это позволяет отыскать функцию W/S) в виде

W ( s ) = kP —T3 pS + T1 pS +1— PT6 PS3 + T4PS2 + T2 PS +1 ’ f5

где k P ⁼ ( b ₂

- коэффициент усиления ^Ь 1 ) C M

-

регулятора;

Регулятор расхода из МР

Пористый материал МР(металлорезина) может быть использован в качестве упругого и дросселирующего элемента регуляторов расхода, изменяющего свою пористость при изменении давления в камере или нагрузки, приложенной к элементу из МР. Конструкция упругого дросселя из МР показана на рис.2,в. Параметр регулирования - перемещение основания х. Течение газа только радиальное. Одним торцом упругая втулка крепится к основанию, другой - заглушен. По дросселирующим характеристикам регулятор расхода с МР может быть подобен мембранному регулятору, т.е. щели и заслонке с зазором И_э. Для последнего получено выражение для динамической реакции пленки (3), которое может быть использовано для расчета динамической реакции слоя в МР. Для этого необходимо отыскать зазор И_э щелевого дросселя - аналога МР, величина которого определяется из условия равенства гидродинамических сопротивлений МР и дросселирующей щели, т.е. R_MP ( х ) = R ^ ( h _э ) . При этом должны выполняться равенства R_MP ( х ₀) = R ^ ( h _{э 0}) и

T

T IP

T

1 3P

Ь

+

®C  CM e       ’ T4 P           ’ T6 P

51®C

=—+

5 1 ’

m

^CM ^ C

-

Р R . )

§ h _э

)

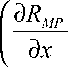
йхо. Отсюда дRMP ^ дх

5 h _э =

В соответствии с (3) и (6) получаем выражение для динамической реакции

C _дмн

V

Sr W ( 5 ) = — "^V     5P_K

K

^d R Щ

^d h » J о

bS

1 + 5 > C ’ ⁽⁷⁾

, fi 5 )

fi 1 + tor

VCJ f              ,

C mp Ь + — + b5

tor

V C ^J

ПГСО как регулятор расхода

1           KP K KP пр и выражения для динамической реакции слоя

где С_мр - жесткость втулки из MP.

С учетом выражений (5),(6),(7) получаем передаточную функцию дополнительной активной связи, обеспечиваемой регулятором расхода с MP, в виде:

,   _ F8PKP _ п 1 + T1P— _ динр = ^x _ CP 1 + t 5 . При этом

8 M u(S ) =

^ d n ^ Щ ^P _KP ^{- P}K

24 H gRT   x ²

где

kP

W i ( — ) = k p

T 3 _P 5 ² + T 1 _P 5 + 1

T 6 _P 5 ³ + T 4 _P 5 ² + T 2 _P 5 + 1 ’

W (S) = — =---------2--------- п v ’ 5p m 7

^0P K —П 2 S² + CT _X p S + C p - С пр ^;

F KP

(R Rp^ /R^ )    №,

V dx / dh , J , C „P ( 6 , - 6 , )’

W 2 (S ) =

k П 2

T = — + — T = ¹1P         ⁺ p ’^J 2 P

® C £ 1

^{d R}MP /^щ

B

V

dx / dh

, c

' , J 0 ^MP

6        1;

— + —

aC

ml- n 2 S ² + HS + C p - С пр

F K

T = ^2 T =

T 3 P _e      , T 4 P

^1® C

mm f, 6 P = m C

C MP       ^Ш С ^С МР

где

П 2 = 1 + T 2p S , B=( 6 2 - 6 , )’ H = ( CT , P - C np T 2 P ) .

Полученное выражение для области низких частот может быть упрощено до вида

Для определения гидродинамического сопротивления втулки из MP воспользуемся зависимостями, полученными в работе[6]. Для ламинарного потока через материал MP расход равен

W ₂( 5 ) = k _P

1 + B ₁ 5

1 + Н ₁ 5 ’

М = 4ж , L

п ³ а „ _р А Р р

153 ^ (1 - П )² ^ln A r A r    r ,

к = ^k н = т ^kP р         ’ ^B 1    ^T 2Р

^CP ^{- C}np

где

Н 1 =

с т р! 1Р

-С

ПР^ 2Р

С -С

Р п>Пр

AP = P™ - рк,Ar = r2 - r1, dnp - диаметр где проволоки, П- пористость материала, для газа р = Рср /RT

Для турбулентного режима течения через втулку из MP

A P 153(1 - и)² r , r₂ = ц  ln— M +

A r 4 n Lr₁n d_nm р A r r ,

+    1’⁴²(1 - и) r   M 2

8 ^{n 2} L² r; и¹ d „, r 2 р

Возможность широкого изменения параметров регулятора k_p, B 1 и Н 1 и наличие отработанной методики расчета делает регулятор этого типа весьма удобным для использования в гидрогазостатических опорах.

На рис.3-4 показаны амплитудно-частотные характеристики опор при различных значениях параметров регуляторов расхода k_P , T _{X p} , T_{2 P} . Их анализ позволяет заключить, что использование дросселей типа «сопло-заслонка» и золотника с коэффициентом усиления к_р < 0 уменьшает, а с k P > 0 - увеличива-

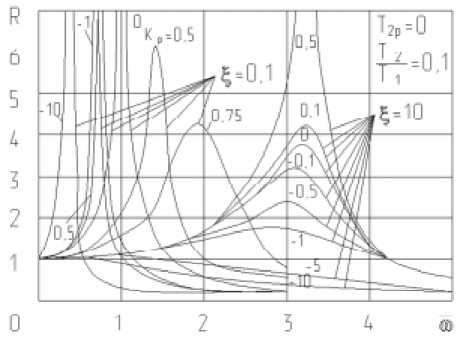
Рис. 3. АЧХ опоры с регулятором типа сопло -заслонка ет резонансную частоту. Влияние параметров регулятора на величину коэффициента усиления вибрации на резонансе зависит от значений параметра ^ = T1to0 (рис. 3).

Результаты расчетов амплитудно-частотных характеристик опор с мембранным, гидростатическим регулятором расхода и из материала МР приведены на рис.4. Влияние параметров k_P , T_{2 P} на АЧХ опоры аналогично результатам, полученным для сопла с дроссельной заслонкой и золотником. Увеличение постоянной времени Т_1Р с отрицательным коэффициентом усиления снижает резонансные частоты опоры, для которой ^> 10. При

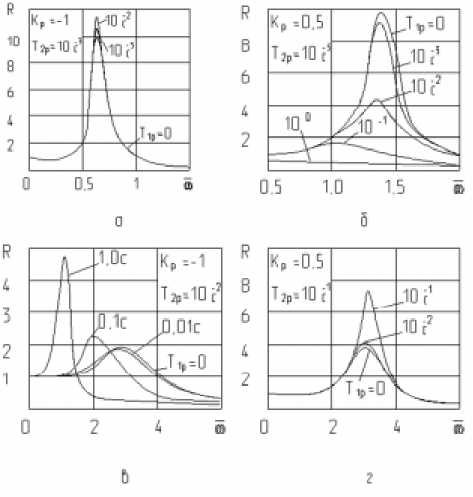
Рис. 4. АЧХ опор с регуляторами мембранного, гидростатического типа и из МР а, б - £ = 10; в, г - £ =0,1

этом уменьшается коэффициент усиления на резонансе. Для опоры с ^< 1 изменение Т_1Р в пределах, соответствующих устойчивым режимам работы, или практически не влияет на АЧХ системы, или приводит к незначительному увеличению резонансного пика. Использование регуляторов расхода с k_p > 0 приводит к обратным результатам.

Выбор оптимального регулятора

Повышение качества работы активных систем невозможно без выбора схемы и структуры регулятора и определения его оптимальных параметров. Для синтеза опоры, оптимальной по динамическим характеристикам, используется метод оптимальной фильтрации Винера [7]. Процедура оптимизации заключается в отыскании передаточной функции к_опт(8) оптимальной опорной системы, а по ней - передаточной функции регулятора расхода. Знание законов управления, реализуемых различными регуляторами, позволяет преодолеть трудности, связанные с реализацией передаточных функций в конкретную физическую систему.

Для составления интегрального уравнения Винера-Хопфа и получения к_oпт(S) воспользуемся критериальными функциями, включающими квадратичные значения (среднеквадратичные - для случайных процессов; интегральные квадратичные - для детерминированных) относительного перемещения x и ускорения на выходе Sx ₂ ,

F = e [ x ² ] + p E ( s ² x₂ ) ²

или

F = E [ ( S² X 2 )² ] + p E [ x ² ]        (8)

• -    для случайных процессов;

F = Jx + p JS ² x₂ или F = JS ² x₂ + p Jx (9) -для детерминированных процессов, где р - неопределенный множитель Лагранжа.

Критерии (8), (9) удобны для аналитических расчетов и применяются для выбора структуры и параметров опорной системы.

Решение для оптимальной синтезированной функции к_оnт(S) получено вариационными методами в работе [7] и имеет вид

^Ко„т ^{( S} ) =

[ Г (S )/ Д^— ( S ) ] Д⁺ (S)

где Г (S) = 2 п Ф(S) / S⁴ - преобразование Фурье для взаимно-корреляционной функции входа и выхода;

1      )

S 4 + pj Ф( S)

Д (S) = Д⁺ (S) -Д (S) = 2 П

• -    преобразование Фурье для корреляционной

  функции входа;

  
  

+^

Ф( S) = J e^vR( l )dt

—то спект

ральная плотность входного сигнала в операторной форме; R (т) - корреляционная функция входа.

Индексы «+» и «-» показывают, что полюса и нули функции находятся соответственно в левой и в правой полуплоскостях. Функция к_опт(8) и соответствующая структура оптимального регулятора зависят от характера входного возмущения.

В случае, когда вибрация основания представлена белым шумом, оптимальная функция к_опт(8) может быть реализована простейшей системой упругодемпфирующей подвески, представляющей параллельное включение демпфера и упругости. Для этого случая нет необходимости использовать активную систему.

Для узкополосного спектра с корреляционной функцией R ( t ) = D i e ^{— а} ' ^Т' и плотнос-

Di   а тью Ф(S) =        тг , где D. - дисперсия п d — S 1

возбуждения; а - коэффициент затухания корреляционной функции, функция K_onm(S) имеет вид

С у S² + C 1 S + C o ^Ко™ ⁽ ) s ² + 2 b a + 2 b² .

Здесь коэффициенты

,        2b( a + b)    , p

Co = 2 C,= 2bC. = a. + 2bs + 2b 2;b = Л уточнены по сравнению с полученными в работе [8].

Структуру и параметры оптимального регулятора расхода найдем после преобразований частотной передаточной функции опорного узла и выражения (10). В первом приближении в частотной характеристике передаточной функции можно пренебречь членом T2 S3, слабо влияющим на АЧХ опорного узла в области низких частот, и записать

K ( S ) =

^ o² ( t ; s + 1)

s ² [ 1 — W ( s ) ] + щпл + 1). ⁽¹¹⁾

Приравняв числители и знаменатели выражений (10) и (11), получаем, что оптимальная передаточная функция может быть реализована с регулятором, осуществляющим закон управления W(S) = kp / (1 + TPS) . Коэффициенты kp и Tp определяются через известные параметры вибрации и собственную частоту опоры kp

= 1 —

го а ²

2 b ² ( а ² + 2 a b + 2 b ²)^;

Т

1 p

Г 1

I ^b

— T p ^j

а + b b ( a ² + 2 a b + 2 b ²)

Таким образом, оптимальная работа опорной системы, служащей, например, для гашения вибрации узкополосного спектра, может быть осуществлена с помощью регуляторов расхода рабочего тела типа «сопло-заслонка» или золотникового типа.