Методы кодирования композиционных ДОЭ

В последнее время появились новые алгоритмы кодирования, предназначенные для быстрого (почти в масштабе реального времени) неитеративного расчета дифракционных оптических элементов (ДОЭ) или фазовых пространственных фильтров, которые реализуются с помощью фазовых пространственных модуляторов света (ПМС). Например, в [1] описан работающий на отражении ПМС фирмы Boulder Nonlinear Systems, Inc., состоящий из 120 x 128 электрически управляемых рабочих ячеек. Каждая ячейка заполнена нематическим жидким кристаллом. ПМС считывается линейно поляризованным зеленым лазерным пучком с длиной волны 532 нм. Скорость смены кадров равна 250 Гц.

Заданное число ячеек ПМС требует разработки специальных методов кодирования, отличных от классических методов цифровой голографии: методов Ломана, Ли, Кирка-Джонса и другие. В методах цифровой голографии каждый отсчет амплитуднофазовой функции, подлежащей кодированию, заменяется ячейкой KxK отсчетов цифровой голограммы.

В методах, ориентированных на ПМС, требуется каждый отсчет кодируемой амплитуднофазовой функции заменить на один отсчет фазовой функции. Другое ограничение для методов кодирования, ориентированных на применение ПМС, связано с режимом реального времени. Поэтому изображение, которое требуется сформировать с помощью ПМС, как правило, состоит из небольшого числа светлых пятен с минимальным дифракционным радиусом [1]. Это ограничение приводит к расчету композиционных ДОЭ, когда комплексную амплитуду пропускания ПМС находят как композицию (или суперпозицию) нескольких слагаемых:

NM f (%, У ) =Ц Cnm ^nm (%, У). (1) n =1 m=1

Например, для формирования набора световых пятен в плоскости пространственного спектра функции из уравнения (1) имеют вид:

^ nm ⁽ %, У ) = ^ex P ^{[ i} ( %u nm + У ^v nm ^)] , ⁽²⁾ где ( u_nm , v_nm ) – координаты центра светового пятна в Фурье-плоскости.

Для формирования контурных объектов, например букв, можно использовать метод расчета композиционных ДОЭ [2], в котором изображение состоит из набора отрезков.

Известны несколько методов кодирования композиционных ДОЭ, ориентированных на применение ПМС: метод наименьших расстояний [3, 4], метод диффузии ошибки [5, 6], метод псевдослу- чайного кодирования [7, 8] и их комбинации между собой [9, 10].

Метод наименьших расстояний (МНР) [3] по сути своей сходен с методом расчета киноформов [4] и состоит в замене модуля функции | f ( x,y )| на постоянное значение (при сохранении аргумента функции arg f ( x,y )):

I f% , у )|=1, ( %,у ) eQ ,                              (3)

где Q - форма апертуры ДОЭ. При этом модуль исходной функции f ( x,y ), определенной уравнением (1), может быть как больше, так и меньше единицы.

Этот метод кодирования дает наибольшую дифракционную эффективность е, но и наибольшую среднеквадратичную ошибку 8 при формировании заданного изображения.

Метод диффузии ошибки (МДО) [5,6] состоит в замене функции f ( x,y ) на фазовую функцию f ( x , y ) по правилу:

f ( % , у ) = exp [ i arg 0 ( % , у ) ] ,                       (4)

6(x,y)=:f(x,y)+p(x,y), p (%,у)=(q(%,y-а)+q(% -а,у))/2,

• q ⁽ % , у ) = 0 ⁽ % , у ) ^- 7 ⁽ % , у ),

где А - шаг дискретности в плоскости ДОЭ, ( %,у ) eQ .

Этот алгоритм, как и МНР, приводит к значительной эффективности (50–80%), но и к существенной ошибке (30–40%) при формировании изображения.

Метод псевдослучайного кодирования (ПСК) [7,8] состоит в замене функции f ( x,y ) на фазовую функцию по правилу:

f ( % , у ) = exp [ z arg ф ( % , у ) ] ,                       (5)

^ ( %,у )=arg ,/ ( %,у ) -sgn(S y ) ^ ( %,у ),

5 ( %,у ) = arccos(| / ( %,у )|),

SjG[—0,5, 0,5], где Sij – псевдослучайная величина, которая генерируется датчиком псевдослучайных чисел.

Этот алгоритм более адекватно учитывает амплитудную информацию функции f ( x,y ) и поэтому приводит к меньшей ошибке, но и меньшей дифракционной эффективности, в отличие от алгоритмов МНР и МДО.

В [9, 10] описаны алгоритмы кодирования ДОЭ, основанные на комбинации (смешении) алгоритмов МНР, МДО и ПСК. Цель комбинации этих алгоритмов в том, чтобы достичь уменьшения ошибки 8 (как в методе ПСК), но при этом чтобы эффективность е была существенной (как в методах МНР и МДО).

Методы кодирования композиционных ДОЭ основаны на уравнении (1), в котором комплексные коэффициенты C_nm определены неоднозначно, так как задается только интенсивность световых пятен в Фурье-плоскости | C_nm |², а их фазы arg C_nm могут быть произвольны. Поэтому при разном выборе фаз коэффициентов C_nm получаются разные значения эффективности е и ошибки 5. Причем, даже если задавать фазы C_nm с помощью датчика псевдослучайных чисел, результат будет меняться от реализации к реализации фаз коэффициентов.

Для того чтобы эффективность е и ошибка 5 менялись в широких пределах для одной и той же реализации фаз коэффициентов C nm в [9, 10], предложено ввести в схему алгоритма параметр у. Этот параметр управляет степенью смешения алгоритмов МНР, МДО и ПСК в комбинациях МНР–ПСК и МДО–ПСК.

Из уравнения (1) следует, что модуль функции f ( x,y ), если не сделана операция нормировки, может принимать значения от нуля до бесконечности. Но, как следует из (5), метод ПСК применим, если f ( x,y )| < 1. Поэтому если нормировать кодируемую функцию f ( x,y ) таким образом, чтобы максимальное значение модуля было равно заданному значению параметра:

Y = max| fx,y )|, ( x,y ) eQ , то смешение алгоритмов будет заключаться в следующем: если 1 < | f ( x,y )| < у , то применяется алгоритм МНР или МДО, а если | f ( x,y )|<1, то применяется алгоритм ПСК.

Заметим, что в [1] рассмотрен метод частичного кодирования при неитеративном расчете ДОЭ, в котором также введен параметр 0<а<1, регулирующий тип кодирования нормированной на единицу комплексной функции f(x,y ): если | fx,y )| > а , то применялся метод киноформа [4] с выравниванием амплитуды | f ( x,y )|=1 и сохранением фазы arg f ( x,y ), если же f ( x,y )|< а , то амплитуда кодировалась с помощью смещения фазового скачка на п по плоскости ДОЭ в рамках субапертуры из K х K элементов. Введение параметра а в [11] позволило менять оба параметра, характеризующие качество расчета ДОЭ (эффективность е и ошибку 5) в широких пределах.

В данной работе предлагается модернизация метода частичного кодирования для расчета ДОЭ, ориентированного на применение ПМС.

1.    Метод частичного кодирования, ориентированный на применение ПМС

Метод применяется к нормированной комплексной амплитуде:

g ( x,y ) = f ( x,y )(max| f ( x,y )|)^–1,

\g(x.y)\^ ¹ .

Нормированная амплитудно-фазовая функция g(x,y) заменяется на фазовую функцию g~(x, y) по правилу:

~( x , у ) =

exp{i arg[g (x, у)]},      |g (x, у )| > а, exp{i arg[g(x,у)]+ ip}, |g(x,у)| < а.

где

[л , sgn( S j ) >  0,

^Ц    [ 0, sgn( S j ) <  0,

8_че[-0,5, 0,5] - псевдослучайная величина.

Алгоритм (6), (7) означает, что если модуль нормированной амплитуды, подлежащей кодированию, больше порогового значения а, то применяется метод киноформа [4], если же меньше а, то фазы в соседних точках меняются на п, то есть увеличивается рассеяние света в окрестности данной точки ДОЭ.

В отличие от метода ПСК, в котором рассеяние света в точках ДОЭ, в которых амплитуда меньше единицы, происходит дозированно, то есть обратно пропорционально амплитуде, в алгоритме (6), (7) рассеяние происходит одинаково во всех точках ДОЭ, в которых амплитуда меньше а .

На рис. 1а показана полутоновая фаза в диапазоне [0,2 п ] кодированного ДОЭ размером 128 x 128, а на рис. 1б показано распределение интенсивности в Фурье-плоскости в виде 5 x 5 световых пятен с минимальным дифракционным радиусом. Интенсивность света в этих пятнах при расчете выбиралась равной единице, то есть в уравнении (1) | C_nm |=1, а фазы выбирались псевдослучайными: arg C nm = S nm , S nm – генерировались датчиком псевдослучайных чисел.

Рис. 1. Полутоновая фаза кодированного ДОЭ (а) и распределение интенсивности в Фурье-плоскости (б).

На рис. 2 показаны графики зависимости дифракционной эффективности е (кривая 1) и среднеквадратичной ошибки 5 (кривая 2) от значения параметра а для того же случая, что показан на рис . 1, только реализации псевдослучайной величины S nm были различными. Из рисунка 2 видно, что наименьшая ошибка 5 =15% достигается при а =0,31 с эффективностью е =52%. А при а =0 достигается максимальная эффективность £ =85%, но ошибка возрастает до 5 =30%.

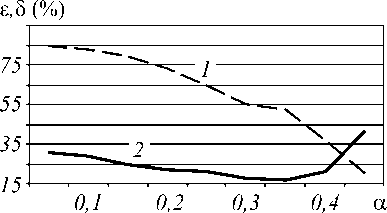
Рис. 2. Графики зависимости дифракционной эффективности s (кривая 1) и среднеквадратичной ошибки 5 (кривая 2) от значения параметра а .

Если рассматривать композиционные ДОЭ, формирующие объекты на заданном расстоянии z от плоскости ДОЭ, но состоящие из точек, а не линий, как в [2], в композиции (1) нужно использовать функции:

^V nm ( X , У ) = exP

■ л / 2

i    ( x

X z

+ У 2 )

X

^X exp [ z ⁽ xu nm + yv nm )]

где X - длина волны света, ( u_nm , v_nm ) - координаты центра светового пятна в Френель-плоскости z .

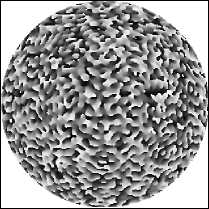
На рис. 3а показана полутоновая фаза в диапазоне [0,2п] кодированного ДОЭ размером 128 x 128 и радиуса 1 мм, а на рис. 3б показано распределение интенсивности на расстоянии z =100 мм от плоскости ДОЭ в виде 5 x 5 световых пятен с минимальным дифракционным радиусом. Коэффициенты C nm в уравнении (1) выбирались анологично ранее приведенному примеру. Как видно из рисунка, результаты получились несколько хуже (сравните рис. 1б и 3б), так как для функций вида (8) нужен меньший шаг дискретизации, чем для функций вида (2).

мм кольцо, состоящее из 40 световых пятен равной интенсивности (рис. 4в), а на расстоянии z 2 =500 мм треугольник, состоящий также из 40 световых пятен равной интенсивности (рис. 4д). Радиусы всех пятен равны минимальному дифракционному радиусу. На рис. 4б, г, е показаны распределения интенсивности в плоскостях z =50 мм, z =300 мм и z =700 мм. Для моделирования применялся быстрый алгоритм преобразования Френеля.

(а)

(б)

(а)                 (б)

Рис. 3. Полутоновая фаза кодированного ДОЭ (а) и распределение интенсивности на расстоянии z=100 мм от плоскости ДОЭ (б).

2. Композиционные ДОЭ для формирования нескольких изображений

Функции (8) можно использовать для расчета более сложных композиционных ДОЭ. Например, можно формировать различные изображения в плоскостях, расположенных на различных расстояниях от плоскости ДОЭ.

Тогда уравнение (1) примет вид:

PNpMp f (X, У) = 222 CnPm Vnm (X, У ) ,          (9)

p = 1 n = 1 m = 1

где

^V nm ^{( X} , У ) = ^exP i ^ ^{( X 2 +} У ^{2 ) X} _ Xz p           _

x exp [ ( xu

Заметим, что при этом значительно повышается количество слагаемых в композиции, что приводит к более равномерному распределению амплитуды | f ( x,y )|. В этом случае метод киноформа [4] может дать приемлемые результаты без специального кодирования.

На рис. 4 показан результат моделирования такого ДОЭ (256 x 256 отсчетов, радиус 1 мм) при освещении его плоской волной с длиной волны Х=633 нм. На рис. 4а показана полутоновая фаза некодиро-ванного ДОЭ, формирующего на расстоянии z 1 =100

(в)

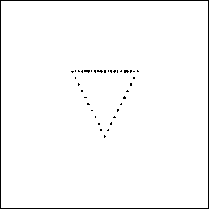
(г)

(д)                            (е)

Рис. 4. Полутоновая фаза некодированного ДОЭ (а) и распределения интенсивности на расстоянии z=50 мм (б), z=100 мм (в), z=300 мм (г), z=500 мм (д), z=700 мм (е) от плоскости ДОЭ.

Композиция (9) позволяет рассчитывать также ДОЭ, формирующие различные заданные изображения при освещении ДОЭ светом с различной длиной волны. В этом случае функции (10) будут выглядеть следующим образом:

^V nm ⁽ X , У ) = ^ex P

X exP[i(xu„Pm + yvpm )]

i П ( x ² + у ²) . ^X p z

Аналогично можно представить функции (2):

^{V p}m ⁽ X , У ) = ^ex P

i .     \ ^Xu nm ⁺ yv nm

^X p f

где f – фокусное расстояние сферической линзы.

Понятно, что можно еще усложнить ДОЭ, совместив уравнения (10) и (11) и варьируя как z , так и λ .

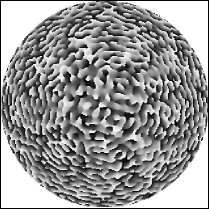
На рис. 5 показан результат моделирования композиционного ДОЭ (256 × 256 отсчетов, радиус 1 мм) для различных длин волн на одном и том же расстоянии z =100 мм. На рис. 5а показана полутоновая фаза некодированного ДОЭ, формирующего при длине волны λ 1 =488 нм крест, состоящий из тридцати шести световых пятен равной интенсивности (рис. 5в), а при длине волны λ 2 =633 нм кольцо, состоящее из девяноста световых пятен равной интенсивности (рис. 5д). На рис. 5б, г, е показаны распределения интенсивности для длин волн λ =244 нм, λ =560 нм и λ =705 нм.

(а)

(б)

(в)

(г)

(д)

(е)

Рис. 5. Полутоновая фаза некодированного ДОЭ (а) и распределения интенсивности на расстоянии z =100 мм от плоскости ДОЭ при длине световой волны λ =244 нм (б), λ =488 нм (в), λ =560 нм (г), λ =633 нм (д), λ =705 нм (е).

Заключение

В работе предложена модернизация метода частичного кодирования [11], ориентированная на расчет композиционных ДОЭ, предназначенных для реализации с помощью ПМС почти в реальном масштабе времени. Расчет фазы ДОЭ размерностью

128 × 128 точек, формирующего 5 × 5 светлых пятен, на компьютере Pentium II с тактовой частотой 400 МГц составляет 3 секунды. Результаты моделирования показали, что данный алгоритм не уступает по ошибке δ и в эффективности ε - известным алгоритмам кодирования подобного рода [3-10].

Показана возможность формирования различных заданных изображений на различных плоскостях, а также для различных длин волн с помощью композиционных ДОЭ.

Работа поддержана Российским фондом фундаментальных исследований (гранты 99-00-39012, 00-15-96114, 00-01-00031).