Методы количественного описания социальных последствий реализации проектов транспортной инфраструктуры
Автор: Карпович М.А.
Журнал: Вестник Воронежского государственного университета инженерных технологий @vestnik-vsuet
Рубрика: Экономика и управление
Статья в выпуске: 3 (57), 2013 года.
Бесплатный доступ
В статье рассмотрены методы количественной оценки позитивных и негативных последствий для населения строительства автомобильной дороги на прилегающей к населенному пункту территории. Население делится на группы с учетом географического, возрастного и гендерного распределения. Стоимостные параметры входят в целевую функцию в виде соотношения цена/отдача, а социальные, экологические факторы и риски – в виде безразмерных множителей и слагаемых.
Государственно-частное партнерство, оптимизация, функция социального влияния
Короткий адрес: https://sciup.org/14040084
IDR: 14040084 | УДК: 316.4.06
Текст научной статьи Методы количественного описания социальных последствий реализации проектов транспортной инфраструктуры
Реализация проектов транспортной инфраструктуры на принципах государственночастного партнерства требует перемещения ресурсов из частного сектора в государственный [1]. Для определения целесообразности такого перемещения необходимо сравнить предельную общественную выгоду с дополнительными (предельными) общественными издержками, которые связаны с производством каждой дополнительной единицы общественного товара. Реализация проекта является оправданной лишь при положительной разности выгод и издержек, а оптимизация методов выполнения проекта требует максимизации указанной разности. Поскольку как выгоды, так и издержки имеют весьма разнообразную форму (социально-экономическую, экологическую, медицинскую и др.) необходимо определение целевой функции (ЦФ) задачи, позволяющей учесть как положительные, так и отрицательные факторы строительства объекта транспортной инфраструктуры.
Поскольку параметры ЦФ имеют различную природу, их размерность также неодинакова. В то же время, постановка задачи оптимизации, в том числе и многокритериальной, требует формирование ЦФ, все слагаемые которой имеют одинаковую размерность. Эта задача в экономике решается различными
способами. В частности, возможно приведение всех параметров к всеобщему эквиваленту – деньгам. Однако при решении данной задачи получение денежного выражения для рисков , социальных и экологических результатов и потерь весьма сложно и представляет собой самостоятельную задачу, не имеющую однозначного решения [2]. Адекватным рассматриваемой задаче является альтернативный путь введения безразмерных характеристик объек -тов. При этом подходе стоимостные параметры входят в ЦФ в виде функции от соотношения цена/отдача, а социальные, экологические факторы и риски – в виде безразмерных множителей и (или) слагаемых. Именно такой подход и реализован в данной работе.
В частности, социальные последствия реализации проектов транспортной инфраструктуры приводят к увеличению подвижности населения, проживающего и/или работающего в зоне влияния данного объекта и, как следствие, увеличению доступности медицинских, образовательных, социальных, торговых и других услуг. С другой стороны, происходит также увеличение количества и улучшение качества доступных рабочих мест. В простейшем варианте количественное описание этих последствий может быть выполнено на основе данных о средней плотности населения в зоне влияния объекта дорожного хозяйства путем введения безразмерного социального коэффициента Ксоц:
К соц
_ Р об N мед N обр
ДД р рег мед обр
П П ПП торг спорт раб
Д Д ДД торг спорт раб
где роб, ррег - средняя плотность населения в зоне влияния объекта транспортной инфраструктуры и региона строительства соответственно; Nмед, Nмед - количество доступных населению медицинских учреждения до и после строительства объекта соответственно; индексы обр, торг, спорт, раб аналогичным образом описывают образовательные, торговые, спортивные объекты и количество рабочих мест соот-
ДП ветственно; величины З , З описываю среднюю зарплату на рабочих местах, доступных до и после введения объекта дорожного хозяйства.
Более точное описание социальных последствий строительства требует знания не только средней плотности населения, но и ее географического, возрастного и гендерного распределения. Связано это с тем, что различ ные группы населения имеют, во-первых, различные потребности. Так, например, потреб ность в медицинских учреждениях в нетрудоспособных возрастах значительно выше, чем в для жителей в работоспособном возрасте; потребность в образовательных и спортивных учреждения максимальна в младших возраст ных группах; роль размеров оплаты труда выше для мужской части населения. Кроме того, и зона влияния автодороги для лиц трудоспособного возраста больше, чем в нетрудоспособном. Учет этих особенностей различных групп населения, требующий значительных объемов статистической информации и использования более сложных алгоритмов целесообразен лишь при реализации масштабных проектов. При этом, поскольку затраты осуществляются, а прибыль получается за значительный промежуток времени необходимо их дисконтирование [3].
Количественно полезность участка авто дороги можно оценить, используя следующие параметры: ЦС - отношение дисконтированной стоимости строительства участка к прогнозируемой суммарной стоимости перевезенных грузов и арендных платежей за использование полосы отвода за вычетом дисконтированной выгоды, получаемой за счет использования отводимого участка в год окончании строительства:
ц - П ( 1 + «Л
Цс = и—---
Е с- В ' П ( 1 + а ) i = 1 i = 1
где Ц - стоимость строительства участка на момент сдачи дороги в эксплуатацию, N - глу- бина прогноза (при этом величина N не может превышать нормативного срока эксплуатации участка), индекс i нумерует год эксплуатации, а - прогнозируемый уровень инфляции, С - прогнозируемая годовая стоимость перевезенных грузов. Для платных автодорог вместо стоимости перевезенных грузов естественно учитывать прогнозируемую годовую плату за проезд П, собираемую на данном участке. В этом случае формула (2) модифицируется следующим образом:
Ц-П (1+а)
Ц с * "-------
Е П - В ' П( 1 + а )
i = 1
i = 1
Наличие транспортных коммуникаций и придорожной инфраструктуры положительно сказываются на занятости и доходах населения, тяготеющего к рассматриваемому участку. Однако этим социальный эффект автодороги не исчерпывается. Автодорога повышает общую мобильность населения и доступность для него рабочих мест, в том числе и не связанных непосредственно с дорожной инфраструктурой. Также повышаются доступность медицинских, образовательных услуг и возможности развития личности. Вследствие этого дорожная структура является одной из составных частей общественного договора. Формула (1) не учитывает численность и плотность населения, мобильность которого повышается, вследствие чего не в полной мере описывают социальные характеристики участков автодорог. Все это требует отдельного учета в ЦФ социальных характеристик участков автодорог.
Очевидно, что социальные эффекты сказываются тем сильней, чем ближе населенные пункты расположены к дороге. Они максимальны для населения, находящегося в зоне пешеходной доступности от участка дороги (по медицинским критериям - для населения в трудоспособном возрасте не более 3 км, для детей до 14 лет и лиц пенсионного возраста - не более 1 км). Вне зоны пешеходной доступности социальные эффекты затухают с ростом расстояния. Для расстояний, превышающих n кратное значение (например, n=5), социальным влиянием участка автодороги можно пренебречь. Простейшая функция социального влияния участка автодороги (ФСВ), удовлетворяющая указанным критериям, имеет вид:
f (x ) = 1,
x < x 0
n
x
fx n — 1 x 0 ( n — 1 ) ,
f (x )= 0,
—
x 0 < x < nx 0
x > nx 0
График зависимости функции социального влияния от расстояния х приведен на рисунке 1.
f(x)
ственного транспорта расстояние х0 определяется временем t0, необходимым для достижения участка автодороги. Для t0>2 ч. социальным влиянием участка для большинства населения можно пренебречь. Лишь небольшая часть населения, в основном активно использующая личный транспорт, повысит свою мобильность. При наличии общественного транспорта внутри населенных пунктов, находящихся в сфере влияния участка автодороги ФСВ можно описывать функцией вида
f (x ) = 1, x < x0
f (x ) = 2—a(x—x0) x0 < x
X0 ПХ0 x
Рисунок 1 - Функция социального влияния участка автодор оги
Наглядно степень социального влияния автодороги, соответствующая функции (4), изображена на рисунке 2. Степень черноты градиентной заливки пропорциональна значениям функции f ( x ) .
Параметр х0 совпадает с расстоянием пешеходной доступности лишь для населенных пунктов, не имеющих внутреннего общественного транспорта. При наличии обще-
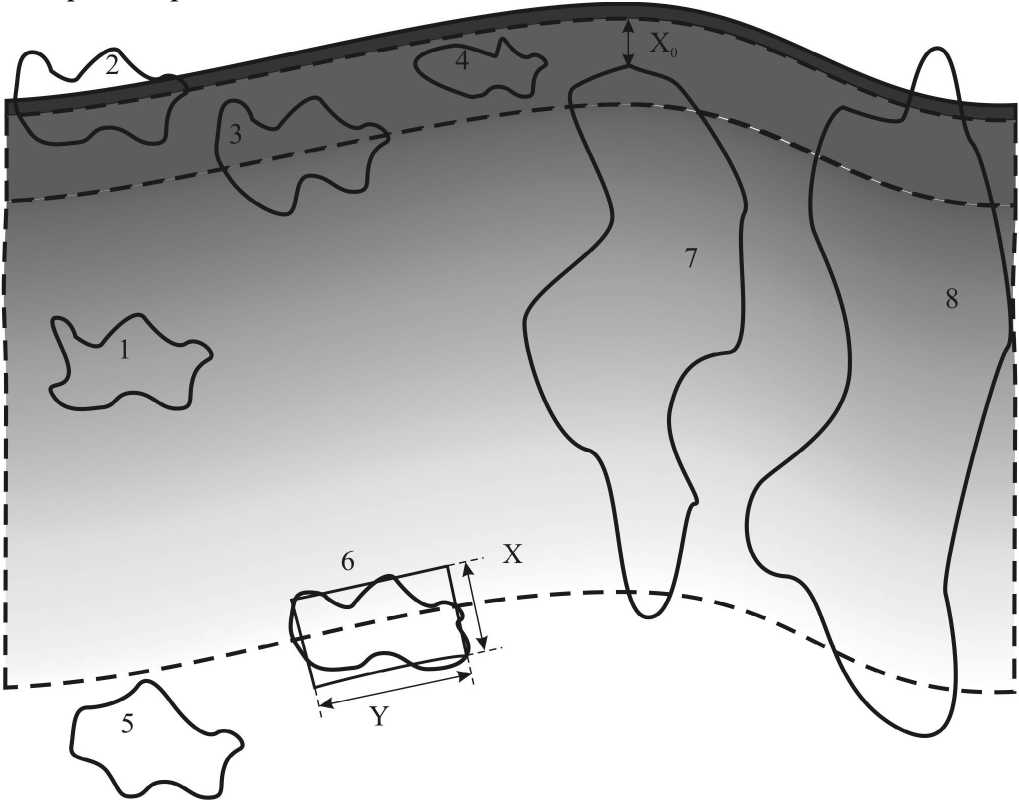
Рисунок 2 - Графическое представление степени социального влияния автодороги от расстояния х
Здесь параметр а обратно пропорционален средней скорости движения общественного транспорта с учетом времени его ожидания. С ростом ср едней скорости параметр а падает и область социального влияния автодороги растет. Так, например, при средней скорости V=10 км/ч, параметр а можно положить равным а=0,15 км-1. Тогда за 2 ч будет преодолеваться расстояние х2=40 км и, пренебрегая малым х0 по сравнению с х2, получим:
f ( x 2 ) = 2 — °-15 ' 40
64 .
Таким образом, в этом случае менее 2 % населения окажется в зоне влияния, превышающей х2.
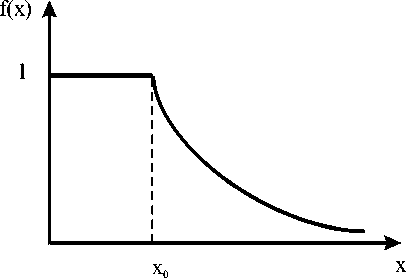
Рисунок 3 - Функция социального влияния участка автодороги при наличии маршрутов общественного транспорта
Функции (3) и (4) описывают социальное влияние автодороги на часть населения, не использующую личный транспорт. Для части населения, активно использующей личный транспорт, зона повышения мобильности значительно выше, чем зона пешеходной доступности и ФСВ медленнее спадает с ростом расстояния. При этом скорость уменьшения ФСВ обратна средней скорости личного транспорта на участке, соединяющем населенный пункт и автодорогу. Для этой части населения функция социального влияния является монотонной и, в простейшем случае, может быть представлена в виде:
.ft (x )= 2- “ (6)
График функции (6) представлен на рисунке (4). Полная ФСВ является суммой функций f ( x ) вида (3) или (4) и функций f 1 ( x ) с весами, равными долям населения, не пользующегося и активно использующего личный транспорт соответственно:
Кроме ФСВ, общая численность населения, повышающего мобильность (ЧН), а, следовательно, и целевая функция зависят также и от распределения плотности населения р p ( x , y ) в зоне влияния участка автодороги для расстояний x < n • x 0 . Здесь у - параллельная, х - перпендикулярная к оси дороги координата. В частности, для прямолинейных участков автодороги х и у совпадают с декартовыми координатами. В общем случае ЧН определяется интегрированием произведения ФСВ и плотности р p ( x , y ) по площади населенного пункта:
ЧН = JJ f ( x ) • р ( x , y ) dxdy , (8) S
Последовательный расчет ЧН по формуле (8) требует детальных демографических и топографических данных. На этапе обоснования инвестиций в большинстве случаев можно ограничиться усредненной моделью распределения населения. В этой модели вне пределов населенного пункта плотность населения считается равной нулю, а внутри поселения - постоянной. Топографически населенный пункт моделируется обобщенным прямоугольником с линейными размерами Х и У, минимальное расстояние от которого до автодороги равно Х0 (рисунок 2). В этом приближении интегрирование по продольной и поперечной координате в формуле (8) выполняются независимо:
ЧН = р0 J fполн (x)dxJdy = х 0 0 , х 0 + X
= р 0 Y J f полн ( x ) dx
X 0
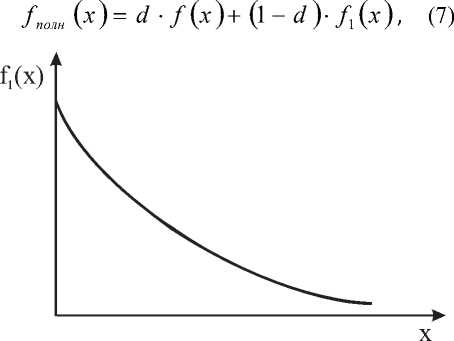
Рисунок 4 - Функция социального влияния участка автодороги для населения, активно использующего личный транспорт
р здесь r0 - средняя плотность населения в границах населенного пункта.
Ответ выражается через элементарную функцию, конкретный вид которой определяется соотношением между параметрами X, X0, x0 и видом ФСВ. Рассмотрим вначале населенные пункты, не имеющие маршрутов общественного транспорта, и население, не использующее личный транспорт.
Если все поселение находится в зоне пешеходной доступности участка автодороги (населенный пункт 4 на рисунке 2) , что математически сводится к справедливости неравенств X 0 < x 0 , X 0 + X < x 0 , значение подынтегральной функции равно единице на всем интервале интегрирования и, следовательно:
ЧН
X 0 + X X 0 + X
p0 Y j f (x)dx = p 0 Y j dx = p 0 YX = p 0 5 = N ,
X 0
X 0
здесь S – площадь населенного пункта, N – общая численность населения.
В тривиальном случае для поселения, целиком лежащего за пределами зоны влияния дороги (населенный пункт 5) на всем множестве интегрирования значение функции f (x) равно нулю, вследствие чего нулевое значение принимает и функция ЧН. Если весь населен- ный пункт находится в зоне влияния автодороги (X0 + X < n • x0), и часть поселения находится в зоне пешеходной доступности (X0 < x0) (населенный пункт 3), значение подынтегральной функции отлично от нуля на всем интервале интегрирования, и выражение (7) приобретает вид:
ЧН = Р 0 Y
x 0
j dx +
X 0
n - 1
X 0 + X ( j I n x 0 V
-
-
V x 0 у
dx
= Р 0 Y
x 0
X + n ( X 0 + X - x 0 ) - ( X 0 + X ) 2 - x 02
0 n - 1 2 x 0 ( n - 1 )
Если весь населенный пункт находится в зоне влияния автодороги ( X 0 + X < n • x 0 ) и отсутствует часть поселения, находящаяся в зоне пешеходной доступности ( X 0 > x 0 )
(населенный пункт 1), значения подынтеграль ной функции положительны и отличны от еди ницы на всем интервале интегрирования:
ЧН =
Р 0 Y n - 1
X 0 + X j x 0
(
n
V
—
x J
— dx =
x 0 у
p 0 Y n - 1
n(X0 + X - x0)-
(X0 + X )2 - x 0
p 0 Y ( X 0 + X - x 0 X2 n - X 0 - X - x 0 ) 2 ( n - 1 )
Если лишь часть населенного пункта находится в зоне влияния автодороги (X 0 + X > n • x 0), и отсутствует часть поселения, находящаяся в зоне пешеходной доступности (X 0 > x0) (населенный пункт 6), верхний предел интегрирования в выражении (8) опреде ляется максимальным расстоянием влияния ав тодороги, а нижний – минимальным расстояни ем от автодороги до поселения:
ЧН = pY ff n - — 1 dx = p 0 Y n -1 J I x 0J n -1
x 0 0
( х (nx0 )2 - x22 n (nx 0 - x 0)- "—---
V f 2 n + 1 ) p Yxo
p0YI nx0 - x0 -у I = ~2—12n - x0(n + 1)].
И, наконец, если лишь часть населенного пункт находится в зоне влияния автодороги
(X 0 + X > n • x 0), и имеется часть поселе- ния, находящаяся в
зоне пешеходной доступ-
ности ( X 0 < x 0 ) (населенные пункты 7 и 8), выражение для ЧН содержит слагаемые, отражающие вклад как зоны пешеходной доступности, так и остальной зоны влияния:
ЧН = p 0 Y
x 0
j dx
X 0
+--- n-1
nx 0
j x0
n -
V
x V г
— dx = p 0 Y x
x01 L
0-
„ n 2 x 0 1 /
X 0 +--- -■-x 0 ( n + 1 ) .
n - 1 2
n - 1
Поскольку значение параметра x 0 для различных групп населения является различным, эффективное значение ЧН определяется суммированием частных его значений для населения в трудоспособном и нетрудоспособном возрасте с весами, определяемыми долями населения каждого из возрастов в данной местности:
ЧН Э = ТР • ЧН ( x ТР ) + ( 1 - ТР ) • ЧН ( x НТР ) , (15)
где ТР – доля трудоспособного населения, ТР НТР x 0 , x 0 есть расстояния пешеходной доступности для лиц трудоспособного и нетрудоспособного возраста соответственно.
Рассмотрим теперь населенные пункты, имеющие маршруты общественного транспор- та. В этом случае расчет упрощается, так как параметр x 0 одинаков для всех групп населения, нет необходимости проводить суммирование (15) и формула (14) непосредственно дает окончательный ответ. Кроме того, поскольку функция (5), в отличие от (3), имеет x0
ЧН внутр = Р 0 Y J dx
X 0
лишь две функционально отличающиеся области, реальный расчет численности повышающего мобильность населения сводится к разбиению населенного пункта, находящегося внутри и вне зоны х 0 , и применению к каждой из областей следующих формул:
Р 0 Y ( x 0 - X 0 ) = Р 0 S внутр = N внутр (16)
и
X 0 ^ax 0 (a-ax 0 --aX 0 I
ЧН„ = Р 0 Y 12 - "dx = Р 0 Y -------) - (17)
x . a ln ( 2 )
здесь введено обозначение N внутр – численность населения данного пункта, проживающего в зоне x < x 0 , и использован табличный интеграл:
J 2 - axdx =-
2 - ax a In (2)
Так, например, для населенного пункта 4 на рисунке 2, целиком расположенного в зоне x < x0, расчет численности повышающего мобильность населения сводится к применению формулы (13); для населенных пунктов 1, 5, 6, целиком расположенных в зоне x > x 0, вычис- ление ЧН проводится по формуле (14); лишь для поселений 3, 7, 8 необходимо разбиение на части (x < x0 и x > x0 соответственно) и применению к каждой из них формул (12) и (15).
Проще всего расчет ЧН выполняется для части населения, активно использующего личный транспорт, что определяется простотой выражения (6). В этом случае нет необходимо- сти учитывать ни возрастную структуру населения, ни топографическое расположение населенного пункта. ЧН в любом случае определяется выражением:
x max afax 0 - ""ax 0 ,-t bx(a^X max 9 bx min I
ЧН = Р Y 2 - bx dx = Р Y 2 ■ 2 . = Р 0 Y ( 2 -- 2 2--- ) , (19)
0 x m. b *n ( 2 ) b *n ( 2 )
x ,x здесь min max – просто минимальное и максимальное расстояние от дороги до границ населенного пункта, отсчитываемое вдоль внутренних дорог и улиц.
Для участков автодорог, проходящих через населенные пункты и делящих их на части (населенные пункты 2 и 8 на рисунке 2), общую формулу (8) и ее частные случаи необходимо применять для каждой из частей независимо и результаты суммировать. При некоторых топографических схемах расположения участков автодорог (например, для окружных дорог в окрестности небольших населенных пунктов) могут возникнуть зоны перекрытия различных значении функции влияния ФСВ . Реально перекрытие означает доступность для населения различных участков дороги. Наиболее естественным поведением в этом случае будет использование участка с максимальной доступностью. Математически этот факт отражается учетом лишь максимального значения функции ФСВ и отбрасывания минимального значения ФСВ . Общий метод, основанный на применении формулы (8), позволяет без труда определить значение ЧН и в этих случаях.


