Методы наноплазмоники в угловой спектроскопии наноразмерных биологических объектов

В настоящее время наноплазмоника является современным быстро развивающимся направлением нанофизики [1–3]. Направление основано на возбуждении в наноструктуре объемных и поверхностных плазмонов – коллективных возбуждений, имеющих смешанный - механический и электромагнитный - характер. Наиболее перспективными для различных практических приложений являются поверхностные плазмоны [2–4], которые при определенных условиях возникают на границе раздела металл–воздух.

Возбуждение поверхностных плазмонов (ПП) на границе благородных металлов характеризуется наличием очень узкого резонанса, что позволяет использовать такое явление в диагностических целях. Схема Кречмана отличается тем, что металлический слой, на границе которого с воздухом возбуждается поверхностный плазмон, находится сразу после призмы, и он играет основную роль в формировании отраженного сигнала. Необходимым условием такого возбуждения являются отрицательные значения действительной части диэлектрической проницаемости. Эта схема представлена на рис. 1.

1.    Расчет основных характеристик поверхностных плазмонов

В качестве проводника было выбрано серебро, комплексная диэлектрическая проницаемость которого на длине волны X = 633 нм имеет отрицательную действительную часть Б2 =—18,2 + 0,5i• Такой металл, как золото, имеет на этой длине волны также большую отрицательную действительную часть и относительно небольшую мнимую часть. Следовательно, эти благородные металлы являются очень хорошими материалами для возбуждения ПП на их границе с воздухом. Сами ПП при распространении по поверхности металла затухают, поэтому имеют конечную длину пути. Последняя – одна из важных характеристик ПП. Сам процесс возбуждения ПП по схеме Кречмана приводит к появлению этих коллективных возбуждений, для которых дисперсионное уравнение имеет вид k 2 = Ч£2

^£ 1 ^+£ 2

Для действительной и мнимой частей параметра распространения можно получить следующие уравнения:

к = к' + i к", к = к о (n ' + i n"),

, го к о =- c к = к о (n ' + in"),

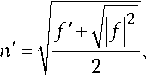
f =

I^|2

f

2 n' ’

+S 1 S₂ - i S 1 S 2

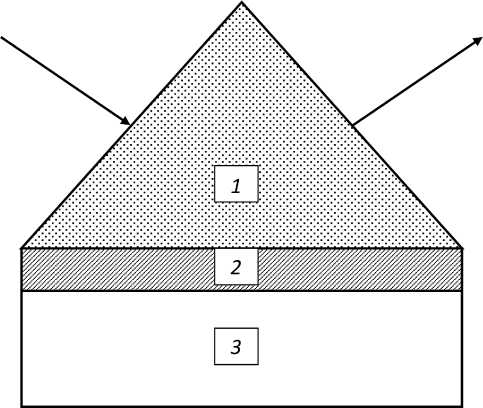
Рис. 1. Схема Кречмана для возбуждения поверхностных плазмонов: 1 – диэлектрическая призма; 2 – металлический слой; 3 – воздух

Fig. 1. Kretschman’s scheme for the excitation of surface plasmons: 1 – dielectric prism; 2 – metal layer; 3 – air

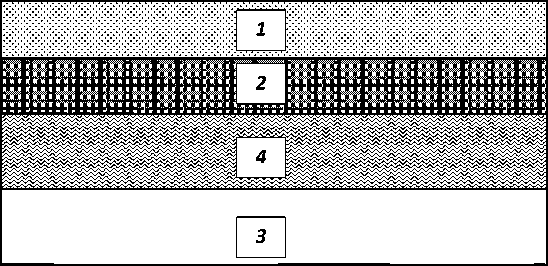
Рис. 2. Схема угловой спектроскопии биологического объекта (слой 4) с участием поверхностных плазмонов. Обозначения остальных слоев такие же, как на рис. 1

Fig. 2. Schematic of angular spectroscopy of a biological object (layer 4) with the participation of surface plasmons. The designations of the remaining layers are the same as in Fig. 1

Здесь ε ₁ = 1 – диэлектрическая проницаемость воздуха; ω – частота волны; c – скорость света.

Если сканировать оптическое излучение, падающее на поверхность призмы по схеме Кречмана, по углу падения, то в энергетическом спектре отражения появляется узкий резонансный минимум, характерный для возбуждения ПП на границе серебро–воздух. Такой пик служит точкой отсчета при анализе спектра углового отражения пленки с биоматериалом, нанесенным на серебро из воздуха.

2.    Результаты расчетов и обсуждение результатов

Когда наноразмерный слой биологического объекта помещается на поверхность проводника (см. рис. 2), этот резонансный пик смещается на определенную величину. Для различных образцов биологического материала этот сдвиг относитель- но контрольного значения уникален и, таким образом, служит индикатором этого вещества. Мы провели расчеты такого сдвига для ряда биологических объектов. Расчет проводился для энергетических спектров не только отражения, но также и пропускания. Анализировались эллипсометрические параметры, а также использовался падающий свет различной поляризации. На рис. 3 показан угловой спектр энергетического коэффициента отражения, полученный в результате нашего расчета по схеме рис. 2. В частности, для слоя серебра толщиной d = 0,05 мкм и нанослоя биологической ткани толщиной db = 0,03 мкм положение пика соответствует следующим углам: серебро θ1 = 40,65°, биоткань 62 = 43,5°, меланин 63 = 45,05°.

На рис. 4 показаны угловые спектры серебра и слоя воды. В этом случае минимум соответствует углу θ ₄ = 43°.

На приведенных рисунках наблюдаются очень узкие угловые пики, характерные для каждого

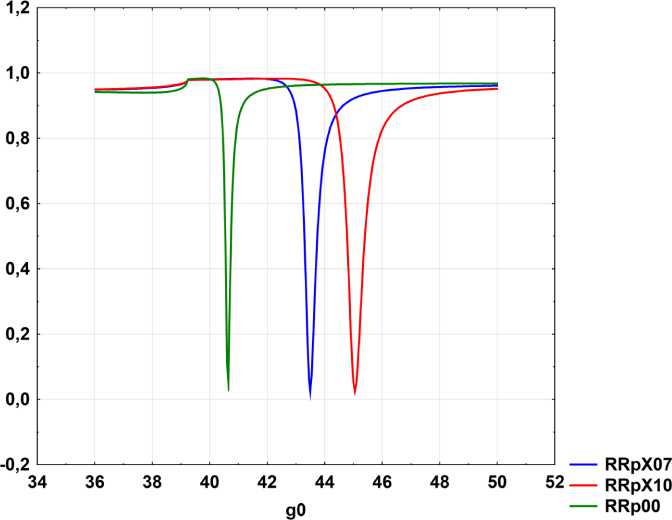
Рис. 3. Угловая зависимость энергетических коэффициентов отражения в следующих случаях: RRp00 – только металлический слой (рис. 1); RRpX07 – слой биологического объекта (ткани) на металлической поверхности (рис. 2); RRpX10 – это слой биологического объекта (меланина). Параметры расчета: толщина слоя серебра d = 0,05 мкм, толщина биологического объекта d_a = 0,03 мкм Fig. 3. Angular dependence of the energy reflection coefficients in the following cases: RRp00 - only the metal layer (Fig. 1); RRpX07 – a layer of a biological object (tissue) on a metal surface (Fig. 2); RRpX10 – a layer of a biological object (melanin). Calculation parameters: thickness of the silver layer d = 0,05 μm, thickness of the biological object d_a = 0,03 μm

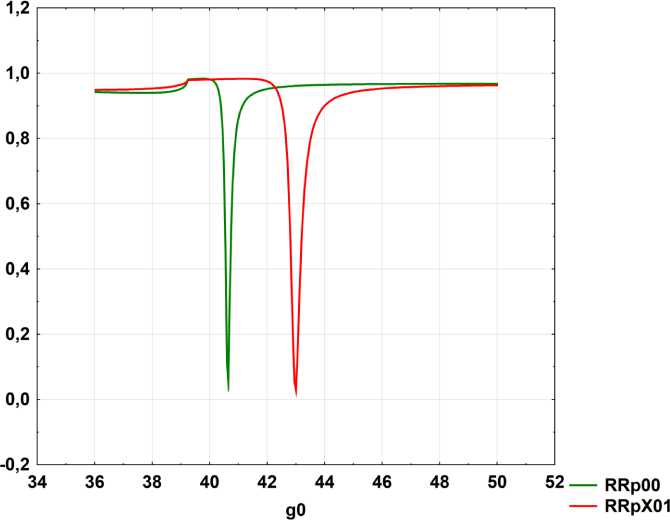
Рис. 4. Угловая зависимость энергетических коэффициентов отражения в следующих случаях: RRp00 – только металлический слой (рис. 1); RRpX01 – это слой воды на металлической поверхности (рис. 2). Параметры расчета: толщина слоя серебра d = 0,05 мкм, толщина биологического объекта d_a = 0,03 мкм

Fig. 4. Angular dependence of the energy reflection coefficients in the following cases: RRp00 – only the metal layer (Fig. 1); RRpX01 – a layer of water on a metal surface (Fig. 2). Calculation parameters: thickness of the silver layer d = 0,05 μm, thickness of the biological object da = 0,03 μm материала, угловые расстояния которых от главного пика, обусловленного возбуждением поверхностных плазмонов на границе металла, и представляют в данном методе количественную спектрометрическую информацию относительно конкретного вещества.

Следовательно, метод возбуждения поверхностных плазмонов на границе раздела воздух–серебро по схеме Кречмана позволяет проводить диагностику биологических объектов нанометрового масштаба.

Заключение

В работе представлены результаты расчетаугло-вых спектров отражения для слоя нанообъекта с применением методов наноплазмоники. Показана высокая чувствительность метода при диагностике биологических объектов наноразмерной толщины. Рассмотренный метод оперирует с очень узкими резонансами в угловых спектрах, что позволяет проводить идентификацию исследуемого биологического объекта с высокой степенью надежности, характерной для методов резонансной спектроскопии.