Методы оценивания импульсной характеристики системы OFDM в канале с памятью

В системах сотовой связи широкое применение получила технология ортогонального частотного мультиплексирования (OFDM) для эффективного использования отведенной полосы частот и борьбы с помехами при передаче полезной информации по радиоканалу[1]. Технология OFDM применяется в стандартах передачи данных LTE, LTE-А, будущих сетях поколения 5G, а также в сверхширокополосных сетях передачи данных.

Формирование OFDM-сигнала

Технология OFDM основана на формировании многочастотного сигнала, состоящего из множества поднесущих частот, отличающихся на величину выбранную из условия ортогональности сигналов поднесущих частотах, поднесущая частота. Для формирования сигнала OFDM поток последовательно передаваемых информационных символов разбивается на блоки, содержащие N символов. OFDM-сигнал представляет собой сумму поднесущих гармонических колебаний, каждая из которых модулируется своим подпотоком передаваемых символов с использованием квадратурной амплитудной модуляции (КАМ) или других видов модуляции.

Рассмотрим КАМ-16. Пусть на входе КАМ-модулятора наблюдается последовательность кодовых символов Затем четыре кодовых сим- вола преобразуется в – комплексное число, характеризующее одну из 16 сигнальных точек, где амплитуда и фаза        для i-го подне сущего колебания. Таким образом, если число ортогональных поднесущих равно N, то значения отсчетов комплексной огибающей OFDM-символа длительности Т запишутся в виде [1]:

w-i • 2тг

/=о

Т где

N – число ортогональных поднесущих.

Данная последовательность отсчетов получается с помощью операции обратного дискретного преобразования Фурье (ОДПФ). Совокупность отсчетов         последовательно во времени передается по каналу связи. При отсутствии временного рассеяния в месте приема для решения задачи оценки символа    достаточно было бы совершить прямое ДПФ и интегрирование совокупности отсчетов       В реальных каналах связи присутствует межсимвольная интерференция из-за ограниченности полосы частот и многолучевого распространения сигнала, что существенно искажает последовательность вследствие чего последующая операция ДПФ не позволяет выявить последовательность необходимой точностью. Можно утверждать, что на любой отсчет на приеме будет оказывать интерференционное воздействие каждый из М – 1 предшествующих отсчетов (М-память канала).

Каналы с межсимвольной интерференцией характеризуются памятью, которая определяется интервалом т временного рассеяния энергии передаваемого сигнала. Будем считать, что параметр М = — определяет длительность им-

М пульсной реакции канала, выраженная числом тактовых интервалов Δt.

Если импульсная характеристика определяется отсчетами ^ h_x... h_M__x, то на приемной стороне вектор отсчетов принимаемых символов в матричной форме запишется в виде:

z6 = u‘ • H* + w6,            (2)

где и4

»0

йх

ll

^Mo й_л ^N-l

– матрица от-

счетов огибающей передаваемого OFDM сим-

вола; H – диагонально-блочная матрица, состав-

ленная из отсчетов импульсной характеристики, W = [w₀,w_l,...,w_Ar+A/_₁] – вектор отсчетов случайного белого гауссовского шума (БГШ), k –

номер итерации в алгоритме оценивания.

Обозначим через H оценку импульсной характеристики канала H . Одним из вариантов обработки является применение алгоритма обработки сигналов в каналах с памятью – «прием «в целом» с поэлементным принятием решения» (ПЦППР), реализация которого подразумевает использование обратной связи по решению (ОСР) [2].

Для реализации алгоритма ПЦППР в месте приема необходимо знание отсчетов импульсной характеристики. Оценивание отсчетов импульсной характеристики можно реализовать как показано в [12] с использованием пилот-сигналов,

периодически повторяющихся между передаваемыми OFDM-символами, информационное содержание которых известно. Решение задачи при этом сводится к оценке отсчетов импульсной реакции из соотношения (2), в котором неизвестными теперь являются элементы матрицы H, а содержание вектора U известно на приеме.

Методы оценивания импульсной характеристики

Проблема оценивания импульсной характеристики канала связи занимает центральное место в ряду проблем построения системы приема со-

общений в реальных условиях и существующей помеховой обстановке. Рассмотрим возможные методы для оценки импульсной характеристики канала с памятью:

– метод наименьших квадратов [3];

– метод регуляризации[4].

При использовании метода наименьших квадратов задача состоит в том, чтобы выбрать такое значение оценки вектора H , при котором значение квадратичной формы оказывается минимальным:

J(H⁴) = |(Z⁴ -и*н‘)^г -R"'-^ -U*H⁴), (3)

где R ¹ – матрица весов (штрафов) размера MxM . Оптимальная оценка, которая минимизирует функционал (3), будет оценкой наименьших квадратов. Следовательно, оценки наименьших квадратов являются корнем уравнения

-^/HA=H1S=O .

()

Минимизация согласно (4) дает

H‘ =((Ut)r-R-1-Uirl-(Ui)r-R"l-Z4. (5)

Введем обозначения

p* =((UA')r R 1 -U^)"1.

Подставив P* в (5), получаем формулу для формирования оценки наименьших квадратов:

H4 =P4-(U4)4-R-’-Z4.

Предположим, что на каком-то интервале времени, когда были переданы следующие пилот-символы, произведено новое очередное измерение вектора Z:

zt+1 = UA+I • Hi+1 + WA+1.

Путем матричных преобразований получаем алгоритм вычисления оценок методом наименьших квадратов:

уЫ ₌ Ц1 ₊ pA₊l, ^4+1 у . _R-1 , ^₊1 _ _ut+lyi ^ .

Таким образом, новое значение оценки импульсной характеристики вычисляется с использованием оценки на предыдущем k -ом шаге. Также для оценки параметров канала связи можно использовать метод регуляризации. Идея метода регуляризации состоит в том, что оценка

импульсной характеристики рассчитывается по формуле:

н^ = ((1?/ -U^ + «I)-1 W -Z^,  (6)

где вводится Ct – параметр регуляризации; I – единичная матрица.

Если матрица весов R является единичной матрицей, тогда при a = 0 регуляризационные оценки совпадают с оценками метода наименьших квадратов. Значения U^A' в формулах (5)-(6) могут быть вычислены заранее до приема пилот-сигналов.

Для сравнения методов оценивания импульсной характеристики воспользуемся моделированием алгоритмов оценивания. Точность оценивания будем характеризовать среднеквадратической ошибкой, вычисленной при разных отношениях «сигнал/шум».

Моделирование алгоритмов оценивания импульсной характеристики

Моделирование проводилось для канала с аддитивным белым гауссовским шумом, памятью канала M = 4 и набором отсчетов импульсной реакции:

Ло = 2 + 3z; hx = —0,5 + 0,5z;

A2 =1 + 1,5z; Л3 = 1 + 3z.

Для сравнения методов оценки воспользуемся нахождением нормированного значения £ среднеквадратической ошибки (СКО) оценки импульсной характеристики hj . Нормированная среднеквадратическая ошибка £ рассчитывается по формуле e =CKO/ E , где

CKO = (/z0-/z0)2+(/z1-A1)2 +

+ ■•• + (^-1 -^/-i) ;

E = {h0Y +{hx}2 +... + (AM_1)2.

Соотношение мощностей сигнала и шума задавалось по формуле p_c /р_ош =E/a , где – дисперсия шума. Оценки импульсной характеристики для сравнения методов рассчитывались по формулам (5)-(6). Параметр регуляризации в (6) выбрался равным α = 0,01.

По известным пилот-символам, имеющимся в структуре группового сигнала, определялись значения ^o » ^1 • • • ^N-\ для (5)-(6). При заданной импульсной характеристике для значения M = 4 расчеты дали результат, представленный на рисунке 1.

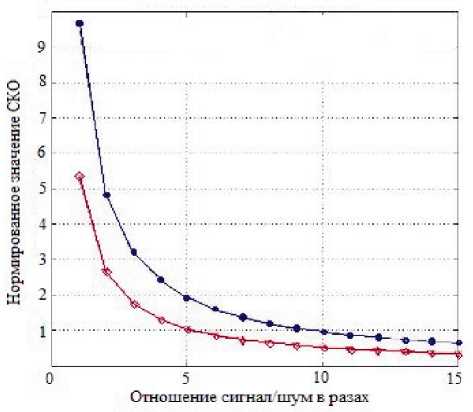
Рисунок 1. Зависимость среднеквадратической ошибки оценки импульсной характеристики от отношения «сигнал/шум» (верхняя кривая – метод наименьших квадратов, нижняя кривая – метод регуляризации)

При оценке методом наименьших квадратов и отношении «сигнал/шум» PJP_OIU^ нормированное СКО составляет ε = 9,66; а при ^./^„=15 значение ε = 0,64. При оценке методом регуляризации и отношении Pc / PqIU ^ нормированное СКО составляет ε = 5,32; а при ^./^„=15 значение ε = 0,35. Выбор значения параметра регуляризации возможно произвести путем нахождения минимального значения ошибки при разных значениях α в промежутке от 0,1 до 1,1 в формуле (6) при фиксированном отношении «сигнал/шум».

На рисунке 2 показан результат оценивания по методу регуляризации при фиксированных трех значениях отношений сигнал/шум и разных α. При α=0,1 значение нормированной СКО наименьшее.

Заключение

При использовании оптимальных (или ква-зиоптимальных) методов обработки сигналов OFDM в каналах с памятью в месте приема требуется знание импульсной характеристики канала. Использование двух методов получения оценок отсчетов импульсной характеристики показало, что при малых отношениях сигнал/шум нормированная среднеквадратическая ошибка оценки импульсной характеристики методом регуляризации меньше в 1,8 раз, чем оценка методом наименьших квадратов.

Значение ошибки для метода регуляризации минимально.

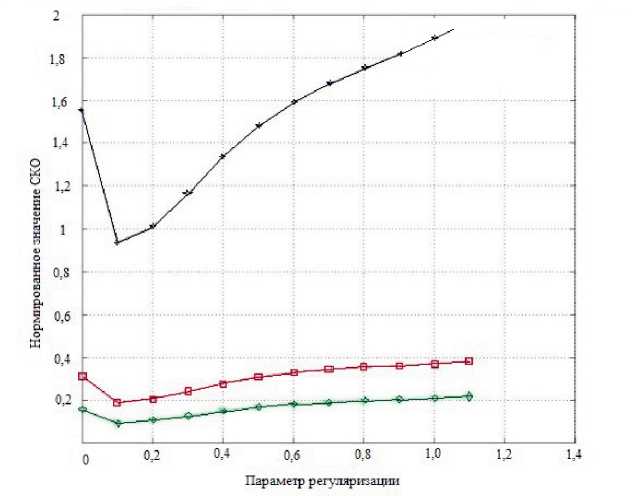
Рисунок 2. Зависимость нормированной среднеквадратической ошибки импульсной характеристики от параметра регуляризации (верхняя кривая - отношение сигнал/шум 1;

средняя кривая - отношение сигнал/шум 5; нижняя кривая - отношение сигнал/шум 10)