Методы оптимизации обобщенных тензорных сверток

Развитие вычислений с тензорами привели к созданию «Тензорные исчисления», отдельного активно развивающегося раздела математики, использующегося почти во всех областях механики, теоретической физики и прикладной математики. Можно выделить восемь основных операций, выполняемых над тензорами: сложение и вычитание, умножение на число, умножение тензоров, свертка, перестановка индексов, симметрирование и альтернирование. Каждая из перечисленных операций имеет широкое применение в различных научных дисциплинах [1].

Операция свертки тензоров (tensor contraction, TC) применяется в алгоритмах машинного обучения, таких как обучение и логический вывод в глубинных нейронных сетях (Deep Neural Networks, DNN) [2]. Квантовая химия широко использует TC в методах Хартри—Фока, а также при решении других задач, имеющих существенную практическую знчимость [3]. TC применяется при моделировании потоков несжимаемой жидкости на основе спектральных методов [4]. TC может быть использована для вычисления многомерного преобразования Фурье. В частности, трехмерное дискретное преобразование Фурье может быть вычислено через TC тензоров, полученных в результате применения двумерных дискретных преобразований Фурье [3].

Умножение матриц (matrix-matrix multiplication, MMM) и умножение матрицы на вектор (matrix-vector multiplication, MVM) могут рассматриваться как частные случаи TC, широко применяющиеся при решении прикладных задач. Примером использования MMM служит шифрование баз данных с последующим интеллектуальным анализом данных (Data Mining) [5]. MMM вычисляется во время обрезки весов (weight pruning), использующимся в машинном обучении [6]. Энергия корреляции молекул, рассматриваемая в квантовой химии, рассчитывается с использованием MMM [7]. MMM служит основой для большинства операций с матрицами, изучаемых в высокопроизводительных вычислениях [9]. В качестве примеров применения MVM можно привести обрезку весов, используемую в машинном обучении [10]; анализ графов [11]; расчет коэффициентов скорости реакции [12]. Большая часть операций с векторами реализована с использованием MVM [13–15]. MVM применяется при решении задач математической физики численными методами, в частности, при решении задач математической геофизики. Например, MVM успешно используется при решении задач гравиметрии или магнитометрии о нахождении поверхностей раздела сред по гравитационным или магнитным данным методом Левенберга—Марквардта [8].

TC может быть обобщена на произвольные полукольца матриц для решения задач о путях [16] (нахождение кратчайших путей, построение минимального остовного дерева, задача о самом широком пути и др.). Необходимость в решении таких задач возникает, в частности, в математических методах исследования операций, робототехнике, планировании размещения предприятий, транспортировке товаров, проектировании сверхбольших интегральных схем (VLSI design), при нахождении путей в картографических сервисах (MapQuest, Google Maps и др.).

В данной статье выполнен обзор методов оптимизации времени выполнения TC. В разделе 1 дана классификация подходов к оптимизации MMM и MVM, использующимся в качестве основы для оптимизаций TC. В разделе 2 описываются методы оптимизации TC. В заключении приводится обобщение результатов, полученных в ходе исследования.

• 1.    Оптимизация MMM и MVM

В силу широкой распространенности и практической значимости оптимизация MMM и MVM является отдельным предметом изучения высокопроизводительных вычислений [9]. Оптимизированные MMM и MVM могут применяться для оптимизации TC для тензоров большей размерности (Раздел 2). В данном разделе рассматриваются основные подходы к оптимизации MMM и MVM.

Специалисты в области приложений линейной алгебры одними из первых предложили использовать единый интерфейс к высокопроизводительным фундаментальным операциям, реализованным как стороннее программное обеспечение [17]. Более сорока лет таким интерфейсом являются базовые подпрограммы линейной алгебры (Basic Linear Algebra Subprograms, BLAS) [13–15]. Описываемые подпрограммы разделяются на три уровня. Первый уровень описывает операции над векторами, такие как, например, скалярное произведение и векторные нормы. На втором уровне интерфейса BLAS содержится описание операций над матрицами и векторами, таких как матрично-векторное произведение, а также описание подпрограмм для нахождения решения системы алгебраических уравнений с треугольной матрицей. Третьим уровнем описывается матричное произведение для различных типов матриц, построение симметричной матрицы и другие операции над матрицами. Интерфейс BLAS продолжает развиваться. BLAS++ [18], обновленная версия интерфейса

BLAS, используется в проектах, направленных на достижение экзафлопсной производи- тельности.

Применение BLAS требует новой реализации фундаментальных операций для каждой новой архитектуры процессора. В большинстве случаев они создаются экспертами в области высокопроизводительных вычислений, что требует значительных временных затрат. Реализации фундаментальных операций могут распространяться как открытое программное обеспечение (GotoBLAS [9, 19], OpenBLAS [20], BLIS [21]) и как проприетарные библиотеки, выпускаемые производителями аппаратного обеспечения (Intel’s MKL [22], IBM’s ESSL [23], ArmPL [24]).

Для сокращения времени разработки высокопроизводительных реализаций BLAS авторы библиотек ATLAS [25] и PHiPAC [26] предложили использование автонастройки (auto-tuninig). В ходе ее работы выполняется перебор всех возможных значений параметров рассматриваемой программы с целью получения реализации, имеющей наименьшее время выполнения. Как и в случае ручной настройки (manual-tuning), для выполнения автонастройки необходим доступ к целевой архитектуре, а также потенциально большие временные затраты. Было показано, что в случае ATLAS и MMM автонастройка может приводить к неоптимальным результатам [9].

Алгоритм 1: Вычисление матричного произведения

1 begin

for j = 0...N step Nc do for p = 0...K step Kc do

Упаковываем B(p:p + Kc — 1, j:j + Nc — 1) в массив Bc for i = 0...M step Mc do

I = i c : i c + M r — 1

j = jc : jc + Nr — 1

C c (I, j) += A c (I, P c ) • B c (p c , j)

end end end end end end

19 end

В качестве примера рассмотрим параметризованный алгоритм 1, применяемый для выполнения матричного умножения в фреймворке BLIS [17]. Перемножаемые матрицы A и B имеют размерность M \times K и K \times N , соответсвенно. Матрица C размерности M \times N содержит результат выполнения матричного произведения. В процессе выполнения алгоритма матрицы A и B разбиваются на блоки (рис. 1). Это позволяет многократно использовать элементы блоков, хранящихся в кэш-памяти. Размеры блоков Nc , Kc , Mc , Nr и Mr являются параметрами алгоритма. Их оптимальные значения могут определяться с помощью автонастройки и ручной настройки. C целью обеспечения последовательного доступа к операндам MMM используется упаковка данных. В процессе выполнения упаковки данных создаются временные выравненные в памяти массивы Ac и Bc , хранящие элементы перемножаемых матриц. Внутренний цикл вместе со своим содержимым называется микро-ядром MMM. Оно может генерироваться автоматически в процессе компиляции или реализовываться вручную в виде отдельной процедуры, написанной на языке ассемблера для целевой архитектуры [27, 28].

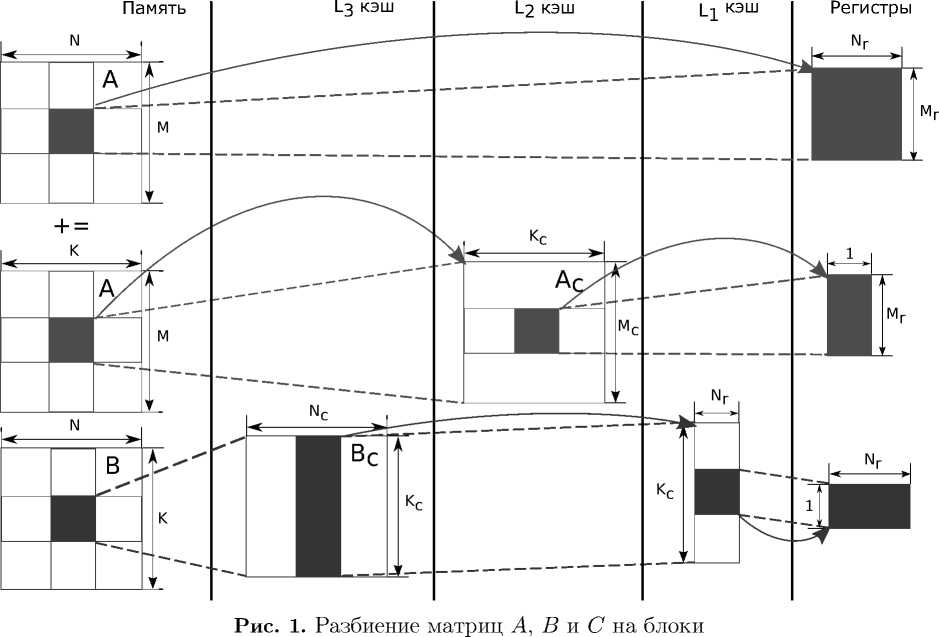
Автонастройка и аналитические техники могут применяться совместно с целью определения наилучшей оптимизации. Такой подход используется в компиляторах LGen [29] и Build to Order BLAS (BTO) [30]. LGen — это компилятор для базовых операций линейной алгебры с операндами малой размерности, известной на этапе компиляции. Для выполнения разбиений циклов, векторизации и слияния циклов LGen использует специализированный язык, позволяющий построить математическое представление программы для ее дальнейшей оптимизации. Результатом работы LGen являются функции на языке C, содержащие SIMD инструкции. Пример выражения, подаваемого на вход компилятору LGen, приведен на рис. 2. BTO компилирует последовательность выражений, содержащих матрицы и векторы, написанную на языке MATLAB, в оптимизированный код на языке C++. В процессе оптимизации BTO выполняет слияние циклов, основываясь на аналитических моделях и эмпирических методах. На рис. 3 показан пример программы на языке MATLAB, компилируемой BTO.

Фреймворк AUGEM [31] использует автонастройку совместно с эвристическими алгоритмами векторизации, распределения регистров и планирования команд. С помощью библиотеки POET [32] фреймворк AUGEM распознает части абстрактного синтаксического дерева программы на языке C, содержащие заранее определенный набор операций с матрицами, для их дальнейшей оптимизации. Пример операции с матрицами, распознаваемой фреймворком AUGEM показан на рис. 4.

alpha beta	= Scalar() = Scalar()
A	= Matrix(6, 11)
x	= Matrix(11, 1)
y z	= Matrix(6, 1) = Matrix(6, 1)

Generate(beta = (A*x+alpha*y)^T*z + Beta, opts)

Рис. 2. Пример выражения, подаваемого на вход компилятору LGen

GEMVER in v1 : vector, v2 : vector, u1 : vector, u2 : vector, alpha : scalar, beta : scalar, x : vector, y : vector inout A : dense column matrix out z : vector, w : vector {

A = A + v1 * u1’ + v2 * u2’ z = beta * (A’ * x) + y w = alpha * (A * z)

}

Рис. 3. Пример выражения, подаваемого на вход компилятору BTO mmCOMP(A, idx1, B, idx2, res):

tmp0=A[idx1]

tmp1=B[idx2] tmp2=tmp0*tmp1 res=res+tmp2

Рис. 4. Пример операции с матрицами, распознаваемой фреймворком AUGEM

С целью сокращения времени автонастройки множество значений исследуемых параметров может быть уменьшено за счет использования дополнительных измерений, выполняемых на целевой архитектуре. Такой подход называется итеративной компиляцией (iterative compilation) [33]. В ходе ее работы алгоритм оценивает параметры целевой архитектуры, такие как, например, количество промахов кэша для данной реализации. В дальнейшем полученная информация применяется для определения значений оцениваемых параметров. Улучшенная автонастройка (auto-fine-tuning) [34] представляет собой отдельную модификацию автонастройки. Ее отличие в использовании аналитических моделей, уменьшающих пространство поиска. Такие модели могут быть созданы с применением знаний о современных архитектурах процессоров и оптимизуруемой операции. В общем случае указанные улучшения не гарантируют устранения проблем автонастройки.

Можно избежать перебора значений параметров программы за счет моделирования потребления ресурсов используемой архитектуры. Для этого применяются модели гипотети- ческих процессоров, описывающих такие характеристики целевого процессора, как векторные регистры и векторные инструкции, иерархию кэш памяти [17, 34]. Аналитическое моделирование позволяет установить зависимости между потреблением ресурсов процессора и производительностью оптимизируемой программы. На момент написания данной работы не существует автоматического способа выполнения аналитического моделирования, позволяющего достичь высокой производительности оптимизируемой программы. Вследствие этого, как и в случае ручной настройки, аналитическое моделирование должно выполняться вручную специалистом.

Нахождение значений параметров программы, для которой выполнено аналитическое моделирование, и известны технические характеристики целевого процессора, выполняется за постоянное время и, вследствие этого, может использоваться в условиях ограниченного времени [28, 35]. Примером такой ситуации являются оптимизации, выполняемые промышленными компиляторами по умолчанию. С целью применения в процессе разработки и при компиляции готовых пакетов программ используемые оптимизации должны выполняться за наименьшее возможное время. Совместное применение автоматического распознавания кода, аналитических подходов и автоматической генерации кода позволяет автоматически получать высокопроизводительные реализации программ в процессе оптимизации, выполняемой компиляторами [28, 35].

В качестве примера модели гипотетического процессора рассмотрим модель, используемую в фреймворке BLIS для нахождения значений параметров реализации MMM [17]. Она может быть описана следующим образом [8]:

• •    « Архитектура загрузки/сохранения и векторные регистры: данные должны быть загружены в регистры процессора перед тем как с ними могут быть выполнены вычисления. Имеется N REG векторных регистров. Каждый из них может содержать N VEC значений размера S DATA . Если N REG равно 0, N VEC присваивается значение 1. Предполагается, что команды для работы с памятью могут выполняться одновременно с командами арифметики с плавающей точкой».

• •    « Векторные инструкции: пропускная способность процессора составляет N VFMA векторных операций смешанного сложения и умножения (vector fused multiply-add instruction, VFMA) за один такт. Отдельная VFMA выполняет N VEC умножений и сложений, составляющих VFMA. Минимальное количество тактов L VFMA , которое должно быть совершено перед началом выполнения новой зависимой по данным VFMA-инструкции, определяет задержку VFMA-инструкции».

• •    « Кэш-память: весь кэш данных — это множественно-ассоциативный кэш с политикой вытеснения последнего по времени использования (Least Recently Used, LRU). Каждый уровень кэша L i характеризуется следующими параметрами: размер линии кэша C L _i , степень ассоциативности W L _i , количество множеств N L _i , размер S L _i , где S L i = N L i C L i Wli . В случае полностью ассоциативного кэша Nl = 1».

Аналитическое моделирование может использоваться для минимизации перемещения данных и, как следствие, уменьшения времени работы приложения и его энергопотребления. Рассматриваемый алгоритм может быть изменен для достижения нижней асимптотической границы на перемещение данных в иерархии памяти, а также между процессорами [36, 37]. В частности могут изменяться формулы для нахождения значений параметров блочного алгоритма. Описанный подход обладает преимуществом в случае распределенных архитектур, имеющих большое количество отдельных узлов.

Кэш-независимые алгоритмы (сache-oblivious algorithms) [38] — это отдельный класс алгоритмов, позволяющих асимптотически оптимально использовать кэш-память, игнорируя ее отдельные параметры, такие как количество уровней кэша, длина кэш-линий, ассоциативность и т.д. Такие алгоритмы основываются на методе разделяй-и-властвуй (divide-and-conquer), разделяющем задачу на подзадачи до тех пор, пока данные отдельной подзадачи не смогут поместиться в каком-нибудь уровне кэш-памяти. Практическая оценка кэш-независимых алгоритмов показывает, что отсутствие в них таких механизмов, как предвыборка данных, затрудняет достижение производительности кода, созданного экспертами [39].

Несмотря на то, что MVM может рассматриваться как частный случай MMM, отношение количества вычислений, выполняемых MVM, к количеству перемещений данных из памяти меньше чем в случае MMM. Вследствие этого, методы для оптимизации MMM должны быть модифицированы для оптимизации MVM. В частности, из-за недопустимых издержек невозможно использование таких техник, как упаковка данных. В то же время возрастает необходимость в эффективной предвыборке данных, позволяющей уменьшить издержки чтения данных из памяти. Большинство подходов, используемых для оптимизации MVM, основаны на ручной настройке [9, 19–24, 40, 41] и автонастройке [25, 26]. Как и в случае MMM, аналитическое моделирование может применяться для оптимизации MVM с целью достижения производительности кода, оптимизированного вручную [8, 42]. Модификация представленной раннее гипотетической модели процессора может включать следующие дополнения, описывающее инструкции предвыборки [8]:

• •    « Инструкции предвыборки: за один такт процессора может быть выполнено N _prefetch инструкций. Задержка каждой инструкции составляет L _prefetch тактов процессора. Каждая инструкция может загрузить данные, размер которых равен C L _i ».

• 2.    Оптимизация TC

Особенности целевых архитектур процессоров и размерность рассматриваемой задачи могут использоваться совместно для автоматического получения оптимизированных реализаций BLAS. Так, например, библиотека LIBXSMM [43] генерирует низкоуровневые высокопроизводительные реализации MMM для некоторых архитектур от Intel и матриц, содержащих менее 80 \times 80 элементов. Для этих целей используется специальный алгоритм предвыборки данных и модифицированный алгоритм векторизации.

Фреймворк POCA [27] позволят получить высокопроизводительные микро-ядра, части MMM, содержащие векторные инструкции. На рис. 5 представлен пример микро-ядра MMM для процессоров с микроархитектурой Sandy Bridge [27]. POCA использует эвристический алгоритм для распределения регистров процессора на основе анализа графа зависимостей и особенностей целевой архитектуры, таких как количество векторных регистров и количество тактов, требуемых для выполнения отдельных векторных инструкций микроядра.

За последние двадцать лет прогресс во многих научных дисциплинах, таких как квантовая химия и общая теория относительности, основывался на моделировании физических систем, использующем TC. Несмотря на это, количество подходов к оптимизации TC намного меньше чем количество подходов к оптимизации MMM и MVM [44]. В данном разделе описываются основные методы оптимизации времени выполнения TC.

1 A0 = vload AP	//	a1, a2, a3>
2 B0 = vload BP	//	b1, b2, b3>
3 B1 = vshuffle B0 <1,0,3,2>	//	b0, b3, b2>
4 B2 = vshuffle B1 <2,3,0,1>	//	b2, b1, b0>
5 B3 = vshuffle B2 <1,0,3,2>	//	b3, b0, b1>
6 M0 = fmul A0, B0	//
7 C0 = fadd C0, M0	//	, c11, c22, c33>
8 M1 = fmul A0, B1	//
9 C1 = fadd C1, M1	//	, c10, c23, c32>
10 M2 = fmul A0, B2	//
11 C2 = fadd C2, M2	//	, c12, c21, c30>
12 M3 = fmul A0, B3	//
13 C3 = fadd C3, M3	//	, c13, c20, c31>
14 AP = add AP, 4	// AP +	=4
15 BP = add BP, 4	// BP +	=4
16 prefetch_0 (BP+64)	// 8 *	64 = 512(bytes)
17 prefetch_0 AN	// next	A block
18 AN = add AN, 32	// Mr *	8 = 32(bytes)

Рис. 5. Пример микро-ядра MMM для процессора с микроархитектурой Sandy Bridge

Рассмотрим определения d-мерного тензора и TC, позволяющие свести оптимизацию этой операции к оптимизации MMM и MVM:

Определение 1. d-мерный тензор Т Е R n u^{0 x} '" ^{x n ud}-1 может быть определен как множество элементов из \BbbR, описываемое следующим образом [45, 46]

В рамках данной работы будем предполагать, что элементы d-мерного тензора \scrT \in R n u^{0 x}-^{x n u}d-i. представлены многомерным массивом размерности n _u 0 X • • • X n u d -1 . В общем случае это утверждение не всегда верно.

Определение 2. Пусть \scrA , \scrB , и \scrC — это d A -, d B -, и d C - мерные тензоры, соответственно. Сворачиваемые индексы Л и В описываются кортежем P = p o •••p _t- i . Индексы С , а также свободные индексы Л и В описываются кортежами I = i o •••i r - i и J = j o •••j s — 1 , соответственно. Операция свертывания или свертки Л и В определяется ⁿ P0 ^{- 1} n Pt -1 ^{- 1}

как СТс (ij ) = £q-Л^а(1р ) • В^в (pj ) + 3-С^с<п), где Е= Е ••• Е , ^C (IJ), ^a(IP ), P                                               P    Ро=О     Pt-i=O и tb (PJ) — это перестановки индексов, а, 3 Е R [45, 46].

С целью оптимизации TC может быть использован программный код оптимизированных MMM и MVM, полученный в результате выполнения алгоритмов, описанных в предыдущем разделе. Так, например, метод Transpose-Transpose-GEMM-Transpose (TTGT) [47], применяемый в различных прикладных библиотеках (MATLAB Tensor Toolbox [48], NumPy [49], Eigen [50] и др.), выполняет перестановку индексов тензоров с целью их представления в виде матриц и использования MMM. Для выполнения таких перестановок требуются дополнительное время и память.

Метод Loops-over-GEMMS (LoG) [44] представляет сворачиваемые тензоры как наборы матриц, для которых выполняется MMM. Производительность LoG зависит от размера 26 Вестник ЮУрГУ. Серия «Вычислительная математика и информатика»

таких матриц, а также расположения тензоров в памяти [44]. Так, например, в случае свертки 3-мерного тензора \scrA \in \BbbR ^{m \times n \times k} и 2-мерного тензора \scrB \in \BbbR ^{k \times l} в 3-мерный тензор к — 1

С G ^ m x n x l , имеющей следующий вид С _ар_р = ^ А _арз • В зр + С _ар_р , LoG вычислит MMM 5 =0 для каждого из n значений индекса \beta .

Для решения задач в таких научных областях, как, например, квантовая химия, созданы модификации метода TTGT для распределенных вычислений. Такие подходы применяют разбиение тензоров на блоки и другие техники для уменьшения передачи данных в иерархии памяти, а также между процессорами. Примерами библиотек, содержащих реализации описанных методов, служат Tensor Contraction Engine [47], Cyclops Tensor Framework [51], libtensor [52], TiledArray [53, 54] и др.

Для сокращения издержек, связанных с перестановкой индексов тензоров, можно ис- пользовать только микро-ядра, части реализации оптимизированного MMM, содержащие векторные инструкции на языке ассемблера. Такой подход применяется в методах GEMM-like Tensor-Tensor multiplication (GETT) [46] и Tensor-Based Library Instantiation Software (TBLIS) [45]. Как и в случае алгоритма 1 для вычисления MMM подходы GETT и TBLIS упаковывают элементы операндов TC во временные одномерные массивы c целью дальней- шего использования кода микро-ядра MMM.

В отличии от GETT, TBLIS представляет тензоры в виде матриц, что позволяет явно выполнять разбиение матриц на блоки и другие трансформации, применяемые в алгоритме 1. В качестве примера применения такого представления рассмотрим d-мерный тензор T G K n "° ^х" ' ^хп^ - 1 . A _{U 0} ..._{U d}_ ₁ , элемент тензора T , расположен в памяти со смеще- d — 1     d — 1

нием     u k      n u _l . Пусть свободные и сворачиваемые индексы тензора \scrT описываются

• к=0

представлено в виде    ik k=0

dp —1    dp —1          dI —1

+     pk      npl =       ik      nil nP k=o   l=k+1       \к=0   l=k+1 /

• d p — 1     d p — 1        _ __

+ Рк Рк П npl = Inp + P. Если рассмотреть смещение в памяти iN + j элемента Mj к=0

некой матрицы размерности M\timesN, то можно вывести формулы, позволяющие логически представить тензор \scrT в виде матрицы размерности nI \times nP :

dI —1

I = Eik П ni, к=0 l=k+1 dp —1

np = П npi, ni = П nil , l=0

• dp —1

• P = 52 Рк П npi. k=0

Другое отличие GETT в применении автонастройки для нахождения наилучших значений параметров разбиения и способов выполнить упаковку элементов тензора. Использование автонастройки позволяет повысить производительность получаемого кода, но делает невозможным применение GETT в условиях недоступности целевой архитектуры и ограниченности времени выполнения. Кроме этого GETT не поддерживает тензоры, размер которых неизвестен на этапе компиляции.

Подход, используемый в TBLIS, может быть объединен с аналитическим моделированием для устранения необходимости в коде MMM, оптимизированном вручную. Полученный метод совместно с алгоритмами для распознавания кода TC может применяться автоматически в процессе оптимизации, выполняемой промышленным компилятором по умолчанию во время компиляции и кросс-компиляции. На рис. 6 изображен комплекс автоматизированной оптимизации обобщенных тензорных операций (АООТО) [8, 28]. В процессе работы АООТО фронтенд Clang [55] строит промежуточное представление программы, используемое комплексом оптимизаций Polly [56]. Polly создает специальное математическое представление программы с целью распознавания TC и ее оптимизации с применением аналитического моделирования и метода, предложенного в TBLIS. Библиотека LLVM Core [55] использована для генерации ассемблерного кода целевой архитектуры процессора.

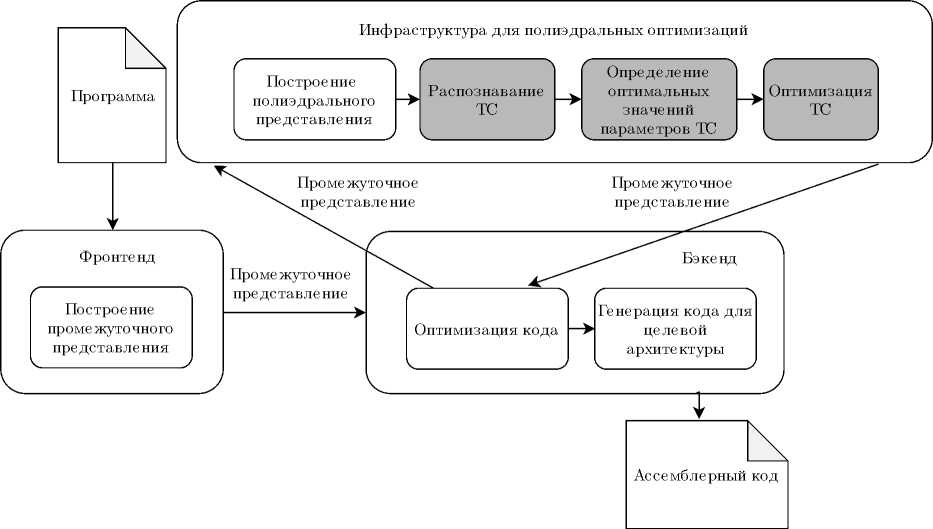
Рис. 6. Комплекс программ АООТО

Для оптимизации TC могут применяться последовательности стандартных оптимизаций циклов (перестановка циклов, разбиение циклов на блоки, размотка циклов, векторизация и др.). Такие подходы зависят от размерности тензоров и их расположения в памяти [57]. В частности, производительность TC для задач малой размерности может быть улучшена за счет векторизации циклов [58]. Для задач большой размерности может применяться генератор кода циклов для графических ускорителей [59].

Заключение

TC является операцией «Тензорного исчисления», отдельного раздела математики, созданного для решения теоретических вопросов, требующих более общего исчисления чем векторное. TC, обобщение TC на произвольные полукольца матриц, а также MMM и MVM, частные случаи TC, широко применяются как в теории, так и на практике. Вследствие этого, эффективное выполнение TC имеет существенную практическую значимость.

В статье представлен обзор походов к оптимизации TC. Большинство таких методов основывается на преобразовании тензоров к матричной форме с целью применения оп- тимизаций MMM и MVM, или использования отдельных частей оптимизированного кода MMM и MVM. Описывается представление тензоров, позволяющее свести оптимизацию TC к оптимизации MMM и MVM.

Рассмотрены подходы к оптимизации MMM и MVM, реализованные в виде проприетарных библиотек и свободного программного обеспечения. Большая их часть основывается на ручной настройке и самонастройке, осложняющих использование в процессе кросскомпиляции, выполняемой промышленными компиляторами, и других условиях ограниченного времени и отсутствия доступа к целевой архитектуре. Время работы таких методов может быть уменьшено за счет применения аналитического моделирования, устанавливающего зависимость между использованием ресурсов гипотетического процессора и производительностью программы. В случае распределенных архитектур время выполнения MMM и MVM может быть уменьшено достижением нижней асимптотической границы на перемещение данных в иерархии памяти, а также между процессорами.