Методы оптимизации планов застройки района

Рассматриваются задачи оптимальной застройки района по критерию прибыли. Пусть имеется n участков возможного строительства и m типов проектов. Задача состоит в выборе числа домов каждого типа, обеспечивающих максимальную прибыль от продажи квартир. Для решения задач предлагается метод дихотомического программирования.

Имеются m типов домов. Стоимость строительства домов i -го типа С_i ( х_i ) зависит от числа x_i домов i - го типа, включенных в план застройки, и является вогнутой функцией 0 <  х , <  b i . Имеются n участков для строительства домов. Строительство дома i- го типа на участке j требует дополнительных затрат Δ _i j . Известно количество S_i жилой площади домов i -го типа и рыночная цена р_i 1 м 2 жилой площади домов i -го типа. Обозначим y j = 1, если на j -м участке строится дом i -го типа, и у у = 0 в противном случае, i = 1, m , j = 1, n .

Прибыль от продажи квартир x i = Е У у домов i -го типа равна

j

Q i = P i s i x i ^- Е ^A уУу ^- C i ( x i ) .

j

Тогда возникает задача следующего типа: определить {уу} i = 1, m, j = 1, n максимизирующие Q=Е( Pisi- Aj) Уу - Е ci Е Уу , i,j                                         i j при ограничениях

Е У у = 1, ^j = 1, n ,

i

Е У у- - b , i = 1, ^m .

i

В линейном случае C i ( x i ) = q i x i и задача принимает вид

Q=Е tij • Уу, i,j где tij = pisi-Aij- qi, что является частным случаем транспортной задачи [1, 2].

Если приять во внимание ограничение на площадь земельного участка, то это приводит к появлению дополнительного ограничения в задаче. Обозначим: t i – площадь, требуемая для строительства дома i -го типа; N – общая площадь земельного участка, отведенного под строительство жилых домов. Ограничимся случаем линейной зависимости стоимости строительства от числа домов каждого типа. Задача заключается в максимизации площади жилых помещений

5(x) = £xisi,(1)

i при ограничениях

C (x )=E ci • xi- R,

i

T(x) = £ti • x- N.(3)

i

Получили задачу целочисленного линейного программирования с двумя ограничениями. Для ее решения можно применить стандартные программы [3–6].

Рассмотрим, однако, другой подход, в основе которого лежит метод сетей всех допустимых решений (ВДР), предложенный В.Н. Бурковым. Идея метода состоит в следующем. Рассмотрим первое ограничение (2) и построим сеть всех допустимых решений для этого ограничения. Способ построения такой сети описан, например, в [1, 7, 8]. Примем для упрощения вычислений, что дома строятся пакетами. Положим x_i = 1, если строится пакет домов i -го типа (пакет содержит определенное число домов), и x i = 0 в противном случае. Алгоритм рассмотрим на примере.

Пример 1.

• 1    шаг. Пусть ограничение (2) имеет вид

x 1 + 2 x 2 + 2 x₃ + 2 x 4 + x₅ <  5.

Соответствующая сеть всех допустимых вариантов приведена на рис. 1.

• 2    шаг. Рассмотрим ограничение (3)

• 6    x 1 + 2 x 2 + 2 x ₃ + 3 x 4 + 4 x ₅ <  8 .

Соответствующая сеть приведена на рис. 2

Определение. Проблемной вершиной сети всех допустимых решений (сеть ВДР) назовем вершину, не принадлежащую последнему слою (в нашем случае слою 5), имеющую сеть захода больше 1. Заметим, что сеть ВДР рис. 1. имеет шесть проблемных вершин, а сеть ВДР рис. 2. имеет одну проблемную вершину (3; 2).

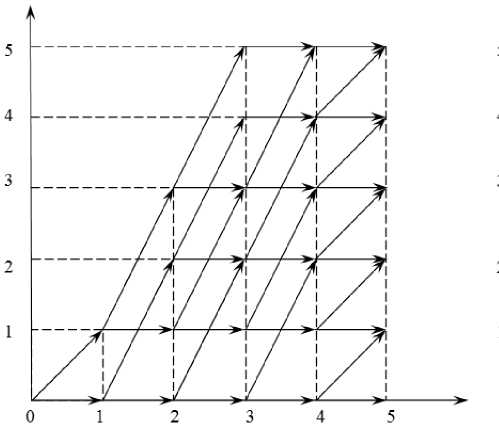
Рис. 1

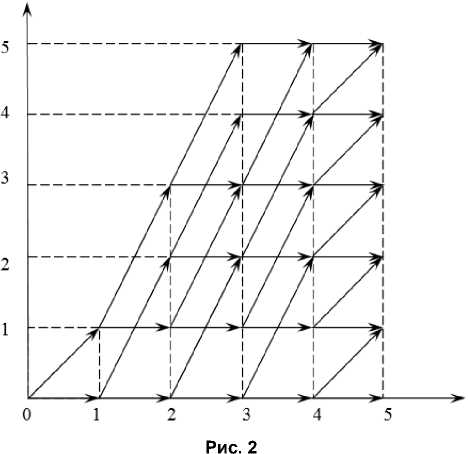
Вершины сети будем обозначать номером переменной (в нашем случае 3) и величиной требуемой площади земельного участка (в нашем случае 2).

Управление в социально-экономических системах

• 3    шаг. Выбираем сеть с минимальным числом проблемных вершин. Назовем эту сеть основной. Длины дуг сети берем равными соответствующим коэффициентам другой сети, в нашем случае первой (длины дуг приведены у дуг на рис. 2 в скобках).

Определяем кратчайшие пути в каждую вершину основной сети. Если длина кратчайшего пути в вершину больше правой части первого ограничения, то есть 5, то соответствующую дугу исключаем. Исключенные дуги перечеркнуты на рис. 2.

Имеет место следующая теорема.

Теорема 1. Сеть ВДР содержит все допустимые решения системы неравенств ( 2 ) , ( 3 ) .

Доказательство. Если длина кратчайшего пути в какую-либо вершину сети превышает пра- вую часть первого ограничения, то не существует ни одного допустимого решения задачи, которому соответствуют пути, заканчивающиеся в данной вершине. Поэтому соответствующую заходящую дугу можно исключить. В нашем примере для дуги [(3; 4), (4; 7)] имеет место

Х ( 3; 4 ) + c ₄ = 6 >  5,

Х (3; 4) - потенциал вершины (3; 4).

Поэтому эту дугу, а значит и следующую

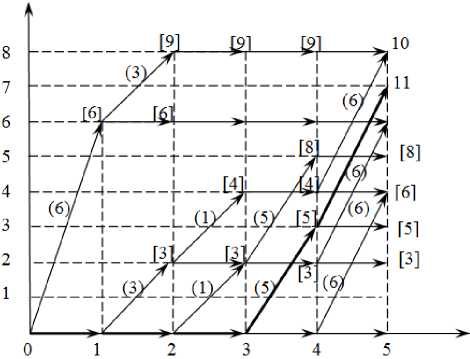
Рис. 3

за ней дугу [(4; 7), (5; 7)] исключаем. Полученная сеть приведена на рис. 3.

• 4    шаг. Полагаем длины дуг сети рис. 3. равными соответствующим коэффициентам целевой функции. Пусть целевая функция имеет вид

• 6    x 1 + 3 x 2 + x ₃ + 5 x ₄ + 6 x ₅.

Определим путь максимальной длины.

Теорема 2. Длина максимального пути в сети ВДР определяет оценку сверху для исходной задачи ( 1 )–( 3 ) .

Доказательство. Следует из теоремы 1, поскольку сеть ВДР содержит все допустимые решения.

В примере длина максимального пути равна 11 (путь выделен на рис. 3).

Следствие. Если среди путей максимальной длины существует путь, для которого соответст- вующее решение задачи удовлетворяет первому ограничению, то это мальным. Доказательство очевидно.

решение является опти-

В нашем случае это именно так. Пути максимальной длины соответствует решение х = (0, 0, 0, 1, 1), которое удовлетворяет неравенству (2). Поэтому это решение является опти-

мальным.

Теорема 3. Если путь максимальной длины не содержит проблемных вершин, то соответ- ствующее решение является оптимальным.

Доказательство. Если путь не содержит проблемных вершин, то, очевидно, соответствующее решение удовлетворяет неравенству (2). Если решение, соответствующее пути максимальной длины, не удовлетворяет ограничению (2), то применяем метод ветвей и границ, причем ветвление проводим по переменной, соответствующей одной из проблемных вершин.

Приведем пример.

Пример 2. Пусть ограничение (3) имеет вид

3 x 1 + 3 x 2 + 2 x ₃ + 3 x ₄ + 4 x ₅ <  10,                                                                 (4)

а целевая функция

S ( x ) = x i + 6 x 2 + 5 x ₃ + 4 x ₄ + 2 x ₅,                                                                (5)

Построим сеть ВДР для ограничения (4) рис. 4.

Число проблемных вершин равно 5, что меньше чем для сети рис. 1. Поэтому в качестве основной берем сеть рис. 4. Подставляя длины дуг из ограничения (2), получаем, что ни одна дуга не исключается. Берем длины дуг равными коэффициентам целевой функции (5) и определяем путь максимальной длины (длины дуг указаны над уровнем ограничения 10). Путь максимальной длины Ц = [(0; 0); (1; 0); (2;3); (3; 5); (4; 8); (5;10)] • Его длина равна 15. Соответствующее решение х = (0, 1, 1, 1, 0). Однако это решение не удовлетворяет неравенству (2). Поэтому 15 – это оценка сверху. Применяем метод ветвей и границ. Для ветвления берем проблемную вершину (4; 8), то есть переменную х. Делим множество всех решений на два подмножества. В первом подмножестве х4 = 1, а во втором х4 = 0.

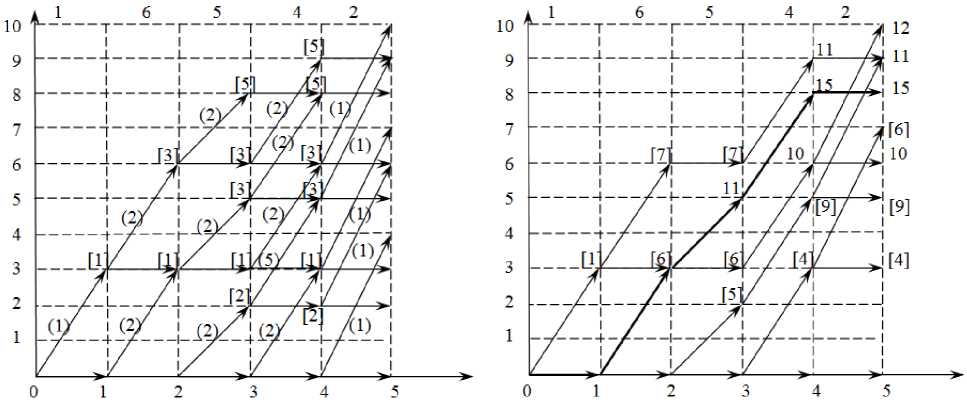
Рис. 4

Рис. 5

Оценка первого подмножества .

Исключаем дуги, соответствующие х 4 = 0, получаем сеть рис. 5.

Оптимальное решение определяется путем максимальной длины. Этот прежний путь длины 15.

Оценка второго подмножества .

Если х4 = 0, то путь максимальной длины [(0; 0); (2; 3); (3; 5); (4; 5); (5; 9)] с длиной 13. Выби- раем первое подмножество (х4 = 1). Теперь для ветвления берем проблемную вершину (2; 3), то есть переменную х2.

Оценка первого подмножества (х 2 = 1) .

Если х2 = 1 , то путь кратчайшей длины в вершину (4; 8) будет равен 6 > 5. Поэтому дугу [(2; 3); (3; 5)] исключаем. Путь максимальной длины [(0; 0); (1; 0); (2; 3); (3; 3); (4; 6); (5; 0)] с дли- ной 12.

Оценка второго подмножества (х 2 = 0) .

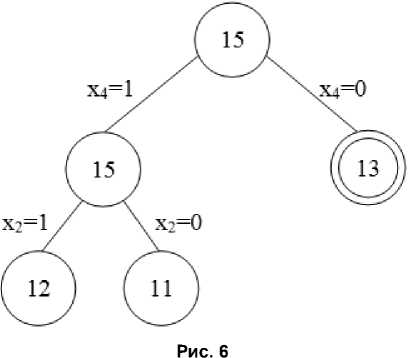
Путь максимальной длины [(0; 0); (1; 0); (2; 0); (3; 2); (4; 5); (5; 9)] с длиной 11. Теперь выбираем подмножество ( х ₄ = 0) с максимальной оценкой 13. Соответствующее решение х = (0, 1, 1, 0, 1) удовлетворяет ограничению (2) и поэтому является оптимальным. Дерево ветвлений приведено на рис. 6.

В данном случае число ветвлений равно 2. В общем случае число ветвлений не превышает числа 2 ^q , где q – число проблемных вершин.

Получим нижнюю оценку для задачи (1)–(3). Для этого на сети рис. 4 ищем пути не минимальной, а максимальной длины в каждую вершину (рис. 7).

Если длина максимального пути превышает 5, то соответствующая дуга удаляется. В нашем примере это дуга [(3; 5); (4; 8)] .

Эта сеть содержит только допустимые пути, то есть пути, которым соответствуют решения, удовлетворяющие обоим неравенствам. Определяем в этой сети пути максимальной длины, беря

Управление в социально-экономических системах

в качестве длин дуг коэффициенты целевой функции (5) рис. 8. Определяя пути максимальной длины в этой сети, получаем решение х = (0, 1, 1, 0, 1), которое является оптимальным. Однако это не всегда так, поскольку сеть может содержать не все допустимые пути.

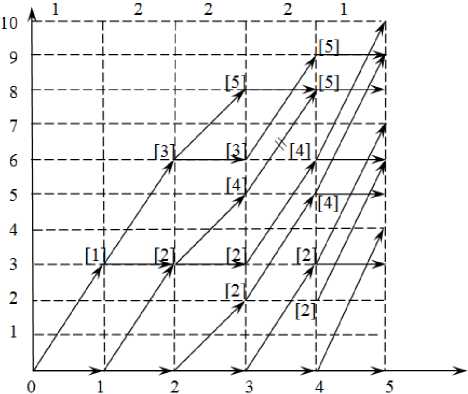
Рис. 7

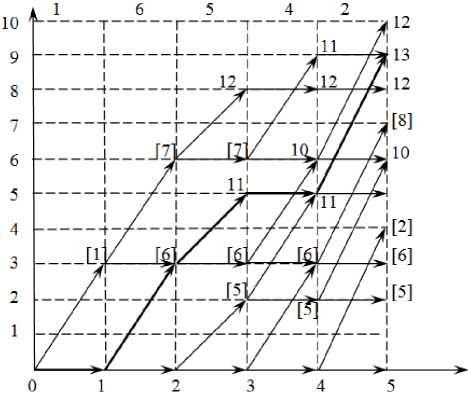
Рис. 8

Рассмотренный алгоритм естественно обобщается на случай, когда х i принимает значения не только 0 или 1, а любые целочисленные значения на отрезке [ 0; b i ] , i = 1, n . В этом случае просто несколько усложняется построение сетей всех допустимых решений.

Можно не строить сеть ВДР, а использовать табличный способ вычислений.

Обозначим у1 = (0; a11; a12;...; a1 m), где a1 j = (t1 j;c1 j;51 j) варианты первой обобщенной переменной (предположим, что ограничение (3) является основным), у2 = (0;a21;a22;...;a2m2), где a2 j = (12 j; c2 j;52 j) варианты второй обобщенной переменной.

• 1 шаг. Вычисляем

У12 = (0; a1 j + a2k ) , j = 1, m1, k = 1, m2 , где

• ^a 1 j + a 2 k = ( t 1 j + t 2 k ^; c 1 j + c 2 k ^{; 5} 1 j + ⁵ 2 k ) ^.

• 2 шаг. Если существуют ( j , k ) и ( p , r ), такие что t 1 j + t 2 k = t 1 p + t 2 r ,

то определяем

• c 1 j + c 2 k = c 1 p + c 2 r = ^C [ ( ^j , k ) , ( P , r ) ] = min [ c 1 j + c 2 k ; c 1 p + c 2 r ] ,

• ⁵ 1 j + ⁵ 2 k = ⁵ 1 p + ⁵ 2 r = ^{5 [} ( ^j , k ) , ( P , r ) ] = max [ ⁵ 1 j + ⁵ 2 k ; ⁵ 1 p + ⁵ 2 r ^] .

Соответствующий вариант назовем проблемным.

• 3 шаг. Все варианты, для которых T = t 1 j + 1 _{2 k} >  N , исключаем из рассмотрения. Исключаем из рассмотрения также варианты, для которых C = c 1 j + c _{2 k} >  R . В результате получаем таблицу вариантов обобщенной переменной у = ( у 1 ; у ₂ ) .

Если число переменных равно n , то потребуется ( n – 1) основных шагов, чтобы получить все допустимые варианты строительства.

Заметим, что по сути дела мы получаем дерево, содержащее все допустимые (и возможно недопустимые) решения задачи (1)–(3). Поэтому по аналогии с теоремами 1–3 имеет место теорема 4.

Теорема 4. Вариант j (n – 1) основного шага с максимальным третьим числом S j определяет оценку сверху для исходной задачи, причем, если соответствующее решение удовлетворяет ограничению (2), то оно является оптимальным.

Доказательство. Проводится аналогично доказательству теорем 1–3.

На практике учет рисков, как правило, производится на основе качественных шкал. В частности, в Сбербанке России применяется трехбалльная шкала: 1 – низкий риск, 2 – средний риск, 3 - высокий риск. Примем, что каждый тип домов имеет определенную оценку риска r i , i = 1, n . Для учета рисков введем ограничения на суммарный риск варианта застройки

R ( x ) = z rx i ^ Q . (6) i

Для решения задачи (1) – (3), (6) применим метод дерева допустимых решений, удовлетворяющих неравенствам (2) и (3), и повторим основные шаги алгоритма его построения, заменив параметры c i (вторые числа каждого варианта) на параметры r i .

Таким образом, для задачи максимизации жилой площади при ограничениях на стоимость строительства и площадь земельного участка разработан алгоритм сетей допустимых решений для получения верхних оценок. Алгоритм обобщен на случай учета рисков строительства.