Методы оптимизации развозки грузов потребителям несколькими транспортными средствами

В настоящее время актуальным управленческим решением становится оптимизация производственных процессов на всех этапах. Грузовой транспорт – одна из наиболее важных отраслей народного хозяйства. Увеличение эффективности работы логистической компании обеспечивается не только точной организации поставок, но и своевременной доставкой груза в пункты маршрута. Организация работы погрузочно-разгрузочных пунктов, грамотно соотнесенная с работой транспортных средств, становится неотъемлемой частью эффективного функционирования автотранспортного предприятия. Именно поэтому возникает потребность в оптимизации развозки грузов посредством привлечения математических методов.

Задача развозки – это транспортная задача по доставке негабаритных грузов из распределительного центра, например, оптовой базы, склада, грузового терминала и пр., множеству получателей, расположенных в районе действия транспортной компании. Она является обобщением известной задачи коммивояжера, от которой отличается условием ограниченности грузоподъемности применяемого транспортного средства и, как следствие, при движении по маршруту необходимостью неоднократного возвращения на базу для пополнения перевозимого груза для обеспечения всех клиентов. Математически стандартная задача развозки формулируется следующим образом.

Дано: n – число клиентов, которым необходимо доставить грузы; q – вектор заказов, определяющий количество груза, доставляемого каждому клиенту; M – матрица расстояний между всеми клиентами и базой, а также клиентов между собой. С – грузоподъемность применяемого транспортного средства (ТС).

Определить кратчайший маршрут развозки груза, обеспечивающий потребности всех клиентов.

Реальная ситуация отличается от сформулированной канонической задачи чаще всего тем, что помимо пройденного расстояния необходимо каким-то образом учитывать и максимальное время развозки. Если минимизация суммарного расстояния учитывает интересы перевозчика, снижая расход горючего, а значит, себестоимость развозки, то минимизация времени отвечает интересам клиентов, нуждающихся не просто в доставке груза, но и в обеспечении минимального срока доставки. Системный подход подразумевает рассмотрения любой ситуации с различных сторон и учета всех возможных интересов. Поэтому дополним сформулированную задачу следующим условием: требуется распределить клиентов по нескольким одновременно работающим ТС грузоподъемности C, чтобы максимальное время выполнения заказа было минимально.

Поясним последнее условие. Пусть после определения кратчайшего маршрута развозки определилось необходимое число рейсов m и t ∑ – суммарное время всех поездок. Если для выполнения заказа привлечь несколько автомобилей и заставить их работать одновременно, то, очевидно время выполнения всего заказа уменьшится, и оно будет равно t max – максимальное время работы одного автомобиля. Поскольку время реализации индивидуальных маршрутов в общем случае различается, то задача будет состоять в том, чтобы оптимально распределить ТС по индивидуальным маршрутам для минимизации t max .

Материалы и методы

Рассмотрим пример. Имеется 30 пунктов развозки и склад, откуда необходимо развести груз. Массы заказанных грузов приведены в таблице 1.

Таблица 1.

Массы заказанных грузов

Table 1.

Weights of ordered goods

№	Масса груза, кг Weight of cargo, kg	№	Масса груза, кг Weight of cargo, kg	№	Масса груза, кг Weight of cargo, kg
1	1120	11	300	21	490
2	540	12	226	22	512
3	690	13	356	23	256
4	328	14	420	27	388
5	620	15	236	25	288
6	760	16	222	26	430
7	236	17	552	27	368
8	256	18	460	28	252
9	620	19	292	29	156
10	370	20	920	30	312

Известны также матрица M расстояний между объектами и время преодоления этих расстояний плюс время разгрузки. Необходимо составить маршруты развозки ТС грузоподъемностью 1500 кг.

Воспользуемся каким-либо из многочисленных алгоритмом оптимизации развозки [1- 10] для составления системы кольцевых маршрутов. Результат приведён таблице 2. В последнем столбце приведено расчетное время поездки по маршруту с учётом дорожной ситуации и времени разгрузки.

Таблица 2.

Кольцевые маршруты по алгоритму Кларка–Райта

Table 2.

Clark-Wright loop routes

Маршрут Route	Маршрут (0–склад) Route (0–warehouse)	Перевезенный груз, кг Carried cargo, kg	Расстояние, км Distance, km	Время, мин Time, min
1	0–1–0	1120	5,72	48,6
2	0–3–2–0	1230	10,58	85,2
3	0–13–6–0	1116	7,35	74,8
4	0–16–15–12– 7–0	1476	11,04	118,5
5	0–18–20–0	1380	8,03	76,8
6	0–19–27–21– 29–0	1306	13,18	134,5
7	0–24–10–9–0	1306	8,32	84,6
8	0–26–25–23– 22–0	1486	20.58	161.8
9	0–28–5–4–0	1200	15,3	128,1
10	0–30–17–14– 0	1284	8,58	94,4

При использовании одного ТС время выполнения всего заказа составит 1007,3 мин или 16 ч 48 мин. Поставим цель сократить это время за счет использования нескольких ТС, производящих развозку в одно время. Как было сказано выше, проблема, очевидно, состоит в том, чтобы оптимально распределить ТС по индивидуальным маршрутам для минимизации времени выполнения всего заказа. Предлагается для решения этой задачи воспользоваться алгоритмом решения известной задачи «Упаковка предметов в контейнеры» [11–17]. Она формируется следующим образом.

Имеется конечное множество U = { u 1 , u 2 …, u n } объектов, «размеры» s ( u ) которых заданы и представлены рациональными числами. Требуется найти такое разбиение множества U на подмножества U 1 , U 2 …, U k , чтобы сумма размеров объектов в каждом подмножестве не превосходила некоторого положительного числа H , и чтобы число классов разбиения k было минимальным. Наиболее типичная интерпретация задачи, по которой она была названа – требуется упаковать объекты, принадлежащие каждому подмножеству в контейнеры размера H , так чтобы число контейнеров было минимально.

Данная задача имеет множество приложений, мы предлагаем еще одно: объекты ассоциировать с полученными кольцевыми маршрутами, s ( u ) – со временем поездки по маршруту, подмножества U j отождествлять с множеством маршрутов, реализуемых одним ТС. Под H следует понимать максимально допустимое общее время развозки. Конкретное значение H не задано в условиях. Очевидно, что его минимальным значением может быть максимальное значение s ( u ), поскольку нет смысла разбивать

Задача упаковки относится к классу NP -трудных задач в сильном смысле и не имеет точного алгоритма решения для произвольных исходных данных. При малых n можно воспользоваться полным перебором, для больших n разработано несколько приближенных алгоритмов примерно одинаковой эффективности. Наиболее простым является алгоритм «First fitted (FF)» – «первый подходящий» [14, 17]. Он состоит в том, что объекты помещаются в контейнеры в порядке живой очереди. Очередной предмет u i помещается в контейнер с наименьшим номером, у которого сумма размеров уже помещенных в него предметов не превосходит H – s ( u i ), т. е. в первый «допустимый» контейнер.

Более эффективный алгоритм, т. е. дающим лучший результат в смысле минимума целевой функции можно получить, если заметить, что наихудшей для алгоритма FF будет ситуация, когда в упорядочении объектов предметы с меньшими размерами идут раньше предметов с большими размерами. Тогда первые контейнеры будут забиты мелкими объектами, а для крупных объектов свободного места не останется, и последующие контейнеры будут оставаться полупустыми. Отсюда улучшенным вариантом алгоритма является алгоритм «First fitted with decreasing (FFD)» – «первый подходящий с убыванием» [17]. От первого варианта он отличается тем, что перед упаковкой объекты упорядочиваются по уменьшению размеров и к полученной очереди применяется алгоритм FF.

Воспользуемся алгоритмом FFD для оптимального распределения ТС по построенным маршрутам. Положим «размер» контейнеров равным 211 минут или 3 часа 31 минута. Результат расчетов приведен в таблице 3.

Таблица 3.

Результаты расчета по алгоритму «первый подходящий с убыванием»

Table 3.

Calculation results according to the "first fit with descending" algorithm

ТС vehicle	Продолжительности составляющих маршрутов, мин Duration of component routes, min	Суммарное время, мин Total time, min
1	161,8 48,6	210,4
2	134,5 74,8	209,3
3	128,1 76,8	204,9
4	118,5 85,2	203,7
5	94,4 84,6	179,0

При таком распределении максимальное время развозки составит 210,4 мин, или 3 часа 31 минута, т. е. в 4,78 раза меньше, чем при использовании одной единицы ТС. При этом придется задействовать пять единиц ТС, которые будут загружены примерно в одинаковой степени, за исключением ТС № 5.

Попробуем получить более экономный вариант по количеству ТС. Зададимся целью обеспечить развозку тремя единицами ТС. Для подбора подходящего значения H нам понадобится метод оценки числа контейнеров независимый от используемого алгоритма. Прежде всего, определим примерный минимальный размер контейнера при заданном их количестве к . Очевидно H_mm = ^ s ( u J Jk .

В нашем примере при k = 3 получим H min = 335,8. С другой стороны, нижней оценкой числа контейнеров при заданном H является величина

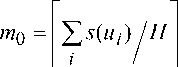
Обозначим L = {1…, n} – множество номеров объектов, wi = s(ui) / H – размеры объектов в долях H, 0 < Wi < 1. Для произвольного а е[0; 1/2] положим L 1 = {iеL \ wi > 1 - а} - множество номеров крупных предметов; L2 = {i еL | 1 - а > Wi > 1/2} - множество номеров средних предметов; L3= {i еL | 1/2 > Wi > а} -множество номеров мелких предметов.

Тогда для любого а е [0; 1/2] величина

M 1(а) = L1+| L21 + max М £ w - \ L2I +^ w >

I е L

I е L 2

является нижней оценкой для оптимального числа контейнеров OPT ( L ).

Поясним оценку (1). Каждый предмет из множества L 1 ∪ L 2 требует отдельный контейнер. Поэтому в любом допустимом решении не менее | L 1 | + | L 2 | контейнеров. Предметы из множества L 3 невозможно поместить вместе с предметами из L 1 . Значит, они лежат либо вместе с предметами из L 2 , либо в отдельных контейнерах. В контейнерах для L 2 осталось

S = I L 2 I -"У, w свободного пространства. Сле- ^{1 е} L 2

довательно, для предметов из множества L 3

требуется как минимум у w - S отдельных

I^е L 3

контейнеров.

Похожим способом получается другая оценка:

M 2 ( а ) = L Н L 2 1 +

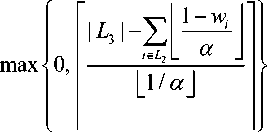
Для получения оценки (2) заменим размер каждого предмета из множества L 3 на α. Тогда в один контейнер войдет ^ 1/ а _| предметов, и для множества L 3 потребовалось бы P I L 3 I/L 1/ а дополнительных контейнеров. Но часть предметов из L 3 можно уложить в контейнеры для L 2 . Каждый из них имеет 1 – w i , i е L ₂ свободного места, где поместится ^ ( 1 - w_t )/ а | предметов из L 3 .

Поскольку каждая из величин (1) и (2) является нижней оценкой для OPT(L) при некотором а, то чтобы применить эти оценки на практике, надо найти максимальные значения M1 (а) и M2 (а) по всем а е [0; 1/2]. Причём доказано, что в качестве значений а достаточно брать а = Wi < 1/2. Тогда в качестве обобщающей нижней оценки Мартелло и Тота можно использовать m = max {max(Mx (а)); max(M2 (а))}. (3) ( а а J

В результате применения этой методики получаем оценку m 1 ( H ) которая при H = H min также равна 3. Значит, можно выдвинуть предположение, что данная оценка достижима при некотором H , ненамного большим, чем H min .

Однако применение алгоритма FFD при разных H позволило добиться значения k = 3 только при H = 384,3, при этом длительность работы трех используемых ТС составила 327,1; 295,9 и 384,3 мин, соответственно. Т.е. загрузка единиц ТС далека от равномерной. Это означает, что надо подобрать более совершенный алгоритм.

Несложно заметить, что распределение объектов по контейнерам зависит от очередности их рассмотрения. В алгоритме FFD в качестве такой очередности принята упорядоченность по убыванию размеров, хотя строго обоснования такой эвристики нет. Можно ожидать, что проверив несколько вариантов упорядочения, и применив при каждом из них алгоритм FF, мы сможем найти лучшее распределение объектов.

Для генерации различных упорядоченностей можно воспользоваться различными «экономичными» алгоритмами из [18 – 20], в котором каждое упорядочение отличается от предыдущего перестановкой всего двух элементов. Вот как выглядит набор таких перестановок из трех объектов

1 2 3

1 3 2

3 1 2

3 2 1

2 3 1

2 1 3

Помимо экономичности в смысле затрат времени, этот алгоритм при неполном количестве перестановок позволяет варьировать достаточно много элементов набора. Это позволяет надеяться, что для получения оптимальной расстановки не потребуется рассматривать все комбинации, а будет достаточно ограничиться их небольшой частью. Назовем этот алгоритм «First fitted with reordering (FFR)» – «первый подходящий с переупорядочением».

Кроме того, для контроля оптимальности полученного решения можно использовать оценку m 1 при выбранном H , и при совпадении текущего количества контейнеров с этой оценкой можно быть уверенным, что найдено оптимальное решение.

Описанный алгоритм был проверен на примере при нескольких значениях H . Наилучший результат был получен при Н = 338. При n = 10 общее число упорядочений составляет 10! = 3628800. Данный же результат был получен после применения r = 400 вариантов перестановок, примерно за 1,5 секунды. Он приведен в таблице 4. Значение m 1 (338) также получилось равным 3. Это означает, что при H = 338 получить меньшее число контейнеров невозможно никаким алгоритмом и полученное решение оптимально.

Таблица 4.

Результаты расчета по алгоритму «первый подходящий с переупорядочением»

Table 4.

Calculation results by the "first fit with reordering" algorithm

ТС vehicle	Продолжительности составляющих маршрутов, мин Duration of component routes, min	Суммарное время, мин Total time, min
1	128,1 85,2 74,8 48,6	336,7
2	161,8 94,4 76,8	333
3	118,5 134,5 84,6	337,6

Общее время выполнения заказа составит 337,6 минуты, или 5 часов 38 минут. Загрузка ТС близка к равномерной. Выигрыш по времени по сравнению с первоначальным вариантом составил 2,984 раза, при этом число единиц ТС увеличилось в 3 раза. Практически, достигнут идеальный вариант.

Обсуждение

Предлагается следующая методика применения двух приближенных алгоритмов FFD и FFR.

• 1.    После построения системы кольцевых маршрутов, исходя из условий развозки и имеющихся ресурсов, определяем наиболее приемлемое целевое количество k единиц ТС.

• 2.    С помощью оценки m 1 определяем теоретическое значение H min , при котором выбранное количество k ТС может быть достижимо.

• 3.    Постепенно увеличивая значение H ≥ H min , применяем алгоритм FFD, как наиболее быстродействующий, для получения распределения ТС по маршрутам.

• 4.    Если достигнутое распределение нас устраивает в смысле равномерности загрузки ТС, то его принимаем за окончательное решение.

• 5.    В противном случае аналогичным образом используем алгоритм FFR. Число упорядочений, в зависимости от значения n , выбираем в диапазоне 1000 ≤ r ≤ 10000.

• 6.    Обозначим H * – минимальное значение H , при котором выбранное число контейнеров k находится каким либо из примененных алгоритмов. Для найденного значения H * вычисляем оценку m 1 ( H *). Если m 1 ( H *) = k , то убеждаемся в нахождении оптимального решения. В противном случае делаем вывод, что с помощью данной методики оптимальное решение найти невозможно, и при приемлемом показателе равномерности загрузки ТС удовлетворяемся полученным распределением ТС по маршрутам.

Отметим, что наряду с классической задачей об упаковке существует другая задача, в которой требуется упаковать не все объекты в минимальное число контейнеров, а максимальное число объектов в имеющиеся контейнеры [17]. В отношении ее названия в литературе нет однозначного мнения. Иногда ее называют обратной задачей об упаковке в контейнеры. Однако если сопоставить постановки данной задачи и предлагаемой в работе с классической задачей упаковки, то станет ясно, что предлагаемая задача в полной мере соответствует термину «обратная задача упаковки» в отличии от задачи из [17].

Заключение

• 1.    Предложен и проверен на тестовых примерах метод повышения эффективности использования комплекса из нескольких транспортных средств при развозке грузов потребителям.

• 2.    Разработан оригинальный приближенный алгоритм FFR решения известной NP -трудной задачи «Упаковка в контейнеры».

• 3.    Разработана новая методика решения

задачи развозки грузов потребителям, основанная на сочетании двух приближенных алгоритмов ее решения и контроля оптимальности найденного числа единиц ТС.