Методы поиска медианы Кемени для нестрогих и частичных упорядочений альтернатив

Роль информационной поддержки принятия эффективных по заданным критериям решений в различных сферах деятельности общества и государства неуклонно возрастает.

В современном мире моделирование процессов, лежащих в основе принятия решений, является одной из наиболее актуальных задач всех сфер человеческой деятельности [1–5].

Современная методология выбора альтернатив предполагает, что выбор обоснованного решения наступает в момент окончания анализа и обобщения поступающей информации и достижения некоторого порогового значения величины критерия принятия решения. Необходимо отметить, что информация в этом контексте, как правило, означает любые изменения в центральной нервной системе, которые преобразуют восприятие и познание в действие [6].

Традиционно такие модели применяют в психологических исследованиях, включающих варианты бинарного выбора, один из которых «правильный», а другой - «неправильный» в рамках конкретной решаемой задачи [7] для описания ситуаций выбора в азартных играх [2, 8].

В качестве примера в исследовании [9] данный подход был расширен до трех (и более) альтернативных вариантов выбора.

Следует отметить, что некоторые из разработанных моделей позволяют одновременно учитывать все три так называемых контекстных явления: эффект притяжения, эффект сходства и эффект компромисса [10].

Необходимо отметить, что в настоящее время актуальным является обоснование выбора вариантов решений многокритериальных задач в сфере планирования и управления из существующего множества альтернатив с использованием экспертных оценок.

Приближенный метод поиска медианы Кемени для нестрогих предпочтений альтернатив

Рассмотрим построение итогового множества в некотором смысле лучших вариантов из имеющегося конечного множества альтернатив X, состоящего из m вариантов, оцениваемое группой N экспертов. Материалы статья являются логичным продолжением идеи, высказанной в рамках Международной научной конференции «Математические методы в технике и технологиях - ММТТ» в Воронежском государственном техническом университете [11].

В рамках решения сформулированной задачи осуществляют многокритериальный выбор путем сужения исходного множества недоминируемых альтернатив для их дальнейшего более детального анализа или выбор альтернативы из предлагаемого набора X [12].

Известно, что при сужении исходного множества недоминируемых альтернатив результирующее предпочтение лица, принимающего решение (ЛПР), или экспертов представляет собой конусное бинарное отношение типа частичного порядка в пространстве критериев [13], при выборе альтернативы из предлагаемого набора решение представляет функцию ценности в пространстве критериев или линейного порядка на множестве X [12].

В теории экспертных оценок показана важная роль расстояния и медианы Кемени. В исследовании рассматривали задачу коллективного выбора второго типа в соответствии с процедурой, описанной в [14]. Необходимо отметить, что в настоящее время «медиана Кемени» является единственным строгим ранжирующим нейтральным, согласованным и кондорсетовым правилом коллективного выбора; удовлетворяет принципу выбора Кондорсе, не приводя к одноименному парадоксу; удовлетворяет четырем из пяти условий Эрроу [15].

Таким образом, возможно заключить, что медиане Кемени соответствуют самые корректные результирующие отношения.

Следует, однако, отметить недостатки как самого подхода к итоговому ранжированию в виде медианы, так и вычислительных алгоритмов ее поиска. Так, исследования [16, 17], проведенные авторами настоящей работы, показали, что при интерпретации экспертных оценок в виде случайных величин метод медианы Кемени для тестовых примеров с меньшей вероятностью находит истинное упорядочение, чем, например, процедуры Борда и Коупленда. Предлагаемый в [15] метод ветвей и границ позволяет найти итоговое строгое упорядочение за относительно небольшое число итераций. Однако необходимо учесть, что при значительном разбросе мнений экспертов велика вероятность того события, при котором найденное точным алгоритмом решение представляет собой «центр бублика» [18].

Иными словами, найденный вариант итогового упорядочения далек от всех экспертных ранжирований данного профиля и ему не близко ничье экспертное мнение. Среди приближенных методов поиска медианы Кемени следует отметить серию из 7 эвристических алгоритмов, предложенных В.Н. Жихаревым [19].

В пространстве перестановок, снабженного метрикой Кемени, строится система шаров некоторого радиуса R с центрами в точках (перестановках), совпадающими с элементами профиля { P i } экспертного ранжирования. Объединение таких шаров называется R -окрестностью множества { P i }. Постепенно увеличивая значение R и перебирая различными способами точки получающихся R -окрестностей, строится последовательность псевдомедиан Кемени для построенных множеств. Стабилизированная точка последовательности считается решением задачи итогового ранжирования. На наш взгляд, при сильном расхождении мнений экспертов для поиска удовлетворительного итогового упорядочения придется строить окрестность весьма большого значения R , что приведет к необходимости перебора значительного числа точек окрестности, сопоставимом с множеством всех возможных упорядочений [11].

Необходимо отметить, что спорным моментом метода медианы Кемени является обоснованность его применения при наличии эквивалентных или несравнимых альтернатив по В.Д. Ногину [13].

В этих условиях вместо навязывания решения в виде строгого упорядочения более логичным является поиск решения в виде нестрогого бинарного отношения. Так, например, пусть в полученном нестрогом решении оказалось x _i x _j . Скорее всего, это означает, что существуют две оптимальные строгие ранжировки с упорядочениями x i^ xj- и xj-^x i соответственно. Однако при больших предъявлениях нет возможности найти все итоговые упорядочения, и тогда факт одинаковой предпочтительности x i и x j не проявится.

Нестрогость итогового упорядочения может повлечь наличие в итоговом выборе нескольких одинаковых по предпочтению альтернатив. Фактически это будет означать недостаточную избирательную способность применяемого метода. В этом случае для принятия справедливого решения следует подвергнуть выбранные альтернативы более детальному анализу, что при получении строгой ранжировки сделано не будет.

Пары несравнимых альтернатив в графе соответствующего бинарного отношения должны быть изображены в виде изолированных вершин [20].

Для аналитического представления экспертных упорядочений авторы метода [14] предлагают использовать (-1, 0, 1) - матрицы, в которых полагают

1, если ( x i , X j ) е P

A ij ='

0, если x i эквивалентен x j .

- 1, если ( X j , x i ) е P

Там же показано, что для корректного представления отношение предпочтения P в виде матрицы (1) для любых i, j, k должны выполняться три условия:

• I)    A ij = +1, 0 или -1;

• ii)    A ij = — A ji ;

• III)    если A ij >  0 и A j_k >  0, то A i_k >  0, причем A i_k = 0, только если A ij = A j_k = 0.

Условие III) эквивалентно требованию транзитивности P .

В представлении (1) не предусмотрен случай отсутствия отношения P между парой альтернатив. Это означает, что (1) предназначено лишь для связных транзитивных бинарных отношений.

В [20] приведено итоговое упорядочение сроков нововведений с помощью медианы Кемени для прогнозирования в космических технологиях. Для учета наличия неоцененных альтернатив «…было введено понятие ранжировки (раньше–позже) технологических нововведений. … Для событий, которые не упоминались некоторыми экспертами, принималось, что технологическое нововведение может произойти в любой момент в течение века. Для них строка в матрице отношений заполнялась нулями». Для выполнения условия II) нулями заполнялся и столбец. Такое заполнение фактически означает, что неоцененные альтернативы считают эквивалентными всем остальным альтернативам в экспертном ранжировании.

Однако при заполнении только строки и столбца нарушается условие III), а для его выполнения пришлось бы заполнить нулями всю матрицу. Действительно, при наличии транзитивности существование альтернативы, эквивалентной всем остальным вариантам, означает эквивалентность всех альтернатив предъявления. Очевидно, такой подход не является корректным и может привести к противоречию.

В этих условиях наиболее подходящим типом итогового упорядочения является, по нашему мнению, полное транзитивное отношение. Известно, что оно также обладает свойством рефлексивности и негатранзитивности. В разных источниках его именуют нестрогим слабым порядком или линейным квазипорядком. Именно эти свойства обеспечат отсутствие в итоговом упорядочении несравнимых альтернатив и противоречивых (нетранзитивных) предпочтений, присутствие которых сделало бы всю процедуру коллективного выбора бессмысленной. Наличие же в решении эквивалентных альтернатив не сведет результат на нет, а лишь укажет на необходимость дальнейших более тщательных исследований, значительно сузив при этом область поисков.

Исходя из рассмотренных выше примеров, возможно предположить, что в общем случае в качестве исходных упорядочений применимы использоваться следующие их виды:

• а)    кластеризованная ранжировка [18] - полное транзитивное отношение (нестрогий слабый порядок или линейный квазипорядок);

• б)    рефлексивное транзитивное бинарное отношение (квазипорядок или нестрогое частичное предпочтение); при этом предполагается, что соответствующий этому отношению граф является слабо связным т. е. не распадается на отдельные компоненты;

• в)    рефлексивное транзитивное бинарное отношение, но предполагается, что соответствующий этому отношению граф не является слабо связным, т. е. распадается на отдельные компо-

• ненты; в частном случае в исходных упорядочениях могут присутствовать неоцененные альтернативы, т. е. некоторые вершины графа изолированы.

В случае а) результирующее упорядочение принадлежит тому же пространству, что и исходные. В случаях б) и в) пространства исходных и результирующего упорядочения различаются. В общем случае в исходном профиле могут одновременно присутствовать все указанные виды упорядочений.

В данной работе предлагаются точный (переборный) и приближенный алгоритмы нахождения такого решения, которые пригодны для всех описанных случаев экспертных предпочтений, и, на наш взгляд, лишены большинства перечисленных недостатков.

Описание точного алгоритма

Расстояние Кемени удобно вычислять по матричному представлению исходных упорядочений. Авторы метода [14] предлагают для этого использовать матрицы (1). Однако при таком обозначении невозможно корректно представить отношения, содержащие несравнимые альтернативы, или такие, которые эксперты не смогли оценить. Поэтому более обоснованной является традиционная кодировка связей между альтернативами с помощью матрицы смежности, принятая в теории графов:

• 1,    если ( X; , x, ) g P A -L         .

• 0, иначе

В обозначениях (1) 0-матрица является представлением случая эквивалентности всех альтернатив ранжирования. В кодировке (2) ее аналогом следует считать матрицу, состоящую из единиц.

Доказательство справедливости вычислительной формулы для метрики Кемени [14] в представлении (2) почти буквально повторяет аналогичное доказательство для представления (1). Отличие появляется только в лемме 2 при рассмотрении начального пункта индукции для матриц размерности n = 2. Единственная разница в формулах состоит в том, что для достижения минимального расстояния, равного 1, не надо делить сумму на 2, поскольку матрица (2), в отличие от (1), не является кососимметричной. Таким образом, если каждое упорядочение P задано в матричной форме (2), то расстояние от одного упорядочения, представленного матрицей A, до другого упорядочения, представленного матрицей B , вычисляется по формуле

d ( A,B ) = 3 A j - B_y\ .                                (3)

• ¹ ,    j

Пусть { P i } - профиль экспертных упорядочений множества X . Рассмотрим некоторое множество Л нестрогих упорядочений элементов множества X . Каждому упорядочению X g Л приписывается числовая оценка $ ( X ), характеризующая степень близости X ко всему множеству упорядочений из профиля { P i }. Числа $ ( X ) определяются следующим образом:

$ ( X ) = 3 d ( A ^{( Я )}, B ^{( 1} ) ) ,                                      (4)

i где A(Я) - матрица упорядочения X GЛ, B(1) - матрица упорядочения Pi g{Pi}. Результирующее упорядочение X * g Л выбирается из условия минимума $ (Я). Если Л является подмножеством множества всех нестрогих упорядочений, то в [20] для X* предлагается термин «псевдомедиана».

Алгоритм точного нахождения медианы Кемени при нестрогих упорядочениях имеет вычислительную сложность выше экспоненциальной, поэтому для организации выполнимого алгоритма важно максимально исключить генерацию «лишних» элементов, обусловленных повторением уже рассмотренных вариантов. Предлагаемый алгоритм состоит из двух циклов.

Во внешнем цикле в базовом наборе {1,..., т} номеров альтернатив выделяются возможные классы эквивалентности. Число вариантов таких классов определяется числами Стирлинга 2-го рода: S ( т , k ), к = 0,..., т . Во внутреннем цикле перебираются все к ! перестановок сформированных классов. Отсюда число возможных вариантов итогового упорядочения составляет

M = £ k ! S ( т , к ).

к = 0

Для реализации внешнего цикла предлагается воспользоваться известным алгоритмом разбиения множества [21]. Для реализации внутреннего цикла предлагается быстрый алгоритм генерации перестановок, в котором каждый следующий вариант получается из предыдущего инверсией пары соседних элементов [22].

Пример 1. Исходный профиль состоит из двух строгих упорядочений: {( A^B^C ), ( A^C^B )}. Для m = 3 существует 5 вариантов разбиений c выделением классов эквивалентности:

[ A-B-C ], ([ A~B ]> C ], ( A^B^C ), ( A^B^C ), ([ A-C ]> B ].

Теперь, считая каждый класс эквивалентности отдельным неделимым элементом, переберем все упорядочения полученных разбиений. Всего получаем 13 вариантов нестрогих упорядочений. Из них 3 варианта имеют наименьшее значение £ ( X ) = 2: ( A^B^C ), ( A^C^B ), ( A ^ [ B - C ]) . Они и являются решением задачи получения коллективного нестрогого упорядочения.

Пример 2. Исходный профиль содержит 3 частичных нестрогих упорядочения {(C^D, A Ч B-E ]), ( A^ [ B-E ], A- C- D ) ( A ^[ B E ]> D , A^ C )} Для поиска решения надо рассмотреть 541 вариант упорядочений. Решением являются две кластеризованные ранжировки следующего вида:

( A ^[ B E ] >C>D ) и ( A^C >[ B-E ]> D ) .

Для обоих решений сумма расстояний до элементов исходного профиля равна 13.

Описание приближенного алгоритма нахождения медианы Кемени

Разработан приближенный алгоритм типа локальных вариаций для перебора вариантов, близких к исходным упорядочениям согласно метрике (3).

Введем следующее понятие: к-вариацией произвольного упорядочения, представленного матрицей вида (2), назовем упорядочение, полученное инверсией к элементов матрицы (2) и последующим преобразованием к виду а). Пусть, например, имеем упорядочение ( A >- [ B-E ], A^C^D ), матрица которого имеет вид:

( 1   1

A = 0

( 0  1

1    1    1

0  01

1   10

0  10

0  0  1

Инвертируем два элемента матрицы A ₃₅ и A ₅₃, добавив тем самым в исходное упорядочение предпочтения C^ E и De E . Полученное таким образом отношение, однако, не является транзитивным. Поэтому построим для него транзитивное замыкание.

В результате получим отношение ( AeCe D >- [ B - E ]) с матрицей

(1 1 1 1 1 > 0 1 0 0 1 A(1) = 0 1 1 1 1 0 1 0 1 1 < 0 1 0 0 1; являющееся 2-вариацией исходного отношения.

Предлагаемый приближенный алгоритм нахождения медианы Кемени состоит из двух эта- пов.

Этап 1. Задается начальное значение параметра метода к ₀ . Для упорядочений входного профиля { P i } строится окрестность Л ⁽⁰⁾, элементами которой являются их к -вариации, 1 <  к <  к ₀. Если во входном профиле присутствуют только упорядочения вида а), то этап 1 опускается и полагается Л ⁽⁰⁾ = { P i }.

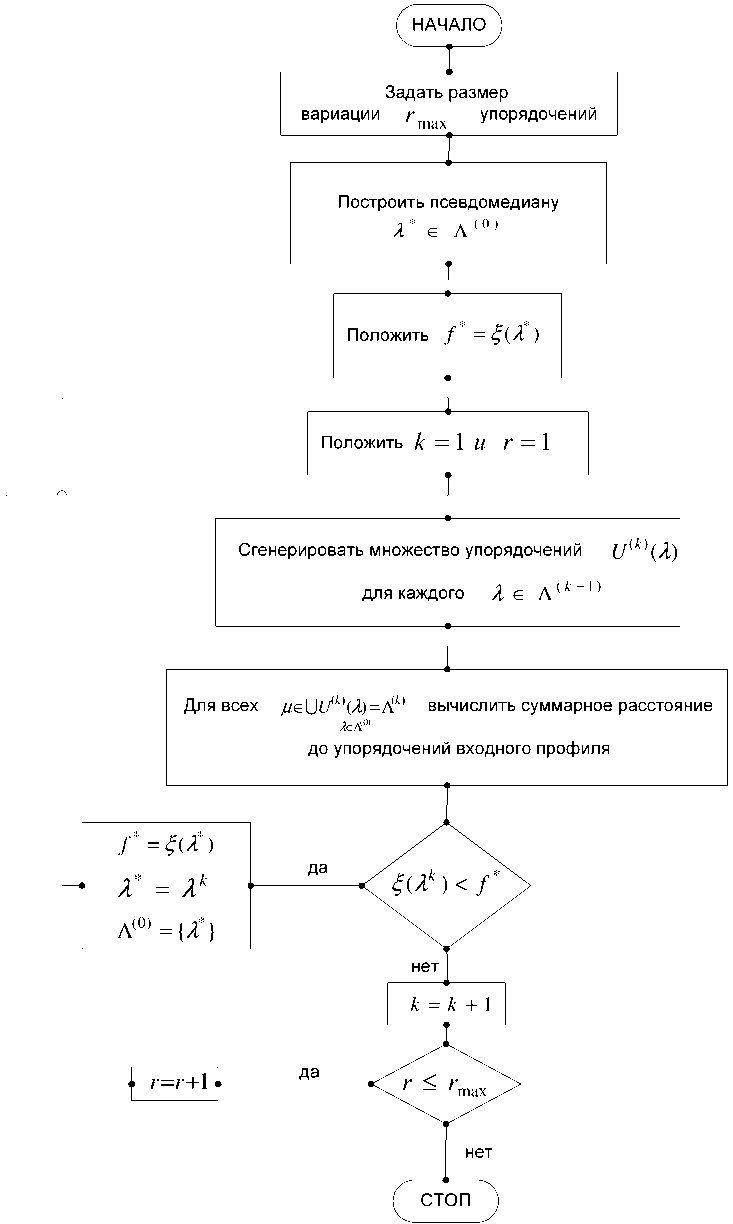
Схема алгоритма второго этапа приближенного алгоритма нахождения медианы Кемени

Этап 2. Строится система новых шаров, для которых все Л еЛ ⁽⁰⁾ рассматриваются как центры. Среди сгенерированных упорядочений ищутся элементы, наименее удаленные от профиля в смысле метрики (3). Из них формируется новое множество центров, и этап повторяется до момента прекращения улучшения сгенерированных решений.

На рисунке представлена укрупнённая схема алгоритма второго этапа.

Формирование k -вариаций возможно с использованием алгоритма генерации k -подмножеств [21], проверка транзитивности осуществима посредством алгоритма Уоршалла [22], а связность отношения проверяется с помощью анализа на слабую связность ориентированного графа упорядочения [22].

Особенности численной реализации приближенного алгоритма нахождения медианы Кемени

Решим с помощью описанного алгоритма задачу примера 2.

На первом этапе получим окрестности всех упорядочений входного профиля. При этом ограничимся варьированием не более двух элементов соответствующих матриц и оставляя в наборе Л ⁽⁰⁾ упорядочения, отстоящие от центра окрестности не более чем на 8.

Например, варьируя по одному элементу матрицы упорядочения, получим следующие ранжирования. Для первого упорядочения были получены 1-вариации: (C >- A >- [ B ~ E ]) (в исходное упорядочение добавилось предпочтение ( D^ A ); A^ [ B- E ] >- C> D (добавилось B > C ).

Для второго упорядочения получены:  [ A-B-E ]>- C^D , (добавилось  ( B^D ));

[ A - C - D ] >- [ B - E ] (добавилось ( D >- A) ) и т. д.

Окончательно был получен набор упорядочений, состоящий из 64 вариантов (вместо 541 при полном переборе). Среди них на втором этапе найдены все упорядочения с наименьшей суммой расстояний от элементов профиля. В результате получены оба решения, найденные ранее с помощью полного перебора.

Выводы

Таким образом, предложен вариант обоснования выбора вариантов решений многокритериальных задач в сфере планирования и управления из существующего множества альтернатив с использованием экспертных оценок.

В рамках современной методологии выбора альтернатив предложены два алгоритма поиска медианы Кемени при наличии нестрогих и частичных упорядочений альтернатив в исходном профиле, а также при наличии альтернатив, не оцененных экспертами. Показано, что приближенный алгоритм находит решение значительно быстрее точного алгоритма.

Показано, что разработанный алгоритм гарантирует отсутствие эффекта «центра бублика», то есть при наличии нескольких решений алгоритм позволяет найти вариант альтернативы, достаточно близкий к какому-нибудь экспертному упорядочению.

Следует отметить, что при формировании исходного профиля корректно кодируются неоцененные альтернативы.