Методы проверки транзитивности индивидуальных экспертных предпочтений

Следует отметить, что при формировании коллективного выбора требование транзитивности профиля предпочтений может нарушаться. Это считается нормальным, т.к. является следствием несовпадения индивидуальных мнений экспертов. Однако в индивидуальном предпочтении оно недопустимо. Поэтому, если мы хотим иметь теорию, в рамках которой осуществляется «наилучший» выбор, то индивидуальные предпочтения должны удовлетворять аксиоме транзитивности, в противном случае вполне может существовать множество решений, выбрать наилучшее из которых невозможно.

В работе [1] вопросу проверки нетранзи-тивности индивидуальных предпочтений уделено достаточно внимания. В частности, показана связь между нетранзитивностью и пустотой относительной внутренности области допустимых коэффициентов постулируемой функции обобщённого критерия. В настоящей же работе предлагаются более универсальные подходы (далее I и II), не связанные с допущением о существовании какого-либо обобщённого критерия, а использующие исходную информацию в виде матрицы парных индивидуальных сравнений альтернатив выборки.

I). Из теории бинарных отношений известно следующее: если бинарное отношение антирефлексивно и транзитивно, то оно ациклично. Обозначим свойства антирефлексивности, транзитивности и ацикличности буквами A , B , C , соответственно. Тогда данное свойство можно символически представить в виде следующей формулы алгебры высказываний:

A л B ^ C, или в приведённой формеЛ

• —- A v —- B v C .

К последней формуле приводится также выражение:

• — C л A ^ — B , которое означает нетранзитивность циклического и антирефлексивного отношения.

Если в индивидуальных предпочтениях исключить повторения альтернатив выборки, то антирефлексивность отношения предпочтения достигается автоматически. Следовательно, при наличии антирефлексивности транзитивность эквивалентна ацикличности.

Очевидно, если C[r] - структурная матрица предпочтений r-го эксперта, то - C[r] T представляет собой матрицу инциденций графа G, соответствующего отношению индивидyaльного предпочтения. Если ранжирование проводилось на порядковой шкале, то этот граф является турниром (турнир - полный ориентированный граф). Если этот граф содержит контур, то, очевидно, индивидуальное предпочтение циклично, т.е. не удовлетворяет выдвинутым требованиям.

Существует несколько методов проверки наличия контура в графе. Изложим один, ос-ʜoʙaʜʜый ʜa cледующих очевидных свойстʙax графа:

• -    в бесконтурном графе существует хотя бы одна вершина, в которую не заходит ни одна дуга;

• -    такая вершина не может принадлежать контуру;

• -    если из графа исключить такую вершину и инцидентные ей дуги, то имеющийся в графе контур останется без изменения.

Таким образом, алгоритм состоит в последовательном исключении из графа вершин, в которые не заходит ни одна дуга. Если на очередном шаге таких вершин не окажется, то граф содержит контур. Если из графа будут удалены все вершины, то граф не содержит контуров.

Предлагается текст программы на входном языке системы Matlab, использующей матрицу инциденций.

function P=Kontur(C1)

• %    Поиск контуров в орграфе. С1 - мат-рицa cмежности

C=-C1;

Y=true;

while (~isempty(C))& Y [nn,mm]=size(C);

Y=false;

foru=1:nn ifall(C(u,:)>=0) % Вершина u не имеет входящей дуги

Y=true;

h=find(C(u,:)==1);

C(:,h)=[];

C(u,:)=[];

break;

end end end if Y display(,КОНТУРОВНЕТ,);

P=false;

else display(,КОНТУРЕСТЬ,);

P=true;

End

Bычислительʜaя сложность aлгоритмa оценивается величиной O ( n • m ), где n , m - число вершин и дуг графа, соответственно, т.к.

ВестникВГУИТ, №2, 2014

необходимо однократно просмотреть все эле- менты матрицы инциденций.

Рассмотрим пример графа, содержащего замкнутый контур (рисунок 1):

Рисунок 1. Граф, содержащий замкнутый контур

Матрица инциденций этого графа имеет вид:

" 0   1    0   0  -1   1    0   0   0   0

0   0   0   0    0   0   0   1  -11

0   0   0   1   1   0   0  -1   00

0   0   0   0   0   0   1   0   0-1

D =

0   0   0   0   0  -1   0   0   10

0   0   1   0   0   0  -1   0   00

1 00 -1 000000

• -1  -1  -1   0   0   0   0   0   00

Вызываем программу:

P=Kontur(D);

ans = КОНТУР ЕСТЬ

Теперь рассмотрим пример графа без контуров (рисунок 2):

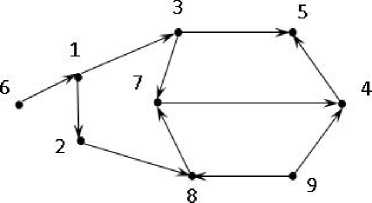
Рисунок 2. Граф без замкнутых контуров

	Г 1	-1	-1	0	0	0	0	0	0	0	0 "
	0	0	1	0	0	-1	0	0	0	0	0
	0	1	0	-1	-1	0	0	0	0	0	0
	0	0	0	0	0	0	0	1	-1	0	1
F =	0	0	0	0	1	0	0	0	1	0	0
	-1	0	0	0	0	0	0	0	0	0	0
	0	0	0	1	0	0	1	-1	0	0	0
	0	0	0	0	0	1	-1	0	0	1	0
	L 0	0	0	0	0	0	0	0	0	-1	-1

P1=Kontur(F);

ans = КОНТУРОВ НЕТ.

• II). Во многом проблема нарушения транзитивности индивидуального экспертного ранжирования связана с тем, что эксперт, сравнивая альтернативы попарно, вообще говоря, не обязан думать о том, как соотносятся эти альтернативы со всеми остальными. При этом велика вероятность нарушения согласованности предпочтений, которые делают бесполезной дальнейшую обработку результатов экспертизы.

Для решения указанной проблемы в [2] используется следующий алгоритм (назовём его «Алгоритм 1»):

• 1) . На основе указанных r -ым экспертом пар предпочтений и эквивалентности строится вспомогательная матрица Y [ r ] (размерности n x n , где n - количество альтернатив выборки), по которой осуществляется предварительная оценка результатов его опроса . Значения Y_{i j} ,

устанавливающие отношения между парой альтернатив( (Ai, Aj), причём i ^ j) опреде- ляются следующим образом:

Y = ^ ij

1, если

- 1, если

0, если

A i ^ A j ;

A j ^ A i ; (1) A i ~ A j .

Далее в ходе проведения экспертного опроса, с учётом требований достижения тран- зитивности упорядочения альтернатив, в матрицу Y добавляются новые соотношения между объектами согласно (1) и правилам, приведённым в таблице 1, где:

i = 1, n , j 1 = 1, n , j 2 = 1, n .

Таблица 1

Правила, устанавливающие отношения между альтернативами согласно требованию достиже-ниятранзитивности экспертных предпочтений при ранжировании выборки на порядковой шкале

Y. i j 1	Y. i j 2	Y . j 1 j 2
0	-1	-1
1	-1	-1
0	1	1
-1	1	1
1	0	-1
-1	0	1
0	0	0
-1	-1	0
1	1	0

• 2) . В том случае, если добавляемое в матрицу Y соотношение уже имеет значение, полученное на предыдущих этапах построения вспомогательной матрицы, производится генерация уведомления о нарушении условия транзитивности экспертного ранжирования;

• 3) . Экспертное упорядочение будет считаться полным, если все Y ij ( i * j ) будут заполнены согласно правилам (таблица 1).

В результате проведения экспертного опроса должны быть сформированы матрицы С [ r ], отражающие структуру предпочтений каждого г- гоэксперта. Причём, в идеале такие матрицы должны содержать всевозможные предпочтения между всеми парами альтернатив выборки (далее такие структурные матрицы будем называть - «полными»).

Таким образом, помимо выполнения условия транзитивности, необходимо чтобы построенные матрицы С [ r ] отражали всевозможные отношения между всеми парами альтернатив из исходной выборки.

Применение Алгоритма 1 корректно решает обе вышеприведённые проблемы, если упорядочение альтернатив проводится экспертами с использованием порядковой шкалы. Однако, если количество альтернатив достаточно велико и их ранжирование производится экспертами на лингвистической шкале [3, 4], более сильной по сравнению с порядковой, то построение полных С [ r ] существенно усложняется. (Поскольку название «лингвистическая шкала» может навести на неверную мысль об использовании лингвистической переменной Л. А. Заде, то в дальнейшем будем называть её разностноклассификационной или РК-шкалой ).

Вследствие чего, нами предложена модификация Алгоритма 1 (назовём её «Алгоритм 2»), которая позволяет осуществлять проверку условия транзитивности экспертных предпочтений и формировать полные структурные матрицы всевозможных предпочтений С [ r ] при упорядочении альтернатив на РК-шкале. Применение РК-шкалы позволяет значительно повысить точность статистических оценок полезностей альтернатив и состоит в следующем.

Пусть для пары альтернатив ( A i , A j ) эксперт способен оценить величину разности в их полезности. На основании такой оценки пара должна быть отнесена к одному из классов Q ₀, Q 1 ,..., Q s каждый из которых характеризуется определенной степенью различия в полезности A i и A j . Например, принадлежность ( A i ,A j ) е Q ₀ будем соотносить с ситуацией неразличимости по полезности A i и A j . Следующий класс Q 1 соответствует уровню «малое» превосходство A i над A j и т. д. по порядку возрастания силы превосходства.

Алгоритм 2 при упорядочении выборки на РК-шкале состоит в следующем:

• 1) . На основе указанных r -ым экспертом пар предпочтений строится вспомогательная

матрица Y[r]. Значения матрицы Yij, устанав ливающие отношения между парой альтерна тив ((Ai, Aj) , причём i * j) определяются следующим образом:

	' 2, 1,	если если	( A , , A j ) g Q 2 ; ( A„ A ) g Q 1 ;
Yj =-	0,	если	( A , , A j ) g Q o ; (2)
	- 1,	если	( A j , A , ) g Q 1 ;
	- 2,	если	( A , A , ) g Q 2 .

Далее с учётом требований достижения транзитивности предпочтений в Y добавляются новые соотношения между объектами согласно (2) и правилам, приведённым в таблице 2, где i = 1, n, j 1 = 1, n, j2 = 1, n.

Таблица 2

Правила, устанавливающие отношения между альтернативами согласно требованию достижения транзитивности экспертных предпочтений при ранжировании выборки на РК-шкале

У . ij 1	У . ij 2	y.. j 1 j 2
2	2	0
2	1	-1
2	0	-2
2	-1	-2
2	-2	-2
1	1	0
1	2	1
1	0	-1
1	-1	-2
1	-2	-2
0	0	0
0	2	2
0	1	1
0	-1	-1
0	-2	-2
-1	-1	0
-1	2	2
-1	1	2
-1	0	1
-1	-2	-1
-2	-2	0
-2	2	2
-2	1	2
-2	0	2
-2	-1	1

• 2) . В том случае, если добавляемое в матрицу Y соотношение уже имеет значение, полученное на предыдущих этапах построения вспомогательной матрицы, производится генерация уведомления о нарушении условия транзитивности экспертного ранжирования;

• 3) . Экспертное упорядочение будет считаться полным, если все Y i j ( i * j ) будут заполнены согласно правилам (таблица 2).

• 4) . После окончания опроса эксперта на основе матрицы Y формируется полная структурная матрица его всевозможных предпочтений С [ r ].

Таким образом, идея Алгоритма 2 состоит в том, чтобы на основе вспомогательных матриц Y [ r ] обеспечить не только проверку индивидуальных экспертных предпочтений на транзитивность, но и по окончании опроса экспертов сформировать полные матрицы С [ r ] всевозможных предпочтений между всеми парами альтернатив выборки.

Предлагается текс функции на входном языке системы Matlab, осуществляющей построение полной матрицы С [ r ] на основе вспомогательной матрицы Y [ r ].

Предположим, что изначально все элементы матрицы Y [ r ] имеют значение k, отличное от значений, которые может принимать величина Y _i j в выражении (2).

function C=Struct_matr(Y);

% C–полная структурная матрица экспертного упорядочения

M_sum=[];

C=[];

M_sum=sum(Y')-k;

[elem,index]=sort(M_sum,'descend');

C=nchoosek(index,2); % сочетания без повторений

C(:,3)=0;

for j=1:length(C),

C(j,3)=Y(C(j,1),C(j,2));

end

Приведём иллюстрирующий пример работы Алгоритма 2.

• Пр имер 1 . Пусть r -ый эксперт предложил следующее упорядочение пяти альтернатив на РК-шкале:

" ( A i , A 2 ) е Q i ( A 2 , A 3 ) е Q 2 ( A 3 , A 4 ) е Q i

_ ( A 4 , A 5 ) е Q 0

Предположим, что вспомогательная матрица Y [ r ] инициализируется следующим образом:

	" 3	3	3	3	3
	3	3	3	3	3
( r )	3	3	3	3	3
	3	3	3	3	3
	_ 3	3	3	3	3

Далее покажем, как будет изменяться вид матрицы Y[r] с учётом требований дости- жения транзитивности упорядочения альтернатив, при последовательном добавлении экспертом предпочтений из ранжирования (3).

1)	( A i , A 2 ) е Q i
		" 3	1	3	3	3
		-i	3	3	3	3
	Y ( r ) =	3	3	3	3	3
		3	3	3	3	3
		3	3	3	3	3 _
2)	( A 2 , A 3 ) е Q 2
		" 3	1	2	3	3
		-1	3	2	3	3
	Y ( r ) =	-2	-2	3	3	3
		3	3	3	3	3
		_ 3	3	3	3	3
3)	( A 3 , A 4 )	е Q i
		" 3	1	2	2	3
		-1	3	2	2	3
	( r )	-2	-2	3	1	3
		— 2	-2	-1	3	3
		_ 3	3	3	3	3
4) ( A 4, A 5 ) е Q 0 :
		" 3	1	2	2	2
		-1	3	2	2	2
	( r )	-2	-2	3	1	1
		— 2	-2	-1	3	0
		_ -2	-2	-1	0	3

Согласно шагу 3 Алгоритма 2 экспертное упорядочение будет считаться полным.

Затем вызывается вышеприведённая функция «Struct_matr», которая на основе полученной вспомогательной матрицы Y[r] фор- мирует полную структурную матрицу всевозможных предпочтений экспертаС[r]:

C ( r ) ^T

Таким образом, в данной статье приведены алгоритмы, обеспечивающие проверку индивидуальных экспертных предпочтений на непротиворечивость при упорядочении исходной выборки альтернатив на порядковой и разностно-классификационной шкале.

Работа поддержана грантом РФФИ №14-01-00653-А «Разработка и исследование процедур коллективного выбора на необозримом для ЛПР множестве альтернатив».