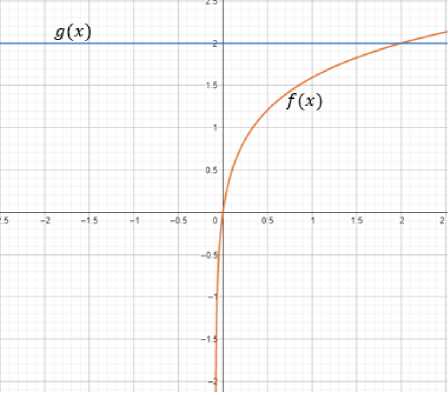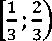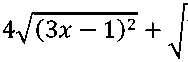Пример 1. Решите неравенство log4(X-5)< .
Решение. Используя свойства логарифмов, представим число справа в виде логариф ма с основанием 4. Тогда неравенство примет вид:
log4(X-5)< log44=log4 2 ⇔ log4(X-5)
Приведем полученные неравенства к равносильной системе
X-5>0,
■X -5<2
X>5,
⇔ ⇔5<X<7.
X<7,
Ответ. X∈(5;7).
Пример 2. Решите неравенство log 1(7-6X)∙log2-Х 4≥1. 9
Решение. Найдем ОДЗ:
7-6 >0,< ,
2-X>0, ⇔ I X<2, ⇒X∈(-∞;1)∪ 1;б) .
2-X≠1;≠1;
Упростим исходное неравенство:
\ log1(7-6X)∙log2-x 3≥1 ⇔ log2-x(7-6X)≥2 ⇔
⇔ log2-X(7-6X)≥log2-X(2-X)2.
При X∈ 1; (1) основание 2-X<1, тогда неравенство равносильно: (7-6X)≤
(2-X)2⇔ X2 +2X-3≥0 ⇔ (X+3)∙(X-1)≥0 ⇔
⇔X∈(-∞;-3] ∪[1;+∞). Учитывая условие (1), получаемX∈ 1; — J.
При X∈(-∞;1) основание 2-X>1, (2-X)2⇔X∈[-3;1]. Учитывая условиеX тогда неравенство равносильно: ∈(-∞;1), получаемX∈[-3;1).
(7-6X)≥
Ответ. X∈
Правую и левую части неравенства рассматриваем как две отдельные функции "У =(X) и "У =(X), их графики строим в одной системе координат и смотрим, какой из графиков располагается выше другого, и на каких промежутках. Оцениваются промежутки следующим образом:
- решениями неравенства / (%) > у (%) являются интервалы, где график функции / (%) не ниже графика функции у (%);
- решениями неравенства / (%) < у (%) являются интервалы, где график функции /(%) не выше графика функции у (%);
Другая особенность – результаты, полученные по графикам. Их можно считать лишь приближенными. Бывает, что определенные по графикам значения корней оказываются точными значениями, в чем дает убедиться проверка подстановкой. В других случаях, есть возможность уточ- нить значения корней до требуемой степени точности, для этого существуют специальные методы уточнения значений корней. В некоторых случаях по графикам невозможно определить количество корней, их значения. В таких ситуациях стоит отказаться от графического метода.
Пример 3. Решить неравенство logз(2% — 4) > logз(14 — %).
Решение. В одной системе координат построим два графика: /(%) = logз(2% — 4) и у (%) = logз (14 — %) (рисунок 1).
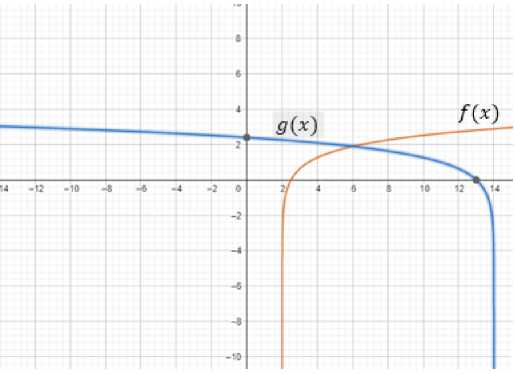
Рис. 1. Графики функций /(%) = logз(2% — 4) и у (%) = logз(14 — %)
По рисунку 1 видно, что абсциссой точки пересечения двух графиков является 6. Так как имеем неравенство /(%) > у (%), тогда выбираем интервал, где график функции / (%) выше графика функции у (%). Получаем интервал (6; 14).
Ответ: х G (6; 14).
Пример 4. Решить неравенство log 5(12% + 1) < 2.
Решение. Рассмотрим две функции: f (%) = log 5(12% + 1) и у (%) =2. Построим графики данных функций в одной прямоугольной системе координат (рис. 2).
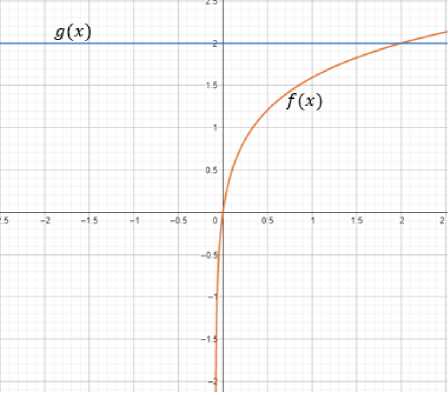
Рис. 2. Графики функций /(%) = log 5(12% + 1) и у (%) =2
Абсцисса точки пересечения двух графиков равна 2. Так как в рассматриваемом примере f(X)≤9(x), тогда решением неравенства являются интервалы, где график функции У(X) не выше графика функции 9(x). По рисунку 2 видно, что промежуток (- ;2] является приближенным решением данного неравенства, так как по рисунку невозможно точно определить к какому значению слева стремиться функция у(x).
Ответ: X∈(- ;2].
задача решается с помощью метода интервалов.
Пример 5. Решить неравенство logI^v9≥-1.
Решение. Всегда решение логарифмического неравенства начинаем с области допустимых значений. Выражение под знаком логарифма должно быть положи-2 — 3% тельным, то есть >0. Это условие обязательно должно выполняться, и к нему мы вернемся. Рассмотрим пока само неравенство. Запишем левую часть как логарифм по основанию 3:
log3 ≥-1. Правую часть тоже можно записать как логарифм по основанию 3, а затем перейти к алгебраическому неравенству:
log3(2-3^
≥log33⇔
X 1
2-3X≥3.
2 — 3%
Видим, что условие >0, то есть ОДЗ, теперь выполняется автоматически. Это уп- рощает решение неравенства.
2-3X-3
≥0⇔
3X-1
≥0
2-3X
Решаем неравенство методом интервалов:

Ответ: X∈
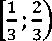
Пример 6. Решить неравенство
log0,2(X2 +6X+8)>log0,2 (5X + 10).
Решение. Найдем ОДЗ:
%2 +6X+8>0, 5X+10>0.
⇔X∈(-2;+∞).
Поскольку основание у нас 0,2<1, то знак неравенства меняем. Получим:
X2 +6X+8<5X+10. Упростим полученное неравенство: X2 +X-2<0. Применим метод интервалов. Корни уравнения X2 +X-2=0: X1=-2; X2=1.
Наносим найденные точки на числовую ось и вычисляем знаки на каждом интервале:

2 1
х∈(-2;1).
Окончательное решение неравенства – пересечение ОДЗ с только что полученным множеством. Получим:
X
---------о--------о---------*--2 1
Ответ: х∈(-2;1).
Неравенство вида logf( ) ^9 (х))V logj( )(ℎ(X)) , в области его допустимых значений, можно заменить равносильным неравенством
(f(X)-1)(g (X)-ℎ(X))V0.
Здесь знак V означает любой из знаков <, >, ≤ или ≥.
Пример 7. Решите неравенство logx+1 (X-1)≥0.
Решение. Найдем область допустимых значений:
X+1>0
X+1≠1 ⇔X>1.
a-1>0
По методу рационализации: на ОДЗ logx+1 (X-1)≥0⇔(X+1-1)·(X-1-1)≥0⇔X·(X-2)≥0.
Так как на ОДЗ X>1, то на ОДЗ последнее неравенство равносильно неравенству:
(X-2)≥0⇔X≥2. С учетом ОДЗ, получим:X∈[2;+∞).
Ответ: X∈[2;+∞).
Рассмотри более сложное неравенство.
Пример 8. Решите неравенство
(X2+3X-10)∙log0,5(X2 -1) log(x2-l)(X+2)≤0.
Решение.
Выпишем ОДЗ неравенства:
(x2-1>0,
I x+2>0, ⇒X∈(-2;-√2) ∪ -√2;-1)∪(1;√2)∪(√2; +∞ .
[%2-1≠1;
Решим неравенство на ОДЗ.
Заметим, что по формуле log a b ∙logb ^=loga c неравенство можно переписать в виде:
(X2 +3X-10)∙log ,(X+2)≤0.
По методу рационализации данное равенство равносильно:
(X2+3X-10)∙(0,5-1)(X+2-1)≤0,
(X+5)(X-2)(X+1)≥0.
Решая данное неравенство методом интервалов, получим:
X∈[-5;-1] ∪[2;+∞).
Пересечем ответ с ОДЗ и получим окончательный ответ
X∈-2; -√2) ∪ -√2; -1)∪[2;+∞).
Ответ: X∈ -2; -√2)∪(-√2;-1) ∪ [2; +∞).
На наш взгляд, данный метод является экономичным по времени, так как легко преобразовать логарифмическое неравенство к нужному рациональному неравенству.
5) Перейдем к методу замены переменных. Суть метода в том, чтобы от неравенства, содержащего в качестве множителей сложные логарифмические выражения, перейти к равносильному ему более простому рациональному неравенству. Данный метод чаще применяется при решении неравенств, содержащих квадрат логарифма и квадрат выражения, в котором содержится логарифм.
Пример 8. Решите неравенство:
(log2^-2log2 Х)2 < 11log2^ -
22 log2X-24.
Решение. Перепишем данное неравенство в виде:
(log2*-2log2 Х)2 - 11(log2^ -2log2^)+24<0.
Применим метод замены переменных. Пусть log2Х-2log2 ^= , тогда имеем равносильное неравенство (равносильными называются неравенства, множества решений которых совпадают):
с2-11t+24<0 ⇔ (t-3)(t-8)<
0, с решением 3<t<8.
Вернемся к переменной :
32log2X<8 ⇔
log2%-2log2X-3>0, log2X-2log2X-8<0.
В результаты замены log2 *^ = приходим к системе неравенств у2 -2У-3>0,
■у2 -2у-8<0,
⇔
(У+1)(У-3)
(У+2)(У-4)
>0,
<0,
⇔
( [у<-1, У>3, -2<у<4.
Обратная замена приводит к системе log2 х<-1, log2Х3, ⇔ log 2 Х>log2 8, ⇔ - L х>8,
-21.
Ответ. X∈ ; ∪(8;16).
\4 2/ v J
5) Рассмотрим метод мажорант (другое название – метод оценок).
Метод мажорант основан на том, что множество значений некоторых функций ограничено. При использовании данного метода нужно выявить точки ограниченности функции, то есть в каких пределах изменяется данная функция, а затем ис-
пользовать эту информацию для решения неравенства.
Основной признак неравенств, в которых нужно применить метод мажорант: имеется смешанное неравенство, то есть в задании присутствуют разнородные функции, например, линейная и логарифмическая.
Пример 9. Решить неравенство: 7 |X 3|∙log2 (6X- X2-7)≥1.
Решение. Преобразуем данное неравенство:
log2 (6X- X2-7)≥ 7|X 3 .
Рассмотрим левую часть получившегося неравенства log2 (6X- X2 -7). Преобразуем подлогарифмическое выражение:
6X- X2-7= -(X2 -6X+9)+2=-(X-3)2 +2.
Получаем, что подлогарифмическое выражение 6X- X2-7≤2. Так как "У =log2 t возрастает при t>0, то:
log2 (6X- X2-7)≤log22⇔ log2 (6X- X2-7)≤1.
Рассмотрим правую часть 7|X 3 | . Известно, что у= 7 f возрастает. Так как | X-3|≥0, то 7|X 3| ≥70⇔ 7|X 3| ≥1.
Получаем, что левая и правая части равны 1. Следовательно, неравенство log2 (6X-л 2-7)≥ 7 t-3 равносильно системе:
log2 (6X- X2-7)=1, 7|X 3|=1.
Решив первое уравнение системы, получаем X=3. Проверим первое уравнение, подставив значение X=3. Получаем верное равенство log2(6∙3-32-7)=1.
Значит, X=3 является решением неравен ства 7 |X 3|∙log2 (6X- X2-7)≥1.
Ответ: X=3.
Пример 10. Решить неравенство:
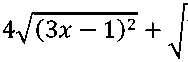
X2 +16log4 X≤4-12X.
Решение.
1. Упростим первый корень неравенства:
4|3X-1|+ log +16log4 X≤4-12X.
2. Заметим, что оба слагаемых в левой части неравенства неотрицательны, следовательно, правая часть также должна быть неотрицательна, то есть 4-12X≥0 ⇔
X < -
.
При этих значениях X подмодульное выражение отрицательно, следовательно, раскрываем модуль с противоположным знаком:
-4(3X-1)+ log22 X2+16log4 X≤4-12X, log22 X2 +16log4 X≤0.
Так как квадратный корень – величина неотрицательная, следовательно, неравенство выполняется, если только левая часть равна нулю [10].
3. Решим уравнение: log2 х2 +
16 log4 X=0. Приведем второй логарифм к основанию 2: log 2 х2 +8log2 =0
Преобразуем первое слагаемое:
log 2 %2 = (log2^)2=(2log2|X|) =
(2 log2 )2 – раскрыли модуль с тем же знаком, так как X>0 по ОДЗ исходного неравенства.
Теперь введем замену переменной: log2 X= (метод замены рассматривался выше). Получим уравнение: 4t2 +8t=0. Решая данное уравнение, получим: t=0 или t=-2. Вернемся к исходной переменной: log2 X=0 или log2 X=-2. От- v 1 „ 1
сюда X=1 илиX=.
Легко проверить, что только число 1
X = является решением исходного неравенства. Так как мы не находили ОДЗ, проверку нужно сделать обязательно.
Ответ: X=.
В работе представлены нестандартные методы решения логарифмических неравенств. Рассмотренные на конкретных примерах способы позволяют значительно облегчить, а в некоторых случаях и ускорить процесс решения неравенств. Примеры подобраны из работ [1-10].
Данная статья может быть использована обучающимися для повторения и систематизации материала по теме «Логарифмические неравенства», а также учителями математики для элективных курсов.