Методы сеточной аппроксимации сложных систем событий

Ввиду большого числа событий в реальных статистических системах, возникает трудность определения состояний, в которых может оказаться система. Один из способов преодоления трудностей подобного рода заключается в отыскании сеточного распределения состояния системы, определенного на введенной сетке и близкого к искомому неизвестному распределению. Матричные модели маркетинга [1] натолкнули на идею методов аппроксимации распределений, аналогичных сеточным методам решения дифференциальных уравнений.

Постановка задачи

Существо сеточного метода состоит в следующем: вместо исходного пространства элементарных событий вводится его сеточный аналог. Эта сеточная модель описывается вероятностями, которые определены только на событиях сетки. Неизвестные распределения, т.е. законы, в соответствии с которыми эволюционирует пространство элементарных событий, заменяется соответствующими сеточными аналогами. В итоге исходная задача заменяется, или, как говорят, аппроксимируется системой сеточных распределений - сеточной схемой. Другими словами, на аппроксимируемое множество событий «набрасывается сетка» с целью попытаться представить, как ведут себя «неизвестные» события из аппроксимируемого множества в пределах «известных ячеек», роль которых будет предоставлено исполнять событиям-терраскам, образующим сетку.

Основные понятия эвентологии и теории вероятностей

Эвентология - новое направление, возникшее в рамках теории вероятностей и изучающее распределение множеств событий, структуры зависимостей множеств событий [2].

Определение 1.1. Вероятностным пространством называется тройка (О, F, Р), где Q -пространство элементарных событий, F - алгебра событий и Р - вероятность, определенная на элементах алгебры F - случайных событиях х, у, ...е F.

Определение 1.2. Конечное множество избранных событий X е F, выбранных из алгебры вероятностного пространства (О, F, Р) и состоящее из 7V = ]x| событий, называется множеством случайных событий.

Определение 1.3. Множество случайных событий X порождает различные наборы так называемых событий-террасок, среди которых есть события-терраски для X с X в форме пересечения: ter(X)= Qx Q^a'^C ■ хеХ

Определение 1.4. Два случайных события х, у е X (х ■£ $, у * 0) называются вложенными, если между ними возможны только два отношения fx, то есть одно из этих событий вложено в другое: х с у или у с х.

Сетка событий, или эвентологическая сетка (Э-сетка)

Начальным этапом построения сеточной схемы является замена исходного пространства элементарных событий некоторой сеткой событий, образующих его разбиение.

Определение 2.1. Эвентологическая сетка (Э-сетка) - это множество ScF непересекаю-щихся случайных событий, выбранных из алгебры F вероятностного пространства (fl, F, Р) и образующих разбиение пространства элементарных событий Q.

Э-сетка 5 (сеточное множество случайных событий S, сеточное эвентологическое распределение множества S) определена тогда и только тогда, когда:

• 1)    выбрано множество S a F непересекающихся случайных событий, образующих разбиение О = У s ;

• 2)    задан набор вероятностей qp) = P(s), s е S.

Для «одномерной» задачи простейшим примером Э-сетки является равновероятное разбиение пространства элементарных событий на N равновероятных событий, вероятность которых равна WN равновероятная Э-сетка). Равновероятные события Э-сетки называются Э-террасками сетки (Э-узлами сетки), а их вероятности называют также Э-шагами сетки. Совокупность Э-террасок образует множество событий, где определены Э-сеточные распределения.

Определение 2.2. Эвентологической сеткой n-го порядка Sⁿ пространства элементарных событий О называется пересечение по Минковскому разбиений А¹,..., А^п ^ F ;

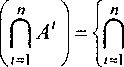
а’ :а‘ &A‘,i- 1,

Элементы Э-сетки - события-терраски вида

п

• -    называются Э-ячейками Э-сетки Sⁿ.

Ясно, что

О = У ••• У ter, 1     = У ter, , а еЛ а”еЛ”               ter ,   . eS”

• -    Э-ячейки образуют разбиение пространства элементарных событий Q.

Таким образом, Э-сетка имеет вид:

S" =|ter_{al а‘еА‘, z = 1, ...,д|.

Несмотря на кажущуюся простоту, вопрос о выборе Э-сетки заслуживает внимания. С одной стороны, количество событий-террасок желательно брать большим, т.е. пользоваться мелкими, подробными Э-сетками. Точнее передавая при этом область изменения Э-аргумента, мы интуитивно рассчитываем лучше аппроксимировать искомое Э-распределение сеточными распределениями. С другой стороны, практические соображения, и в первую очередь ограниченность быстродействия и объема памяти компьютеров, заставляет обращаться к Э-сеткам со сравнительно небольшим числом Э-террасок. Решением этой проблемы часто служат неравновероятные Э-сетки. Если имеется информация об Э-распределении, например, известно «расположение» в пространстве элементарных событий некоторых его особенностей, для «разрешения» которых необходима мелкая Э-сетка, то можно, не увеличивая общего числа террасок, сгустить сетку в «окрестности» этих особенностей, а в «гладкой» области распределения сетку сделать редкой.

Определение 2.3.. X - аппроксимирующим 8^п -сеточным отображением называется отображение ф: 8^п -> 2 ^х, которое на Э-ячейке

(=1

принимает значение

’Л"е ^: xnter{a'...a"} которое сокращенно обозначается

Определение 2.4. 8^п - аппроксимацией множества событий X называется множество событий

Математика

Г={^:*еЯ где каждое событие х^ф = У (xnter i „ )                               (1)

• -<—<        \ а ...а /

х«р\ ter । „ I называется Sn -аппроксимацией события х е X .

Событие-терраску будем обозначать ter^)^Qx^p Q^)⁰, ХсХ.                 (2)

хеХ ХеХс

Приведем примеры X -аппроксимирующего S² отображения с различной степенью ошибки:

0	0	X	х	X
	У	х, у	X	X
У	у. 2	x,y,z	X, Z	X
У	У 2	у, Z	Z *7	0
0	Z	Z	«и Z	0

а Р 7   5   8

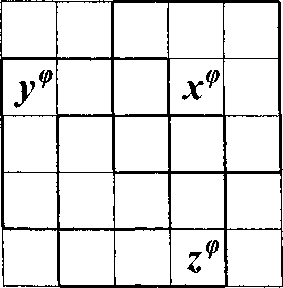
Рис. 1. Эвентологическая сетка второго порядка S² = {аДс,Де}(п){а, Д у,5,е^ , аппроксимирующая исходное Э-распределение триплета событий X = Ууу.г', с нулевой ошибкой (слева). Э-сеточная аппроксимация

Х^ф₌^_1ур_>2р^ _на э-ячейках (справа)

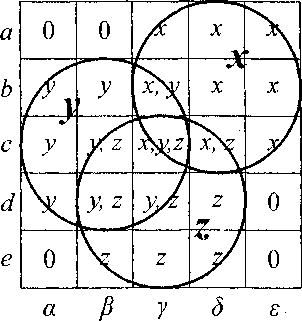
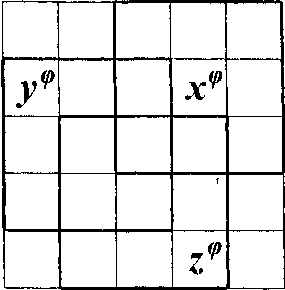
Рис. 2. Эвентологическая сетка второго порядка S² = {a, b, с, d, e)(n){a, Р, у, 8, г), аппроксимирующая исходное Э-распределение триплета событий X = ^x,y,z^ с некоторой ошибкой (слева). Э-сеточная аппроксимация X^s” = ^х^ф,у^ф,г^ф^ на Э-ячейках (справа)

Виды Э-сеточной аппроксимации

Точность Э-сеточной аппроксимации Э-распределений определяется структурой локальной зависимости аппроксимируемого множества событий, которая характеризуется отношением структур зависимостейдвух множеств событий, участвующих в Э-сеточной аппроксимации: Э-сетки S" и аппроксимируемого множества X .

Рассмотрим три вида Э-сеточной аппроксимации, каждый из которых справедлив в рамках одного из трех предположений о локальной структуре зависимости аппроксимируемого множества событий X : вложенной, независимой и наименее пересекающейся.

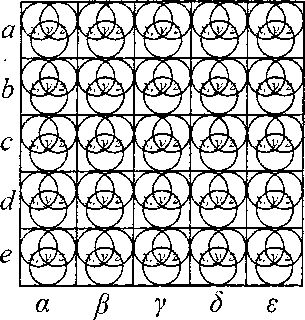
Рис. 3. Эвентологическая сетка второго порядка S² = {a, b, с, d, е}(п){а, 0, у, 5, е), аппроксимирующая исходное Э-распределение триплета событий X = ^x,y,z^ с наибольшей ошибкой (слева).

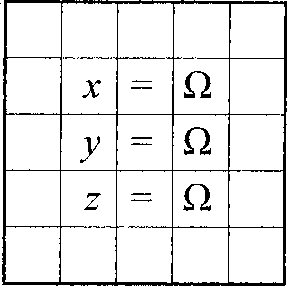
Э-сеточная аппроксимация Х^ = {П,П,П} на Э-ячейках (справа)

Определение 3.1. Множество событий X имеет локально вложенную структуру относи-п телъно Э-сетки Sn, если для любой Э-ячейки ter $ a„,=Qa'е 5’п и любого события та ter t „ =< т.е. либо ter t ^ содержится в х, либо не пересекается с ним.

Из этого определения следуют два свойства:

!) J ^Ater{a, aJ=ter{Z V},

• 2)    события х A ter । ^, где х е Х^,   , равновероятны.

Определение 3.2. Множество событий X имеет локально наименее пересекающуюся структуру относительно Э-сетки Sⁿ , если для любой Э-ячейки ter _{t о}„ eS" и любого множества событий X ₁ „ с X : а а

• 1)    I ^V.^J^V.V)’ _аП

события та ter, _f „,,где хеХ ] ^равновероятны, {а а }               а а

Определение 3.3. Множество событий X имеет локально независимую структуру относительно Э-сетки 8^п, если для любой Э-ячейки ter , _п е8^п и любого множества событий

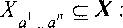
(J ^Ater^, ^J=ter{a. а„},

• 2)    события х n ter_{ai ^„^, где х g X_{qX а}„, равновероятны,

• 3)    события х п ter_{a, _q^, где х е Х^ _q„ , независимы в совокупности.

Теорема 3.1. Эвентологическое распределение Sⁿ -аппроксимации множества событий X р⁹ (^) = P(ter^ (X)), XqX