Методы теории рассеяния для решения задач дифракционной оптики

В последнее время большое внимание уделяется методам расчета дифракционных оптических элементов в рамках электромагнитной теории. Применение различных разностных схем к решению системы уравнений Максвелла требует значительных вычислительных ресурсов.

В данной работе предложен метод решения системы уравнений Максвелла для случая дифракции плоской электромагнитной волны на дифракционном оптическом элементе, представляющем собой тонкую пластинку с нанесенным на нее микрорельефом. Расчет проводится в рамках строгой электромагнитной теории. Метод основан на приведении исходной системы уравнений Максвелла к системе интегродифференциальных уравнений.

Рассмотрим прямую задачу дифракции.

Пусть освещающий пучок с заданными значениями векторов электрического и магнитного поля падает на дифракционный оптический элемент.

Анализируя оптическую схему, расположенную на рис. 1, можно выделить несколько областей: 1. между источником и дифракционным оптическим элементом,

• 2.    подложки,

• 3.    модуляции,

• 4.    между областью модуляции и регистратором.

Необходимо найти значение векторов электрического и магнитного поля в области регистратора.

Уравнения Максвелла для бивекторного поля

имеют вид:

i dW

--= HW , k d z

W =

E 1

E 2

E 3

E 4

где H - матричный дифференциальный оператор, называемый также оператором Гамильтона, E i , H i -

компоненты электрического и магнитного поля вдоль координатных осей x ⁱ.

В дальнейшем четырехкомпонентный вектор W будем называть бивектором, а соответствующее поле бивекторным электромагнитным полем. Выражение (1) можно рассматривать как операторную запись в абстрактном гильбертовом пространстве бивекторов. В этом случае система уравнений Максвелла приобретает стандартный вид эволюционно-

го уравнения.

В координатном представлении оператор

мильтона имеет следующий вид:

B

A

-1 a x , 0 k 2 [ 0 ^d x

£

- 1

£

- 1

a

a

⁵ x^{1 d} x i

- 1

Га-

в ^{1 Гд} B = k?

x ¹

d X x

^d X 2

d x

x

^d X

д X

x

£

£

-

где x‘ - декартовые координаты, e - диэлектрическая проницаемость среды.

Операторное уравнение (1) можно формально

1. Формальная теория рассеяния для бивекторного электромагнитного поля

В данном разделе изложен основы формального математического аппарата, который в дальнейшем будет использован для описания процессов дифракции света на дифракционных оптических элементах. Приводимый математический аппарат частично заимствован из квантовой механики [1] и теории взаимодействующих классических полей.

проинтегрировать:

W ( t ) = U ! ( t , t 0 ) W ( t o ) =

= exp ( - i ⁽ t - t o ) H ) ^{W (} t o ),

где

to

UI (t, t0) = 1 + X n=1

( - 1 ) n !

t           t n - 1

J d k n - 1 J d ^ n - 2

t n - 1            t n - 2

X

t ₂         t ₁

X J d ^ ! J d k 0 [ H ( k n - 1 ) H ( k n - 2 ). .. H ( k 1 ) H ( k 0 ) ] , t ₁         t ₀

где t=kz .

Здесь приведена запись уравнений в абстрактном операторном представлении. Для решения конкретных физических задач нужно все векторы и операторы записать в конкретном представлении.

Произвольную функцию из рассматриваемого линейного гильбертова пространства представим в виде линейной комбинации:

W = £ f n ( z ) F n ( x 1 , x 2 ) .                        (5)

n

Набор функций f ⁿ ( z ), будем называть волновой функцией бивекторного электромагнитного поля в f -представлении. Каждому абстрактному оператору в данном базисе можно сопоставить матрицу H_n^m

HFn = £ Hm (f)Fm (x 1, x 2).(6)

m

Система уравнений Максвелла в представлении записывается в виде: m j- ;=£ нт (z) fn (z).

k dz

В общем случае система базисных функций не является счетной. В этом случае суммирование заменяется интегрированием.

Базисные векторы в координатном представлении имеют вид:

⁸ m l

X y 1 y ₂ m ⁽ x 1 , x 2 ) = ^{8 (} x 1 - У 1 ⁾⁸⁽ x 2 - У 2 )

⁸ m 2

⁸ m 3

⁸ m 4

где 8 ( x ) - функция Дирака.

Бивекторное поле имеет вид:

W ( x 1 , x ² ) =

+^ m = 4    12

= f £ W”"X,_y 2 m ( x V x ² dy ¹ dy 2

-to m = 1

В дальнейшем для записи выражений будем использовать правило Эйнштейна, согласно которому по повторяющимся индексам производится суммирование или интегрирование.

Если в пространстве существуют два базиса, связанные соотношением

Vm = S"m (v ^ f)Fn , (9) тогда волновые функции бивекторных полей и матричные элементы операторов в различных представлениях связаны соотношением fn = sm (v ^ f) vm, (10)

H q ( f ) = s m ( f ^ v ) H m ( g ) s q ( v ^ f ) ,    (11)

где H ( g ) _l ^q , H ( f ) _l ^q - матричные элементы в G - и F -представлении.

Пусть бивекторное поле имеет следующий вид:

в области 1

W(x 1, x2, z)= qn (z) Qn (x 1, x2), в области модуляции

W (x 1, x 2, z )= fn (z) Fn (x 1, x 2),(13)

в области 4

W(x 1, x2, z)= vn (z) Vn (x 1, x2).(14)

Пусть связь между базисными векторами в F-, G- и Q -представлениях имеет вид

Vm =(x 1, x2 )= sm (v ^ f) Fn (x 1, x2),(15)

Fm =( x 1, x 2 )= Sm (f ^ q ) QFn (x 1, x 2 ).

На границе области модуляции и области 4 волновая функция бивекторного поля в G -представлении имеет вид v^m (0) . Запишем ее в F -представлении:

fn (0) = sm (v ^ f)vm (0).(17)

Поле в произвольной точке в области модуляции имеет вид:

fn (z) = U"m (z)fm (0),(18)

где эволюционная матрица удовлетворяет уравнению

7 ^Umm^^) = Hl (z) Um (z)(19)

kd с начальными условиями U*n (0) = 8 m .

Бивекторное поле в F -представлении на границе области модуляции и области 1 имеет вид:

fn (-a) = U"m (-a) fm (0).(20)

То же самое в Q -представлении:

qn (-a) = sm (f ^ q) fm (-a).(21)

Подставляя выражение в (20) и (21), получаем q n (-a) = sm (f ^ q) x Um (-a) slj (f ^ q)vj (0).(22)

Полученное выражение можно рассматривать как систему линейных алгебраических уравнений относительно коэффициентов qⁿ ( - a ) и v^k (0).

Выражение (22) можно переписать в эквивалентной форме sn (q ^ f) qn (-a) = UP (- a) sj (q ^ f) vj (0).   (23)

В данном случае интегрирование дифференциального уравнения для эволюционной матрицы проводилось в направлении противоположном направлению оси z . Рассмотрим метод, в котором интегрирование эволюционного уравнения проводится в направлении оси z .

Пусть qn (-a) - волновая функция бивекторно-го поля в Q-представлении на границе области модуляции и области 1. Запишем ее в F-представлении fn (-a) = smm (q ^ f)qm (-a). Поле в произвольной точке в области модуляции имеет вид fn (z) = Um (z) fm (-a),                     (24)

где эволюционная матрица удовлетворяет уравнению

L 9 U m ( z ) _ " I

, _a = H l ⁽ z ) U m ⁽ z )

k   оz с начальными условиями Umm (-a) = 6 m .

Бивекторное поле в F -представлении на границе области модуляции и области 1 имеет вид:

f" (0) = U"(z) Sm (q ^ f)qm (-a).(25)

То же самое в V-представлении v" (0) = sm (f ^ v)fm (0).(26)

Подставляя выражение (25) в (26), получаем v" (0) = sm (f ^ v)Um (0)Sk (q ^ f)qk (-a).(27)

Полученное выражение можно рассматривать как систему линейных алгебраических уравнений относительно коэффициентов q" ( - a ) и v^k (0).

Выражение (27) можно переписать в следующем виде

S n ( v ^ f ) v n (0) = U j (0) S { ( q ^ f ) q^k ( - a ).      (28)

Вышеизложенный метод применим для решения широкого класса задач дифракции, как в свободном пространстве, так и в среде (например, в волокне). Выбор представления зависит от конкретной задачи. В качестве базисных функций удобно использовать собственные функции оператора Гамильтона. В этом представлении система уравнений Максвелла имеют наиболее простой вид.

2. Ковариантная запись системы уравнений Максвелла в криволинейных координатах.

В предыдущем разделе исследовалась система уравнений Максвелла в декартовых координатах. В данном разделе получим систему уравнений Максвелла в параболической форме в ковариантном виде. Ковариантная запись позволяет легко записывать выражения в произвольной системе координат.

Для записи уравнения Максвелла в криволинейной системе координат введем тензоры

E n , Dⁿ , H n , Bⁿ ,

g 13 = g23 = 0,(32)

g 33 = 1,(33)

sid3Ej = -ik (Vg)giHj + 8idjE3,(34)

^s j a 3 H j = - ik ⁽V V ) g⁴E j + ^s4 8 j H 3 ,

2 s "m 3 (8 "Em-8 mE" ) = tiH3 Vg,(35)

2s"m3 (8"Hm -8mH" ) = ikE3 Vg .(36)

Выражаем E ³, H ³ из последних двух выражений, и, подставляя в первую пару уравнений, получаем:

s ^ij 8 3 E j =- ik (V g ) g i H j -

-

s ^ij 8 j

' s " ^{m 3} ( d " H m -8 m H " ) ' _v      2 ik/g        _?

^s i a 3 H j =- ik ⁽V F ) g i E j -

s ^j a j

s ""m ³ ( 8 " E m -8 m E " ) ' _v       2 k.Jg       _?

Рассмотрим случай ортогональных криволи-

нейных координат. В этом случае система уравне-

ний Максвелла относительно четырех компонентных бивекторов имеет вид:

i 8 W = HW ,                      (39)

k

где

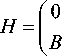
A

где

D " = s g-E m , B n = H ,             (29)

где

s - диэлектрическая проницаемость среды.

Система уравнений Максвелла в криволинейных координатах в ковариантной форме имеет вид

A = - 1 f^d у ¹ 0 Y^(s ) 1 k ² V 0 d y 2 Д 0

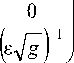
( rot H ) " = - ikD " ,                           (30)

( rotE ) " = - ikB " ,                           (31)

S^-d y 2

V^-d y 2

d y 1

8 y 1

-

V

g

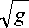
g

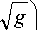
где оператор ( rot F ) "

представляется в виде

( rotF ) "

s i" [ d F j    a F i

2 V g V d x i    8x^j

X |^d y 1    ⁰

k ² V 0 d y 2

g = det ⁽ g ij ) ,

X

-

( )

g _ij - компоненты метрического тензора в криволинейной системе координат.

Рассмотрим криволинейную систему координат, в которой метрический тензор имеет вид

d y 2

d y 2

d y 1

d y 1

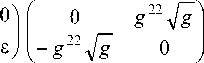
Отметим, что при переходе от одной системы

криволинейных координат к другой компоненты четырехкомпонентного бивектора - верхняя и нижняя

половины бивектора - преобразуются как двумерные векторы.

3. Пространственно-частотное представление системы уравнений Максвелла

Многие задачи дифракционной оптики значи- тельно упрощаются при переходе к пространственно-частотному представлению.

Базисные функции    F-пространственно частотного представления имеют вид:

		"5 1 i	exp	ik	a	x 1	2 + a 2 x ))
Fnn , ( x 1 a. an , z \ 12	, x 2 ) =	5 2 i	exp	( ik	a	1 x 1 1	+ a 2 x 2 )) 2	,      (44)
		5 3 i	exp	. ik	a	x 1	+ a 2 x ))
		.5 4i	exp	( ik	a	1 x 1	2 + a 2 x ))

A	12 — — © 1 © 2	" i a 1 . 0	0 i a2		e 1 (a. 1 -© 1 , a 2 -© 2 ) x
x	- i “ 2	i © 1 "	-	Г 0	1 "	5a 5a ,
	.- i © 2	i © 1 _		L- 1	0 _	© 1    © 1 ,

B a 1O(.2 = - “ 1 © 2	■ i a 1      0 " . 0 ia 2 _	■ - ”2 - i © 2		i © 1 " i © 1 _		5a 1 5a 1 - © 1 © 1
-1/			■ 0	1 "
- e ( a 1 -	© 1 , a 2 -to	2 )	.- 1	0 _	,

5 © = 5 ( a - to ) - дельта-функция Дирака.

Уравнения Максвелла в пространственночастотном представлении приобретают вид:

где 5 ik - символ Кронекера.

Связь между базисными функциями координатного и F -пространственно-частотного представления имеет вид

/ .   _ \ к = 4 +”   12,,

F _aa Д x Д x ² ) = X f S ^yyk ( f ^ x ) x

¹ 2^Л          Г 1 , ^{a 21}                 (45)

^{X X} _y ' у 2 , k ^{( x} ^ ^{x 2 )} dy ¹ dy ² .

Связь между волновыми функциями координатного и F -пространственно-частотного представления имеет вид

_{W y} 1 _y 2 _k

к = 4 ⁺ ”     1 2, ,

= X f S^yyk ( f ^ x ) x

J a^a?, iv        / к=1 -*

i df a1“2 k   dz - = H a © oc 2 i T*©1©2 ©2 k J k . (51) Для вакуума уравнения приобретают вид: i df a1“2 k   dz = H a a 1 2i f a2k J a1a k . (52) H a1<^2 _ 12 . 0 B a1CC2 12 A a1a2 a1 a 2 0 _ ’ A аха2 = 12 " i a1 . 0 0" i a 2 Г-ia 2 - i a 2 ia1 " i a1 _ - Г0 -1 1" 0_ , B a1OC2 = 12 i a1 0 0" i a 2 ■- - " a 2 " a 2 ia1 " i a1 _ - Г0 L-1 1" °J . где

X y ¹ y 2 , m ^{( x} ’ x ⁾ =

= 5 ( x ¹ - y ¹ ) 5 ( x ² - y ² )

5,

m 1

m 2

.

m 3

m 4

Отметим, что в формуле (52) нет суммирования или интегрирования по повторяющимся индексам и система уравнений распадается на множество систем из четырех обыкновенных дифференциальных уравнений. Уравнения (52) имеют чтыре линейно независимых решения следующего вида:

Матрица преобразования имеет вид

S a Oa’ki ( f ^ x ) = exp ( ik ( a ₁ x ¹ +a ₂ x ² )) s ^k .        (48)

Матрица обратного преобразования имеет вид

	■ f « 1 « 2 , 1 "  f ± e г « 1 « 2 ,2 f ± e. , f « 1 « 2 - 3 f ± e Л r « 1 « 2 - 4 J ± e		■ ('	1 1 - a 2 -	a 2 2	j a 1
f a 1 a 2 = f ± e =		=1 W\ Г1	T	1 1 - a 2 -	a 2 2	J a 2	x
				a2				(53)
			L	- a 1		J

s x aj _k '( x ^ f ) =

^k      12 i

= 4— exp ( - ik ( a i x +a 2 x )) 5 к .

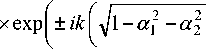
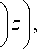
Гамильтониан в пространственно-частотном представлении имеет вид

H ^a 1^a2

1 © 2

A ^a 1^a2 © 1 © 2

		■ f a 1 « 2 > 1 "  f ± e. г « 1 « 2 ,2 f ± e. , r a 1 a 2 ,3 j ± e		Г	- a -2 a 1	1
r a 1 a 2 f ± h	=		=1 W l Г1	■ ('	/1 - a 2 - a 2 2	1 a 1	x	(54)
		. f^2,4 _		. ■	/1 - a 2 - a 2 2	] a 2 J
x exp	±	ik [ д/1 - a 2 - a 2 1		z 1 ,

IIW1I = J («2 + « 2) f' + 11 -a2 « 2 |

Введем V-пространственно-частотное представление (V-представление). В качестве базисных функций V-представления выберем собственные функции оператора Гамильтона для бивекторного поля, распространяющегося в вакууме. Базисные функции V-пространственно-частотного представления связаны с базисными функциями F- представления

V ““ n ^{( x} 1 , x 2 ) =

= ^s “« П ⁽ V ^ f ) F a , a ₂ n ⁽ X ' > X ^

s ““2n (v ^ f M«2 5“ sm (v ^ f),(56)

		г “|“ n f + e	m	= 1
s mm ( V ^ f ) =		“ “ n f + h f-Tn	m m	= 2 = 3
		r “,“ n f - h	m	= 4

W = W0 (x', x2 )= Wx'x 2 k (0).(6')

Для вычисления поля в произвольной плоскости перейдем от координатного представления к пространственно-частотному представлению f «'«2, i (0) = s;«x“2 k i (x ^ f) wx'x 2 k (0).(62)

V«'a2’/ (0) = s““n (f ^ V) f “'“2n (0).(63)

Матричные элементы гамильтониана в вакууме в V -представлении H “^k есть элементы следующей матрицы:

H « '“2 ( v ) = - ik 5 « ' 5 « ' x

“ ' “ 2                 “ ' “ '

	Г ' 0 0 0 1
/-.         2         2	0'00	(64)
x Л ' — « ' — «2
	0 0 — ' 0
	_ 0 0 0    — ' _

Решая систему уравнений Максвелла в V -представлении для произвольной плоскости, получим

Тензор обратного преобразования выглядит следующим образом

S “ ' “ 2 p ( f ^ v ) = 5 “ ' 5 “ ' ( m ' ) p P n ,         (57)

« ' « 2 m V ⁷    « 2 a' \      /n m ,            ^{v 7}

		V « '“21 (0)exp I	ik Ф	— « 2	1 — « 2 z I
V « ' « 2 1 ( z )			f		<
2 V ' 2 ( z )	=	v «'“ 2 2 (0)exp	Jk,]	— « 2	— « 2 z J	.(65)
V «'“ 2 3 ( z )		v «'“2 3 (0) exp f	— ik^	' — « 2	— « 2 z ]
4 V ' 2 ( z )		f			)
		«1«Э 4 /А\      I V ' 2 (0)exp I	— ik^	' — « 2	2 —« 2 z J

Далее перейдем от V -представления к координатному представлению

где матрица P_mⁿ есть матрица эрмитовосопряженная по отношению к матрице S mm ( v ^ f ) , а матрица M mm = P k S m ( v ^ f ) . Здесь верхний индекс означает номер строки в матрице, а нижний индекс - номер столбца.

	Г	1	0	W ±	0 1
M =	0      ' W ± 0			0 1	W ± 0	,			(58)
	L	0	W ±	0	' _
		Г	1	0	— W ±	0 "
M "'	—	—	0 W ±	1 0	0 1	— W ± 0	x '	1 — W ±l2 .	(59)
		L	0     —	W ±	0	' J

f « '«2 n ( z ) = s « '“ ^{2 n} ( V ^ f ) V “ ' “^{2 n} ( z ),

^{J V 7}      “'“2 n         ^J '          v / ,

W^x ' ^{x 2} , ^k ( z ) = S « ^x ' ^x 2 ’ k ( f ^ X ) f « '“ ² i ( z ).        (67)

Выражение описывает бивекторное электромагнитное поле в плоскости регистратора.

Волновые функции бивекторных полей в этих двух различных представлениях связаны следующим образом

f

a ₁ a ₂ n

= s « ' « ^{2 n} ( v ^ f ) v “ ' “ ^{2 n}_

° “'“2 n V ⁷ /         ,

V « ' « 2 n

1 « ' « 2 n “ ' “ 2 n

(f ^ V ) f

^“ ' ^“ 2 ⁿ

4. Распространение бивекторного электромагнитного поля в вакууме

В настоящем разделе рассмотрим задачу распространения бивекторного электромагнитного поля в свободном пространстве.

Пусть в плоскости z =0 бивекторное поле имеет вид:

5. Дифракция на пропускающих дифракционных оптических элементах

Рассмотрим дифракцию света на пропускающих дифракционных оптических элементах

Пусть v «'“2n (-a) - волновая функция бивек-торного поля в V-пространственно-частотном представлении на границе области модуляции и области 1. Запишем ее в F-пространственно-частотном представлении f «'“2n (-a) = sm (v ^ f) v “'“2m (-a).         (68)

Поле в произвольной точке в области модуляции имеет вид:

f “ ' “ 2 n ( z ) = и ““ 2 m ( z ) f « '«2 ^m ( — a ),           (69)

где эволюционная матрица U_mⁿ ( z ) удовлетворяет интегро-дифференциальному уравнению

d U “ ' “ 2 n

----““ m = H “'“ 2 n ( z ) и ^{3 1 3 2} l ( z )

k 5z           P 1 P 2 l ^V ' “ ' “ 2 m^v '

с начальными условиями

U ““ 2 n ( - a ) 5 “ 2 5 “ ' 5 n . “ ' “ 2 m a 2 “ ' m

Полученное выражение представляет интегро-дифференциальное уравнение.

(71) собой

Бивекторное поле в F-представлении на границе области модуляции и области 4 имеет вид:

f “ ' “ 2 n (0) =

= U “ ' “ 2 n (0) S. “ ' “ ² j ( v ^ f ) v ^{в 1 в} 2 ^m ( - a ).

“ ' “ 2 j ^{v 7} P 1 P 2 m ^{v 77         v 7}

То же самое в V-представлении v a'a2 n (0)=s “y f ^ v) f 3132 m (0).

пространственно-частотном представлениях имеет следующий вид:

f nm’i (0) = S™pk (x ^ f)Wx'x2,k (0),(79)

Snm,‘(x ^ f ) = —-—exp (k (amx' + a™x2 ))^i,(80)

x1x2,k               d1d2             12 d1 d2 - размеры дифракционного оптического элемента или периоды периодической двумерной структуры.

Тензор обратного преобразования имеет вид:

Si ^’ k ( f ^ x ) = exP ( ik ( “ im x ' +“ m x 2 )) 5 k . (8')

Гамильтониан в дискретном пространственночастотном представлении имеет вид

Подставляя выражение (72) в (73), получаем:

v «, , . (0) = S -„ ( f ^ v ) и “ ' “ 2 m _{(0) x}         74

* S ““ j v ^ f ) v "2 ‘ ( - a )•

np mq

np mq

-

np mq

np mq

Полученное выражение (74) представляет собой связь между полями v “ ' “ 2 n ( - a ) и v “ ' “ 2 ^k (0) на границах области модуляции. Выражение (74) можно переписать в следующем виде:

-

i “ П

i “ 2p

- '

n - m , p - q

- i “ m - i “ m

i “ q i “ q

5 m

^p q ^,

S ““ P ( v ^ f ) v “'“ ² n......

= U ““ j '(0) S ”2 k ( v ^ f ) v ”2 ^k ( - a ).

np mq

-

i “ П

0     - i “ 2

i “ P J [- i “ m

i “ qq i “ ^q

5 m 5 p

-

На практике поле удовлетворяет следующим условиям.

Условие 1 . Поле прошедшее через оптический элемент не содержит волн, распространяющихся против оси z :

v ^{nn 2} 3 (0) = v ^{nn 2} 4 (0) = 0.                     (76)

Условие 2. Компоненты определяются из условия задачи. Они описывают бивекторное поле в отсутствии ДОЭ. На практике при решении задач дифракции падающее и прошедшее поле удобно задавать в координатном представлении. В этом случае необходимо в выражении для падающего поля перейти от координатного представления к V-представлению, используя формулы f ““2,i(-a) = S“'“22,i(x ^ f) wx'x2,k (-a), (77) xx ,k

-

- '

n - m , p - q •

Формулы (75) в дискретном пространственночастотном представлении имеют вид:

s mjq ( v ^ f ) v mq (0) =

= U j (0) ST ( v ^ f ) v slr ( - a ).

Отметим, что в отличие от обычного пространственно-частотного представления, в дискретном случае интегральное уравнение превращается в систему линейных алгебраических уравнений. Матрицы перехода от F -представления к V -представлению и обратно имеют вид:

S kPm ( v ^ f ) = 5 k 5 p s m ( v ^ f ) ,           (84)

S Tqm ( f ^ v ) =5 j 5 q ( m ^- ' ) k P mk .             (85)

v “ ' “ 2 n ( - a ) = S ““ n ( f ^ v ) f “ '^m2 n ( - a ).      (78)

Решая систему интегральных уравнений (75) и используя результаты, полученные в предыдущем пункте, определяем прошедшее бивекторное поле в области 4.

Интегро-дифференциальное уравнение для эволюционной матрицы в дискретном пространственночастотном представлении превращается в систему обыкновенных дифференциальных уравнений i a unlk( z)

L^jT! = H sr ( z ) U j ( z )          (86)

k    dz с начальными условиями

U mp ( - a ) = 5 m 5 ij 5 p .

Формулы (84), (85), (86) могут быть получены из формул (56), (57), (70)< если заменить интегралы на интегральные суммы.

• 7.    Реализация вычислений

Для того чтобы получить систему линейных алгебраических уравнений (83), необходимо многократное уравнение для эволюционной матрицы (86). Решение эволюционного уравнения сводится к решению системы обыкновенных дифференциальных уравнений с различными начальными условиями. Это позволяет использовать технику параллельных вычислений. В данном случае был использован под- ход, состоящий в том, чтобы система уравнений для различных начальных условий решалась на различных компьютерах. Приводимые ниже результаты были получены с использованием кластера, состоящего из четырех двухпроцессорных компьютеров PENTIUN-II с частотой 450 МГц. Для решения системы обыкновенных дифференциальных уравнений использовались методы матричной экспоненты и Рунге-Кутта.

Рис. 2. Результаты расчета проекции вектора Умова-Пойтинга на оптическую ось для дифракции плоской электромагнитной волны на радиально-симметричной бинарной линзе в плоскости z=0 (а, б), в плоскости z=f/2 (в, г), в плоскости z=f (д, е), z=3f/2 (ж, з).

Рис. 3. Результаты расчета проекции вектора Умова-Пойтинга на оптическую ось для дифракции плоской электромагнитной волны на радиально-симметричной бинарной линзе в плоскости zx.

В качестве примера был выбран расчет поля от бинарной цилиндрической линзы.

При расчете были использованы следующие параметры: радиус апертуры R=4,82λ, фокусное расстояние f=4,82λ. На рисунках 2, 3 приведены результаты расчета проекции вектора Умова– Пойтинга на оптическую ось для дифракции плоской электромагнитной волны на бинарной радиально-симметричной линзе на различных расстояниях от оптического элемента. При этом на рисунках черный цвет соответствует максимальному значению. Приведенные выше результаты показывают работоспособность приведенного алгоритма. Разработанный метод снижает требования к вычислительным ресурсам, по сравнению с многомерными разностными методами. Анализ полученных результатов показывает, что максимум интенсивности в фокусе линзы примерно в четыре раза меньше значения, рассчитанного в скалярном приближении Кирхгофа. Однако, несмотря на это, бинарная линза сохраняет свои фокусирующие свойства. Следует отметить, что в отличие от скалярной теории, фокальное пятно имеет слегка вытянутую форму. Это объясняется тем, что в рамках электромагнитной теории не существует радиально-симметричных ре- шений даже в случае дифракции плоской волны на радиально-симметричном объекте. Радиальная симметрия нарушается за счет наличия поляризации у падающей электромагнитной волны.

Заключение

В работе предложен компактный математический аппарат для решения задач дифракции плоской электромагнитной волны на дифракционном оптическом элементе. Математический аппарат позволяет однообразно описать различные задачи дифракционной оптики и свести многие задачи к решению системы обыкновенных дифференциальных уравнений с различными начальными условиями. Это позволяет в свою очередь использовать технику параллельных вычислений. Предложенные в работе методы апробированы на решении задачи дифракции плоской электромагнитной волны на бинарной линзе Френеля.