Методы восстановления изображений и распознавание образов в радиоастрономии

В радиоастрономии радиотелескоп играет роль линейного оператора, воздействующего на функцию, описывающую объект исследования. Формирование изображения наблюдаемого объекта может быть представлено в этом случае интегральным уравнением Фредгольма I-го рода [Есепкина и др. 1973; Гончарский и др. 1973]:

+ R + R

J J h ( x - X i , y - y i ) f ( X i , y i ) dx i dy =

• - R - R

• = g ( x , y ) + n ( x , y ) ,                                      (1)

где g ( x , y ) есть наблюдаемое распределение радиояркости; f ( x 1 , y 1 ) – истинное распределение радиояркости; h ( x , y ) – передаточная функция инструмента (или диаграмма направленности (ДН) телескопа); n ( x , y ) – стационарный аддитивный гауссов шум.

Задача решения данного уравнения является некорректно поставленной по Адамару, поскольку спектр пространственных частот наблюдаемого изображения g ( x , y ) ограничен передаточной функцией инструмента. На практике задача осложняется еще и тем, что функция ядра h ( x , y ) в уравнении (1) может сильно отличаться от расчетной, становясь несимметричной и с боковыми лепестками, значительно превышающими по амплитуде расчетные. В этом случае в изображении g ( x , y ), кроме боковых лепестков, присутствует перекос уровня спокойного Солнца. Все это, а также наличие шумов в изображении приводит нас к необходимости как создания новых, так и развития уже существующих методов приближенного восстановления радиоизображений наблюдаемых объектов.

Все существующие методы восстановления для уравнения (1) можно условно разделить на две группы:

• 1)    методы, восстанавливающие изображение в пределах полосы пропускания;

• 2)    методы, производящие экстраполяцию спектра за область спектральной чувствительности.

2. Поиск приближенного решения уравнения (1) с h 1 ( x , y ):

В радиоастрономии наибольшее распространение получили методы регуляризации по Тихонову [Тихонов и др. 1983; Василенко, Тараторин, 1986], метод максимальной энтропии (ММЭ) [Friden, 1972; Ables, 1974], итерационный алгоритм CLEAN [Hög-bom, 1974] и его модификации (см. работу [Cornwell, 2009] и ссылки в ней), относящиеся к первой группе, а также методы, использующие априорную информацию и относящиеся ко второй группе, такие как метод проекций на замкнутые выпуклые множества (ПЗВМ) [Брэгман, 1965; Губин и др., 1967; Юла, 1992; Сезан, Старк, 1992] и др.

В настоящей работе мы даем краткий обзор методов восстановления и коррекции радиоизображений Солнца алгоритмами проекций на замкнутые выпуклые множества (ПЗВМ), модифицированным фильтром Винера–Тихонова, методом CLEAN. На примере материала, полученного на Сибирском солнечном радиотелескопе (ССРТ) [Смольков и др., 2004], и других экспериментальных данных продемонстрированы возможности этих методов, показаны их преимущества и недостатки.

Метод регуляризации Винера–Тихонова. Алгоритм восстановления в пределах полосы пропускания ССРТ

Поскольку спектральная характеристика диаграммы направленности ССРТ является равномерно заполненной [Лесовой и др., 1998], то проблемы, возникающие на большинстве подобных инструментов (радиогелиографе Нобеяма, VLA) и связанные с нулями внутри спектральной области пропускания инструмента, отсутствуют.

На первый план выдвигается задача определения точной диаграммы направленности, поэтому в качестве одного из методов восстановления был выбран метод, основанный на модификации фильтра Винера–Тихонова [Василенко, Тараторин, 1986; Кузнецова и др., 2007]. Основная идея метода состоит в нахождении оптимальной частотной характеристики фильтра на основе подбора параметров σ, µ, α:

F m , n ^{( о} , ц, ^Z , ^{a )} =

H^k m , n

σ

■ X

Y ( u , V , g , ц, a) =

H ( u , V )

| H ( u , V )| 2

| H ( u , v)|² + a Q ( u , V )

H m ^k , n ²

I Hmm, n|2 + a(1 + m 2 + n2)

^G m , n

1 + Z( m ² + n ²)

здесь H ( u , ν) – передаточная функция телескопа в фурье-представлении, Q ( u , ν) – стабилизирующий функционал.

Поскольку огибающая функция спектральной характеристики H ( u , ν) имеет П-образную характе-

ристику с резкими краями, в восстановленном изображении неизбежно будут присутствовать дефекты, связанные с эффектом Гиббса. Для подавления этого эффекта и с учетом того, что высокие гармоники в функции H ( u , ν) определяются с меньшей

степенью точности, на предварительном этапе применения фильтра (2) используется фильтр низкой частоты Хэмминга. Дополнительно в частотную характеристику фильтра (2) была внесена добавка 1/[1+λ( u ²+ν²)], позволяющая обеспечить плавные края

спектра и сгладить остатки аддитивного высокочастотного шума в восстановленном изображении:

Y ( u , V , g , ц, Z, a) =

H ( u , V )

| H ( u , V )| 2

| H ( u , V )|2 + a Q ( u , V )

1 + Z( u ² +V ²),

где 0- параметр низкочастотного фильтра.

Практически наилучшее качество восстановления радиоизображения достигается при µ=0.5, σ =0.9–1. Параметр регуляризации α меняется в пределах от 10–5 до 10–7 и подбирается индивидуально в процессе восстановления изображения. Из формы эволюционного фильтра видно:

• 1)    при σ = 1, µ = 0 фильтр становится чисто инверсным;

• 2)    при σ =1, µ = 1 – регуляризирующим (в частном случае – винеровским);

• 3)    при σ = 1, µ = 0.5 – гомоморфным (среднегеометрическим).

Таким образом, алгоритм восстановления в полосе принимаемых пространственных частот можно представить следующим образом:

1. Определение приближенной h ₁( x , y ) как результат решения уравнения (1) относительно неизвестной аппаратной функции:

_F * _G

H1     _ m, n^m, n m, n, α               2                               ,

| Fm, n| + a(1 + m + n )

где m , n =1, …, N – дискреты изображения, F_{m, n} есть фурье-преобразование гауссиана, аппроксимирующего выбранный источник, G m, _n - «грязная» карта.

• 3.    Обратное фурье-преобразование F m, n → f m, n .

• 4.    Коррекция H_m ^k _{, n} исходя из соображений минимизации

• 5.    Переход к шагу (2), и так до тех пор, пока не выполнится условие R * , R * <  е. mn

R * =1 Fk* -sell и R * =1 Fk * -SqI’ m       m , n Q       n       m, n Q где Sq - уровень спокойного Солнца, значения n*, m* соответствуют координатам выбранного источника.

При линейном процессе восстановления пространственно-ограниченного объекта все частоты определяются в пределах полосы пропускания через процедуру деконволюции в совокупности с низкочастотным фильтром, что, в свою очередь, ведет к ухудшению разрешения. Поэтому при восстановлении объектов на Солнце, для исследования которых важно высокое разрешение, используются нелинейные алгоритмы, позволяющие подавить явление Гиббса тем, что привносят дополнительные высокие частоты, таким образом приводя к расширению полосы пропускания, или так называемому «сверхразрешению».

Заметим, что изложенный метод оправдан для случая не слишком больших искажений и зашумленности радиоизображений.

Метод чистки (CLEAN)

Одной из наиболее успешных процедур восстановления является алгоритм чистки (CLEAN), разработанный Хёгбомом [Högbom, 1974] (см. также [Cornwell, 2009]) для точечных источников. Он представляет собой процесс численного обращения свертки в области сигнала.

В 80-е гг. появилось несколько модификаций базового алгоритма Хёгбома. Для изображений больших размеров, требующих многих тысяч итераций по методу чистки, более быстрый вариант этого алгоритма разработан Кларком [Clark, 1980]. Затем Корнвеллом [Cornwell, 1983] предложены два варианта для стабилизации и уменьшения искажающих эффектов: SSC – чистка, стабилизированная сглаживанием, ESC – чистка, стабилизированная энтропией. При малом значении усиления X алгоритм SSC эффективен для понижения искажений ценой асимптотического поведения процесса. Кроме того, стоит отметить, что вторая методика (ESC) не может быть практически использована, так как процесс не всегда сходится.

Позднее в работах Стира [Steer et al., 1984] и Агафонова [Агафонов, 2003] представлена существенная модификация алгоритма чистки, в которой

для выбора компонентов в каждой итерации используется метод приспособленного контура. Ценные качества алгоритма особенно заметны при обработке протяженных областей.

Кратко остановимся на классическом методе Хёгбома. Рассмотрим уравнение (1) в одномерном варианте:

g ( x ) = J h ( x - X 1 ) f ( X 1 ) dX i .

Допустим, что

M f ( x) = T P ( K )5( x - Xk ), k=1

где P ( k ) – функция, составленная из коэффициентов, тогда

NN

g(x)=Thh(x - xii) f(xu) =T h(x - xi--)x i=1

M xT P(K)5( xii- xk)= k =1

m

=TP(K)Th(x -x)51xii--xk)= k=1

M

= T P ( K ) h ( x - x k ).

k = 1

Отсюда видно, что функция g ( x ) представима в виде суммы бесконечного числа функций – диаграмм направленности. Функцию g ( x ) называют «грязной» картой, а функцию h ( x ) – «грязным» лучом. Из этих соображений следует чисто эмпирический алгоритм, связанный с вычитанием «грязного» луча из «грязной» карты, разбиением распределения яркости на отклики от точечных источников, а затем с заменой каждого из них на отклик «чистого» луча, т. е. на диаграмму без боковых лепестков. Основные этапы заключаются в следующем:

• 1.    Находится наиболее яркий элемент изображения a l, m в искаженном изображении, т. е. такой элемент, что a j , k >  a l , m при всех l ≠ j и m ≠ k .

• 2.    Новое очищенное изображение находится путем операции сложения:

• 3.    Новое искаженное изображение находится с помощью операции вычитания:

^fcl , m ^{+ T} a j , k ⁵ 1 - j , m - k ^{— f}c l , m ■

• a, — T a • > h        —— a, ,

• l ,    m j , k             l - j , m - k l , m ,

• 4.    Процедура возвращается к этапу 1, если не выполняется условие a_l m <  c при всех l и m .

• 5.    Очищенное изображение свертывается с идеальным лучом h ( x ), имеющим основной лепесток и сильно уменьшенные боковые.

Й h ( l , m )

где τ<1.

Главное достоинство метода – это его простота. Отрицательные качества алгоритма – это малая скорость вычислений и вероятные искажения в виде морщин и «овражной» структуры, которая проявляется в протяженных областях. Стоит отметить, что алгоритм не содержит ясного критерия выбора параметров усиления.

Отметим также, что метод не предусматривает экстраполяцию спектра за пределы полосы пропускания.

Начиная с 2000 г. коллективом обсерватории ведется регулярное выставление в сеть Интернет солнечных карт ССРТ, восстановленных методом CLEAN (SSRT) [Lesovoy, 2002]. На рис. 1 представлены результаты обработки радиоизображений Cолнца, полученных на ССРТ и восстановленных с помощью эволюционного фильтра Винера–Тихонова и метода CLEAN, в сравнении с данными космического аппарата SOHO/EIT (Fe XII 195 Å).

Метод ПЗВМ для решения задачи восстановления радиоизображений

Впервые метод проекций на замкнутые выпуклые множества (ПЗВМ) был рассмотрен математиками Брэгманом [Брэгман, 1965] и Губиным [Губин и др., 1967], а затем развит в работах Юлы [Юла, 1992], Старка [Сезан, Старк, 1992], Бейтса [Бейтс и др., 1983], Барри, Медоффа [Барри, Медоффа, 1992], Хенсона [Хенсон, 1992] применительно к методу компьютерной томографии.

Пусть нам необходимо найти неизвестную функ-M цию f как лежащую на пересечении E0 = Q Ei хоро-i=1

шо обусловленных замкнутых выпуклых множеств E j cH , i =1, „., m , где H - гильбертово пространство. Пусть T : E — E : T = P_mP_m 1 ... P 1 , где P i - набор проекционных операторов на соответствующие множества E i , i = 1, …, m . Ясно, что f – неподвижная точка оператора P ₀ и всякого оператора T i = 1+ Х i ( P j -1) при произвольном выборе констант релаксации Х 1 , 1 2 , ..., X m .

Пусть E ₀ не пусто, тогда для всякого x е H и любого выбора констант λ 1 , λ 2 , …, λ m в интервале 0 < λ i <2 последовательность { t ” x } сходится слабо к точке множества E 0 .

Вернемся теперь к постановке нашей задачи. Нам необходимо восстановить f ( x , y ) – функцию радиояркости Солнца, f ( x , у ) е L 2 ( Q ), где L 2 ( Q )- квадратично интегрируемая функция на области Qc R ². Функция f ( x , y ) обладает следующими свойствами:

• 1.    Известно, что значения восстанавливаемой функции за пределами радиорадиуса Солнца должны быть нулевыми, поэтому искомая функция должна принадлежать множеству E 1 :

• 2.    Функция должна принимать предписанные значения G(u , v ) в замкнутой области Z c Q. Область зависит от заполнения фурье-плоскости ( u , ν) ДН. Данное множество функций E ₂ также является ЗЛМ.

• 3.    f ( x , у ) >  0 при x , у eQ . Это ограничение на неотрицательность решения вытекает из соображения

  

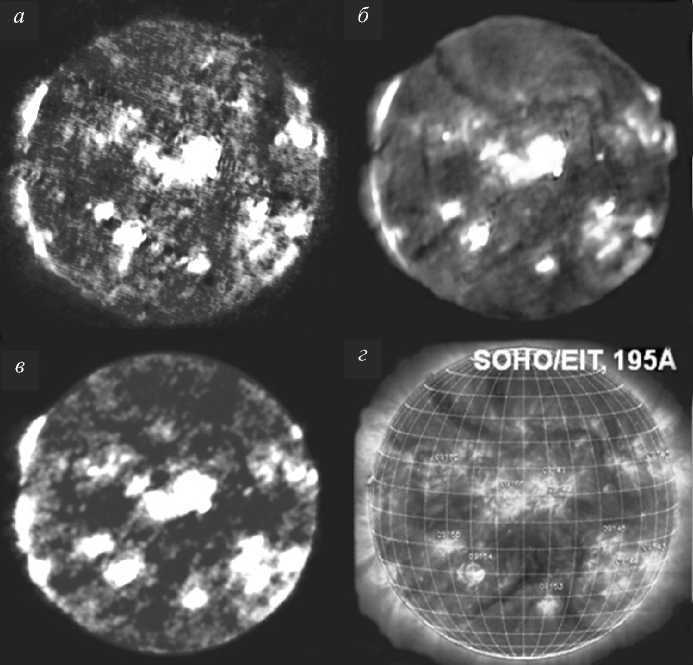
  Рис . 1. Изображения Солнца 4 сентября 2000 г .: а – « грязная » радиокарта на длине волны 5.2 см ; б – эта же карта по сле восстановления фильтром Винера – Тихонова ; в – она же после восстановления методом CLEAN (SSRT) [Lesovoy, 2002]; г – изображение Солнца в линии Fe XII 195 Å по данным КА SOHO/EIT.

  
  

  о положительности интенсивности. В [Youla, 1982] показано, что данное множество функций E 3 представляет собой выпуклый конус.

• 4.    jj| f ( x , У )| 2 dxdy <  E = P 2 , Ω

• 5.    Множество функций

• 6.    Пусть

[ 0, р ^{( x} , у ) >  R 0 , f ( x , у ) = <

[g(x, у), Р(x, у) ^ R0, где R0 – радиорадиус Солнца.

Множество таких функций является замкнутым линейным многообразием (ЗЛМ) без внутренних точек.

где ρ² – квадрат общего потока интенсивности, f ( x , y ) ∈ E ₃ . Данное ограничение справедливо только в том случае, когда на Солнце нет быстро протекающих процессов. За величину E принимаем значение потока невосстановленного радиоизображения. Множество таких функций выпукло и замкнуто.

f(x, y)≥Q–Q∙10 %, где Q – приближенная постоянная величина спокойного Солнца.

Это ограничение основано на том, что при наблюдениях на ССРТ интенсивности солнечного излучения в радиодиапазоне 5.2 см отсутствует депрессия больше 10 % от уровня спокойного Солнца. Множество E ₅ замкнуто и ограничено.

[ G ( u , v ) + n ( u , v) при ( u , v ) e Z ,

G ( u , v ) = <

• [ 0 при ( u , v ) 6 Z ,

где n ( u , ν) – шум в точке ( u , ν).

Введем характеристическую функцию X в виде fl при (u, v) e Z,

X = )

• [ 0 при ( u , v ) 6 Z .

Тогда G ( u , v ) = x G ( u , v ), и если F(u, v) - спектр неза-шумленного изображения fx , y ), то G ( u , v ) = x F ( u , v ) .

Будем рассматривать множество всех функций E ₆, фурье-образы которых S ( u , ν) удовлетворяют соотношению

||xS ( u , v) - ( G ( x , y )||

Это множество выпуклое и замкнутое.

Сформируем проекционные операторы к каждому из этих множеств. Обозначим через P i , i =1, …, 6, проекционные операторы на шести замкнутых выпуклых множествах, определенные в пунктах 1–6. Пусть f – произвольный элемент пространства H . Эти шесть операторов построены по следующим правилам.

• f ^f , P ^{( x} , У ) <  R 0 ,

• 1.    P f =               – оператор проецирования

• 2.    Pf ^ s               - дуальный к преды-

• 2      [F(u, v),(u, v) 6 Z

• 3.    Pf =                      - оператор про-

• [0, fi < 0,
4. P ₄ f = ^ f ⁺ , P . <  P ,

[0, p(x, y) > Rо на множество E1, R0– радиорадиус Солнца.

f G ( u , v ), ( u , v ) e Z ,

дущему оператор, учитывающий ограничения на спектральную протяженность. Область Z соответствует области определения ДН на плоскости ( u , ν). P 2 является проектором на множество E 2 по определению проецирующего оператора.

. I f , f 1 ^ 0, f = f 1 + jf 2 ,

ецирует известную функцию на множество положительных функций, приравнивая нулю все отрицательные участки.

0, f 1 <  0,

– проецирующий опе-

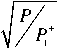
f+, P+ > P, ратор на область E4.

5. P 5 f =

Q , f ( x , y ) <  Q - Q - 10%,

.f ( x , y ), f ( x , y ) >  Q - Q - 10%,

– проектор

на множество E ₅.

F „ % F - G <0 ,

6. P₆ f ^ ^

%F,-G

G + XFT^ + (1 -X)F., %F — G >0, X Fi - G где X =

1,( u , v ) e Z ,

0,(u, v) ^ Z, x IG(u, v) + n(u, v), (u, v) e Z,

G ( u , v ) =

[ 0, ( u , v ) 6 Z ,

||% H ( u , v ) - ( %( u , v )|| < о - проектор на множество Е₆.

С учетом наличия шумов в изображении, решение обратной задачи с геометрической точки зрения можно интерпретировать как «размывание» области допустимых решений. Таким образом, пересечение выпуклых множеств в идеальном случае представляет собой точку, которая «расплывается» в некоторую область.

Следует также отметить, что этот алгоритм охватывает ранее предлагавшийся авторами для коррекции радиоизображения алгоритм Гершберга– Папулиса [Кузнецова и др., 1990], который может быть записан в компактной форме:

Этот алгоритм разрабатывался с несколько иных позиций, c использованием свойства аналитичности спектра ограниченной функции, т. е. он затрагивал только условия ограниченности функции и точной определенности ее спектра в ограниченной области. Как показали численные эксперименты, этих ограничений недостаточно, чтобы получить существенное улучшение радиоизображения. Только с введением новых ограничений удалось получить достаточное повышение качества восстановленного изображения.

Мы можем заключить, что алгоритм, состоящий из чистого проецирования на замкнутые выпуклые множества E1, …, E6 и реализованный с помощью итераций fk+i = Pffc, k = 0,1, ..., где P – композиционный оператор, составленный из проекторов Pi, i=1, …, 6, сходится к единственному решению, удовлетворяющему условиям 1–6.

Рисунок 2 иллюстрирует работу данного метода на модельном источнике.

а          б            в             г

:             I 1              1

Рис . 2. Восстановление модельного источника методом ПЗВМ : а – модель источника ; б – результат свертки с ДН ; в – результат восстановления без использования оператора P ₄ после 50 итераций ; г – результат восстановления с использо ванием оператора P ₄ после 50 итераций .

Существенным плюсом метода ПЗВМ является возможность включения в алгоритм обработки ряда типичных для солнечной радиоастрономии ограничений, таких как ограничения на поток, положительность, размер, и других ограничений, следующих из постановки физической задачи. Показано, что, если мы знаем дисперсию шума, в итерационный процесс возможно включить оператор проецирования P 6 , позволяющий стабилизировать итерации.

Выделение слабоконтрастных образований в солнечной короне

Практически все виды солнечной активности весьма эффективно проявляются в микроволновом излучении Солнца. Мониторинг солнечной активности, в том числе слабоконтрастных событий, систематически выполняется от восхода до захода Солнца на фоне солнечного диска в микроволновом излучении с высоким пространственным и временным разрешением на ССРТ с 1980-х гг. и радиогелиографе обсерватории Нобеяма (NoRH) [Fujiki, 1999] с 1990-х гг.

Радиогелиографические данные о слабоконтрастных образованиях содержат ценную информацию, необходимую для изучения условий возникновения, особенностей эволюции и прогноза солнечно-земных связей. При выявлении физических свойств корональных дыр, протуберанцев и волокон важна идентификация этих образований на солнечном диске. В микроволновом излучении она бывает затруднительна. Предложенные ранее эффективные средства идентификации требуют наблюдений Солнца с высоким пространственным разрешением на двух и более длинах волн, что не всегда возможно.

Для выделения слабоконтрастных событий в распределениях радиояркости солнечной короны на ССРТ был разработан алгоритм на основе модификации фильтра Винера–Тихонова (описанного в первом разделе) и высокочастотного контрастирующего фильтра [Кузнецова и др., 2007].

Выделение слабоконтрастных объектов на диске Солнца происходит в несколько этапов. На первом этапе обработки предварительная фильтрация помех производится:

• 1)    фильтрами, устраняющими помехи, которые связаны с неточностью калибровки коэффициента усиления и нулевого уровня каналов;

• 2)    медианным фильтром для устранения импульсных помех;

• 3)    фильтром низкой частоты для устранения шума за пределами полосы пропускания ССРТ с целью

обеспечения устойчивости решения обратной задачи. Далее изображение восстанавливается с помощью описанного выше фильтра Винера–Тихонова.

Параметры регуляризации фильтра выбираются в зависимости от отношения сигнал/шум и размеров исследуемой области. Повышение чувствительности изображения достигается путем усреднения карт радиояркости Солнца за 3–4 ч.

На втором этапе в полученном изображении удаляются яркие участки. Эта операция вводится для того, чтобы выделить участки с пониженными значениями яркостных температур, такие как КД и волокна. Отметим, что после осуществления этой операции задача отождествления волокон и КД не представляется тривиальной, поскольку яркостная температура волокна в наблюдаемом диапазоне составляет всего лишь 10 % от уровня спокойного Солнца, а КД меньше 6 % и на восстановленных картах радиояркости может присутствовать не полностью скорректированный процедурой восстановления тренд. Учитывая эти обстоятельства, мы не можем выделить волокна и КД простым вычитанием спокойного Солнца.

На третьем этапе происходит контрастирование источников с помощью высокочастотного фильтра, выполнение анализа полученных контурных значений и трактовка их как отдельно выделенных объектов.

Для контрастирования был использован градиентный фильтр Собела, позволяющий построить карту градиентов, при этом, в зависимости от задачи, возможно построение разных операторов оценки градиентов.

В общем случае использовался рекурсивный фильтр Собела. В задаче распознавания волокон, которые, как правило, представляют собой вытянутые с востока на запад области, применялся фильтр вида

H ( j , k ) = y ² .

После получения карты градиентов производится выделение областей с заданными пороговыми значениями. У волокон это значения, близкие к максимальному градиенту. У КД градиент обычно меньше, чем на границах волокон, и его определяют в коридоре меньших значений.

В результате описанной процедуры получаются прерывистые значения границ волокна или КД. Для устранения точечных или одиночных величин нами был использован медианный фильтр.

Следующим этапом является связывание точек контура, которое осуществляется на основе последовательной локальной обработки каждого пикселя. При таком анализе используются два основных параметра для установления сходства пикселей контура: величина отклика оператора градиента и направление вектора градиента. Первый параметр задается значением H ( j , k ). В этом случае пиксель контура, имеющий координаты ( j ₀, k ₀) и расположенный внутри заданной окрестности ( j , k ), считается сходным по модулю градиента с пикселем ( j , k ), если

H(j,k)-H(j0,k0 ≤E, где E – априори заданный порог.

Направление вектора градиента задается выражением

α ( j , k ) = arctg

( Y (j, k ) ^ I X ( j , k) J ‘

Пиксель контура с координатами ( j 0 , k 0 ), расположенный внутри заданной окрестности ( j , k ), считается сходным по направлению градиента с пикселем ( j , k ), если

α(j, k)-α(j0, k0) ≤ A, где A – априори заданный порог.

Пиксель в заданной окрестности объединяется с центральным пикселем ( j , k ), если выполнены критерии сходства и по величине, и по направлению. Этот процесс повторяется в каждой точке изображения с одновременным запоминанием найденных связанных пикселей при движении центра окрестности.

Примеры исходного распределения радиояркости, содержащего активные области и слабоконтрастные события, и восстановленного радиоизображения солнечной короны, демонстрирующего результат применения предложенного метода восстановления, приведены на рис. 3 и 4. На «грязной» карте (рис. 3, а)

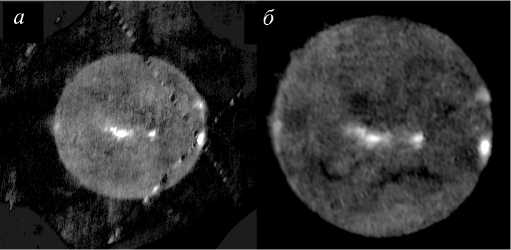
Рис . 3 . Исходное распределение радиояркости солнеч ной короны 11 мая 2006 г ., искаженное шумами и боковы ми лепестками ДН ССРТ ( а ) и восстановленное радиоизо бражение ( б ).

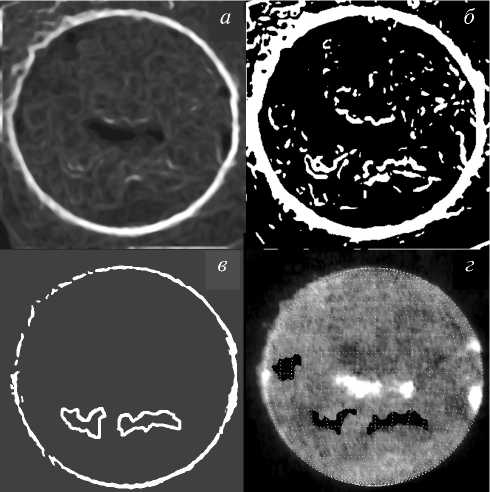
Рис . 4 . Идентификация волокон с помощью повыше ния контраста и выделения контуров слабоконтрастных событий в солнечной короне 11 мая 2006 г .: последова тельное выделение по градиентам ( а ), незамкнутых ( б ) и замкнутых ( в ) контуров , контрастное отображение ( г ).

Рис . 5. Изображения Солнца , полученные 11 мая 2006 г . на различных уровнях солнечной атмосферы .

видны искажения шумами и откликами в боковых лепестках ДН ССРТ, особенно от активной области, расположенной вблизи западного лимба солнечного диска. На восстановленном радиоизображении Солнца (рис. 3, б) за 11 мая 2006 г. наряду с яркими активными областями выделяются волокна (в южной части) и корональная дыра севернее активных областей в центральной части солнечного диска. Этапы контрастирования изображения представлены на рис. 4.

На рис. 5 приведены изображения Солнца, полученные 11 мая 2006 г. различными обсерваториями (построчно слева направо) на длине волны 5.2 см (ССРТ), 1.7 см (NоRH), 304 Å (SOHO/EIT), в мягком рентгене (GOES), Hα (обсерватория Big Bear), на λ=195 Å (SOHO/EIT), 1.82 м и 0.91 м (обсерватория Nancay). Они свидетельствуют о том, что слабоконтрастные образования в солнечной атмосфере прослеживаются и выделяются в хромосфере (Hα, 1.76 см, лучше на 195 Å и хуже на 304 Å), нижней короне (на ССРТ). Корональные дыры и волокна отчетливо видны в тепловом излучении (мягком рентгене) на GOES. Интересно отметить, что корональные дыры, видимые в мягком рентгене (GOES), хорошо прослеживаются в верхней короне на длине волны 0.91 м и не заметны на 1.82 м (Nancay). В то же время активные области одинаково отчетливо видны в хромосфере (за исключением Hα), нижней короне и короне, видимой в мягком рентгеновском излучении. Исключением является отсутствие восходящей АО и одной заходящей АО в Hα.

Такое проявление разномасштабных образований в излучении солнечной атмосферы на разных высотах свидетельствует о различной топологии локального магнитного поля, присутствии восточнозападной асимметрии солнечной активности, требует совместного изучения изображений Солнца, получаемых в различных диапазонах длин волн на различных уровнях солнечной атмосферы, и может дать новые знания о распределении параметров плазмы и топологии магнитных полей в атмосфере Солнца.

Заключение

В работе дан обзор методов восстановления и коррекции радиоизображений Солнца алгоритмами проекций на замкнутые выпуклые множества (ПЗВМ), модифицированным фильтром Винера–Тихонова, методом CLEAN. Применение созданных алгоритмов и программ продемонстрировано на примере изучения слабоконтрастных образований в солнечной короне (волокна, протуберанцы и корональные дыры).

Представленные методы были адаптированы для работы с данными ССРТ и показали свою эффективность. На основе метода ПЗВМ достигнута экстраполяция спектра пространственных частот за пределы полосы пропускания фильтра, что дает возможность повышения пространственного разрешения ССРТ при наличии априорной информации.

Предложенные алгоритмы могут быть использованы для анализа данных нового многоволнового радиогелиографа (4–8 ГГц), создаваемого в рамках проекта по модернизации ССРТ, а также других радиотелескопов высокого разрешения. Кроме этого, методы пригодны для исследования двумерных пространственных полей в таких областях науки и техники, как геофизика, океанология, медицинская томография.