МГД-эффекты, возникающие в экспериментах с вращающимся диском в присутствии осевого магнитного поля

Метод вращающегося диска является одним из основных инструментов исследования взаимодействий твердое тело - жидкость в физической химии расплавов и растворов, электрохимии, экспериментальной металлургии и пр. Широкое распространение он получил благодаря уникальному свойству потока жидкости, вовлекаемой диском в движение: толщина гидродинамического и диффузионного пограничных слоев одинакова вдоль поверхности диска. Равнодоступность поверхности диска в диффузионном отношении делает этот метод пригодным для количественной оценки параметров гетерогенных химических реакций, как это было показано в [1]. Книга [2] содержит многочисленные примеры использования метода в физической химии высокотемпературных расплавов - для изучения взаимодействия углерода с жидким железом.

Известны эксперименты по исследованию влияния внешнего магнитного поля на параметры взаимодействия твердое тело - жидкость, например, [3-5]. В [3] было обнаружено, что скорость растворения никеля в эвтектическом расплаве висмут-свинец изменяется в несколько раз в присутствии магнитного поля. В [4] показано, что скорость коррозии аустенитной стали в расплаве Pb-Li существенно уменьшается при появлении магнитного поля с индукцией примерно 0.4 Т, направленного перпендикулярно корродирующей поверхности. В [5] такое же заключение сделано в отношении коррозии упомянутой стали в растворе Fe-Cl3. В [3] считается, что магнитное поле непосредственно влияет на константу скорости растворения. Подобную точку зрения, однако, вряд ли можно обосновать с помощью фундаментальных принципов, учитывая гигантскую (для магнитного поля!) величину эффекта. Авторы [4] результаты своих опытов объясняют магнитогидродинамическими эффектами, приводящими к зависимости от магнитного поля толщины пограничных слоев на поверхности диска и, как следствие, к зависимости от этой причины интенсивности конвективного массопереноса. Эта, правильная на наш взгляд точка зрения, в [4], однако, количественно не обосновывается. В [5] тормозящее коррозию действие магнитного поля объясняется ссылкой на «микромагнитогидродинамические эффекты», физическая природа которых, однако, не разъясняется. Совершенно не ясно, например, в чем могли бы состоять подобные эффекты, если учесть, что жидкость в [5] (водный раствор Fe-Cl3) имеет электропроводность на многие порядки меньшую, чем жидкости, изучаемые в [3] и [4] (металлические расплавы).

Задача о течении, возбуждаемом в вязкой несжимаемой жидкости вращающимся диском (бесконечного радиуса), уникальна в том отношении, что допускает точное решение в полной нелинейной постановке. Это означает, что существуют такие преобразования зависимых и независимых переменных, которые приводят исходную краевую задачу для уравнений Навье-Стокса в частных производных к краевой задаче для системы обыкновенных дифференциальных уравнений. Впервые эти преобразования и решение задачи были указаны фон Карманом в 1921 г [6]. С тех пор задача Кармана интенсивно изучается, обобщается и используется при построении точно решаемых моделей реальных процессов во многих отраслях науки и техники, начиная с астрофизики и кончая теорией центробежных насосов. В работе [7] было показано, что преобразования Кармана возможны и в магнитогидродинамическом (МГД) случае, когда вдоль оси дис- ка, погруженного в проводящую жидкость, действует однородное и статическое магнитное поле. Эта возможность вскоребыла использована в связи с задачами геофизики в [8], где было показано, как магнитное поле влияет на создаваемое диском гидродинамическое поле. В [9] было замечено, что ввиду высокой электропроводности металлических расплавов МГД-эффекты становятся существенными уже в сравнительно небольших полях и при объемах образцов порядка тех, что используются в физико-химических экспериментах над жидкими металлами. В настоящей работе мы оценим, возможно ли с помощью МГД-эффектов объяснить результаты, полученные в [3] и [4] (но не в [5]).

Математическая формулировка задачи

Уравнения движения вязкой несжимаемой проводящей жидкости в присутствии магнитного поля имеют вид

^ + (W)V = - —VP--— V(B)² + — (BV)B + pAV,          (1)

at             p 2ц„р        pop

+ (VV)B = (BV)V + — AB.                       (2)

. at                       poa где V, P - поля скорости и давления в жидкости, В - индукция магнитного поля, р, а, и -плотность, электропроводность и вязкость жидкости соответственно, pQ - магнитная постоянная. Используем цилиндрическую систему координат с началом на поверхности диска и представим компоненты полей в (1) и (2) в виде

VT = rFtF^z^ Vv=raG^ уг = Мн^

Вт=тСК^ В^ = тС^ Вг=ВйМ^У(3)

Р = p^Vp^) + pvflq(z^, где Q - угловая скорость вращения диска, Во - осевая компонента индукции внешнего магнитного поля вдали от диска,

,X

1/2у

С = BQpQa (pQ) , zx = z —=—.

Тогда уравнения движения можно записать в виде (для стационарного движения):

F'" - HF" + 2GG' = —2агМК" + 4аг6 LL" ,

2FG + HG' -G" = 4аЧ KL^2a2ML’ ,

2Р + Я' = 0 ,(6)

MF' + К" = 6НК* ,

MG' + L" = 6HL\(8)

М" = 6^НМ'-МН^ ,(9)

М' + 25Я = 0 ,(10)

где 2 ° = 2^2 ’'

Если вдали от диска жидкость вращается с угловой скоростью Q1$ сам (непроводящий) диск - с угловой скоростью Qo, a Q - наибольшая из этих скоростей, то граничными условиями для уравнений (4)—(10) являются:

Р(0) = 0 ,  G(0) = % ,  Я(0) = 0 ;(11)

Р(оо) = 0, G(oo) = ^^ , Н(оо) = Н^ = const;(12)

#'(0) = 0,   ЦО) = 0,(13)

Я(оо) = 0,   Я(оо) = 0,   М(оо) = 1(14)

Они означают отсутствие проскальзывания жидкости на границе с твердой поверхностью и не-протекание электрического тока через эту границу, если твердое тело - диэлектрик. Отношение е = (Q_o - Qj) / Q, характеризующее относительную скорость вращения жидкости и диска, называется числом Россби.

Оценка параметров в уравнениях (4)—(10) показывает, что для жидких металлов 6 ~ 1(Г⁷ 4-10 ^s , а² - (1^100)х10² Bq /Q и поэтому можно считать 5 = 0, M(z) = 1. Используя это и некоторые соображения, высказанные в [9], окончательно краевую задачу можно сформулировать как:

В² - G² + HF* - F" = -2a² F -

(Q

2FG + HG' -G" = 2a² — , (QJ

2F + H' = 0, B^, + G = Q₁/Q К ' 4- F = 0

Очевидным преимуществом этой системы по сравнению с исходной является то, что гидродинамические переменные F, G, Н отделились от электромагнитных L, К в первых трех уравнениях. В них магнитное поле фигурирует только в виде параметра магнитного взаимодействия a.

Расчет поля скорости жидкости

Задача (11)—(19) представляет собой двухточечную краевую задачу для системы нелинейных дифференциальных уравнений в обыкновенных производных. Для решения подобных задач отсутствует теория, столь же развитая, как и для линейного случая (ввиду неприменимости принципа суперпозиции). Чаще всего в этой ситуации используют различные варианты метода стрельб (одно- или многократных)1 и релаксационные конечно-разностные методы.

Применительно к решению системы (11)—(19) метод одиночных стрельб подробно обсуждался в [9]. Хотя он сравнительно прост в реализации, однако не всегда эффективен в вычислительном отношении, особенно при больших значениях параметра магнитного взаимодействия. В настоящее время более широко применяются методы многократных стрельб и конечно-разностные. Задачи рассматриваемого типа нередко возникают в вычислительной практике, и алгоритмы их решения реализованы и содержатся в известной библиотеке IMSL fortran library: «метод многократных стрельб» реализован в подпрограмме BVPMS/DBVPMS, а конечно-разностный - в подпрограмме BVPFD/DBVPFD.

Подпрограмма BVPMS/DBVPMS уже была использована в [10] для расчета течений, возбуждаемых диском в бингамовской жидкости и в жидкости со степенным законом вязкости. Андерссон [11, 12] использовал подпрограмму из библиотеки NAG, основанную на том же алгоритме, предложенным Перейрой [13], что и подпрограмма BVPFD/DBVPFD, при решении задачи о жидкости со степенным законом вязкости (проводящей или нет). Для анализа эффективности используемого математического обеспечения и сравнения с ранее полученными результатами мы провели предварительные расчеты поля скоростей неньютоновской жидкости со степенным законом вязкости [11-12, 14] с помощь подпрограммы DBVPFD. В этом случае уравнения движения имеют вид [11-12]:

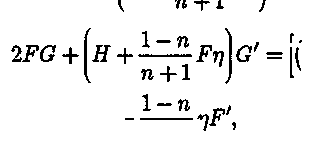
где 77 = г

о^2

к/р

\У(»+1)

(1-»)/(1+п)

- безразмерная координата, а граничные условия записываются

как:

F(0) = 0, G(O) = 1, Я(0) = 0,

F(oo) = 0, G(oo) = 0.

В таблице можно сравнить полученные результаты с таковыми, найденными ранее Андерссоном [ 11 ] и Мичкой и Ульбрехтом [14]. Здесь приведены граничные при 77 = О значения функций F', G ' и Н , отсутствующие в условиях (21) и относящиеся к жидкостям с различным показателем п в степенном законе для вязкости. Заметим, что если бы они были известны заранее, то вместо краевой задачи мы имели бы задачу Коши, методы решения которой хорошо разработаны. Из таблицы видно, что результаты, полученные нами с помощью подпрограммы DBVPFD, с высокой точностью совпадают с полученными ранее.

Сравнение граничных значений F', G ¹ и Н , полученных в настоящей работе, с результатами [11] и [13]

и	Р'ф)			-G'(0)			—Я(оо)
		[П]	[14]	[И]		[14]	[11]		[14]
1,5	0,5292	0,529	0,529	0,6010	0,601	0,601	0,6783	0,676'	0,678
1,3	0,5215	0,522	0,521	0,6035	0,603	0,603	0,7359	0,735	0,735
1,1	0,5139	0,514	0,514	0,6101	0,610	0,610	0,8221	0,822	0,819
1,0	0,5102	0,510	0,510	0,6159	0,616	0,616	0,8823	0,883	—
0,9	0,5069	0,507	0,507	0,6243	0,624	0,624	0,9688	0,969	0,958
0,8	0,5039	0,504	0,504	0,6362	0,636	0,636	1,0926	1,089	1,052
0,6	0,5004	0,501	0,500	0,6776	0,676	0,677	1,4602	1,364	1,351
0,5	0,5008	0,501	0,501	0,7136	0,712	0,713	1,6515	1,539	1,513
0,4	0,5038	—	0,504	0,7691	—	0,769	—	—	—

Для сравнения метода многократных стрельб с конечноразностным были проведены расчеты для системы (11)—(19) с использованием подпрограмм BVPMS/DBVPMS и ВVPFD/DBVPFD соответственно. Результаты расчетов показали, что подпрограмма BVPMS/DBVPMS позволяет получить решения в плоть до а = 1,0 при вычислениях с обычной точностью (BVPMS) и до а = 2,5 при вычислениях с двойной точностью (DBVPMS). В то же время подпрограмма BVPFD позволяет получить решение для любых а, в настоящей работе мы ограничились значением а = 5,0.

Результаты

После определения поля скоростей при данной индукции магнитного поля можно использовать рассуждения [1] для отыскания плотности массового потока к поверхности диска. Результат расчета представлен на рисунке, где показана нормированная плотность потока 92(a) = j(a) / ДО) как функция параметра магнитного взаимодействия а при различных значениях чисел Россби и Прандтля (Рг = Ре/Re = v/D}. Для жидких металлов Рт ~ 102 4-103 и поэтому перенос вещества в них происходит посредством конвективной диффузии уже при малых скоростях течения. Из рисунка видно, что магнитное поле способно полностью подавить массообмен и тем быстрее, чем меньше число Прандтля. Результаты экспериментов [3] были обсуждены в [9]. Обращаясь теперь к опытным данным [4], где условия таковы, что Re = 21 000, На = 130, получаем, что параметр магнитного взаимодействия a = На / V2fle = 0,63 . Судя по рисунку, уменьшение плотности массового потока в магнитном поле должно составлять 5-10% для чисел Прандтля в диапазоне 103—102. Это удовлетворительно согласуется с изменением толщины коррозионного слоя в центре диска (~ 20%), наблюдаемом в работе [4], особенно если учесть величину погрешности приведенных там данных.

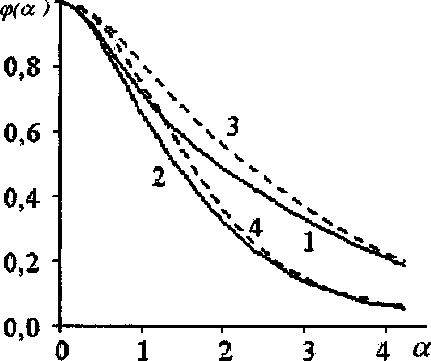
Влияние магнитного поля на плотность массового потока к поверхности диска:

1 - в= 1,0; Рг = 10’,2 - в= 1,0; Рг = 102, 3 -е= 0,1; Рг = 10’,4 - е= 0,1; Рг = 102

Заключение

Полученные результаты показывают, что МГД-эффекты способны существенно повлиять на кинетику массообмена между твердым телом и проводящим расплавом даже в условиях, реализующихся в обычных физико-химических экспериментах и при умеренных магнитных полях. Это дает возможность управлять с помощью магнитного поля интенсивностью массообменных процессов, совершенствовать технологические процессы с участием жидких металлов, а также создавать новые инструменты для физико-химических исследований, основанные на наблюдении МГД-эффектов.