MGF analysis of spatial diversity combiner over composite fading channel
Автор: Robert O. Abolade, Zachaeus K. Adeyemo, Isaac A. Ojedokun, Samson I. Ojo
Журнал: International Journal of Information Technology and Computer Science @ijitcs
Статья в выпуске: 10 Vol. 11, 2019 года.
Бесплатный доступ
The worldwide acceptability of wireless communication is due to its portability and flexibility. However, its performance is governed by the multipath propagation effects which make wireless communication modelling challenging. The existing technique being used to solve this propagation effects is based on Probability Density Function (PDF) which is inefficient in addressing diversity over combined Rayleigh and Rician (C_(Ray-Ric)) fading due to its complexity. Therefore, this paper aims to develop an approximated Moment Generating Function (MGF) for spatial diversity combining such as Equal Gain Combining (EGC) and Maximal Ratio Combining (MRC) over C_(Ray-Ric) fading channel. A MGF model in form of Taylor’s series is generated from the expected value of the C_(Ray-Ric) fading channels. The MGF is characterized using Amount of Fading (AF) and Bit Error Rate (BER) in term of Line of Sight (LOS) component ‘k’. The MGF is transformed into EGC and MRC, and were measured in terms of propagation paths (L). These are approximated using the Pade ́ Approximation (PA). The approximates obtained are used in the derivation of BER expression of M-ary Quadrature Amplitude Modulation (MQAM) and M-ary Phase Shift Keying (MPSK) in terms of Signal to Noise Ratio (SNR). The models are evaluated using AF and BER at different values of LOS to determine the performance of the diversity techniques. The results obtained show that as LOS component ‘k’ increases from 0, the Af and BER reduce indicating reduction in fading effects. Therefore, the models developed are effective in predicting the performance of diversity techniques and overcome the multipath effects associated with the wireless communication.
MGF, Rayleigh, Rician, Pade ́ Approximation, BER
Короткий адрес: https://sciup.org/15016391
IDR: 15016391 | DOI: 10.5815/ijitcs.2019.10.03
Текст научной статьи MGF analysis of spatial diversity combiner over composite fading channel
Published Online October 2019 in MECS
Wireless communication has become a worldwide phenomenon which transcends race, gender and religion. Its acceptability is due to its portability, flexibility, cost effectiveness, instant and easy connectivity with anyone, anytime, anywhere, convenience, and enhanced efficiency [10, 24, 25, 27]. However, it suffers from multipath fading effects, which are due to the effects of propagation mechanisms leading to multiplicative distortion. This eventually causes fading at the receiving end and has been previously solved using diversity techniques. The analysis of the diversity combining has relied so much on the Probability Density Function (PDF) based method which leads to multiple integrals and therefore, very complex to solve [23].
Diversity combining has been known to be a classical and a very powerful technique to address the multipath fading. In diversity, multiple copies of the signal which are independent, identically distributed are transmitted over different paths. This technique is exploited in space, time, frequency, and polarization. Space diversity is the most common form of diversity which is achieved using multiple antennas at the receiver. For diversity combining to be effective multiple signal copies need to be independent, hence, different types of diversity are efficient in different situation [2, 5, 21].
Wireless communication, (WC) can be modelled using different types of models namely: empirical, deterministic and stochastic models. Empirical model is based on field measurement obtained from results of several experimental efforts. This model is simple and efficient but depends on the terrain profile where the measurement is taken and therefore, is geographically bias. The deterministic model, on the other hand, is an analytical way of estimating propagation loss in wireless communication. There are two approaches in this deterministic model namely: solving some electromagnetic (e.m) wave equations, which is extremely complicated and the other one is the ray tracing approach, which is the most widely used but requires a lot of computing power. While in stochastic modeling, the wireless environment is treated as a series of random variables using statistical distributions and methods to characterize the wireless communications channel. Modelling of satellite communication which is a form WC has depended solely on several models such as Corraza, Loo and Lutz’s models, the latter is regarded as the best model for satellite channel but has too many parameters to be determined in the analyses [1, 8, 12, 14, 17, 18, 22, 23].
In [19], an investigation into the performance of M-ary Phase Shift Keying (M-PSK) in Mobile Satellite Communication (MSC) over combined ionospheric scintillation and flat fading channels with Maximal Ratio Combining (MRC) diversity was carried out. The paper focused on the derivation of the average Bit Error Probability (BEP) of M-PSK modulation scheme. In the paper, the satellite channel was modeled as a product of two Rician channels ( Rician X Rician Channels). This is because the signal passes through the ionosphere which consists of specula components and the lower atmosphere called the troposphere resulting in a product fading channel, also, due to reduction of Rician fading distribution to Rayleigh distribution when the Rician factor is zero. [9, 12, 13, 15, 16] have modelled various communication channels using moments based statistical approach. The work of [9] is on derivation of the Moment Generating Function (MGF) of the Weibull channel employing the well-known moments of the Weibull Random Variable (RV) and then expresses the MGF in term of a power series through the expected value operator, the infinite series is then approximated by Pad ́ Approximation (PA). Through this, analysis of the performance of digital modulations over Weibull slow flat fading channel is carried out. This paper addresses the stochastic modelling of wireless communication channel as a combination of Rayleigh and Rician fading ( ^Ray-Ric ) channel.
The rest of the paper is organized as follows: section II deals with review of the past related work, while section
III deals with modelling of the channel with the combining techniques as well as Pade Approximation (PA) and the Bit Error Rate (BER) of the composite fading channel. Section IV discuss the result obtained, while section V gives the conclusion of the paper.
-
A. Contributions
This paper has contributed to modelling of satellite communication channel which does not involve multiple complicated integrals and the suggested channel to model the satellite communication with simplicity and accurate.
-
II. Related Work
In [18], performance of M-ary Phase Shift Keying (MPSK) in Mobile Satellite Communication (MSC) over combined ionospheric scintillation and flat-fading channels with Maximal Ratio Combining (MRC) diversity was investigated. The paper identified the effect of combined scintillation and terrestrial fading at the lower atmosphere which resulted in a product fading channel and consequently, has a negative effect on the performance of the system. The authors identified the challenge of evaluating probability of error as a parameter to study the performance of the system. The research proposed MRC diversity as a means of mitigating the effect of the product fading channel which was modeled as the product of two Rician channel. In the work, Bit Error Probability (BEP) of MPSK over the product fading channel with MRC diversity was analyzed. Moment Generating Function (MGF) was employed and this resulted in a double summation integral in terms of the generalized hyper-geometric function. The result of the simulation revealed a significant improvement on the BEP and the BEP decreased as the diversity order increased. The developed BEP is rigorous and complex for further analysis.
Also, in [8] the use of Pade Approximation (PA) for performance evaluation of MRC diversity over Weibull fading channels was developed. In the research, the MGF of the Weibull channel was derived by employing the well-known moments of the Weibull RV and then expressed the MGF in terms of a power series through the expectation operator, the infinite series was then approximated by PA. Through this approximation, a comprehensive study of the performance of digital modulations over Weibull slow flat fading channel was carried out. The accuracy of the PA technique was illustrated by comparing the results of the exact MGF with Monte Carlo simulations. With the approximate expression, the performance of digital modulation schemes over single channel and multi-channel employing MRC was analyzed. The result showed an excellent agreement with previously published results as well as with simulations. The Weibull multipath fading channel cannot be used to model the satellite communication channel which the current research model as composite Rayleigh and Rician distribution.
Furthermore, in [12], Bit Error Rate (BER) analysis of Binary Phase Shift Keying (BPSK) modulation in a
Rician fading co channel interference was investigated. In this work, a precise BER expression was derived for a Rician-faded BPSK signal in the presence of Rician faded interfering signals. The research focused on using three approaches namely; characteristics function, Chernoff bound and saddle point approximation approach. The BER expression derived in Rician faded channel using the CHF approach requires two-fold integral and the expression is cumbersome for further analysis. The current research derives a simple Amount of Fading and BER expression over the combined Rayleigh and Rician distribution.
-
III. Modelling of Channel and Diversity Combining Technique
According to [1] and [19], CRyy _R,c fading channel has been proposed for modelling Flat or Frequency Non-Selective Mobile Satellite Communication channel. Assuming a combined Rayleigh and Rician fading channel in a communication system with either MRC or EGC receiver. The received signal r , (t) on each branch over a flat fading channel in the presence of noise is expressed as
Г (t) = a^t) + n , (t) (1)
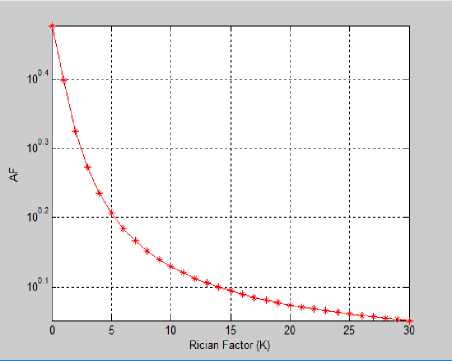
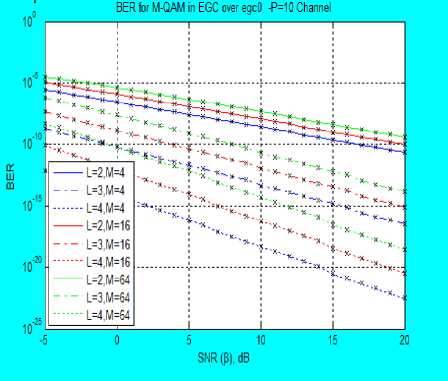
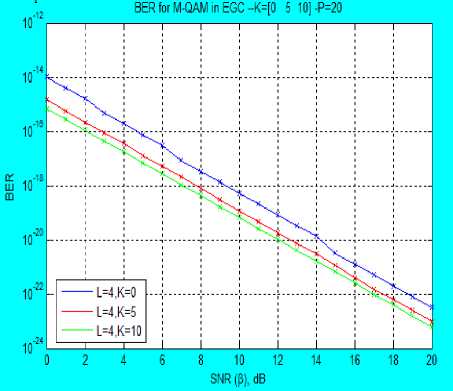
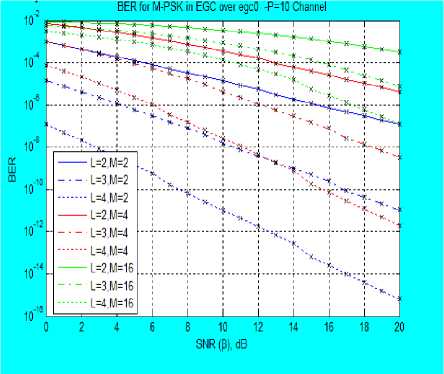
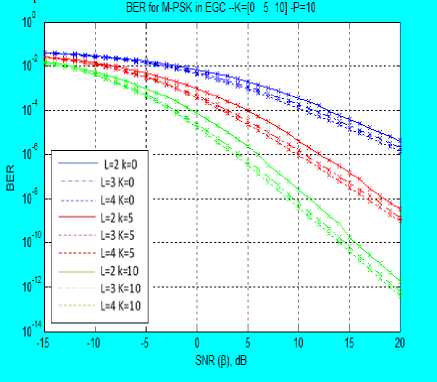
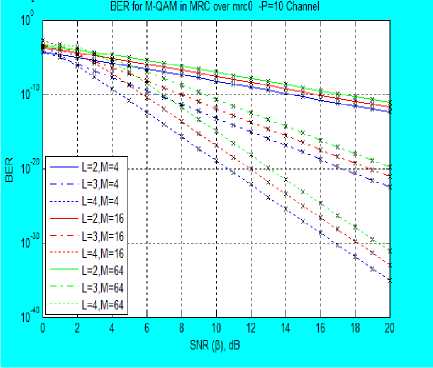
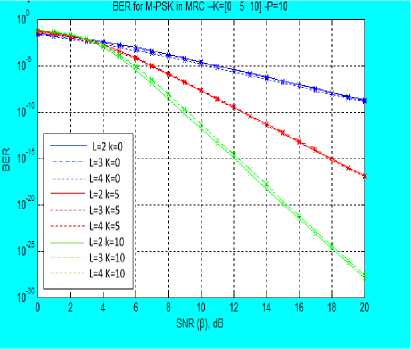
where s(t) is the transmitted signal, while for EGC, the weighted sum is given in (3) as r (t) = (ZL г R )2 (3) where w, is the weight of the lth branch and is given as the complex conjugate of c, R, is the fading envelope of lth branch. From [1, 7, 18, 23], the moments of MRC and EGC output are derived for the combined Rayleigh and Rician Fading channel as (E(P")C)L = (g^) ft (- n; 1; k ) p " ) X (K/Т 1)/ E (P"g a = ^Э^2 2F1 (-n; 1; -k)P’2n where P is the average SNR at the output of the combiner. A. Amount of Fading (AF) The AF can be statistically modelled from the moment and for any arbitrary combining technique, AF does not change. The moments derived are used to calculate the Amount of Fading (AF), AF is given in [23] as A F = ^L-1 У?№)2 This implies that AF requires only the first and second moments to determine its expression, upon finding the E [p2] and F[p], AF model is simplified to . Г2 (3^ (2;1 кй _ (2^1 (_1;1;_fcz))2 Equation (7) gives the AF model for the composite fading channel irrespective of the combining methods used. B. MGF of the Output of the Combiner MGF is a simple and powerful statistical tool for simplifying the analysis of diversity receivers. The nth moment of a random variable is the coefficient of the power series expansion of the MGF. This makes it so powerful in statistical analysis of the wireless communication channel. MGF is regarded as the Laplace Transform (LT) of the Probability Density Function (PDF) of a random variable and therefore, known as a complement of the PDF [23, 28]. It is expressed by [7, 18, 22] as Mp (s)=E{A^} = J” esp Pp(P)dP P>0 (8) Using (4), (5) and (8) with the Taylor series equivalent of the MGF which is given as MP (s) = ^ o5^ (9) With equation (9), the MGF series at the output of MRC receiver is given as MpMRC (s) = E”= 0 ^^n 2^1 (-n; 1; -kt)Y" (10) where Y = s 2 and Mp (s) is for a single channel, and I = 1, 2, ^. L and for L>1 and since this paper considers independent and identical distribution (iid) fading channel, then, Y = sД2, where P, is the average output SNR, therefore, (10) becomes MpMRC(S) = (2”=о;ГЙ772Л (-n; 1;-fci)Kn)L (11) while for EGC, MpEgc(s) = E”=oL^.^2 22F1 (-n; 1; -k,)/" (12) These two MGFs form an infinite power series in “s” and are not guaranteed to converge for any practical use. The uncertainty in its divergence or convergence is solved by employing PA. Therefore, the MGF series generated at L = 2 and k = 0 are given in (13) and (14) Мрмкс (s)=1+у2 +4е3у4+36у6 +576у8 + 1․44е4у10 + 5․18е5у12 + 2․54е7у14 + 1․65е9у16 + 1․32е^у18 + 1․32е13у20 + 1․59е13у22 + 2․29е17у24 + 3․88е19у26+7․6е21у28 + 1․71е21у30 + 4․38е26у32 + 1․27е29у34 +4․1е31у36 +1․5е34у38 + 5․92е36у40․ MpEGC (S)=1+4у+32у2+384у3 + 6․14е3у4 + 1․23е5у5 + 2․95е6у6 + 8․26е7у7 + 2․64е9у8 + 9․51е10у9 + 3․81е12у10 + 1․67е14у41 + 8․04 е15у12 + 4․18е17у13 + 2․34е19у14 + 1․40е21у158․99е22у16 + 6․11е24у17 + 4․40e26yi8 + 3․34е28у19 + 2․68 … C. Pad ́ Approximation (PA) A compact rational approximation of (13) and (14) is desirable to capture the limiting behavior of the power series. Therefore, in this paper, MGF is approximated in a rational form for subsequent computation. The one-point PA of order (Л⁄в), where A is the highest power of the polynomial in the numerator, while B is the А denominator, that is Рв (Z), defined from the series as a rational function by [4], [12], [13], [15], [16] and [26] as р§ (У)=∑в ° b j =∑п-о ^пУ '1 (15) ∑j=0 DP The coefficient at and bj are real coefficients defined such that ∑N =∑1=0^ =∑A+? 4- p(^.4+8+1 ) = =∑ + ( ) (16) where R( yA+B+1 ) represents the terms of order higher than A+B which is the remainder after the truncation by PA. The coefficients at and bj are obtained using the moment matching approach introduced by [3]. This is carried out by matching the coefficients of the power series on both sides of the equation above. Taking 60 =1 and without any loss of generality, equation (15) forms a set of equations obtained as follows, from (16), and neglecting the remainder, R( yA+B+1 ) , cross multiplication yields ∑ zlo СЦУ1 =∑ ^bjy1 ×∑n=0 ^пУ 0≤l≤В (17) The set of equations developed from (17) form a system of B linear equations for the B unknown denominator coefficients. This set of equations is solved using matrix method and back substitution in order to determine the coefficients at and bt . As a demonstration of this unique approximation technique, the MGF of the combined channel, Mp (s) without diversity at k = 0 which implies a combined Rayleigh-Rayleigh fading channel is Mp(s)= 1-s̅ This is similar to the well-known MGF Rayleigh expression given in [23] but differs because of the combined fading channel involved. D. Bit Error Rate of Diversity Combiner over Combined Fading Channel The BER of MPSK and MQAM over the combined fading channel for MRC and EGC diversity combiners are derived as follows: the approximated model from the MGF series for branch ‘L’ = 1, when there is no diversity is , l-24y+177y2-444y3+274y4 R(У)=------------------------ w 7 1—25y+200y2—600y3+600y4—120y5 Using the expressions given by [20, 23] with the PA approximated MGF series of the type in equation (19), the performance of digital modulation techniques M-PSK and M-QAM schemes can be obtained. In MRC, for an iid with the same fading parameters and the same average SNR per bit for all ‘L’ branches then the BER for M-PSK expression is derived as Pbmrc(E)=7tlog2 ∫ ) (Mp(Sin2∅ )) d∅ ^bmrc (E)= ∫ 4"m)Rmrc (У)d∅ (20) TCLOy2‘v* u Rbmrc(E)= 1 (1—)л 1-14․lly+61․96y2—95․38y3+39․03y4 ∫ M -----------------------------------u∅ л1од2^ J() 1-15․lly+75․69y2—152․71y3+119․16y4-27․02y5 while for EGC technique, the BER for M-PSK is given as; ^begc (E)= 1 ∫( 1м) 71 Mp ( -9PS )d∅, 9 тг1од2^∅ = ∫( 1 M) Regc (У)d∅ nlog2M Jo VV 7 where 9psk=sin2Л⁄м , and S= У=̅ y Sin2 ∅ Rbegc (E)= ___1 (1—)7Г l-96y+2․83e3y2-2․84e4y3+7․01e4y4 , (A 7ilog2M∫) l-100y+3․2e3y2-3․84e4y3+l․54eSy4-l․23esy5 ∅ The BER expression for MQAM signaling scheme with MRC, is given as лЬод2М (1√5)[∫ / 2 = м3 ( -gQ. )d∅-(1- L) ∅ √ ∫/ *Mp (~8Q1 )d∅․ ) p \ Sin2∅․ ×] where s=-Sqam , and Sm2∅ = ( ) =- ( ) p„ лЬод2М(1-√@)*∫ /Rmrc(У)d∅- (1- =)∫ ” / Rmrc (У)d∅+․ p. = 1 bmrc 4(1- лЬод2М V 1 )*∫ ⁄2 1—14 ․ lly+61 ․96y2-95․ 38y3+39․ °?y _ =d ∅ √M/ 1Л 1-15․lly+75․69y2-152․71y3+119․16y4-27․02y5 (1- )∫ /4 ․ lly+61 ․96y2-95․ 38y3+39․=d∅ √ )Jo 1-15․lly+75․69y2-152․71y3+119․16y4-27․02y5 . In case of EGC with M-QAM signalling scheme, the BER expression is obtained as p„ Htog2M(1-√5)*∫ / Rrgc (У)d∅-(1-√м)∫ / Rrgc (У)d ∅+ l-96y+2․83e3y2-2․84e4y3+7․01e4y4 l-lOOy+3․2e3y2-3․84e4y3+l․54e5y4-i․23e5y5 IV. Results and Discussion The AF and BER values obtained for the M-PSK and M-QAM signaling schemes over the combined Rayleigh and Rician fading channel using MRC and EGC at the receiver are presented in Figures 1-6. Figure 1 presents AF versus specular component K over combined Rayleigh and Rician fading channel. The amount of fading (AF) at the Rician factor, K, the LOS component К=0, is 3, while atк=30, the AF reduces to 1.127. This is true in real life scenario, at к=0, the fading model is completely a product of two Rayleigh fading channels. It also implies that there is no line of sight component between the transmitter and the receiver due to natural and man-made barriers. This result also shows that as the value of K increases, the AF reduces as expected in real life scenario. Fig. 2 presents the BER versus SNR using 4-QAM, 16-QAM and 64-QAM signaling scheme for EGC over the ^Ray-Ric fading channels with К=0dB . The results show that at SNR of 2dB, with two paths (L = 2), BER of 2․24×10”7 , 1․93×10-6and 1․04×10“5 are obtained for 4QAM, 16QAM and 64QAM respectively, while BER of 2․31×10-15 , 5․35×10-13 , 6․16×10-11 were obtained respectively at L =4 . This shows that BER reduces as the number of path ‘L’ increases. Fig. 3 depicts the BER versus SNR for L = 4 using 4-QAM scheme over ^Ray-Ric fading channel, at SNR of 2dB, BER values obtained are 7․32×10-13, 1․14×10-13 and 4․62×10-14 k = 0, 5, and 10 respectively, while at SNR of 15dB, 1․47×10-18 , 6 ․03×10-19 and 2․81×10 19 are obtained respectively. This shows that as K increases, the BER reduces and therefore, the performance improves with higher values of ‘k’. Fig. 4 presents the BER versus SNR using BPSK, QPSK and 16-PSK signaling schemes over ^Ray-Ric fading channel at different values of ‘L’ for k = 0. From Fig. 4 the BER values obtained at SNR of 3 dB with two paths (L = 2) are 2․87×10-4 , 0․00352 and 0․007319 for BPSK, QPSK and 16-PSK respectively, while 1․1×10-6 , 3․91×10“5 and 1․292 × 10“3 are obtained at SNR of 15 dB respectively. Also for L = 4, at SNR of 3 dB, BER obtained are 8․× 10“9, 1․04×10“5 and 1․649 × 10"3 for BPSK, QPSK and 16-PSK respectively. This shows that as the constellation increases, the BER values decreases as ‘L’ increases showing the advantage of combining nature of the paths. Fig. 5 depicts the BER versus SNR with EGC over ^Ray-Ric fading channel using BPSK at k = 0, 5, 10. At SNR of -10 dB, BER values of 0.01692 and 0.000239 are obtained for k = 0 and k = 10, respectively, while BER decreases at higher ‘L’. Fig. 6 presents the BER versus SNR using M-QAM schemes with MRC techniques. It can be confirmed that at SNR of 0 dB, with L = 2, 0.000115, 0.00074 and 0.001366 are the BER values obtained for 4-QAM, 16-QAM and 64-QAM, respectively at k = 0, while BER reduces at higher propagation path ‘L’. Also, in Fig. 7, BER values are presented against SNR over ^Ray-Ric fading channel with MRC at k = 0, 5, 10 for different paths. It can be deduced form the figure that at SNR of 5 dB and L = 3, 0.00043 and 0.000262 are the BER values obtained at k = 0 and 10 respectively which improves as SNR increases. The result obtained are justifiable in that when the value of k = 0, it implies total obstruction of the LOS indicating Rayleigh fading which is the worst case channel. As ‘k’ increases indicate appearance of LOS which reduces the BER value and therefore, the effects of fading. In terms of modulation schemes used, higher constellation means higher data rate which reduces the symbol period but invariably increases the Inter Symbol Interference (ISI) distortion. Fig.1. AF versus Rician factor K (dB) over the combined Rayleigh and Rician fading channel Fig.2. Bit Error Rate of 4-QAM, 16-QAM and 64-QAM modulated signals versus SNR over EGC over Rayleigh and Rayleigh product fading channel (K = 0 dB) Fig.3. Bit Error Rate of 4-QAM modulated signal versus SNR over EGC over Rayleigh and Rician fading channel for different values k = 0, 5 and 10 Fig.4. Bit Error Rate of BPSK, QPSK and 16PSK modulated signal versus SNR over EGC in Rayleigh and Rayleigh product fading channel (K = 0) for different values of L Fig.5. Bit Error Rate of QPSK modulated signal versus SNR over EGC over Rayleigh and Rician product fading channel for different values of K and L Fig.6. Bit Error Rate of 4-QAM 16-QAM and 64-QAM modulated signal versus SNR over MRC in Rayleigh and Rician product fading channel (K = 0 dB) Fig.7. Bit Error Rate of BPSK modulated signal versus SNR over MRC over Rayleigh and Rician product fading channel for different values of K and L V. Conclusion An approximated MGF based models for EGC and MRC diversities over CRay-Ric fading channel has being developed using M-QAM and M-PSK signaling schemes. MGF channel models obtained are approximated using PA in ^Ray-Ric channel for EGC and MRC. Expression for performance metrics for M-QAM and M-PSK schemes have being derived at different Rician factor k and different propagation paths L. The technique is simulated using wireless standard parameter with MATLAB simulation software and evaluated using AF and BER expressions developed. The AF results obtained show that as Rician factor k increases AF reduces, but when k = 0 indicates worst case because it will result in Rayleigh and Rayleigh fading channel where there is total obstruction of the signal path. Also, lower constellation of the modulation schemes gives lower BER values than the higher constellation schemes due to their higher rate which increase the ISI. Therefore, an approximated MGF based models over CRay-Ric channel has been carried out using PA. The models developed is simple to solve with single integral and has being able to avoid multiple complex integrals of the PDF models. It has also been able to show that the MRC and EGC are effective technique in mitigating the adverse effect of multipath fading.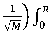
Список литературы MGF analysis of spatial diversity combiner over composite fading channel
- Adeyemo, Z.K., Ojedokun, I.A. and Akande, D.O ‘Symbol Error Rate Analysis of M-QAM with Equal Gain Combining over a Mobile Satellite Channel’ International Journal of Electrical and Computer Engineering, 2013, 3 (6): 849-856,
- Alouini, M. and Goldsmith, A.J. A ‘Unified Approach for Calculating Error Rates Linearly Modulated Signals over Generalized Fading Channels’ IEEE Transactions on Communications, 1999, 47 (9): 1324-1324.
- Amindavar H. and Ritcey J.A. ‘Padé Approximation of Probability Density Functions’ IEEE Transactions on Aerospace and Electron System, 1994, 30 (2): 416-424.
- Brennan, D. ‘Linear Diversity Combining Techniques’ Procedure of. IRE, 1959, 47 (6):1075-1102.
- Goldsmith, A., ‘Wireless Communications, (3rd ed.) Cambridge University Press, 2005.
- Helstrom C.W., “Probability and Stochastic Processes for Engineers”, Second Edition, Macmillan, New York, USA, 1991.
- Ippolito, L.J., “Satellite communication system engineering: Atmospheric Effect, Satellite link Design, and System Performance,” (1st ed.) John Wiley & Sons, Singapore, 2008.
- Ismail, M.H. and Matalgah, M.M. On the Use of Padé Approximation for Performance Evaluation of Maximal Ratio Combining Diversity Over Weibull Fading Channels EURASIP Journal on Wireless Communications and Networking, 2006, 3(1):62-68.
- Jochen S., Mobile Communications. (2nd ed.) Pearson Education Ltd., India, 2006.
- Kale, S.S. and Jadhav A.N. An Empirically Based Path Loss Models for LTE Advanced Network and Modeling for 4G Wireless Systems at 2.4 GHz, 2.6 GHz and 3.5 GHz, International Journal of Application or Innovation in Engineering & Management (IJAIEM), 2013, 2 (9): 252-257.
- Karagiannidis G. K., Sagias N. C., and Zogas D. A., “Error analysis of M-QAM with Equal Gain Combining diversity over generalized fading channels”, IEE Transactions on wireless communications, 2005, 152 (1):69-74.
- Karagiannidis, G. K., “Moments-Based Approach to the Performance Analysis of Equal Gain Diversity in Nakagami-m Fading,” IEEE Trans. Commun., 2004, 52 (1):685-690.
- Loo, C., “A Statistical Model for a Land Mobile Satellite link” IEEE Transactions on Vehicular Tech., 1985, 34 (3):122 – 127.
- Malhotra J., “Investigation of M-QAM and MPSK with EGC in Generalized Flat Fading channels”, Journal of Advances in information Technology, 2011, 2 (4):250-256.
- Malhotra J., Sharma A. K., and Kaler R. S., “On the performance Analysis of Wireless receiver using generalized-gamma fading Model”, Annals of Telecommunications, 2009, 64 (1):147-153.
- Mishra A.R., “Second generation network planning and optimization (GSM)”, John Wiley and sons, New Jersey, 2004.
- Papoulis, A. Probability, Random Variables and Stochastic Processes, McGraw-Hill Inc. New York City, USA, 1991.
- Pornchai, S., Wanaree, W., and Sawasd, T., “Performance of M-PSK in Mobile Satellite Communication over Combined Ionosphere Scintillation and Flat Fading Channels with MRC Diversity”, IEEE Transactions on Wireless Communications, 2009, 8(7):3360-3364.
- Proakis, J. G., “Digital Communications”, McGraw-Hill companies, Inc. International Edition, 2001.
- Ramanathan, V. Performance Evaluation of Equal Gain Diversity Systems in Fading Channels, Unpublished M. Sc. Thesis, Virginia Polytechnic Institute and State University, USA, 2003.
- Rappaport T. S., “Wireless Communication Principles and Practice” Communication Engineering and Emerging Technologies Series, second edition, Prentice, Hall of India Private limited, New Delhi, 2002.
- Simon, M. K., and Alouini, M.S., “Digital Communication over fading channels” John Wiley & Sons. Inc. Hoboken, New Jersey, 2005.
- Stallings W “Wireless Communications and Networks,” 3rd Indian Reprint Pearson Education Ltd., India, 2003.
- Stuber, G. L., “Principles of mobile communications,” (2nd ed.), Kluwer Academic publishers New York, 2002.
- Suetin, S.P. Padé Approximants and Efficient Analytical Continuation of a Power Series, Russian Mathematical Surveys, 2002, 57 (1):43-141.
- Tse, D., and Viswanath, P., “Fundamentals of Wireless Communication” (1st ed.) Cambridge University Press, New York, 2005.
- Yilmaz F., and Alouini M., “A Unified MGF-Based Capacity Analysis of Diversity Combiners over Generalized Fading Channels” IEEE Transactions on Communications, 2010, 10(20):1-26.


