MIMO Capacity Analysis Using Adaptive Semi Blind Channel Estimation with Modified Precoder and Decoder for Time Varying Spatial Channel
Автор: Ravi kumar, Rajiv Saxena
Журнал: International Journal of Information Technology and Computer Science(IJITCS) @ijitcs
Статья в выпуске: 10 Vol. 4, 2012 года.
Бесплатный доступ
Multiple Input Multiple Output(MIMO) has been in much importance in recent past because of high capacity gain over a single antenna system. In this article, analysis over the capacity of the MIMO channel systems with spatial channel with modified precoder and decoder has been considered when the channel state information (CSI) is considered partial. Due to delay in acquiring transmitted information at the receiver end, the time selective fading wireless channel often induces incomplete or partial CSI. The dynamic CSI model has also been implemented consisting channel mean and covariance which leads to extracting of channel estimates and error covariance which then further applied with the modified precoder and decoder utilizing both the parameters indicating the CSI quality since these are the functions of temporal correlation factor, and based on this, the model covers data from perfect to statistical CSI, either partially or fully blind. It is found that in case of partial and imperfect CSI, the capacity depends on the statistical properties of the error in the CSI which has been manipulated according to the precoder and decoder conditions. Based on the knowledge of statistical distribution of the deviations in CSI knowledge, a new approach which maximizes the capacity of spatial channel model with modified precoder and decoder has been tried. The interference then interactively reduced by employing the iterative channel estimation and data detection approach, where by utilizing the detected symbols from the previous iteration, multiuser/MIMO channel estimation and symbol detection is improved.
MIMO Capacity, Blind Channel Estimation, Semiblind Channel Estimation, Partial CSI, Spatial Channel
Короткий адрес: https://sciup.org/15011765
IDR: 15011765
Текст научной статьи MIMO Capacity Analysis Using Adaptive Semi Blind Channel Estimation with Modified Precoder and Decoder for Time Varying Spatial Channel
Published Online September 2012 in MECS
MIMO antenna systems is an advanced technique for high data rate transmission over frequency selective fading channels due to its capability to combat the intersymbol interferences (ISI), low complexity, and spectral efficiency. Also it increases the multiplexing gain (i.e. throughput) and diversity gain (i.e. robustness) of communication system in fading channels. It has been shown that for any given number of antennas, there is a fundamental tradeoff between these two gains and works on space-time architecture had focused on maximizing either of these two gains.
However, recent works have proposed space-time architecture that simultaneously achieves good diversity and multiplexing performance. This increase in capacity is enabled by the fact that in rich scattering wireless environment, the signals from each individual transmitter appear highly uncorrelated at each of the receive antennas. When conveyed through uncorrelated channels between the transmitter and receiver, the received signals responds to each of the individual transmitter antenna to separate the signals originating from different transmit antennas.
Spatial multiplexing examples are given in [1] . It obtains high data spectral efficiencies by dividing the incoming data into multiple streams and transmitting each stream using different antenna. At the receiver end, these streams are separated by various techniques as given in [1] .
The gains obtained by implementing of multiple antennas at both sides of the link can be characterized by the array gain, diversity gain and the multiplexing gain. By combining the information signal on multiple transmit or multiple receive, there is an improvement in signal to noise ratio (SNR) which is to be known as Array gain which has been generalized for low SNR system whereas improvement in link reliability by obtaining different replicas of the information through different fading environment gives us the diversity gain which is generalized for high SNR systems.
These two gains are not exclusive for MIMO systems, whereas meant for single input multiple output (SIMO) and Multiple input single output (MISO) too. On the other end, spatial multiplexing is generalized for MIMO specifically which increase the rate at no additional power and bandwidth consumption.
The multipath characteristic of the environment causes the MIMO channel to be frequency selective for higher data rate transmission. Due to the unique feature of OFDM for converting a frequency selective channel into a parallel collection of frequencies, the receiver complexity is reduced. The MIMO-OFDM provides a very promising system for enhancing the capacity and improving the link reliability for future broadband wireless communication. However to obtain the promised capacity and to achieve maximum diversity gain, MIMO-OFDM system require accurate channel state information (CSI) at the receiver, in order to perform coherent detection, space-time decoding, diversity combining, and the spatial interference suppression.
When using multiple antennas, the coherence distance represents the minimum distance in space separating two antennas such that these experience independent fading. Due to scattering environments, the channel exhibits independent or spatially selective correlated fading which results in lower achievable capacity of MIMO. In MIMO-OFDM systems, channel estimation based on either least squares (LS) or minimum mean square error (MMSE) methods, has been widely explored and several estimation schemes have been proposed [2, 3] . Channel estimation based on adaptive filtering proposed in [4] with modified precoder and decoder gave an appropriate solution for estimating and tracking the time-varying channel in mobile environments.
The article is distributed in different sections as follows. In section 2, multipath wireless channel has been shown for time varying channel. In section 3, MIMO constant channel capacity has been shown for multipath fading systems corresponding to ease in analysis. In section 4, evolution of partial channel state information derived from perfect channel state has been discussed for MIMO systems. In section 5, the system model has been considered using MIMO channel system. In section 6, implementation of proposed estimation scheme has been shown with modified precoder and decoder in the MIMO system. Further section 7 and 8 comprises the discussion of results and conclusion over the complete capacity analysis of MIMO systems using modified precoder and decoder.
-
II. Wireless Multipath Channel Model
In a complex wireless communication system, a signal transmitted in a channel interacts with different type of environment like there are reflections from large objects, diffraction of the electromagnetic signals in the case of moving of mobile systems. The result of these complex interactions is the presence of multipath signals at the receiver end.
Earlier channel models depicts only the information about signal amplitude level distribution and Doppler shifts of the received signals which were designed for narrowband systems only. [5] .
With time after facing many phases of advances, the system become more complex and accurate like additional algorithms and time delay spreads.
Figure.1 represents a Radio frequency(RF) channel as a time varying channel and using a baseband complex envelop representation, the channel impulse response for mobile systems 1 has been represented as [6]
L(t)-1 jφ (t)
h(t,τ) =∑ A (t)e l,1 δ{t -τ (t)} l=0 l,1 l,1
where, L ( t ), A , φ , τ , θ & δ ( t ) denotes the number of paths, amplitude, carrier, phase shift, time delay and angle of arrival (AOA), direc delta function of t for the l th signal component of the K th mobile user. Here the amplitude has been generalized as Rayleigh distribution random variable and the phase shift has been considered as uniformly distributed.
A measure of the time rate of change which is also known as the time varying nature caused by the motion of the objects of the channel is the Doppler power spectrum which was given by M.J.Gans in 1972 [5] . This power spectrum gives us the statistical information of the variation of the frequency received by mobile station at some velocity. Gans assumed with reference to the flat fading channel model given by R.H.Clarke in 1968, that the mobile station receives the signal from all directions in a uniformly distributed manner.
The AOA of each multipath component has not been considered in channel model given by (1). The AOA can be included in the vector channel impulse response using
L ( t ) - 1
h ˆ l ( t , τ ) =∑ A l ,1 ( t ) ej φ l ( t ) a ˆ( θ l ( t ) δ ( t - τ , ( t )) (2)
where, a ˆ( θ ( t )) is the array response vector which is a function of array geometry and AOA. This equation gives the spatial channel impulse response which is a summation of several multipath components, each of which has its own AOA, phase and amplitude. The distribution of these components is totally dependent on the types of the environmental conditions.
In this paper, the wireless model has been chosen based on MIMO antenna array system assuming sufficient antenna element spacing so that the subchannel between different transmit receive antenna pairs are spatially uncorrelated, and have channel impulse response (CIR) of equal maximum resolvable path L. Each subchannel is assumed to be slowly time varying frequency selective fading so that it can be considered as a constant during one OFDM symbol. The time variant complex baseband CIR between the
M T transmit and the N R receive antenna can be described as
L-1
hMT,M (τ,t)=∑ βM ,MR(l)δ(t-τl) (3)
where, β ( l ) and τ represents the gain and the delay of the path l , respectively. The path gains β ( l ) are modeled as independent and identically distributed
(i.i.d.) wide sense stationary (WSS) complex Gaussian random variables with zero-mean and variance σ 2 [7] . They are represented as
j ( θ l + 2 π f d , l t )
βMT,MR ( ) = MT,MR ( )e
where, A ( l ), θ , and f denote the amplitude, phase and Doppler shift of the lth path, respectively.
A0,1(t)ejφ0,1(t)δ(t-τ0,1)
Stable Interference
Mobile system 2 Capacit
Mobile system 1
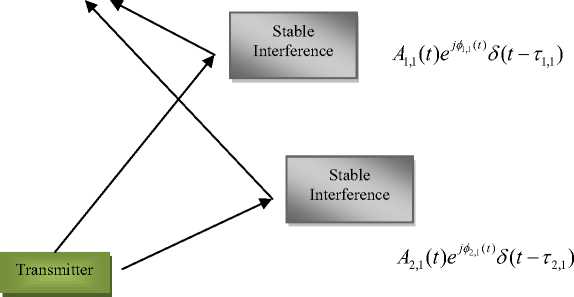
Fig.1: RF channel as a time varying channel
Assuming isotropic scattering, the autocorrelation of the path gains is expressed as rl(τ) =E{βl(t)*βl(t+τ)} =σl2Jo(2πfDmaxτ)(5)
where, σ 2 is the power of the l th path gain, J ( x )is the
Bessel function of the first kind of order 0, andis
, the maximum Doppler frequency which is related to the velocity ν of the movement and the wavelength λ of the carrier frequency by fDmax =ν/ λ.
It is known that spatial channel model(SCM) has been widely designed for urban microcell, urban macrocell and suburban macrocell fading environment simulations. It considers N cluster of scattering medium, each corresponds to a resolvable path. Within a resolvable path, there are M irresolvable subpaths. [8]
For a MT element linear base station(BS) array and a MR element linear mobile station(MS) array, the channel coefficient of one of the N multipath components are given by a M R x M T matrix of complex amplitude. Assuming omni-directional antenna element at the BS and MS and neglecting pathloss and shadowing, the CIR for the l th path between the M transmit and M receive antenna can be written as
R
MT , MR
( t ) =
P M '
l ∑ exp[ j ( kd M sin θ m ', n ', AOD ) + φ M , M M ' m '=1
× exp[ j ( kd M sin θ m ', n ', AOA )
× exp[ jk || V ||cos( θ m ', n ', AOA θν ) t ]
where, j =-1 , k is the wave number 2π/λ, λ is the carrier wavelength in meters, p is the power of the l path, M ' is the number of subpaths per path, d is the distance in meters from BS antenna element M to the reference (s=1) antenna, d is the distance in meters from MS antenna element M to the reference (u=1) antenna, ||v|| is the magnitude of the MS velocity vector, θ is the AOA for the m ' subpath of the n' path with respect to the BS broadside.
-
III. Constant MIMO Channel Capacity
When the channel is constant and known perfectly at the transmitter and the receiver, Telater [9] showed that the MIMO channel can be converted to parallel, noninterfering SISO channel through a singular value decomposition (SVD) of the channel matrix. Waterfilling the transmit power over these parallel channels whose gains are given by the singular values ст,2 of the channel matrix, leads to the power allocation

where, P is the power in the i eigenmode of the channel,( x )+ is defined as the maximum of (x,0) and w ' is the waterfill level. The channel capacity is shown to be
C = Z{log (w ст2)} (8)
The worst case of additive noise was Gaussian which has been shown in [10] given by Diggavi, where the worst case noise is also given for low SNR too. An algorithm to compute the worst case noise for any SNR is obtained in [11] . Although the constant channel model is relatively easy to analyze, wireless channels in practice typically change over time due to multipath fading.
-
IV. Capacity with Partial Channel State Information
There has been much evolution in the capacity of multiple antenna systems with perfect Channel state information at receiver(CSIR) i.e. reliable estimation at the receiver but only partial Channel state information at transmitter (CSIT) i.e. timely feedback of the channel state to the transmitter. For multiple antenna systems, the capacity improvement using partial CSIT is under research by so many researchers like Madhow and Visotsky [12] , Trott and Narula [13, 14] , Jafar and Goldsmith [15-17] , Jorswieck and Boche [18, 19] and Simon and Moustakes [14, 20] .
A full rank matrix is required to generate optimum input covariance matrix which can be incorporated in vector coding across the antenna array. Beamforming can be made by limiting the rank of the Input covariance matrix as unity which leads to scalar system which has a significant lower complexity for typical array size. The optimality of beamforming using scalar codes to achieve good enough capacity with enough CSIT captures the tradeoff between the complexities and capacity and still is the topic of research. It is known that vector coding refers to fully unconstrained signaling schemes for the diversified MIMO Gaussian channel. This channel corresponds to the input to each transmit antenna as the vector symbol and the receiver take into account the dependencies for these vector codewords in both space and time dimensions, hence increasing the complexity of vector decoding exponentially with the increase in the number of transmit antennas. It has been shown in [15] that lower complexity implementation of the vector coding strategy is possible by transmitting several scalar codewords in parallel, without the loss if capacity. It is required to see the transmitter optimization and the optimality of beamforming in the MIMO systems. When a MISO channel is considered whose channel matrix is rank one, with perfect CSIT and CSIT, it is possible to identify the non-zero eigenmode of the channel accurately and beamforming along the mode. Whereas with no CSIT and perfect CSIR, Foschini and Gans [21] and Telatar [9] showed that optimal input covariance matrix is a multiple of identity matrix hence the power is equally distributed in all directions. Visotsky and Madhow [12] numerical results indicate that beamforming is close to the optimal strategy when quality of feedback improves. Also Narula and Trott [22] showed that there are cases for mean feedback conditions where the capacity is actually achieved via beamforming for two transmit and receive antenna. A generalized form for optimality of beamforming was given by Jafar and Goldsmith [16] for both cases of covariance and mean feedback.
With MIMO antenna systems, the covariance feedback case with correlation at transmitter is solved by Jafar and Goldsmith [17] whereas Jorsweick and Boche [19] implemented the fade correlation at the receiver also. The mean feedback case with multiple transmit and receive antennas was solved by Jafar and Goldsmith in [15] and Moustakas and Simon in [20] . These solution have been found for the condition where the channel mean has rank one [15] and two [20] . It has been shown that the channel capacity grows linearly with minimum number of antennas either at transmitting or receiving side by Foschini and Gans [21] . This linear increase occurs whether the transmitter knows the channel perfectly (perfectly CSIT) or doesn’t know the channel at all (no CSIT). This has also been shown in [9] .
Now for the case of mobile receivers which experiences rapid fluctuations of channel coefficients may face the problem if reliable channel estimation. In wireless communication, user mobility is the principle driving force, for which partial CSIT and CSIR is of particular interest.
MIMO capacity in the absence of CSIT and CSIR was earlier given by Marzetta and Hochwald [23]. They generated the model of the channel matrix components as i.i.d. complex Gaussian random variables that remains constant for a coherence interval of T symbol periods after which they change to another independent realization. They showed that for a fixed number of antennas, if the length of the coherence interval increases, the capacity approaches the capacity obtained as if the receiver know the propagation coefficients. More importantly, under the perfect CSIR assumption and in the absence of CSIT, capacity doesn’t increase with the increase in number of antenna beyond the length of the coherence interval T. MIMO capacity then further analysed by Zheng and Tse [24] in the absence of both CSIT and CSIR and showed that at high SNRs, the optimal strategy is to use no more than
M** = min { MT , MR ( T /2) } transmit antennas i.e.
increasing transmit antenna than the receive antenna doesn’t provide any capacity increase at high SNR and also at each 3 dB SNR increase, the capacity gain is
M T
*
1 -
M T
*
T
Further Lapidoth and Moser [25] compared with the Zheng and Tse model for block fading [23, 24] and showed that without the block fading assumption, the channel capacity in absence of CSI grows only double logarithmically in SNR. The discussion in [23, 24] left a little hope of achieving high capacity gains for MIMO systems when receivers are highly mobile. It is known that in severely fluctuating channel, it is difficult to achieve reliable channel estimation whereas on the other hand, it is much easier to estimate the distribution of channel fades which changes very slowly than the channel itself. This estimated distribution can be used as the feedback controlling channel for the transmitter to work more efficiently.
Cui and Tellambura in [26] have discussed about the Maximum-likelihood(ML) semiblind gradient descent channel estimator which detects the semiblind data for Rayleigh and Rician channel exploiting the channel impulse response. Feng and Swamy in [27] derived the blind constraint from the linear prediction of MIMO-OFDM with the weighting factor in the semiblind cost function. Abuthinien, Chen and Hanzo in [28] proposed a joint optimization with repeated weighted boosting search of unknown MIMO channel and ML detection of the transmitted data. Expectation maximization algorithm for single carrier MIMO using overlay pilots has been proposed by Khalighi in [29] . Rather than using real input signals, complex input signals have been analyzed by Yu and Lin in [30] using forwardbackward averaging method in semi blind channel estimation of space time coded MIMO with zero padding OFDM. Advantage of periodic precoding, block circulant channel model design after cyclic prefix removal and optimal design of precoding sequence has been done by Sheng in [31] for the robustness of the channel estimation w.r.t. channel order overestimation and identification ability of full rank matrix. Analysis of second order statistics of the signal received through sparse MIMO channel exploiting the most significant taps(MST) of the sparse channel forming the correlation matrices of the received signal has been done by Feng in [32] . Better Bit Error Rate (BER) has been tried recently by Kyeong in [33] by designing new iterative extended soft recursive least square(IES-RLS) estimator for both joint channel and frequency offset estimation. Recent work [26-33] has shown the analysis of Mean Square error(MSE) and BER generally without the discussion over capacity analysis, which has been discussed in this paper.
By using these channel correlations, the channel matrix components are modeled as spatially correlated complex Gaussian random variable that remains constant for a coherence interval of T symbol period after which they change to another independent realization based in the spatial correlation model. It is shown by Jafar and Goldsmith [34] that the channel capacity is independent of the smallest MT-T eigenvalues of the transmit fade covariance matrix as well as the eigenvectors of the transmit and receive fade covariance matrices QT and QR. By looking into the results for the spatially white fading model where adding more transmit antenna beyond the coherence interval length(MT>T) doesn’t increase capacity. Jafar showed that increase in transmit antenna always increase capacity as long as their channel fading coefficients are spatially correlated. It has been shown that with the channel covariance information at the Transmitter(Tx) and Receiver(Rx), transmit fade correlations can be beneficial in the condition of highly mobile and inaccurately measurable fast fading channel by minimizing the spacing between the antenna. It has been shown by an example that with coherence time T=1, the capacity with MT transmit antennas is 10 log M dB higher for perfectly correlated fades than for independent fades.
-
V. System Architecture
E '
If it is assumed that the system is having lossless feedback i.e. CSIT and CSIR both are same. Thus 22
H , Rr , R , c ■& C represents that the CSI is known to both the ends. With the partial CSI model, the channel output can be considered as y = tlx + E' x + n with the total noise given by E' x + n with mean zero and covariance matrix given by
R = E '^ ( Ex + n )( Ex + n ) |
= E ' [ R R /2 E m R T1 ( - )( C ) HE H ( R R /2) H ] + c IMr
= c 2lr ( R T Q ) R R + c „2 I M
where, the expectation is w.r.t. the distribution of x, n and E' . It is known that n is not Gaussian and it is not to i easy to obtain the exact capacity equation. Thus tight upper and lower bounds can be taken in consideration for system design. The mutual information with partial CSI for unpredictable capacity with Gaussian distribution can be denoted as iL
I u = I l + log2 | R n | - E '{ log2| R( x H R r x ) R r + c „ 2 I m„ | } (12)
I & I , denote the lower and upper bounds on the maximum achievable mutual information with the error E ' considered over the distribution of x .
Since the information is passing through the parallel subcarriers for the system with covariance matrix Q is given, the achievable rates are given as
C.= (C .-CU where, K denotes the number of users,
E C kn ' - B N lo g 2 det k
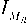
E hQhH +—----- N' Bn.
where, B is subcarrier bandwidth, Q is the covariance matrix and N ' is total number of subcarriers. The capacity of uplink region with all subcarriers and users will then become
C = (C1, then, (13) states that
Qkn> 0, k = 1,.....K, n' = 1,.....N;,(14)
tr (Qkn,) - Pk, k = 1,......K(15)
n '=1
where, P is the power constraint for K users and (15) shows the inequality of the uplink individual power constraint. It is known that (14) and (15) can be formulated with the following total power constraint which will provide us the downlink channel capacity using the uplink capacity region as given above.
KN '
EE tr (Q^ - p k=1 n' =1
K where, P = E P is the downlink power constraint. k=1
Here, (11) for capacity lower bound has been considered for design criteria as has been considered in [36] . To obtain the highest data rate using the capacity lower bound [37] i.e. to get the best estimates out of all received data estimates, the following problem is required to be solved [36] ,
, - max Й>»,ег№<Рт
1°§2 тмк +
HOH
cr>(Rg)R +cr„2/
where, the lower bound on the Ergodic capacity is CL = E [ Il ] with the expectation w.r.t. the fading channel distribution.
Alternatively a common detection strategy for frequency selective MIMO channels is to achieve temporal equalization first and then spatial equalization [38] . Temporal equalization can be easily found using blind equalization methods based on second order statistics (SOS). These SOS based blind equalization schemes achieve temporal equalization while leaving the ambiguity of an instantaneous combination which is equivalent to a narrowband MIMO system. The narrowband MIMO channel matrix can be denoted by H = [ h ] for 1 - M „ - N„ and 1 - Mt - NT ,
MR,MT R R T T , where hM,M denotes the non-dispersive channel coefficient linking the M transmitter to the M receiver. In this scenario, a slow fading environment has been considered for remaining all the entries unchanged in the MIMO channel matrix H at the time of transmitting block or frame. The channel impulse response hM,M assumed to be i.i.d. complex valued
Gaussian variable with zero mean and E| \Mmt,Mr |l — 1- The modulation scheme considered is M-QAM and the values from the defined M-QAM symbol set as
X'j = [ x '(1) x '(2) X '( J ) ] as the available training data. The channel estimation of the MIMO channel H using least square method relies upon { Z ( J ), X '( J ) } which gave us,
With the real part symbol R [ Sf 9 J = u = 2 i — MX — 1
and the imaginary part symbol
I [ S i , q ] = u q = 2 4 — V M — 1 . The average SNR of the
Д ' h ' ' h 1
H = ZjXj I хлхл )
system is defined as
S / N = N x cts 2 /2 ^ 22
An spatial filter bank or equalizer are used to detect the transmitted symbols S for 1 < MT < NT .
y MT ( к ) = u M r x ( K ), 1 < Mt < Nt (20)
where, и мis the Nr x 1 complex valued weight vector of the mth spatial equalizer. The MMSE solution for the N T spatial equalizer considering the channel to be perfectly known can be shown by
MMSE , MT
HHH + -2l In„ ^
—1
hMT ,
1 < MT < N (21)
where, h denotes the m th column of the channel matrix
H. It is known that in spatial domain, the short term power is applicable i.e. No temporal power allocation can be considered. On the other hand it is know that the power constraint is applicable across each antenna at each fading state for a given H ˆ . The expectation of mutual information over fading channel distributed can be maximized by maximizing the mutual information [39] i.e.
max E [ I т ] < E
Q > 0, tr { Q } < P t
max I
Q > 0, tr { Q }, P t
Here, the right hand side is the maximum value which can easily be achieved with short term power constraints and with the partial channel state information.
VI. Proposed Scheme
When the transmitter is considered for both spatial pre-filtering matrix and power allocation, the mutual information of the MIMO system corresponding to nth subcarrier is given by [40] ,
( H ( n W n ) P ( n ) ro H ( n ) HH ( n ) 1
I ( y ( n ); x ( n )) = log det j Im, + ( ) ( ) (2 -(-)(-) I (23)
L R n mt J
where, co ( n ) & P ( n ) is the spatial pre filter matrix and power allocation. Assuming the pilot symbols be J which can be denoted as Z3 = [ Z (1) Z (2)..... Z ( J ) ] and
and noise variance is arrived by this equation is
* n = JMZ — HHx J ir (25)
R
It is required to have training pilots as low as possible, for which { Z ( J ), x '( J ) } should have full rank. To achieve this, choosing J = max { MT , MR } = MR i.e. assuming J = M R which can be treated as the lowest number of pilot symbols.
The MMSE solution gave the spatial equalizer weight vectors using roughly estimated value H ˆ of channel,
C A 2 1
Vmt = I HHH + —^IMr I hr Mt , 1 < Mt < Nt (26)
X ^s / where, hˆ denotes the mth column of the estimated channel matrix Hˆ . The weight vectors (26) are not sufficient to estimate correctly because the pilot symbols are in sufficient. An adaptive estimation method has been utilized from [4] since it was not easy to use direct decision adaptation.
Unknown estimate sequence a has been determined in [4] to avoid sacrifice of tracking ability of channel. Also the minimum path metric with its short time average of long detected sequence i.e. ц к was detected using the average of long detected sequence i.e. ц к was detected using the adaptive recursive method proposed which has been utilized to calculate the minimum branch metric ц к for all possible estimated vectors for tracking surviving state with minimum value of channel coefficients H ˆ as shown in Figure.2. Further the weight vectors in (26) of mth spatial equalizer is updated at each step with increase in processing steps k . It was seen that the value of p in the marginal PDF associated with weights is to be maintained under proper limits near 1 so as to identify the estimates properly since it is related with variance.
The capacity analysis after enhancing the estimate perfection, which leads to get the optimized covariance matrix Q for which we assume an adaptive precoder and decoder( A , B ) at the transmitter and receiver end. A and B are MT x r and r x MR matrices with r = rank ( HI ).
Let x x 1 a zero mean i.i.d. unit variance data vector. Then x = A.D and Q = E ( xxH )= AA H . From Figure.3,
we have y = HAD + n = HAD + EAD + n and then received vector after the decoder is given by R = B.y. Defining the MSE matrix(A,B) with expectation w.r.t. s, n and E, as
ЛЖАВ)=I^((R DXR Di'7]
=E {в(Я+Е)А-^}1И У х|в(Я+Е)А-^ {^
+^BR
To reduce the MSE, (17) can be written as
min ln MSE(A, B)
A,B , tr { AA h } < P T
Finding the optimized solution for (17) is related with the optimized solution of (28) with a global maximum existing for (17) and global minimum existing for (28).
= ВЯААяЯяВя - ВЯА - АяЯяВя
+ Л, + В {^-(RAA")R + ^IMR } Вя
where, B { ° 2 tr (RAA H )R + a n IM^ } B H is R nT .
Fig.2: Proposed channel estimation method with reducing pilot symbols with increase in iterations
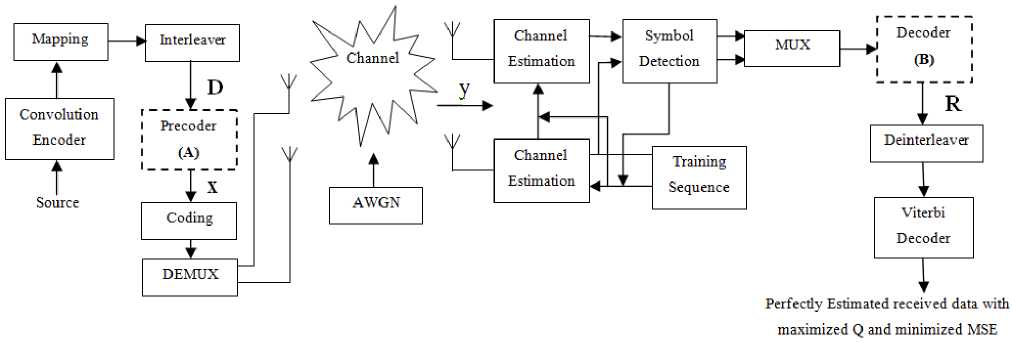
Fig.3: Blindly Estimation of transmitted symbols using the MIMO systems with Modified Precoders and Decoders
With partial CSI, the minimum MSE design minimizes the trace of the MSE matrix whereas on the other hand the maximum mutual information minimizes its log determinant, which is the capacity lower bound achievable with a Gaussian input distribution. [41]
An optimized precoder and decoder pair may be obtained by solving and satisfying the Karush-kuhn-tucker(KKT) which will also satisfy the condition A U , UH B ' where U is an arbitrary x x x unitary matrix and A ' & B ' are the optimized pair set.
According to KKT condition, the Lagrangian can be considered as
S [ ( A j , B j ) Kj= p д '] = MSE + д'
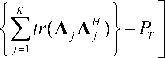
min min tr [ MSE { A , B ( A ) } J (30)
A , tr ( AA H )< P T B ( A )
The minimizing B for the inner unconstrained minimization is shown as where, д' is the Lagrange multiplier associated with the sum power constraint
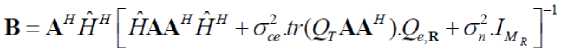
min
A , tr ( AA H )< P T
Which is the linear MMSE data estimator with given H ˆ and A [42] . Here Q and Q are the covariance matrices for the transmitter and receiver. Substituting (31) in (30), the problem in (28) can be formulated as
tr [ MSE ( A ) ]
Where,
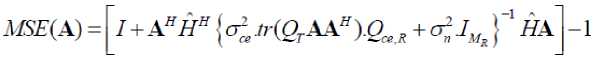
The feasible set of (32) is {a | tr ( AA H ) < PT } , a
Frobenius norm of radius P . The objective function of (32) is continuous at all points of the feasible set. According to Weierstrass theorem [43], a global minimum for (32) has been evolved which also exists for (28). Based on (30),(31),(32) and (33), the associated KKT condition can be found as
^ =в,(унЛА"н^°1-1«,
7=1
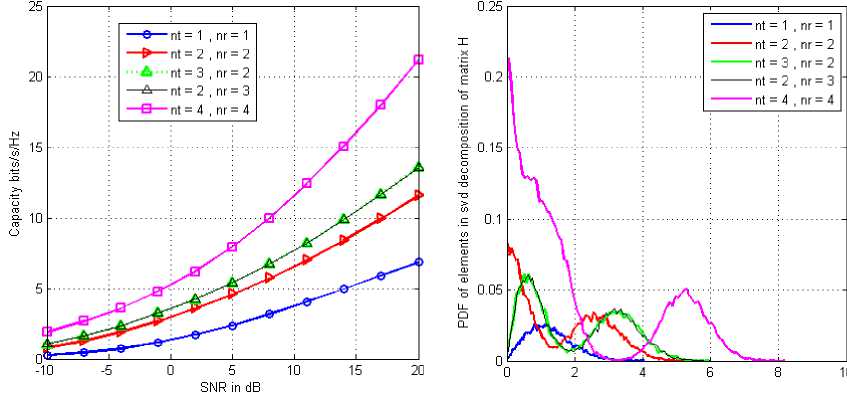
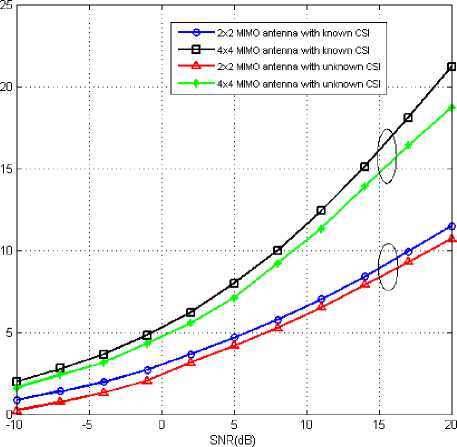
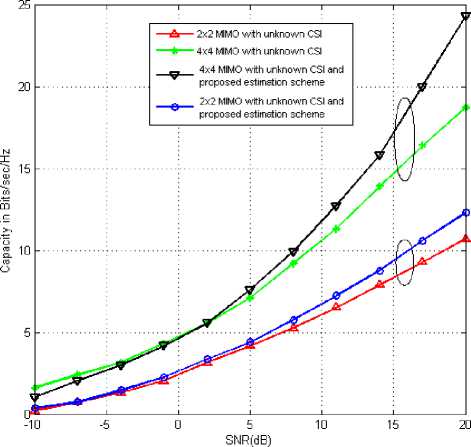
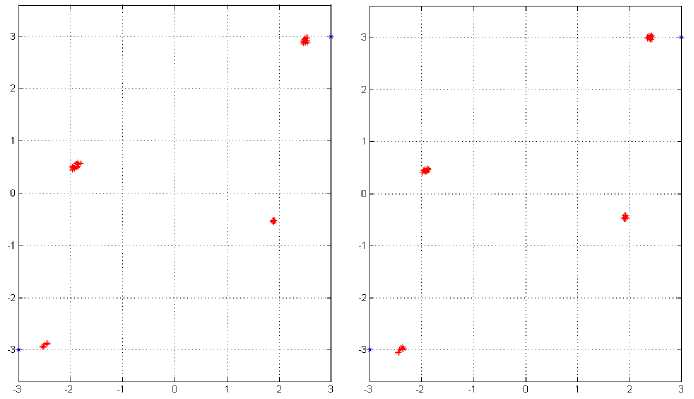
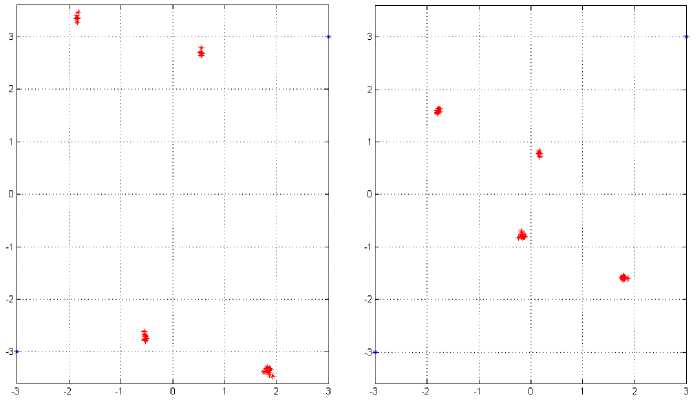
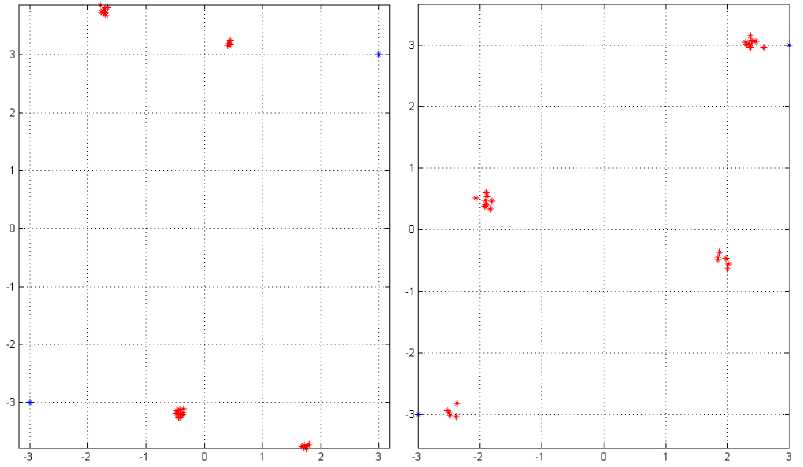
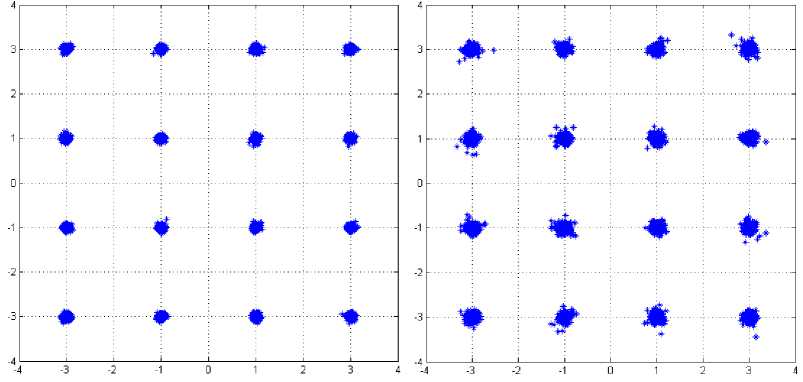
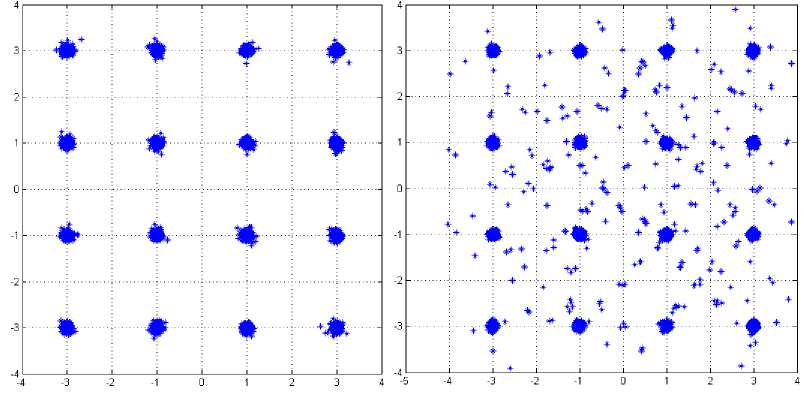
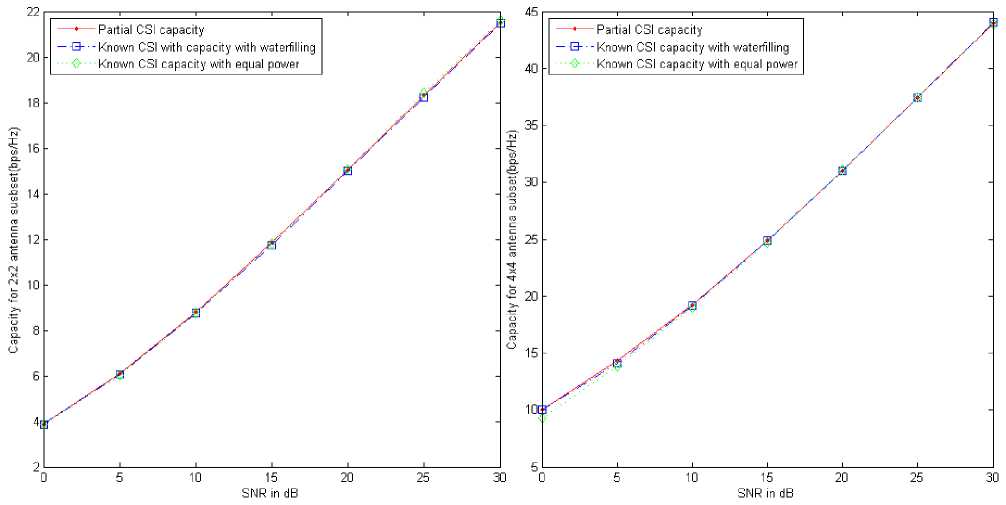
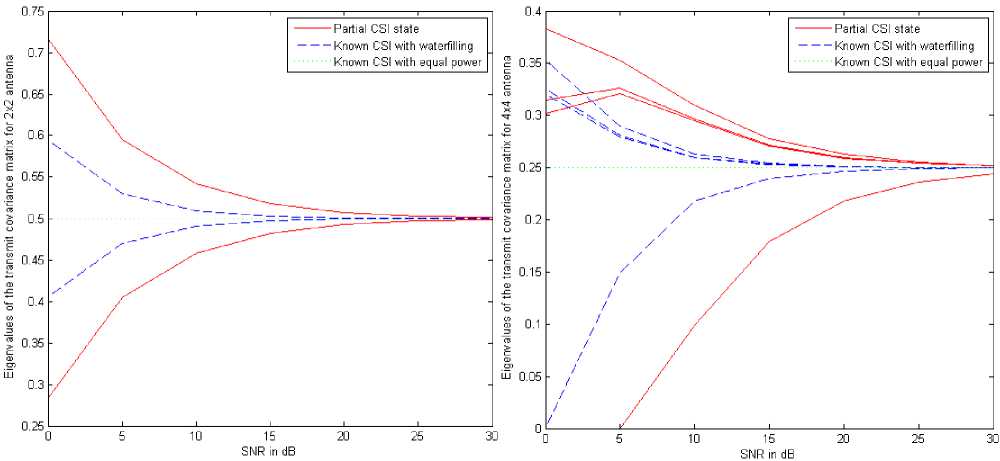
+f д >0, £tr(A,AH) decoder satisfying the KKT condition hold the following identity K Д = (^п/ Pt )£ tr (BкBK ) (38) k=1 The algorithm based on the condition (34)(35)(36) (37), is shown in table 1. Table 1: 1) Initialize A^,k = 1,....K, satisfying the power constraint with equality and are non zero. 2) Update B using (34), for k=1,….K. 3) Update д using (38), 4) Update A using (35) for k=1,…..K. 5) If the termination condition is met, stop; otherwise go back to step (2) till practical convergence. Based on the above method, (27) can be formulated to find the optimum structure of the A and B, д. ^ £ tr(Aj AjH ).Pt ^ = 0 A' aEa R + д/мг У ^VФ A (39) Since the objective and constraint functions of (28) are continuously differentiable w.r.t. A,B and the feasible point of (28) satisfy the regularity condition [43] and the global minimum should satisfy the first order KKT conditions associated with (28). With these properties, it is concluded that the KKT conditions are necessary for local and global minimum both. The relation between Lagrange multiplier and receive В'=ФвV[^EaR + д!мт ]■ 5 x HIH [a2tr (RA'A'H) R + ^2Imr ] where, ФА = [Ir -Л-1J2 (41) Фв =[Ir -Л-1]Л-1 (42) And, a = tr B'R ‘ст2tr (RA'A'H)R + ct„'IMJ-‘ X HA ' (43) 6) If ||A. - AM || < s, stop; otherwise go back tostep 2 until practical convergence. ц = ^^ tr [b' {ctEtr(RA'A'H )R + ст,IMr }"‘ x H.A'] (44) Matrix V and Л are defined by the following eigenvalues decomposition, [стЕаR + ЩМт ]-2 Hi H X [CTEtr (RAAH R+ CT,IMR )] (45) XHI[CTEaR + ц1мт ] = [V V]^Л 0)[ V V]H The entries of Л are zero. V is the MTx r matrix composed of the eigenvectors corresponding to nonzero eigenvalues. Л values are arranged in nonlinear order without the loss of generality. By putting (39)(40) into (43)(44), ц and a unknowns can be formulated in two equations which can be easily calculated. The updated algorithm based on the previous algorithm which calculated the optimum results with the property of reducing the value of objective function at each iteration, has been shown in Table.2. With increased number of iterations, the algorithm give the A' and B' upto a unitary transform and a unique optimum covariance matrix can be obtained using Q ’ = A'A'H . This optimum covariance matrix reduces to the capacity results as obtained in [9, 44] if the estimated variance has been considered as zero. With the partial CSR knowledge, the optimum transmitters for maximized (17) and minimized (28) share the same structure differing only in power allocation. Finally it is seen that the optimum solution for (28) as A' and B' gives the optimum solution for (17) using Q' = A'A'H which further shows the global maximum for (17) and global minimum for (28). VII. Results and Discussions The broad capacity analysis has been performed by deriving the order statics techniques, reducing the MSE, maximizing the mutual information by implementing the proposed algorithm followed by the improved results in enhancement of overall capacity and reduction in pilot symbols for different combination of MIMO antennas. Figure.4.(a) shows the capacity of the different MIMO antenna combinations and their capacity increase with the increase in transmitting and receiving antenna elements for the condition when CSI is known to transmitter with the spatial heterogeneous behavior. It is clearly apparent from the existing analysis and simulated results that the capacity increases with the increase in transmitter and receiver antenna elements. It is known that with CSI, zero forcing beamforming completely removes the interference between the transmitting antenna in 1+аШ к z h цк ( j e 5, j * к Now this capacity reduces to two different forms depending upon the number of antennas [45] C = E C = Z log2 (1 +Pk\\hk\|2 ) . к e 5 , м Г.Г, ( / II, l|2\)ZE log2{max(PkWhkW)} i=1 [ v keTi x i=1 Table 2: 1) Initialize A 2) Update R^ using (10) with Q = AAH т о • B = XHHH (HXXHHH R )-1 3) Update B using 4) Update ц and a . 5) Update A using A = [ц! + аст^RMt ] HHBH such that tr (AAH) = p (47) is found when channel gain is reduced since zero forcing beamforming reduces to negligible with proper selection of semi orthogonal parameters, i.e. lim |h^H цк| = 1 and (48) is found with ^{^kir}»1 with large number of antennas. Figure.4 and Figure.5 shows that the capacity increases with the increase in number of antennas K. It has been observed that the analysis has been found near to practical propagation scenario on comparing the analytical and simulated results and the difference between then has come out from the loose bound of extreme order statistics for small number of antennas and non-trivial semi orthogonal parameter e . With partial CSI, hk ^ hik, the interference remain in the reception of the signals at the receiver end due to which denominator in (46) exists. Using [46, 47], the capacity reduces to C > M jlog2 (1 - §) + + 1, M log2M -1 PkWhA|2 hH Ц 1+PkWhA Г (sin20k) S Pj j G 5, j * k where, в denotes a distributed random variable with parameter (1, M+N-1). Figure.4(b) shows the probability distribution function(PDF) of sin20 which has been found using cumulative distribution function(CDF) of sin20 and further been derived as Г к RM + N -1)2(M+N-1) xM-2 f sin 0(x) = •! B 0 < x< § x ^ § where, § = 2 M+N-1 Figure,6 shows the capacity for the partial CSI condition for 2x2 and 4x4 antenna configurations. It has been observed that with lower SNR conditions, significant improvement in capacity has been seen with the increase in number of transmitting and receiving elements. Whereas in case when the SNR is high, capacity of MIMO system with spatial channel becomes interference limited and this interference limited capacity increase with the quantization factor B. Figure.5(a) shows that the capacity of the MIMO system with known CSI is better than the capacities with partial CSI or unknown CSI which has been limited due to lower bound conditions. Figure.5(b) shows the comparison of capacity with partial CSI and the new capacity found using adaptive method with partial CSI, which shows improvements at the lower SNR conditions as compared with the capacity with the partial CSI. At higher SNR conditions, this estimation scheme has also the interference limited bound with them but still a good result has been found using this estimation scheme as compared with the existing partial CSI condition, which has been achieved using the following bounds [48], C lim B ^w M * B / M *-1 = 1 i.e. K e S .sin2 0) S Pj j ek, j * k sin2 0k) EI S Pj ^ j e k, j * k -B _ 2 M+N-1 (50) has been found with the fact of growth of p ||h ||2, (51) comes from the Jensen’s inequality and (52) has been formulated for the proposed estimation method for capacity with partial CSI knowledge. Figure.6,7,8 has been shown for different training sequences that has been deployed with the transmitting signal sequence. Here in Figure.6(a), constellation for training sequence in transmitting signal sequence has been shown for the MIMO channel with partial CSI with the correlation coefficient of 0.5 between the transmitting antenna elements, whereas in Figure.6(b), Gold training sequence has been taken in consideration with correlation coefficient of 0.5. The gold sequence is denoted as Zn ={Zn }2n_Q1with length 2" , where , Zn = 0 , Zn = 1 This generation is repeated for m times depending on the number of sub-channels. The resultant modulated signal for mth will be m sm = U Cn = Um exp I j 2n ...) , ■ , , . mn which have a good M 2n J 6 periodic autocorrelation characteristic. It can be seen that the comparison of both Figure.6(a) and (b) shows that the gold sequence constellation is tightly bounded under the exploring region and does not interferes the other signals. In Figure.7(a) and (b), the training sequence with partial CSI channel and proposed estimation based channel has been shown, in which Figure.7(a) significantly shows that the constellation is moving away or reaching at the edges of its exploring boundaries whereas in Figure.7(b), where the proposed scheme has been implemented, can be easily seen exploring inside its region. Similarly Figure.8 (a) and 9(b) has been found for the higher SNR with correlation coefficient of 0.5, in which it can be seen that for the partial CSI channel, the constellation of the training sequence are moving out of the exploring region may not be detectable at the receiver end which leads the system to estimate the transmitted signal incorrectly. Whereas in Figure.8 (b), it can be seen that a few training symbols are diverged but are confined under the exploring boundaries which leads the MIMO system to estimate the data at the receiver end. To make the symbols more confined, number of iterations can be raised which will lead to more accurate symbol confinement. Figure.9(a) and (b) shows the comparison of the received constellation for 16-QAM modulation scheme for both channels i.e. with known CSI knowledge and partial CSI knowledge, in which it can be seen that the symbols in the partial CSI case, are more diverged but still detectable, whereas in Figure.10(a) the 16-QAM constellation has been received at the receiver end for the channel with partial CSI knowledge implemented with the proposed estimation, which shows less divergence of the symbols at the receiver end when the system is simulated with correlation coefficient of 0.5. Similarly, if the higher SNR case is considered, the received constellation is shown in Figure.10(b) which shows the divergence of the received symbols in good quantity. These noise or the incorrect estimated symbols can be rectified by increasing the number of iterations in the channel estimation process. Figure.11(a) and (b) shows the comparison of the capacity of the channel with partial CSI with proposed method, known CSI (waterfilled) and known CSI channel with equal power for two different MIMO antenna configurations of 2x2 and 4x4. The partial CSI capacity optimal power allocation improves from the known CSI capacity at 1.5dB and maintains this upto 16.5dB where both partial CSI capacity and known CSI known capacity with waterfilling starts to decrease as with the equal power capacity of the known CSI capacity. At 20dB, the partial CSI approximates with the known CSI which then again improves after 22dB. This shows that, at higher SNR, the capacity for both partial CSI and known CSI approximates to the lower of the equal power capacity with known CSI. Figure.11(b) has been shown for 4x4 MIMO antenna for all the three said channel capacities comparison as said above. A number of variations have been found at the higher SNR levels for this 4x4 configurations. At lower SNR levels, the partial CSI channel with proposed scheme has the advantages over the known CSI and the capacity with equal power. With the increase in SNR at 18dB, channel capacity with known CSI start to decrease with equal power channel capacity, whereas the partial CSI capacity is still higher than both of the capacities. With some more increase in SNR at 18.8dB, capacity with partial CSI starts decreasing with equal power but remains in between the remaining two capacities. At 22.9dB, the capacity with partial CSI starts to decrease and both capacities i.e. with partial CSI and with known CSI come less than the capacity with equal power. Further at 24.6dB the capacity with known CSI again increases as compared with the capacity with equal power, here capacity with partial CSI still remains less with both of them. At last, the capacity with partial CSI again improves and moves ahead of capacity with equal power at 26.5dB, but at this stage too, capacity with known CSI is higher than the said two capacities i.e., higher by 0.2 dB only. These large variations in the capacities are due to the channel mean and the variance i.e., higher the variance, more variations will result which is due to the difference in the power allocation. Figure.12 shows the mutual information with the eigenvalues of Q for two different antenna configurations i.e. 2x2 and 4x4 with three different scheme comparisons i.e. mutual information with known CSI (waterfilling), partial CSI and known CSI with equal power are shown. A zero mean variance one has been considered for the channel and the results shows that the optimal power for partial CSI follows the path for the known CSI channel in the case of 2x2 MIMO antenna systems in which the Energy level starts to reduce after 15dB and reached the equi-power level near about at 25dB. The same pattern has been found for the case of 4x4 MIMO antenna systems but with large Energy level in between 5dB to 25dB. The mutual information (power allocation) at higher SNR for the partial CSI known channel approaches equi-power channel with known CSI as the channel with known CSI has approached. At some instants, the mutual information deviates to follow the known CSI which occurs due to the occurrence of Jensen’s inequality covariance at those instants. With higher SNR and higher antenna elements, the optimized mutual information may converges to non equi-power channel with known CSI. But after implementing the adaptive estimation based scheme for 4x4 MIMO antenna systems, the channel with partial CSI also approaches equi-power channel as the channel with known CSI does i.e. it follows the same path but with large Energy levels. Fig.4: Capacity analysis for different antenna configuration with known CSI(with waterfilling) and its PDF distribution Capacity in Bits/sec/Hz Fig.5: (a) Comparison of Capacity analysis for 2x2 and 4x4 MIMO antenna with known CSI and unknown CSI (b) Comparison of capacity analysis with unknown CSI for 2x2 and 4x4 MIMO antenna for existing and proposed estimation scheme Fig.6: (a) Training sequence constellation in channel with known CSI with correlation coefficient of 0.5. (b) Constellation in channel with known CSI with correlation coefficient of 0.5 for gold training sequence. Fig.7: Training sequence constellation for partial CSI known channel with proposed estimation for correlation coefficient of 0.1 and 0.5. Fig.8: Training sequence for SNR 35dB with correlation coefficient of 0.5 for channel with partial CSI and proposed estimation scheme Fig.9: Received 16-QAM constellation for the channel with known CSI and partial CSI Fig.10: Received 16-QAM constellation for Partial CSI channel using modified precoder and decoder with correlation coefficient of 0.5. (b) Received 16-QAM constellation for Partial CSI channel using modified precoder and decoder for SNR 35dB and correlation coefficient 0.1. Fig.11: Comparison of Ergodic capacity with proposed partial CSI, known CSI with waterfilling and known capacity with equal power with the correlation coefficient of 0.5 using the modified precoder and decoder. Fig.12: Analysis of the eigenvalues of the transmit covariance matrix for 2x2 and 4x4 MIMO antenna system We have tried to design a new adaptive algorithm which has been implemented with the MIMO capacity lower bounds to maximize the capacity with the lower pilot symbols requirement in the partial CSI knowledge conditions for the spatial channels. Also the increase in mutual information and reduction in Mean square error has been tried with determination of optimum covariance matrix in precoder form for the transmit correlation matrix. The adaptive estimation based optimized precoded MIMO system shows the advantages in capacity enhancement as compared with existing partial CSI conditions and equal power allocation scheme after implementing the proposed adaptive estimation scheme and the modified precoder and decoder at the transmitter and receiver end. Different estimation methods and comparison for transmitted training symbols have been tried and their improved results based on adaptive estimation method have been shown with the consideration of different correlation coefficient values for the transmitting antennas. At last, based on the eigenvectors knowledge of transmit covariance, optimized capacity achieving eigenvalues of the transmit covariance matrix has been shown and found that the gap between the power of eigenvectors for higher antenna configuration has been reduced and it started to follow the equi-power channel mutual information with large energy levels. Acknowledgement The authors thankfully acknowledge the support provided by the authorities of Jaypee University of Engineering and Technology, Guna, India.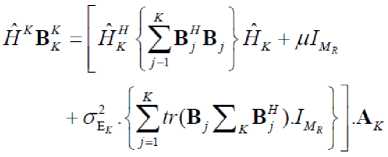
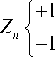
VIII. Conclusion
Список литературы MIMO Capacity Analysis Using Adaptive Semi Blind Channel Estimation with Modified Precoder and Decoder for Time Varying Spatial Channel
- G. J. Foschini, "Layered space-time architecture for wireless communication in a fading environment when using multi-element antennas," Bell Labs Technical Journal, vol. 1, pp. 41-59, 1996.
- I. Barhumi, G. Leus, and M. Moonen, "Optimal training design for MIMO OFDM systems in mobile wireless channels," IEEE Trans. Signal Process., vol. 51, pp. 1615-1624, 2003.
- D. Schafhuber, G. Matz, and F. Hlawatsch, "Adaptive Wiener filters for time-varying channel estimation in wireless OFDM systems," IEEE International Conference on Acoustics, Speech, and Signal Processing, 2003. Proceedings. (ICASSP '03). 2003, 2003, pp. IV-688-91 vol.4.
- R. Kumar and R. Saxena, "Capacity Analysis of MIMO Spatial Channel Model using Novel Adaptive Semi Blind Estimation Scheme," Journal of Wireless Networking and Communications, vol. 2 No.4, 2012.
- M. J. Gans, "A power-spectral theory of propagation in the mobile-radio environment," IEEE Transactions on Vehicular Technology, , vol. 21, pp. 27-38, 1972.
- T.S.Rappaport, Ed., Wireless Communications:Principles & Practice. Saddleriver, NJ: Prentice Hall PTR, 1996.
- P.Zetterberg and B.Ottersten, "The Spectrum Efficiency of a Basestation Antenna Array System for Spatially Selective Transmission," in IEEE VTC, 1994.
- E. Karami and M. Shiva, "Decision-Directed Recursive Least Squares MIMO Channels Tracking," EURASIP Journal of Wireless Commun. Networking, pp. 1-10, 2006.
- E. Telatar, "Capacity of multi-antenna Gaussian channels," Bell Labs Technical Memorandum, June 1995.
- S. N. Diggavi and T. M. Cover, "The worst additive noise under a covariance constraint," IEEE Transactions on Information Theory, x, vol. 47, pp. 3072-3081, 2001.
- S. Boyd, S. Vishwanath, and A. J. Goldsmith, "worst-case capacity of Gaussian Channel Vectors," 2002.
- E. Visotsky and U. Madhow, "Space-time transmit precoding with imperfect feedback," IEEE Transactions on Information Theory, , vol. 47, pp. 2632-2639, 2001.
- A. F. Molisch, M. Steinbauer, M. Toeltsch, E. Bonek, and R. S. Thoma, "Capacity of MIMO systems based on measured wireless channels," IEEE Journal on Selected Areas in Communications, , vol. 20, pp. 561-569, 2002.
- A. Moustakas and S. Simon, "Optimizing multi-transmitter single-receiver (miso) antenna systems with partial channel knowledge."
- S. A. Jafar and A. Goldsmith, "Transmitter optimization and optimality of beamforming for multiple antenna systems," IEEE Transactions on Wireless Communications, , vol. 3, pp. 1165-1175, 2004.
- S. A. Jafar and A. J. Goldsmith, "On optimality of beamforming for multiple antenna systems with imperfect feedback," in Proceedings of Int. Symp. Inf. Theory, June 2001, p. 321.
- S. A. Jafar, V. Sriram, and A. Goldsmith, "Channel capacity and beamforming for multiple transmit and receive antennas with covariance feedback," in IEEE International Conference on Communications, 2001. ICC 2001., 2001, pp. 2266-2270 vol.7.
- E. A. Jorswieck and H. Boche, "Optimal Transmission with Imperfect Channel State Information at the Transmit Antenna Array," Wireless Personal Communications, vol. 27, pp. 33-56, 2003.
- E. A. Jorswieck and H. Boche, "Channel capacity and capacity-range of beamforming in MIMO wireless systems under correlated fading with covariance feedback," IEEE Transactions on Wireless Communications, , vol. 3, pp. 1543-1553, 2004.
- S. Simon and A. Moustakas, "Optimizing MIMO antenna systems with channel covariance feedback."
- G. J. Foschini and M. J. Gans, "On limits of wireless communications in a fading environment when using multiple antennas," Wireless Personal Communications, vol. 6, pp. 311-335, 1998.
- A. Narula, M. J. Lopez, M. D. Trott, and G. W. Wornell, "Efficient use of side information in multiple-antenna data transmission over fading channels," IEEE Journal on Selected Areas in Communications, , vol. 16, pp. 1423-1436, 1998.
- T. L. Marzetta and B. M. Hochwald, "Capacity of a mobile multiple-antenna communication link in Rayleigh flat fading," IEEE Transactions on Information Theory, , vol. 45, pp. 139-157, 1999.
- Z. Lizhong and D. N. C. Tse, "Communication on the Grassmann manifold: a geometric approach to the noncoherent multiple-antenna channel," IEEE Transactions on Information Theory, , vol. 48, pp. 359-383, 2002.
- A. Lapidoth and S. M. Moser, "Capacity bounds via duality with applications to multiple-antenna systems on flat-fading channels," IEEE Transactions on Information Theory, , vol. 49, pp. 2426-2467, 2003.
- T. Cui and C. Tellambura, "Semiblind Channel Estimation and Data Detection for OFDM Systems With Optimal Pilot Design," IEEE Transactions on Communications, , vol. 55, pp. 1053-1062, 2007.
- W. Feng, W. P. Zhu, and M. N. S. Swamy, "A Semiblind Channel Estimation Approach for MIMO OFDM Systems," IEEE Transactions on Signal Processing, , vol. 56, pp. 2821-2834, 2008.
- M. Abuthinien, S. Chen, and L. Hanzo, "Semi-blind Joint Maximum Likelihood Channel Estimation and Data Detection for MIMO Systems," IEEE Signal Processing Letters, vol. 15, pp. 202-205, 2008.
- M. A. Khalighi and S. Bourennane, "Semiblind Single-Carrier MIMO Channel Estimation Using Overlay Pilots," IEEE Transactions on Vehicular Technology, vol. 57, pp. 1951-1956, 2008.
- Y. Jung-Lang and L. Yin-Cheng, "Space-Time-Coded MIMO ZP-OFDM Systems: Semiblind Channel Estimation and Equalization," IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 56, pp. 1360-1372, 2009.
- C. Yi-Sheng, "Semiblind Channel Estimation for MIMO Single Carrier With Frequency-Domain Equalization Systems," IEEE Transactions on Vehicular Technology, vol. 59, pp. 53-62, 2010.
- W. Feng, Z. Wei-Ping, and M. N. S. Swamy, "Semiblind Sparse Channel Estimation for MIMO-OFDM Systems," IEEE Transactions on Vehicular Technology, vol. 60, pp. 2569-2582, 2011.
- K. Kyeong Jin, T. A. Tsiftsis, and R. Schober, "Semiblind Iterative Receiver for Coded MIMO-OFDM Systems," IEEE Transactions on Vehicular Technology, vol. 60, pp. 3156-3168, 2011.
- S. A. Jafar and A. Goldsmith, "Multiple-antenna capacity in correlated Rayleigh fading with channel covariance information," IEEE Transactions on Wireless Communications, vol. 4, pp. 990-997, 2005.
- S. Da-Shan, G. J. Foschini, M. J. Gans, and J. M. Kahn, "Fading correlation and its effect on the capacity of multielement antenna systems," IEEE Transactions on Communications, vol. 48, pp. 502-513, 2000.
- L. Musavian, M. R. Nakhai, M. Dohler, and A. H. Aghvami, "Effect of Channel Uncertainty on the Mutual Information of MIMO Fading Channels," IEEE Transactions on Vehicular Technology, vol. 56, pp. 2798-2806, 2007.
- B. Hassibi and B. M. Hochwald, "How much training is needed in multiple-antenna wireless links?," IEEE Transactions on Information Theory, vol. 49, pp. 951-963, 2003.
- C. B. Papadias, "Unsupervised receiver processing techniques for linear space-time equalization of wideband multiple input / multiple output channels," IEEE Transactions on Signal Processing, vol. 52, pp. 472-482, 2004.
- G. Caire and S. Shamai, "On the capacity of some channels with channel state information," IEEE Transactions on Information Theory, vol. 45, pp. 2007-2019, 1999.
- A.Paulraj, R.Nabar, and D.Gore. (2003). Introduction to space time wireless communications.
- D. Minhua and S. D. Blostein, "MIMO Minimum Total MSE Transceiver Design With Imperfect CSI at Both Ends," IEEE Transactions on Signal Processing, vol. 57, pp. 1141-1150, 2009.
- S. M. Kay. (1993). Fundamentals of Statistical Processing: Estimation Theory. 1.
- D.P.Bertsekas. (1999). Non Linear Programming.
- H. Sampath, P. Stoica, and A. Paulraj, "Generalized linear precoder and decoder design for MIMO channels using the weighted MMSE criterion," IEEE Transactions on Communications, vol. 49, pp. 2198-2206, 2001.
- I. Sohn, J. G. Andrews, and L. Kwang Bok, "MIMO Broadcast Channels with Spatial Heterogeneity," IEEE Transactions on Wireless Communications, vol. 9, pp. 2449-2454, 2010.
- N. Jindal, "MIMO Broadcast Channels With Finite-Rate Feedback," IEEE Transactions on Information Theory, vol. 52, pp. 5045-5060, 2006.
- Y. Taesang, N. Jindal, and A. Goldsmith, "Multi-Antenna Downlink Channels with Limited Feedback and User Selection," IEEE Journal on Selected Areas in Communications, vol. 25, pp. 1478-1491, 2007.
- M. Vu and A. Paulraj, "Capacity optimization for Rician correlated MIMO wireless channels," in Conference Record of the Thirty-Ninth Asilomar Conference on Signals, Systems and Computers, 2005., 2005, pp. 133-138.


