Минимальные абсолютно представляющие системы экспонент в пространствах аналитических функций с заданной граничной гладкостью

Пусть G — ограниченная односвязная область комплексной плоскости C, для которой int G = G. Через A ^ (G) обозначим пространство всех функций, аналитических в G и бесконечно дифференцируемых вплоть до ее границы ∂G.

Весом будем называть произвольную неубывающую выпуклую на [0, го) функцию у, для которой t = o(y(t)) при t ^ го.                               (1)

Семейство всех весов обозначим символом V . Без ограничения общности будем считать, что у(0) = 0 для любого у G V.

Для ϕ из V образуем банахово пространство

A ^ (G) := ff G A ^ (G): k f k ^

=sup sup z e G k e z ₊

I f ^(k) (z)l k! e *^(k)

< ∞

Возьмем произвольную последовательность Ф = {yn}П=1 функций из V, для которой существуют такие Cn > 0, что yn+i(t + 1) + t 6 yn(t) + Cn (t > 0, n G N),

и образуем пространство A ф (G) = P|n =i A ^ n (G), наделенное топологией, задаваемой набором норм ( k • k ^ n ) П=1 . Заметим, что в силу (2) оно является пространством Фреше — Шварца (коротко, (FS)-пространством).

В дальнейшем мы будем рассматривать лишь выпуклые ограниченные области G комплексной плоскости, что естественно при изучении представления функций рядами из экспонент. В [1] (см. также [2]) было доказано, что в тех случаях, когда сопряженное к A ф (G) пространство допускает так называемое экспоненциальное описание, существуют последовательности экспонент, являющиеся абсолютно представляющими системами (АПС) в A ф (G). Поскольку в пространствах такого типа ни одна АПС экспонент не может составлять базиса (см. [3]; в терминологии монографии [4] такие системы называются свободными), то любая АПС экспонент в A ф (G) заведомо переполнена. В связи с этим традиционно ставится вопрос о минимальных в определенном смысле АПС [5–8]. В настоящей работе этот вопрос изучается для пространств функций с заданной граничной гладкостью, задаваемых с помощью весовых последовательностей, порождаемых одной весовой функцией. Именно, пусть ϕ ∈ V и последовательность положительных чисел (р _п ) П=1 такова, что p n f p Е (0, го ]. Для пространства A ф (G), образованного по последовательности Ф = (p n ^(t/p n )) П=1 , будем использовать специальное обозначение A ^p^) (G). Нетрудно видеть, что оно не зависит от выбора последовательности (р _п ) П=1 , лишь бы p n ↑ p.

В первой части работы при дополнительных ограничениях на ϕ приводится более простое по сравнению с известным представление сопряженного с A p^ (G) пространства. Затем из него выводятся новые по форме и более удобные для приложений критерии для АПС экспонент в A ^p^) (G) и дается описание всех мультипликаторов и достаточные условия для делителей полученной реализации сопряженного пространства. На их основании и с помощью общих результатов из [8] во второй части доказывается существование АПС минимального типа в A ^p^) (G) при p <  го . Наконец, в заключительной третьей части работы АПС минимального типа используются для того, чтобы показать, что для пространств аналитических функций с заданной граничной гладкостью, в отличие от пространств всех аналитических функций, невозможны теоремы о предельном переходе по области.

1.    Пространства, порождаемые одним весом, и их сопряженные

Всюду далее предполагаем без ограничения общности, что выпуклая ограниченная область G содержит начало.

Напомним описание сильного сопряженного с A ф (G) пространства из работы [1, следствие 1].

Свяжем с каждым весом у Е V выпуклую функцию ^(r) = ^(r) + r ln ⁺ e , r >  0. Очевидно, что ψ — вес из V . Через ψ ^∗ обозначим функцию, сопряженную с ψ ∈ V по Юнгу — Фенхелю, т. е. ^ * (s) := sup t>g (ts — ^(t)), s >  0. Ясно, что функция ^ * принимает лишь конечные значения. По ψ ^∗ образуем банахово пространство целых функций

E^. (G) := (f Е H(C) : |F|^* = sup |F(A)’ + < го} , l лес exp(HG(A) + ^*(ln+ |A|)) J где Hg(A) = supzeG Re(Az) — опорная функция компакта G. Для весовой последовательности Ф = {^n}^=i рассмотрим образованную по вышеуказанному правилу последовательность Ф* = {^П}]]=i и соответствующее ей пространство целых функций E^* (G) := и^=1 E^n (G), которое наделим топологией индуктивного предела последовательности пространств (E^n(G))n=1. В силу (2) пространство E^* (G) относится к классу (DFS). В [1] установлена справедливость следующей теоремы.

Теорема A. Пусть G — ограниченная выпуклая область комплексной плоскости. Пусть, далее, Ф = (у _п ) П=1 — последовательность функций из V , для которой выполнено (2) , и известно, что p n (t) = O(t ² ) при t ^ го для каждого n Е N . Тогда преобразование Лапласа функционалов T ^ T (А) := T(e ^Xz ) , Л Е C, устанавливает топологический изоморфизм между сильно сопряженным к А ф (О) пространством (Л ф (О')У_ь и пространством Е ф » (G).

Следствие. Пусть G — ограниченная выпуклая область комплексной плоскости, а у Е V такова, что у (t) = O(t2) при t ^ го. Предположим дополнительно, что для любого q > 1 существует Cq > 0 такое, что qϕ

t

q

+ t 6 у (t) + C q

( V t >  0).

Определим последовательность Ф * , состоящую из функций, образованных по правилу

^ n (s) := ^SU P i ts — P _n y f—) - t ln ⁺ г , n Е N. t> 0 I           pnn^         e J

Тогда преобразование Лапласа функционалов устанавливает топологич ₀ еский изоморфизм между сильно сопряженным к A^ (G) пространством (A p^ (G)) и Е ф » (G) при любом p Е (0, го ] .

<1 В соответствии с теоремой А нам достаточно проверить, что весовая последовательность p _n y(t/p _n ) удовлетворяет условию (2).

Из выпуклости у и того, что у(!) = O(t ² ) при t ^ го , для произвольного фиксированного r > 0 имеем

( (t 'И (tW   A ^{(2 t/r ) -} y ^{( t/r )}    y ^{(2 t/r )}

At

6 — r

44“/ у w)6 t/r 6

при всех t > 1, где постоянная A зависит только лишь от у. Поэтому найдется такое B = B (r) > 0, что у ft) > у^1^) - N • t - B (Vt > 0),                 (4)

rrr где N : = [A/r] + 1.

Далее, положив r := p n+i и применив N + 1 раз условие (3) при q = N+1 p n+l > 1, p n получим

ϕ

t pn

> q ^{N +1} y

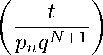
+ (N±^ - D = P n+1 • y(A_ ) + ^{( N} + 1)t - d, p n            p n       p n+i        p n

где D — некоторая положительная постоянная, зависящая лишь от n. Поэтому из неравенства (4), примененного к r = pn+i, следует у (_L) > pn+1. (у (t+1) - nA_ - B) + (N±2)t - D pn      pn        pn+i      pn+i            pn

• > p n+1 . у ( 1+1 ) + L - Bp n+ - D. p n       p n+i     p n      p n

Таким образом, при C n := Bp n+i + Dp n имеем

Pn+1y(--±-)+ t 6 pnP ( — )+ Cn, t > 0, pn+i              pn что доказывает следствие. B

Заметим, что при p = го вместо (3) можно было потребовать выполнения более мягкого условия

( 3 q> 1) ( 3 C> 0) qy(^ + t 6 y(t) + C ( V t >  0).

Обозначим через W — подкласс тех весов ϕ ∈ V , для которых преобразование Лапласа функционалов устанавливает топологический изоморфизм между сильно сопряженным к A ^p^) (G) пространством (A ^p^) (G)) _b и пространством E ^ * (G), где Ф * образована по правилу, указанному в следствии, для любой ограниченной выпуклой области G.

Наша ближайшая цель — выделить подкласс тех ϕ ∈ W , для которых сопряженное можно описать в более простой форме, чем в следствии. В связи с этим рассмотрим те веса ϕ, для которых

y ^{( t )} - qy^t/q)

lim ----— ---- = + го ( V q> 1).                     (5)

t^^      t ln t

Примерами весов, удовлетворяющих (5), являются

• 1)    t ^a , a >  1;

• 2)    t ln ^e (1 + t), в > 2;

• 3)    t(lnt) ^lnlnt .

Ясно, что условие (5) влечет выполнение (3). Далее, из (5), очевидно, следует, что t ln t = o(y(t)) при t ^ го.                               (6)

Установим некоторые свойства весов, удовлетворяющие условию (5) или (6), и ассоциированных с ними весовых последовательностей.

Лемма 1. Пусть вес у удовлетворяет условию (6). Тогда ln у* (s) = o(s) при s ^ го и существует такая постоянная A > 0, что у*(ln+(s + 1)) — у*(1п+ s) 6 A, s > 0.                         (7)

<1 В силу условия (6) на вес у для любого C >  1 найдется такая постоянная D =

D(y, C ) > 0, что при всех t >  0

y(t) >  Ct ln ⁺ t — D.

Поэтому для любого s >  0

У * (s)

= sup(ts — y(t)) 6 sup(ts — Ct ln ⁺ t) + D 6 max

t>0

t>0

{ s, sup(ts — Ct ln t) I + D.

I t>i                  >

Так как

C es/C sup(ts — Ct ln t) = < e t>i                      s

при s > C, при 0 6 s < C,

и Ce ^s/C

> s при любом s >  0, то окончательно имеем, что y * (s) 6 se^ s/C + D ( V s >  0).

Отсюда в силу произвольности C >  1 получаем, что ln у * (s) = o(s) при s ^ го , и тем более y * (s) = o(e ^s ) при s ^ го .

Таким образом, для ϕ ^∗ выполнены все условия леммы 6.1.2 из [9], в соответствии с которой у * удовлетворяет (7). B

Лемма 2. Пусть вес у удовлетворяет условию (5) , p n f p Е (0, го ] , ^ n (t) := p n y(t/p n ) + t ln ⁺ (t/e) (n Е N) . Тогда весовые последовательности Ф * := (^ n (s)) n=1 и Ф * := (pny* (s)) n=i удовлетворяют при некоторых постоянных C _n > 0 неравенствам

^ n (s) 6 P n ^ * (s) 6 C+i (s) + C n , S >  0, n Е N.

• <1 Левая часть неравенства следует без каких-либо ограничений из определения функций ψ _n ^∗ :

С(s) 6 P n sup((t/p n )s — ^(t/p n )) = P n ^ * (s).

t>0

С другой стороны, из условия (5) имеем, что для произвольных q > 1 и A > 0 найдется постоянная C(q, A) > 0 такая, что y(t) > qy(t/q) + tln+(At) — C(q, A) (Vt > 0).

Поэтому для q = p n+i /p n > 1 и A = p _n /e> 0 найдется такая постоянная C _n > 0, что

P n ^ * (s) = p nit up (tS — y(t)) = 8 > p (tS — p n ^(t/p n ))

6 sup ( ts — p n ( qy(t/(qp n )) + (t/p n )ln ⁺ (At/p n ) — C (q, A) )) tU0

= sup ( ts — ( p n+i ^(t/p n+i ) + t ln ⁺ (t/e) )) + C n = C+i (s) + C n (s >  0, n Е N). ▻ tU0

Отметим еще один полезный факт, вытекающий из более слабого, чем (5), условия.

Лемма 3. Пусть вес ϕ удовлетворяет условию lim ''     ’'        +го   (V q> 1).

t→∞

Тогда для любого q > 1 существует Cq > 0 такое, что y* (s + 1) 6 q^* (s) + Cq (V s > 0).(8)

• < По условию для любого q> 1 найдется постоянная C q > 0 такая, что

• qy* (s) = sup (ts — qy ( -    > sup (t(s + 1) — y(t)) — Cq = y* (s + 1) — Cq.

t>0 V         kq/ /

Для веса y и последовательности p _n f p Е (0, го ] определим весовую последовательность Ф * := (p _n y * (t)) n=i , а по ней весовое пространство целых функций Е ф * (G), представляющее собой внутренний индуктивный предел последовательности банаховых пространств

E p n _V * (G) := (f Е H (C) : | FU* = sup            | F ^{( Л ) |}    ₊     <  го} .

(                         д_е с exp(H G (A) + p n y * (ln ⁺ | А | ))      J

Будем использовать для этого пространства специальное обозначение Е ^p^ , ) (G). Ясно, что это пространство не зависит от выбора последовательности (p _n ) n=i , лишь бы p _n f p.

Обозначим через W семейство всех весов из W , для которых имеет место условие (5). Из леммы 2 и следствия из теоремы А получаем такой результат

Теорема 1. Для веса ϕ ∈ W преобразование Лапласа функционалов устанавливает топологический изоморфизм между пространством (A p,) (G)) b , сильно сопряженным к A p, (G) , и E( , * ) (G') Для любой ограниченной выпуклой области G и любого p Е (0, го ] .

C Действительно, в силу леммы 2 для каждого n ∈ N справедливы вложения

E(G) ^ E(G) ^ E    (G), n Е N, где vn те же, что и в лемме 2. Отсюда следует топологическое равенство Ep,*) (G) = E^* (G). Остается применить следствие из теоремы A, чтобы получить нужное. B

В дальнейшем нам потребуется описание всех мультипликаторов пространства E ^p, * ) (G), которое мы сейчас приведем. Напомним, что целая функция ц называется мультипликатором множества E целых функций, если ц • E С E. Так как E ^p, * ) (G) является (DFS)-пространством, то всякий его мультипликатор ц непрерывен, т. е. соответствующий оператор умножения Л ^ : f ^ цf действует из E ^p, * ) (G) в E ^p, * ) (G) непрерывно (см. по этому поводу [10]). Это обстоятельство позволяет нам воспользоваться общими результатами из [11] об описании непрерывных мультипликаторов и установить следующий результат, имеющий самостоятельное значение.

Предложение 1. Пусть вес р удовлетворяет условию (5) . Класс M p, * ) (G) всех мультипликаторов пространства E ^p, * ) (G) допускает следующее описание

M ^p, * ₎ (G) = | ц Е H (C) : V е> 0 3 С _е > 0 : | ц(А) | 6 C _e e ^e, * ^{(ln + | A | )} , А Е с } при 0 < p <  го ;

M (, * ) (G) = | ц Е H (C) : 3 C >  0 : | ц(А) | 6 Ce ^C, * ^{(ln + | A | )} , А Е с } .

C Положим hn(A) = exp (Hg(A) + pn^*(ln+ |А|)) (А Е C, n Е N).

Так как у * не убывает и выпукла на [0, го ), то y * (ln ⁺ | А | ), а следовательно, и H g (А) + p n ^ * (ln ⁺ | А |) — субгармоническая в C функция. Далее, для каждого n Е N и любого λ ∈ C

(1 + | А | ² ) ³ sup h n (0 6 exp sup Hg« ) + P n sup y * (ln ⁺ | ^ | )+3ln(1 + | А | ² ) k- a | 6 i               U-A | 6i               i e - A | 6i

6 exp ^Hg(A) + Ag + Рпф*(ln(|A| + 1)) + 6ln+ |A| + 3ln2^, где Ag = supzGG |z| — радиус наименьшего круга с центром в начале, содержащего G. Применив лемму 1 и использовав то, что s = o(y*(s)) при s ^ го, получим, что

Pn^*(ln+(|A| + 1)) + 6ln+ |А| 6 Pn+iy*(ln+ |А|) + An (А Е C), где An > 0 — некоторые постоянные. Тогда для n Е N и А Е с

( 1 + | А | ² ) ³ sup hn(0 6 B n e H G ^{(A)+P n +1} ^(^ ^{| A | )} = B n h n+1 (А), | € - A | 61

где B n : = 8exp(A G + A n ). Таким образом, для весовой системы { h n (A) } n=i выполнены все условия предложения 5 из работы [11], в соответствии с которым E pp * ) (G) является так называемым густым пространством. А тогда по предложению 3 из той же работы Mp’*) (G) совпадает с семейством тех целых функций р, которые удовлетворяют для всех λ ∈ C условию

( V n Е N) ( 3 m Е N) (C n > 0) | ^(А) | 6 C n \ / 6 C n е ^{(Р т - Р п )}’ * ^{(ln + | Л | )} .

h _n ( А )

Отсюда, очевидно, следует описание пространств мультипликаторов в обоих случаях — p Е (0, го ) и p = го . B

Из предложения 1 следует, что класс M p, * ) (G) мультипликаторов не зависит от области и одинаков для всех конечных p. Поэтому в дальнейшем, если не возникнет недоразумений, мы будем применять сокращенные обозначения М (, * ) := M ^p, * ) (G), 0 < p <  го , и M~ := M ~ .(G).

⁽, * )         ⁽₽ • )'

Нетривиальный мультипликатор µ множества E целых функций называется делителем E, если справедлива импликация (теорема деления):

( f Е E, ^f Е H (C) )   = ^ ^f Е E.

µµ

Приведем достаточные условия того, что p Е M (, * ) является делителем E p, * ) (G), где 0 < p <  го .

Предложение 2. Пусть вес ^ удовлетворяет (4) и функция р : (0, го) ^ (0, го) такова, что p(t) = o(^*(lnt)), t ^ го.                                  (9)

Предположим, что для мультипликатора p Е M (, * ) имеет место условие (A) :

( V е > 0) ( 3 R _e >  1)( V А Е C, | А | > R _e )( 3 Z Е C) | Z - А | < р( | А | ), | p(Z) | >  e ^{- ep} * ^{(ln + | z | )} .

Тогда p является делителем пространства E pp * ) (G) для любого p Е (0, го ) и любой выпуклой ограниченной области G.

C Пусть f Е Ep,*)(G) такова, что f/p Е H(C). Из принадлежности f пространству Ep,*)(G) имеем, что при некоторых постоянных q Е (0,p) и Ci ln |f «)| 6 Hg(^)+ q^*(ln+ |e|)+ Ci, e Е C.                   (10)

Возьмем е Е (0,1) так, чтобы q + 6е < p. Так как p Е M(,*), то найдется C2 > 0 такое, что in|p(e)| 6 е^*(in+ |e|) + C2, e е c.                           (11)

Из (7) следует, что y*(ln+(t + 4p(t))) 6 y*(ln+ t) + 4A(p(t) + 1), t > 0.

Кроме того,

Hg(0 6 H g (A)+4A g p( | A | ), | e - A | 6 4р( | А | ); A,e Е C.

Тогда, применив в последних двух неравенствах условие (9), получим, что имеется такое R >  1, что

• y * (ln(t + 4p(t))) 6 (1 + s _i )y * (Int), t >  R, E _i := min(s, s/q);            (12)

Hg«) 6 H g (A) + sy * (In | A | ), | e - A | 6 4p( | A | ), | A | >  R.               (13)

Из условия (А) найдем соответствующее Re. Без ограничения общности можно считать, что Re > R. Рассмотрим произвольное A G C с |A| > Re. Учитывая неравенства (10)–(13), имеем lnmaxmn |f(^6 hg(a)+Ey*(ln |A|) + q(1+Ei)y*(ln |A|)+Ci |$-A|64p(|A|)

6 H G (A) + (q + 2s)y * (ln | A | ) + C i ;

ln max     | д(£) | 6 e(1 + E i ) y * (ln | A | ) + C 2 6 2sy * (ln | A | ) + C 2 .

| § - A | 64p( | A | )

С другой стороны, из оценки НС) | снизу, фигурирующей в условии (А), и (12) получаем

Ь max НО >  ln ^|^ ^(z ) | >  - ^E^* ^{(ln | z} | ) >  ^{- e(1} + ^E i )y * ^{(ln | A | )} >  ^-2e^* ^{(ln | A | )} . ^| § ^- A ^| 6p^{( |} A ^{| )}

Как известно (см. [12]), ln

f (A) O^{A )}

6 ln max    | f (£) | + ln max

| § - A | 64p( | A | )                     | § - A | 64p( | A | )

HO^{- 2ln}_lt maH,J^(O- ^| § ^- A ^| 6p^{( |} A ^{| )}

Использовав в этом неравенстве полученные выше оценки, приходим к следующему неравенству, справедливому при всех |A| > Re, ln

f (A) ^ ^{( A )}

^{6 H} G ^{( A ) + ( q + 6e)} y * ^{(ln | A | )} + C i + C 2 .

Так как в соответствии с выбором E у нас q + 6e < p, то отсюда следует, что f/^ при надлежит пространству Epp* )(G). B

2. Минимальные АПС экспонент в App)(G). Общие результаты

Всюду ниже, если не оговорено дополнительно, p G (0, го ) и у — вес из W.

Как уже отмечалось во введении, АПС экспонент в пространстве A pp) (G) заведомо переполнены. В таких случаях возникает задача о построении минимальных в определенном смысле АПС экспонент. Мы будем исходить из общего понятия минимальности АПС, введенного в [8] на основании классических результатов А. Ф. Леонтьева о представлении аналитических в выпуклой области комплексной плоскости функций рядами Дирихле, показатели которых являются нулями целых функций минимально возможного роста. План изложения в текущем параграфе заключается в конкретизации и проверке основных определений и результатов из [8] для систем экспонент и пространств A pp) (G) и E pp , ) (G). Для удобства читателя мы согласуем некоторые наши обозначения с [8] и при необходимости приведем нужные нам понятия из этой работы.

Положим H := A p^) (G), e(A) := exp Az (A G C) и E := E p^ * ) (G). Для краткости будем использовать обозначение || • ||q := || • ||_qpk /q) , q G (0, го ). В рассматриваемом случае справедливо следующее уточнение леммы 1 из [1].

Лемма 4. Пусть вес у G V удовлетворяет условию (5). Тогда для любых 0 < r < q < го существует такая постоянная c = c(q, r) > 0, что ceHGW+r^*(ln+ H) ^ |e(A)|q 6 eHG(A)+q^(ln+ |A|), A G C.               (14)

<1 Правая часть (14) верна без каких-либо ограничений на у:

| e ^λz |·| λ | ^k

|e(A)|q = SUP sup -----—— zeGkez+ k!eq^ q)

k

6 exp H g (A) + sup I k ln ⁺ | A | — In k! — qy I — L          k e z + V                      Vq

6 exp

H g (A) + sup t>0

t ln ⁺ | A |

-

t qϕ

q

= exp [Hg(A) + qy * (ln ⁺ | A |>]    ( V A G C).

Докажем теперь левую часть (14). При | A | 6 1 имеем

| e(A) | q >  sup | e ^Az | = e ^H G ^(A) .

z ∈ G

Пусть теперь | A | > 1. Тогда

|e(A)|q = sup sup zeGkez+

| e ^λz | · | λ | ^k

k!ew

= exp

k

H g (A) + sup I k In | A | — In k! — qy I — k e z + V                    \q

> exp

H G (A) + sup k e z +

k ln | A |

— k ln ⁺ k — qy

Возьмем E o > 0 так, что r + E o < q. Из условия (5) следует, что при некотором B >  0

(r + E o ) у ^—+— J >  qy     + t ln ⁺ t — B, t >  0.

Продолжив оценку | e(A) | _q , получим отсюда

^{| e ( A ) |} q >  exp

Hg(A) + sup k ln |A| — (r + Eo)y —•---   — B k€Z+\                  Vr + Eo//

> exp

H g (A) + sup (t ln | A | — (r + E o )y ( t>o

—— ) ) — ln | A | — B r + Eo))

= exp [Hg(A) + (r + E o )y * (ln | A | ) — ln | A | — B].

Учитывая еще, что x = o(y * (x)) при x ^ + го , заключаем, что при некотором C > B , не зависящем от λ,

||e(A) | q >  exp [ H g (A) + ry * (ln | A | ) — C ] .

Объединив эту оценку с (15) и положив c := e ^{- C} , получаем левую часть (14). B

Из леммы 4 следует, что для любого p G (0, го) и pn f p весовые системы (exp(HG(A) + pny*(ln+ |A|)))n=1 и (|e(A)|pn)П=1 эквивалентны в том смысле, что для каждого n G N и любого λ ∈ C при некоторых положительных постоянных cn и Cn г Р HG(A)+Pn ^*(ln+ |A|) cn e

6 IHA)!^

6 C n e H G ^(A)+P n +1 ^ * ^{(ln + | A | )}

Отсюда следует, что во всех определениях, результатах, оценках и т. п. из работы [8], касающихся пространств A p_p) (G) и E p_p » ) (G), мы можем использовать exp(H G (A) + P n ^ * (ln ^{+ |A| ))} вместо ||e ⁽ A ^{) k} p n .

Отметим следующие три момента:

• 1)    Экспоненты e(A) являются собственными функциями оператора дифференцирования D : f ^ f 0 , причем совокупность всех решений уравнения Df = Af образует в H одномерное подпространство, натянутое на элемент e(A). Заметим также, что оператор дифференцирования действует непрерывно из H в H (см. [3, лемма 1]).

• 2)    Так как по предположению вес ϕ входит в класс W , то преобразование Лапласа F : v ^ z>(A) = v(e(A)) устанавливает топологический изоморфизм между H 0 и пространством E , которое в силу (16) совпадает с ind E _n , где

E n := gg £ H (C) : | g | n := sup ^(^ <  го) (n G N).

I                             л е с ll^{e ( A )} k P n         J

• 3)    Из условия (7) имеем, что

• sup(Hg(A + £) + pn^*(ln+ |A + £|)) 6 Hg(A) + pn^*(ln+ |A|) + A + Ag,     (17)

I € I 61

где, как и прежде, A g = sup {| z | : z G G } . Отсюда, как известно, следует, что пространство E инвариантно относительно деления на полиномы. Впрочем, тот же самый вывод можно, очевидно, сделать с помощью предложения 2.

Таким образом, для пространств H = A p_p) (G) и E = E ^p^ , ) (G) и системы экспонент E := { e(A) := exp Az, A G C } выполнены все предварительные условия работы [8].

Пусть Л = (A k ) ^ 1 — последовательность попарно различных комплексных чисел с единственной предельной точкой на бесконечности и E (Л) := (exp A k z) ^ 1 — соответствующая ей система экспонент. Из леммы 4 следует, что в рассматриваемом нами случае общее понятие минимальной системы элементов, введенное в [8], интерпретируется следующим образом.

Система E (Л) называется минимальной для A ^p^) (G), если существует такая нетривиальная целая функция L, которая удовлетворяет следующим условиям:

• (a)    ( V e> 0)( 3 R _e >  1) ln | L(A) | 6 H g (A) + (p + e) y * (In | A | ), | A | >  Ry

• (b)    L имеет в точках A k простые нули (она может иметь нули произвольной кратности в других точках).

Совокупность всех функций L, удовлетворяющих условиям (a) и (b), обозначим символом L P (G;Л).

Для дальнейшего изложения нам потребуется следующий вспомогательный результат, касающийся, так называемых, правильных пар. Определение таких пар технически громоздко и само по себе в данной статье не используется. Поэтому мы его приводить не будем, отослав читателя за подробностями к работе [8].

Лемма 5. Пусть вес y G V удовлетворяет условию (5) и E (Л) — минимальная для A ^p^) (G) система. Тогда пара (E (Л),А ^р^) (G)) является правильной.

• <1    Положим k n (A) := exp (Hg(A) + p n y * (ln ⁺ | A | )), A G C, n G N, и отметим, что условие (14) означает, что весовые системы ( | e(A) k p _n : n G N) и (k n (A) : n G N) эквивалентны между собой. Значит, мы можем использовать в наших рассуждениях одну вместо другой. Положим еще k _n,_m (A) := k m (A)/k _n (A), m > n, n G N, A G C.

В соответствии с [8, с. 492–493] (см. пп. а), б)) для доказательства правильности пары (E (Л), A p^) (G)) достаточно проверить следующие условия:

• (i)    функции из L p (G) имеют конечный порядок;

• ^{(ii)    ( V} n ^{)( 3} m ⁾⁽ 3 C> 0) sup | _€ | 6! ||e ⁽ A + ^) k _P n ⁶ C||e ⁽ A ^{) k} p m , A G C;

• (iii)    функции k n,_m (A) радиальны, а In k n,_m (A) субгармоничны в C (m > n, n G N);

• (iv)    ( V n) ( V s > n) ( 3 m > n) ( 3 a > 1) k n,_s (aA) 6 Ak n,_m (A), A G C.

• (i)    Из условия (a), участвующего в определении класса L^p * (G), и того, что lny(s) = o(s) при s ^ го (см. лемму 1), следует, что элементы из L^p * (G) являются целыми функциями порядка не выше первого (более того, если их порядок равен 1, то они имеют конечный тип и индикатор, не превосходящий H G (e i )).

• (ii)    Перепишем (17) в виде

sup k _n (A + £) 6 e ^A+A G k n (A), A G C, n G N.

I € I 61

Отсюда, в силу отмеченной выше эквивалентности весовых систем ( | e(A) | _p n : n G N) и (k _n (A) : n G N), получаем справедливость (ii).

• (iii)    Имеем k _n,_m (A) = e (^{P m - p} n ^)p * ^{(ln + | А | )} , A G C, откуда следует, что функции k _n,_m (A) радиальны в C. Далее, так как у * не убывает и выпукла на [0, го ), то функции ln k _n,_m (A) = (p m — p n )y * (ln ⁺ | A | ) субгармоничны в C при всех m> n.

• (iv)    Возьмем произвольные n,s G N, s > n. Положим m := s + 1, a := e. Тогда в силу (8) для q := ^Рр ⁺ --^{Р п} > 1 имеется A >  0 такое, что при всех A G C

k _ns (aA) = _e ⁽P = ^- P n ^)p * ^{(ln + e | A | )} 6 _e ⁽P s - P n ^{)p , (ln +} W+i) 6 e ⁽P s +i - P n ⁾^ * ^{(ln +} | A ^{| )}+A = _e ^A k n m (A).

Таким образом, выполнены все требуемые условия (i)–(iv), что обеспечивает правильность пары ( E (Л), A ^p^) (G)). B

Теорема 2. Пусть p G (0, го ) , у — вес из W, E (Л) — минимальная для A ^p_p) (G) система и L G L ^p * (G;Л) . Для того чтобы E (Л) была АПС в A ^p^) (G) , необходимо, чтобы для некоторого нетривиального мультипликатора µ из M ϕ ∗ выполнялись условия:

A)

B)

3 Г п t + го :

^ ^{( A )} L(A)

6 e - ^H G ^{(A) - p} n ^p * ^(ln | А | ) ,    | A | = r n , n G N;

r            1

lim sup —-,    T- k x y*(ln |Ak |)

ln

y(A k )

L 0 (A k )

+ H G (A k )

6 - p.

Эти же условия достаточны для того, чтобы E (Л) была АПС в A ^p^) (G) , если они выполняются для некоторого делителя пространства E ^p^ , ) (G) .

С Из того, что класс L p (G; Л) состоит из функций экспоненциального типа и леммы 5 следует, что выполнены все условия теоремы 3 работы [8]. Поэтому достаточно проверить эквивалентность приведенных условий A) и B) с соответствующими им из [8]. Напомним их, отметив как условия A 0 ) и B 0 ), так как символы A) и B) уже используются:

A 0 )

B ⁰ )

3 Г п t + го :

y(A)         1

L(A) 6 k e(A) | p n

| A | = Г п , n G N;

X j LP k j| k e(A k ) k p n <  го ( V n G N).

Эквивалентность условий A) и A 0 ) получаем непосредственно из леммы 4.

Далее, предположим, что для некоторого нетривиального мультипликатора µ из Mϕ∗ ряд Pk=i ILTXkJi l|e(Ak)kpn сходится при каждом n E N. Отсюда следует, что последовательность общих членов ряда ограничена (при каждом n). Учитывая (14), получаем, что тогда для каждого n E N найдется такая постоянная Cn > 0, что у*(ln A|)

ln

^(A k ) L(A k )

⁺ H G ^(A k ) 6 - p n ⁺

C n у * (In | A k | )

( V k E N).

Переходя здесь сначала к верхнему пределу по k, а затем к пределу по n, получаем B).

Таким образом, B 0 ) ^ B).

Пусть теперь имеет место условие B). Тогда для каждого n E N при некоторой положительной постоянной C = C(n) выполняется неравенство

( V k E N).

exp[H G (A k ) + P n+i y * (ln | A k | )] 6 C ^{| L(A} k ) |

Учитывая (16) и то, что x = o(y * (x)) при x ^ + го , получим

MA-) k p n 6 A ( ^{V k} E N).

I L (A k ) |                    | A k | 2

где постоянная A > 0 не зависит от k. Поскольку L является целой функцией экспоненциального типа, то, учитывая связь между порядком целой функции и показателем сходимости последовательности ее нулей, заключаем, что ^2^ =1 1/ | A k | ² <  го , откуда получаем B 0 ). B

Так как y(A) = 1 является делителем пространства E pp * ) (G), то из теоремы 2 получаем такой результат.

Следствие 1. Пусть p E (0, го ) , у — вес из W, E (Л) — минимальная для A p^ ) (G) система и L E L p (G; Л) . Если выполнены условия

• (I)    ( 3 r n t + го ) ln | L(A) | >  H g (A) + P n y * (ln | A | ), | A | = r n , n E N;

limi.      ^{ln jL} 0 ^(Xk)I-H G ^(Xk ) — „

• ^{(II)    llm} k ^^     ^ « (in j A k j )      = p _

то система E (Л) является АПС в A^ (G) .

Перейдем к рассмотрению вопроса о существовании функции L, удовлетворяющей всем условиям следствия 1. Исследование основывается на работе [13], в которой получены общие результаты о приближении субгармонических функций, и [14], в которой приводится схема, использованная нами при доказательстве следующей теоремы.

Теорема 3. Пусть p E (0, го ) и вес у E V удовлетворяет условию (6) . Положим u(A) := H G (A)+py * (ln ⁺ | A | ) , A E C . Тогда существует целая функция экспоненциального типа L , обладающая свойствами:

• 1)    все нули Л := (A k ) k =i функции L(A) простые;

• 2)    L(A) E L p (G;Л);

• 3)    для L(A) выполняются условия (I) и (II) следствия 1 .

C Обозначим D(^,r) := { A E C : | A — £ | 6 r } , £ E C, r >  0. По теореме 4 из [13]

для субгармонической в C функции u(A) найдется целая функция L(A), все нули (A k ) k =i которой простые и при некотором 6 >  0 круги D k := D(A k ,5) попарно не пересекаются, причем вне множества E = Ufc =i D k выполняется асимптотическое соотношение

| u(A) — ln | L(A) | | = O(ln | A | ), | A | ^ го .                            (18)

Отсюда, с учетом условия (1), следует, что L(A) E L¹^ * (G;Л).

Положим Dk := Dk, если к 6 1/V^, и Dk := D(Ak, 1/к2) — в противном случае. Тогда круги Dk попарно не пересекаются и при этом имееют конечную сумму радиусов. Учитывая (18) и (1), получаем, что для каждого е G (0,р) при достаточно больших к на границе круга ∂Dk имеет место оценка ln

L(A) λ - λ _k

> Hg ( A ) + (р - е) y * (ln ⁺ | А | ) - ln 6.

Далее, функция ln

L(A) λ - λ _k

гармонична в некоторой окрестности круга D k (к G N). По-

этому из принципа гармонической мажоранты следует, что всюду на D _k \ D _k выполняется

ln | L(A) | >  H g (A) + (р — е) у * (ln ⁺ | А | ) — 2ln к — ln 6.

Так как L(A) — функция экспоненциального типа, то limsup k _? ^ |jj <  го . Тогда для достаточно больших k имеем

к 6 C | A k | 6 (C + 1) | А | ( V A G D k ),

где постоянная C не зависит от к. Учитывая все вышесказанное и то, что t = o(y(t)) при t ^ го, заключаем, что для любого е > 0 при всех достаточно больших к имеет место оценка на Dk \Dk ln |L(A)| > Hg(A) + (р — 2е) у*(ln+ |А|).

Тогда из последнего неравенства и соотношения (19), учитывая, что круги D k имеют конечную сумму радиусов, получаем (I).

Для доказательства выполнения (II) снова воспользуемся гармоничностью функции ln I x — x k I в некоторой окрестности круга D k . С учетом этого свойства из (7) и (19) имеем для достаточно больших k

ln \L' (A k ) | >  min ln λ ∈ ∂D k

L(A) λ - λ _k

> min ( H g (A) + (р — е)у* (ln ⁺ | A | ) ) — ln 6 λ ∈ ∂D k

> H G (A k ) + (р — Е)у * (ln ⁺ | A k | )

- A,

где A — некоторая постоянная, зависящая только от δ,

ε и G. Таким образом,

_г „ ln | L ⁰ (A k ) |— H G (A k )

lim inf------—— --- k^^       y * (ln | A k | )

> р.

Аналогично с помощью (18) показывается, что

_r       ln | L 0 (A k ) |— H G (A k )

lim sup-------—------- k^^         У * (ln | A k | )

6 р.

Откуда и следует нужное. B

Объединяя следствие 1 и получаем

Следствие 2. Пусть p ∈

теорему 3 и используя определение минимальной системы,

существует минимальная АПС экспонент.

(0, го ) , у — вес из W. Тогда в пространстве A p^) (G) всегда

3.    Неустойчивость АПС экспонент в Ap^ (G) относительно предельного перехода по области

Для систем экспонент в пространствах H(G) всех функций, аналитических в выпуклой ограниченной области комплексной плоскости, известен следующий результат, принадлежащий А. В. Абанину (см. [6, гл. 2, § 3, теорема 9]).

Пусть (G n ) n=i — произвольная последовательность выпуклых областей, исчерпывающая G изнутри, т. е. G n С G n+i (n >  1) и |Jn =i G n = G- Тогда всякая система экспонент, являющаяся АПС в H(G n ) при всех n >  1 , будет АПС и в H(G) .

Результаты подобного характера называют теоремами об устойчивости АПС относительно предельного перехода по области.

В [3] нами было установлено, что для пространств вида А ф (G) имеют место теоремы об устойчивости АПС экспонент относительно предельного перехода по весовым последовательностям при фиксированной области, и высказано предположение, что АПС экспонент в этих пространствах не обладают устойчивостью относительно предельного перехода по области. В текущем параграфе с помощью теоремы 2 и ее следствия доказывается справедливость этого предположения.

Нам потребуются следующие известные свойства целой функции g o (А) := sin nA (см., например, [15, с. 51–52]):

• 1)    go — целая функция экспоненциального типа с простыми нулями в точках А = k, причем | g 0 (k) | = п (k G Z);

• 2)    ln | g o (A) | 6 п | А || sin(arg A) | , A G C;

• 3)    для любого 6 G (0,1/2) имеется такая постоянная C g > 0, что

• ln |g0 (A) | > п| A|| sin(arg А) | — Cg, AG [ {A G C : |A — k| < 6}.

В качестве G возьмем квадрат П : = { z : | Im z | 6 п, | Re z | 6 п } . Рассмотрим функцию L(A) := sin nA • sin inA. Из свойств g o следует, что выполнены следующие условия:

• (a)    L — целая функция экспоненциального типа с простыми нулями в точках k и ik (k G Z, k = 0; A = 0 является нулем L второй кратности) и индикатором H n (A) = п( | Im A | + | Re A | ), причем In | L(A) | 6 H n (A), A G C;

• (b)    Пусть 6 G (0,1/2) и U z,g := { A G C : | A — Z | <6 } (Z G C). Имеет место асимптотическое равенство

In | L(A) | = H n (A) + O(1) при A ^ ro , A G [ ( U k,g U U^g k ∈ Z

В частности, это асимптотическое равенство имеет место на системе концентрических окружностей | A | = k + 1/2 (k G N);

• (c)    ln | L 0 (k) | = H n (k) + O(1) = n | k | + O(1) при | k | ^ ro .

Из свойств функции L следует, что множество ее простых нулей Л := { k, ik : k G Z, k = 0 } образует последовательность показателей минимальной для A p^) (П) системы E (Л) при любых фиксированных p G (0, го ) и у из W. В то же время, по теореме 2 E (Л) не может быть АПС в A ^p^) (П) ни при каких p G (0, го ) и у из W, поскольку условие А) этой теоремы не может быть выполнено ни для одного нетривиального мультипликатора µ из М ^ * . В самом деле, если найдется последовательность радиусов r n f + го такая, что

^ ^{( A )} L(A)

6 exp [ — Hn(A) — pn^*(ln |A|)j, |A| = rn n G N, то отсюда немедленно следует, что

HA) | 6 exp( - p i ^ * (ln | A | )),    | A | = r n n Е N.

Последнее же возможно лишь для ^ = 0.

Далее, образуем подпоследовательности Лп : = (Ank)kGz вещественных нулей функции L, где Ank = 2nk + 2n—1 — 1 (n Е N). Как нетрудно видеть, любые две такие подпоследовательности не имеют одинаковых элементов. Заметим также, что Лп является последовательностью всех нулей функции gn(A) := sinп^^П + 2П — ^j. Положим Ln(A) := nm=i gm(A)f (A) и Щ := (1 — 2)п (n Е N), где gm (A) := sin ni( — +

-

^m           2 ^m 2 ^m

Тогда из свойств функции L следует, что при каждом n ∈ N:

• (I)    Существует такая последовательность (R _nm ) “ =1 , R _nm t го при m ^ го , что In | L n (A) | = Hr „ (A) + O(1), | A | = R nm , m -го ;

• (II)    In | L n (A nk ) | = H n n (A nk ) + O(1) при k ^ го .

Следует отметить, что в последовательность Л _п (n Е N) заведомо не попали точки A s := 2 ^s — 1 (s Е N, s >  n), являющиеся нулями функции L.

Для каждого n ∈ N образуем целую функцию

∞

L ⁰ (A) :=П(1 —

λ

,

2 ^s — 1

имеющую нулевой порядок. Положим

T s := {A Е C : || A | — A _s | 6 1}, s Е N; ∞

T := JT; s(A):=[log ₂ ( | A | + 1)], A Е C, s=1

и рассмотрим произвольное A, лежащее вне T . Ясно, что 2 ^s(A) <  | A | < 2 ^s(A)+1 — 2. Тогда при достаточно большом A / T (например, при | A | >  2 ⁿ⁺² — 1) имеют место следующие оценки

s(A)                   X ln |L0(A)| = £ln 1 — —- n                   2s — 1

∞

λ

2 ^s — 1

s(A)

> X ^ln

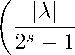
⁺ X ^ln s=s(A)+1

∞

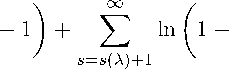
+ X ln 1 — s=s(A)+1    \

-

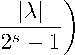
2 ^s(^⁾⁺¹ — 2

2 ^s — 1

s(A)

> X ^ln

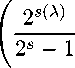
— 1

Отметим, что ln ( 2^—1 — 1) >  (s(A) — s) ln2 — 1 при s 6 s(A) — 1, и ряд

∞

X ln 1 — s=s(A)+3

∞

v       /

= / ln 1

s=1

-

2 s

сходится, причем его сумма не зависит от λ. Поэтому, учитывая очевидные соотношения In | А | /ln 2 — 1 6 s(A) 6 In | A | / ln 2 + 1, | A | >  1, получаем

s(A)-1                            ( 2sW       \ ln Ln(A)| > У ((s(A) — s)ln2 — 1) + ln f 2s

(    2-'^Л" — 2\      (    2s(^x)+i — 2\      “      /        1    \

^{+ ln}I ^{1 —}2s(^)+1 — 1 ) ^{+ ln} ( ^{1 —}2sW+2 — 1 J ⁺ X ^ln ( ^{1 —}2s-sto-2 )

s=s(A)+3

= --(—ln2 ■ O(s(A)) = ^ + O(ln |A|). 2                      2 ln 2

Кроме того, аналогичные оценки, проведенные для A с |A — As| = 1, показывают, что ln |(УПУ >      + O(ln |AsD при s ^^-

• ⁿ           2 ln 2

С другой стороны, для любого достаточно большого A G C (например, |A| > 2ⁿ⁺¹— 1)

S(A)

ln |L⁰(A)| 6 Vln(1 + U У ln(1 +

• ⁿ                   2^s— 1                      2^s— 1

s=n     '             '    s=s(X)+1     '

s(A)                                        +c           /             1       \s

6 £ln(1+2-

• = s+n^(s(A) — n + 1) ln 2 + O(s( A)) =      + O(ln |A|).

• 2                                          2 ln 2

Положим Ln(A) := Ln(A) Ln^A) (n G N) и обозначим через Л_п простые нули этой функции — {Amk : k G Z, 1 6 m 6 n} U {As : s > n}.

Из асимптотических оценок, установленных выше, получаем, что ln |Ln(A)| 6 Hnn(A) + o + O(ln |A|), A G C, A ^ ro, n 2 ln 2

ln |Ln(A)| > Hnn(A) + ln ^|A| + O(ln |A|)   при |A| = 2^s+ ¹, s ^ ro,

2 ln 2                                 2

и

ln |Ln(A)| = Hnn(A) + ^lnp^A+ O(ln |A|) при A G Л_п, A ^ ro. ^{n n}2 ln 2

Отсюда следует, что при po := 2/ ln2 и ^o(t) := t²(при этом ясно, что ^о G W и что +0(t) = t²/4) E(Л_п) является минимальной для A^p°0)(П_п) системой, для которой выполнены все условия следствия 1. В соответствии с ним E(Л_п) является АПС в А^р°0)(П_п) при всех n G N. Так как Л_п С Л, то E(Л) также является АПС в А^р°0)(П_п) при всех n G N. Заметим, что при этом последовательность квадратов (nn)n‘=1 исчерпывает П изнутри.

Таким образом, мы построили систему экспонент, которая не обладает свойством устойчивости относительно предельного перехода по области для пространств вида AP а(П).

(^)V