Minimax Estimation of the Parameter of Exponential Distribution based on Record Values

Published Online February 2014 in MECS

Record values and the associated statistics area of interest and important in many real life applications involving data relating to meteorology, sport, economics and life testing.

Set

Yn = max{X1,X2,™,Xn},n > 1, we say that X is an upper record and denoted by

X u ( j ) if Y j > Y - 1 , j > ^{1 .}

The detail about record values can refer Arnold et al.(1998), Raqab (2002), Jaheen (2004) and Ahmadi et al.(2005) and references therein.

Exponential distribution is one of the most commonly used models in life-testing and reliability studies. Inferential issues concerning the exponential distribution, and applications in the context of lifetesting and reliability, have been extensively discussed by many scholars. A great deal of research has been done on estimating the parameters of the exponential distribution using both classical and Bayesian techniques. See for example Bain (1978), Chandrasekar et al. (2002), Jaheen (2004), and Ahmadi et al. (2005) and references therein.

This paper is devoted to the minimax estimation problem of the unknown scale parameter 6 in the exponential distribution with probability density function (pdf)

f ( x ; 66 = 6 exp(- 6 x),   x >  0, 6 >  0        (1)

and cumulative distribution function(cdf)

F ( x ; 6 ) = 1 - exp(- 6 x),   x >  0, 6 >  0       (2)

where f ( x ; 6 ) denotes the conditional pdf of random variable(r.v.)X given 6 .

This paper will discuss the minimax estimation of the parameter of exponential distribution based on record values.

• II.    Preliminaries

  • 2.1    Maximum Likelihood Estimation

Let X_x , X ₂, ™ be a sequence of independent and identically distributed (iid) random variables with cdf F ( x ; 6 ) and pdf f ( x ; 6 ) .

In the following discussion, we always suppose that we observe n upper record values

XU (1) = x1, XU (2) = x 2,™, XU (n) = xn drawn from the exponential model with pdf given by (1).

The joint distribution of Xv(1),X^2),™,Xu(n^ is given (see Arnold et al. (1998)) by n-1

f ,2_ n ( x ; 6 ) = f ( x „ ; 6 ) П h ( x ; 6 ),

= 1

0 < x1 < • ■ • < xn

Where x = ( x , x ₂,

•, x n ), h ⁽ x i ; ^{6 )} =

f ( x ; 6 )

1 - f ( xt ; 6 )

Since the marginal pdf of X    is given (see Arnold et al. (1998)) by fn(xn;θ)=f(xn;θ)[-ln(1-F(xn;θ)]n-1 (n-1)!

=¹ θ ⁿx^{n - 1} e ^{- θ xn} , x > 0

Γ ( n )     ⁿ

Thus

XU(n) ~Γ(n,θ), and

EX U ( n ) = n / θ

The likelihood function based n upper record values is given by

l(61 x) = f,2_n(x6) = ^n exp(-6xn)(5)

and the log-likelihood function may be written as

L(θ|x) =lnl(θ|x) =nlnθ-θx(6)

Upon differentiating (6) with respect to θ and equating each results to zero, the MLE of θ is given by d ln L(θ | x)

_{d θ}    = _θ - x_n =

Then ， the MLE of θ is

ˆ ⁿ

δMLE =

^XU ( n )

• 2.2    Loss Function

  In statistical decision theory and Bayesian analysis, loss function plays an important role in it and the most common loss are symmetric loss function ,especially squared error loss function are considered most. Under squared loss function, it is to be thought the overestimation and underestimation have the same estimated risks. However, in many practical practical problems, overestimation and underestimation will have different consequences. To overcome this difficulty, Varian(1975)and Zellner(1986)proposed an asymmetric loss function known as the LINEX loss function, Podder et al.(2004) proposed a new asymmetric loss function for scale parameter estimation. See also Kiapou ra and Nematollah ib( 2011), Mahmoodi, and Farsipour(2006). This loss function is called squared log error loss(SLE) is

L ( θ , δ ) = (ln δ - ln θ )²                     (8)

Which is balanced and L ( θ , δ ) → ∞ as δ → 0 or ∞ . This loss is not always convex, it is convex for ^δ

≤ e and concave otherwise, but its risk function has θ, minimum w.r.t.

δ ^ˆ _SL = exp[ E (ln θ | X )] .

In many practical situations, it appears to be more realistic to express the loss in terms of the ratio θ / θ . In this case, Dey et al. (1987) pointed out that a useful asymmetric loss function is entropy loss function:

L ( θ ^ˆ, θ ) = ^δ - ln ^δ - 1                     (9)

θθ

Whose minimum occurs at δ = θ . Also, this loss function has been used in Singh et al. (2011), Li and Ren(2012) .The Bayes estimator under the entropy loss is denoted by θ , given by

δ ^ˆ BE = [ E ( θ ^{- 1} | X )] ^{- 1}.                         (10)

• III.    Bayes Estimation

In this section, we estimate θ by considering weighted square error loss, squared log error loss and entropy loss functions.

We further assume that some prior knowledge about the parameter θ is available to the investigation from past experience with the exponential model. The prior knowledge can often be summarized in terms of the so-called prior densities on parameter space of θ . In the following discussion, we assume the following Jeffrey’s non-informative quasi-prior density defined as,

π ( θ ) ∝ ¹ _d , θ > 0 (11) θ

Hence, d = 0 leads to a diffuse prior and d = 1 to a non-informative prior.

Combing the likelihood function (5) and the prior density(10),we obtain the posterior density of θ is n-d+1

h ( θ | x ) =     ^{x n}         θ ^{( n - d + 1) - 1} e ^{- θ xn}        (12)

Γ ( n - d + 1)

This is a Gamma distribution. Γ ( n - d + 1, x ) , where x is the observation of X .

Theorem3.1. Under the weighted square error loss function

L 1 ( θ , δ ) = ^{( δ -} 2 ^{θ ) 2}                        (13)

θ

Then (i) the Bayes estimator under the weighted square error loss function is given by

E [ θ ^{- 1} | X ] n - d - 1

δ ==         (14)

^BS    E [ θ ^{- 2}| X ]      X U ( n )

E (ln θ | X )

n - d + 1

₌     ^XU ( n )       ^∞ _{ln θ ⋅ θ} ( n - d + 1) - 1 _e

Γ ( n - d + 1) ⁰

= ^d ln Γ ( n - d + 1) - ln X U ( n ) dn

=Ψ ( n - d + 1) - ln X U ( n )

Where

d          +∞ ln y ⋅ y

Ψ ( n ) =    ln Γ ( n ) =∫ ₀

dn

-

θ X U ( n ) _{d θ}

n - 1 e

Γ ( n )

- y dy

(ii) the Bayes estimator under the squared log error loss function is come out to be

Ψ ( n ) δ ^ˆ SL = exp[ E (ln θ | X )] = ^e               (15)

^XU ( n )

is a Digamma function.

Then the Bayes estimator under the squared log error loss function is come out to be

e δ ^ˆ _SL = exp[ E (ln θ | X )] =

Ψ ( n - d + 1)

^XU ( n )

.

• (iii)    the Bayes estimator under the entropy loss function is obtained as

δ ^ˆ BE = [ E ( θ ^{- 1}| X )] ^{- 1} = ^{n - d}               (16)

X

• (iii)    By Eqs.(10) and (17), the Bayes estimator under the entropy loss function is given by

δ ^ˆ BE = [ E ( θ ^{- 1} | X )] ^{- 1} = ^{n - d} .

^X U ( n )

Proof. (i) by formula (11),we know that

θ | X   Γ ( n - d + 1, X U ( n ) ) ,

Then

E [ θ ^{- 1} | X ] = ^{X U ( n )}, n - d

X ²

E [ θ ^{- 2} | X ] =          ^{U ( n )}

( n - d )( n - d - 1)

Thus, the Bayes estimator under the weighted square error loss function is given by

_ˆ      E [ θ ^{- 1} | X ]

^BS    E [ θ ^{- 2} | X ]

X _{U ( n )} /( n - d )        n - d - 1

X U ² ( n ) /( n - d )( n - d - 1)     X U ( n )

• IV.    Minimax Estimation

The most important elements in the minimax approach are the specification of the prior distribution and the loss functions by using a Bayesian method.

The derivation of minimax estimators depends primarily on a theorem due to Lehmann which can be stated as follows:

Lemma4.1 ( Lehmann’s Theorem ) If τ = { F ; θ ∈ θ} be a family of distribution functions and D a class of estimators of θ .Suppose that δ ^• ∈ D is a Bayes estimator against a prior distribution δ ^• ( θ ) on θ , and R ( δ ^• , θ ) equals constant on Θ ; then δ ^• is a minimax estimator of θ .

Theorem 4.1 Let X_T , X^ , _ , X_n be a random sample drawn from the density (1),

(ii) Using (12),

n - d - 1 then δ =

^BS     X U ( n )

is the minimax estimator of

the parameter 6 for the weighted square error loss function of the type (13).

Theorem 4.2 Let Х_г , X ₂,..., X_n be a random sample drawn from the density (1),

V ( n - d + 1)

then 5_V =-------- is the minimax estimator of

^XU ( n )

the parameter 6 for the squared log error loss function of the type (8).

Theorem 4.3 Let Хг,X2,...,Xn be a random sample drawn from the density (1), a n - d then onj, =------ is the minimax estimator of the

BE

^XU ( n )

parameter 6 for the entropy loss function of the type

Then

R ^{( 6 )} = J

( n - d - 1)²

( n - d )( n - 2)

- 26(n - d -1)-----+ 6^

n - d

^  2 n — d — 1   ( n — d — 1)

n - d ( n - d )( n - 2)

Then R ( 6 ) is a constant .So, according to the

- n - d -1

Lehmann’s theorem it follows that, 5_n(, =--------- is

, BS

^XU ( n )

the minimax estimator for the parameter 6 of the exponential distribution under the weighted square error loss function of the form (12).

Now we are going to prove the theorem4.2. The risk function of the estimator 5SL e V (n - d+1) is

Y

^XU ( n )

Proof. First we have to prove the theorem 4.1. To prove the theorem we shall use Lehmann’s theorem, which has been stated before.

For this, first we have to find the Bayes estimator 5 of 6 . Then if we can show that the risk of d is constant, then the theorem3.1 will be proved.

R(6) = E[L(<5 )] = E (ln 5>sl - ln 6)

= E [ln 5_S J² - 2ln 6 • E ln[< 5_sL ] + (ln 6 )²

is

The risk function of the estimator 5_n(, =--------

BS ^XU ( n )

R( 6 ) = E L 6 , n-d- 1

= E

^{( n - d -} 1) / X U ( n )

- 6 Y

From the conclusion Х _У(_n) ~ Г( n , 6 ) ,we have

E (ln X u ( n ) ) = V ( n ) - ln 6

Thus

E [ln 5 _Sl ] = E ( V ( n - d + 1) - ln X u ( n ) )

= V ( n - d + 1) - ( V ( n ) - ln 6 )

= V( n - d +1)-V (n) + ln 6

= 5г [ ( n - ^d - 1) 2 ^E ( X U 2 . ) )

—

--1

U ( n )

From the conclusion X ^„) ~ Г ( n , 6 ) ,we have

E ( X n ) ) =

E ( X u 2 n ) ) =

n-1, 62

( n - 1)( n - 2)

E [ln 5 _SL ]² = E ( V ( n - d + 1) - ln Xu ( n ) ) 2

= V ²( n - d + 1) - 2 V ( n - d + 1) E (ln X_{u( m} )

+ E [(ln Xu ( n ) ) 2 ]

Using the fact

• n ) _=r ⁽ ln у )² У- ' e- y dy

^J 0       Г ( n )

• -Г (lny^^yv ^{- 1}- V ( n ) dy , ^J 0       Г ( n )

= E [(ln Y )²] -V ²( n )

where Y ~ Г( n ,1) .and we can show that

Y = X u ( n ) 9 ~ Г( n ,1)

Thus

T ²( n ) + T' ( n )

= E [(ln Y )²] = E [(ln X u ( n ) + ln 9 )²]

= E [(ln X u ( n ) )² ] + 2ln 9 • E (ln X u ( n ) ) + (ln 9 )²

= E [(ln X U _{( n} ) )² ] + 2ln 9 • ( T ( n ) - ln 9 ) + (ln 9 )²

Then we get the fact

E [(ln X u ( n ) )²] = T ²( n ) + T' ( n )

- 2ln 9 ^T ( n ) + (ln 9 )²

Therefore

E [ln 5 SL ]²

= T ²( n - d + 1) - 2 T ( n - d + 1) E (In X_U(n) )

+ E [(ln X u ( n ) )²]

= T ²( n - d + 1) - 2 T ( n - d + 1)[ T ( n ) - ln 9 ]

+ T ²( n ) + T' ( n ) - 2ln 9 • T ( n ) + (In 9 )²

^R ( ⁹ )

= E [In 5_S J² - 2ln 9 • E ln[ 9_sL ] + (In 9 )²

= T ²( n - d + 1) - 2 T ( n - d + 1)[ T ( n ) - In 9 ]

+ T ²( n ) + T' ( n ) - 2ln 9 • T ( n ) + (In 9 )²

- 2ln 9 • [ T ( n - d + 1) -T ( n ) + In 9 ] + (In 9 )²

= T ²( n - d + 1)

- 2 T ( n ) T ( n - d + 1) + T ²( n ) + T' ( n )

Then R( 9 ) is a constant. So, according to the

„      e ^T ( n - ^d + 1)

Lehmann’s theorem it follows that, 9, =--------- is

SL

^XU ( n )

the minimax estimator for the parameter 9 of the exponential distribution under the squared log error loss function of the form (8).

X U ( n )

^R 9 ) = ^E [ ^L ( 6 , ) ]

= E

n - d

E n - d eXU^

- ln

n - d

9 X u ( n )

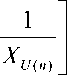
- ln( n - d ) + ln 9 + E [ln X_{u( n)} ] + 1

= n - d - ln( n - d ) + ln 9 + T ( n ) - ln 9 + 1 n - 1

= n - d - ln( n - d ) + T ( n ) + 1

n - 1

Then R (9) is a constant .So, according to the a n - d Lehmann’s theorem it follows that, onj, =------ is

BE

^XU ( n )

the minimax estimator for the parameter 9 of theexponential distribution under the entropy loss function of the form (9).

• V.    Risk Function

The risk functions of the estimators 9DC, 9, and 9ЯГ. BS BL     BE relative to squared error loss

L ( 9 ), 9 ) = ( 9 - 9 ) ²

are denoted by R(9)BJ,R(9ДJ and R(9BE) , respectively, are can be easily shown as

R ( i > _B5 ) = E [ L ( 9 > BS , 9 )]

= E[(<9BS -9)2] = E[(’n-X-1 -9)2] X ro

Jo

(n -d -1)2  2(n -d -1)9

-----2+ xx

•» (n -d -1)2  2(n -d -1)9

0      x2x fXu (n,( x ) dX

n

—x n ^{- 1} e -^9xdx ,

Г ( n )

= 9

( n - d - 1)²   2( n - d - 1)

( n - 1)( n - 2) n - 1

„ T( n - d + 1)

A              A                       D '      '

R ( ё SL ) = E [ sL - 0 ) 2 ] = E [(—-- 0 ) 2 ]

^XU ( n )

го

^J o

^

^J o

= 0²

2 V ( n - d + 1)

2 2 T ( n - d + 1)

2 e t ⁽ n - d + 1) 0

x

+ 0 ² f_Xu ( x ) dx

n

—xn ^{- 1} e ""dx

Г ( n )

2 V ( n - d + 1)       2^^ ( n - d + 1)

----+1

( n - 1)( n - 2) n - 1

R (< ? BE ) = E [ L ( 6 _B e , 0 )]

= E [(< ? BE - 0 ) 2 ] = E [( n - d - 0 ) 2 ] ^XU ( n )

го

^J 0

( n - d )²  2( n - d ) 0 _{+ y2}

_x 2          _x

f-u ( . ) ( x ) dx

;• [ ( n# - ^+ 0 1 ^i x ' - e-^

⁰ [    x²          x           Jf< n )

= 0²

( n - d )²     2( n - d )   '

( n - 1)( n - 2)     n - 1

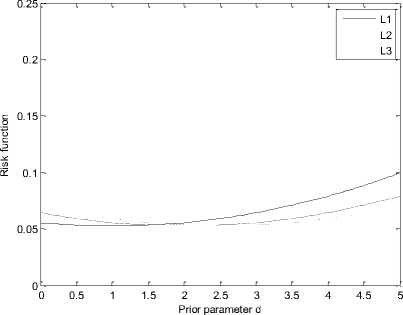
Fig. 2: Ratio of the risk functions with n=20

0.25

0.2

0.15

0.1

0.05

L1

L2

L3

0     0.5     1      1.5     2     2.5     3     3.5     4     4.5     5

Prior parameter d

In the Fig.1-4, we have plotted the ratio of the risk functions to 0 ² ,i.e.

Fig. 3: Ratio of the risk functions with n=30

0.25

A

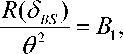
. A .

R ( ^ >s l)   _n

— = B ₂ , and

R ( ё в, )

= B 3

0.2

L1

L2

L3

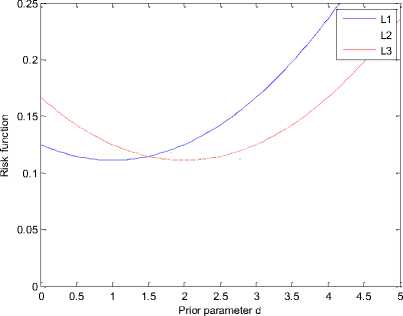
Fig. 1: Ratio of the risk functions with n=10

0.15

0.1

0.05

0     0.5     1      1.5     2     2.5     3     3.5     4     4.5     5

Prior parameter d

Fig. 4: Ratio of the risk functions with n=50

From Fig.1-4, it is clear that no of the estimators uniformly dominates any other. We therefore recommend that the estimators be chosen according to the value of d when the quasi-prior density is used as the prior distribution, and this choice in return depends on the situation at hand.