Минимизация бинарных переключательных функций в базисах 2и-не, 2и-2или-не

В связи с известными проблемами в области создания современной отечественной электронной компонентной базы при проектировании радиоэлектронной аппаратуры (РЭА) специального назначения широко применяются так называемые полузаказные цифровые интегральные микросхемы на основе базовых матричных кристаллов – БМК. В открытых источниках упоминаются БМК серий 5503, 5507, 5521, 5528, 5529, причем их основой являются так называемые ячейки поля БМК, представляющие собой 4-унифи-цированные транзисторные структуры КМДП (КМОП) транзисторов.

Для получения цифровых устройств необходимо создать фотошаблон для задания соответствующих связей ячеек. Конечно, проектные нормы и степень интеграции таких микросхем значительно отстают от технологических показателей передовых западных фирм, но, как говорится, зато своевременно.

Для создания радиационно-стойкой, надежной, отказоустойчивой электронной компонентной базы необходима избыточность, например дублирование, троирование, рас-

четверение (по терминологии патентной классификации). При троировании, которое еще называют мажоритированием, битовые выходы трех каналов цифрового автомата поступают на три входа мажоритарного элемента, реализующего мажоритарную функцию или функцию голосования по большинству голосов (выбора "два из трех" ≥2). Мажоритарный элемент широко применяется для обеспечения пассивной отказоустойчивости цифровых устройств и систем. При этом резервирование с целью обеспечения пассивной отказоустойчивости обеспечивает выигрыш не на всем временном интервале для некоторого интервала вероятностей.

Предложены транзисторные структуры, парирующие отказы (сбои) части транзисторов, возникающие в результате воздействия радиации и других негативных факторов.

Вначале они рассматривались в качестве так называемых функционально-полных толерантных (ФПТ) элементов (ФПТЭ), сохраняющих при отказах либо функциональную полноту (ФПТ в слабом смысле), либо реализуемую логическую функцию (ФПТ в сильном смысле). В дальнейшем подобное резервирование транзисторных структур (ТС) – ФПТТС в сильном смысле и ФПТТС предложено использовать не только в КМОП (КМДП) струк- турах, но и в структурах на основе передающих МДП транзисторов.

В отличие от канального резервирования цифровой аппаратуры, такое резервирование названо потранзисторным , что обеспечивает по сравнению с троированием значительный выигрыш в вероятности безотказной работы пассивно отказоустойчивой схемы практически для всего временного диапазона.

Для парирования одного отказа (сбоя) в ТС необходимо 4 транзистора и так называемое "расчетверение" на транзисторном уровне. Такая избыточность в принципе требует и резервирования связей, а также наталкивается на существенное ограничение в количестве последовательно соединенных транзисторов, стандартное значение которого, как правило, равно четырем. Уже имеется информация, что современные технологии несколько смягчают это ограничение до пяти и даже до шести последовательно соединенных транзисторов.

Однако исследований по созданию избыточных ячеек БМК в достаточной мере не проводилось.

Как известно, большое значение для решения проблемы создания отечественной элементной базы имеет инновационный комплекс Московского института электронной техники (МИЭТ) [1, 2], в котором значительное внимание уделяется созданию полузаказных цифровых интегральных микросхем на основе базовых матричных кристаллов – БМК [3–7].

КМОП-схемотехника БМК имеет относительно невысокое быстродействие, задержки КМОП-вентилей на порядок больше, чем для ЭСЛ. Но неоспоримыми достоинствами КМОП-схемотехники являются малая потребляемая мощность и высокая помехоустойчивость [4].

Несмотря на значительное отставание в технологических нормах, по сравнению с передовыми западными фирмами, наша электронная промышленность в целом пока позволяет создавать цифровую аппаратуру для специальных приложений [8–10].

В настоящее время открытые источники сообщают о БМК серий 5503, 5507, 5521, 5528, 5529 [3].

Ячейка поля БМК представляет собой 4-транзисторную ячейку комплиментарных транзисторов [3] (рис. 1).

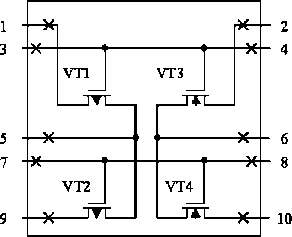
Рис. 1. Ячейка поля базового матричного кристалла – БМК

Из таких ячеек строятся логические элементы, например [7]. Для создания радиационно-стойкой аппаратуры [11–12] ранее автором было предложено расчетверение отдельных транзисторов логических элементов, что обеспечивает по сравнению с резервированием каналов цифровой аппаратуры значительный выигрыш в вероятности безотказной работы пассивно отказоустойчивой схемы практически для всего временного диапазона [13–19]. Однако имеется ограничение на число последовательно соединенных транзисторов [20]. Отмечено, что в последнее время активно развивается научное и технологическое направление создания высоконадежных, радиационно-стойких микросхем для космических, специальных и военных применений.

Для обеспечения надежности таких специальных микросхем применяют троирование – TMR (Triple Modular Redundancy), которое позволяет парировать не только ошибки (ранее именовавшиеся сбоями) – SEU (Single Event Upset), но и отказы SEE (Single Event Effect) – в одном из трех каналов [1, 2]. Одним из самых опасных подвидов SEE является защелкивание транзисторов (single effect latchup, SEL) в пропускающем состоянии (тиристорный эффект). Метод тройного резервирования для ячеек памяти (Triple Modular Redundancy, TMR) или мажоритирования [2, 3] показан на рис. 2.

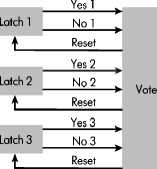
Рис 2. Ячейка статической оперативной памяти SRAM, предотвращение SEU методом троирования – тройного резервирования

1. Отказоустойчивая ячейка поля БМК

Для этого пару ячеек (рис. 1) конфигурируем для реализации одного резервированного транзистора р- типа в соответствии с [13– 19] и одного резервированного транзистора n- типа (см. рис. 3).

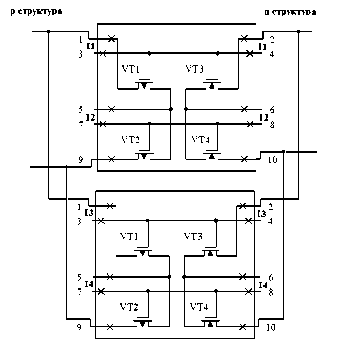
Рис. 3. Отказоустойчивая ячейка поля базового матричного кристалла – БМК для реализации f 12 = x i x i _v x i x i одного транзистора р-типа и одного транзистора n-типа

При этом каждый транзистор управляется своим сигналом I1–I4 (3, 7), которые подаются с двух сторон ячейки, что требует рас-четверения связей. Если объединить входы, получим рис. 5.

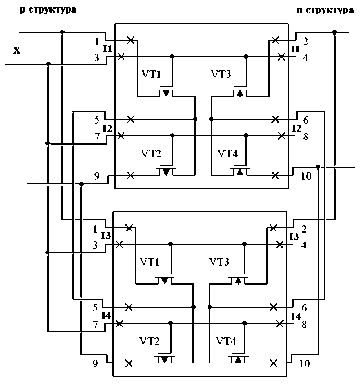
р ис . 5. Отказоустойчивая ячейка поля базового матричного кристалла – БМК для реализации f ₁ = (x _{v x} )(_{x v x} ) одного транзистора р-типа и одного транзистора n-типа с объединением входов Х

Такая ячейка сохраняет работоспособность при отказе одного любого транзистора р типа и одного любого транзистора n -типа ценой четырехкратной избыточности. Если реализовать функцию f_H = (x i v x₁)(x₁ v x i ) , т.е. перемычку по точкам 5, 6, то получим рис. 4.

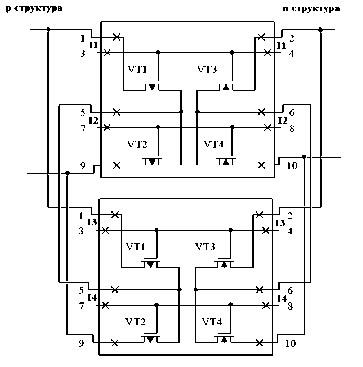
Рис. 4. Отказоустойчивая ячейка поля базового матричного кристалла – БМК для реализации f _} = (_{x v x}. )(_x. _{v xj}) одного транзистора р-типа и одного транзистора n-типа с перемычкой по точкам 5, 6

Наконец, если вход Х продублировать с другой стороны ячейки, получим рис. 6.

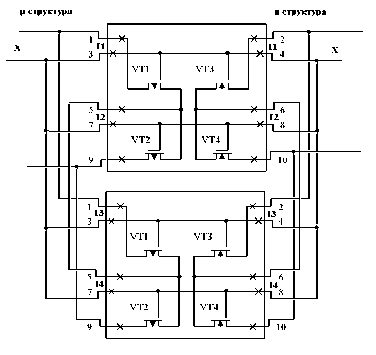
р ис . 6. Отказоустойчивая ячейка поля базового матричного кристалла – БМК для реализации f = (_{x v x} )(_{x v x} ) одного транзистора р-типа и одного транзистора n-типа с объединением входов и дублированием Х

• 3.    Реализация отказоустойчивой ячейки оперативной памяти SRAM – QSRAM

Построим отказоустойчивый инвертор, например, для радиационно-устойчивой ячейки оперативной памяти SRAM (рис. 7).

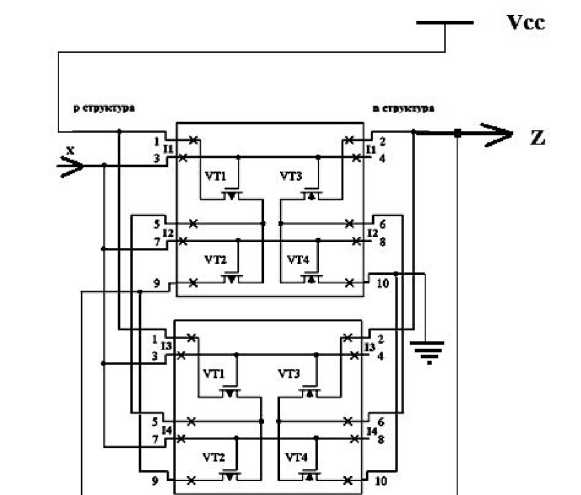
Рис. 7. Отказоустойчивый инвертор для ячейки оперативной памяти SRAM

Тогда ячейка оперативной памяти SRAM [21–24], состоящая из двух инверторов, будет выглядеть так, как показано на рис. 8.

В перспективе рекомендуется провести исследования с учетом особенностей топологии кристалла и интенсивности отказов связей.

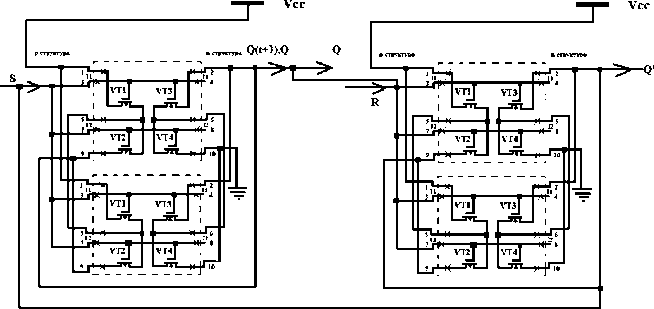
Рис. 8. Отказоустойчивая ячейка оперативной памяти SRAM – QSRAM

Аналогично могут быть резервированы и транзисторы записи, считывания ( " боковые " транзисторы).

Модель отказоустойчивой ячейки оперативной памяти SRAM – QSRAM представлена на рис. 9.

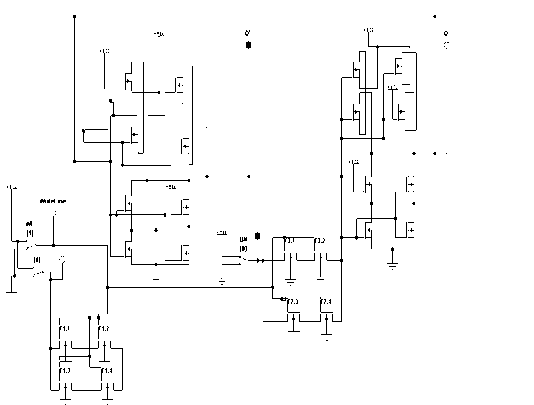
Рис. 9. Модель отказоустойчивой ячейки оперативной памяти SRAM – QSRAM в системе схемотехнического моделирования NI Multisim

Выводы

Таким образом, на основе двух 4-транзисторных стандартных ячеек разработана отказоустойчивая ячейка поля БМК, которая представляет собой две резервированных структуры для реализации одного транзистора р -типа, и одного транзистора n -типа. В частности, линии управления затворами всех транзисторов могут быть объединены. Такие ячейки целесообразно использовать для проектирования высоконадежной [25] аппаратуры на основе БМК. Предложенная ячейка статической оперативной памяти QSRAM с учетверением транзисторов на основе ячеек БМК парирует отказы типа SEU (Single Event Upset) и SEE (Single Event Effect).

Сравнение показывает существенно больший выигрыш в вероятности безотказной работы по сравнению с троированием, причем затраты на троирование одной ячейки при одном мажоритаре равны 3*6+10=28 транзисторов (задержка в числе транзисторов без учета "боковых" транзисторов равна 4), а в предложенной ячейке затраты равны 24, задержка такая же – 4. В случае троирования мажори-таров затраты равны 3*6+3*10=48.