Минимизация эмпирического риска при построении монотонных композиций классификаторов
Автор: Гуз И.С.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Математика, управление, экономика
Статья в выпуске: 3 (11) т.3, 2011 года.
Бесплатный доступ
В работе описывается метод обучения монотонного классификатора, минимизиру- ющий эмпирический риск. На основе этого метода синтезируется монотонная ком- позиция, построенная над результатом работы нескольких независимо обученных алгоритмов. Проводится исследование качества классификации монотонной компо- зиции на реальных задачах в зависимости от числа и типа алгоритмов, входящих в ее состав.
Короткий адрес: https://sciup.org/142185760
IDR: 142185760
Текст научной статьи Минимизация эмпирического риска при построении монотонных композиций классификаторов
При решении прикладных задач классификации очень часто возникает ситуация, когда ни один из существующих алгоритмов в отдельности не решает задачу с достаточным качеством. В таких случаях пытаются учесть сильные стороны каждого отдельного алгоритма за счет построения из них некоторой композиции.
В работе рассматривается проблема повышения качества классификации при помощи построения алгоритмических композиций для задач, описываемых некоторой выборкой объектов, где каждый объект принадлежит одному из двух непересекающихся классов, –1 и +1. Предполагается, что существует набор базовых алгоритмов, независимо обученных на заданной выборке. Причем каждый базовый алгоритм определяет для каждого объекта не только его класс, но и оценку принадлежности классу +1. Этим свойством обладают многие известные алгоритмы классификации, например, байесовские классификаторы, нейронные сети, логистическая регрессия, дерево решений CART и другие. В байесовских классификаторах оценка принадлежности интерпретируется как апостериорная вероятность того, что объект принадлежит классу +1. Однако в данной работе никаких предположений о вероятностной природе данных не делается, и оценки принадлежности интерпретируются в более широком смысле. Чем больше оценка, тем с большей уверенностью можно утверждать, что объект принадлежит классу +1.
В качестве алгоритмической композиции в работе рассматривается монотонная корректирующая операция [16], которая является монотонной функцией в пространстве оценок принадлежности. Использование монотонной функции оправдано тем, что если для одного объекта оценки принадлежности не меньше, чем для другого, то и оценка принадлежности первого объекта, рассчитанная с помощью композиции, должна быть не меньше, чем для второго. Монотонные корректирующие операции образуют более широкое семейство по сравнению с выпуклыми (линейными с неотрицательными коэффициентами), используемыми в методах голосования, в частности, в бу-стинге [19]. Это позволяет точнее настраиваться на данные и использовать существенно меньшее число базовых алгоритмов, но, как было показано в [1], повышает риск переобучения.
Известно несколько методов построения монотонной функции, точно или приближённо проходящей через заданные точки. Изотонная регрессия [2] позволяет рассчитать значение монотонной функции на каждом объекте таким образом, чтобы сумма квадратов разности значения класса и значения восстанавливаемой функции по всем объектам была минимальна. Этот метод предполагает непрерывность монотонной функции, и после его применения необходимо выбрать порог отсечения, при котором относить объекты к каждому из классов. Другой метод, описанный в [3], использует жадный алгоритм удаления объектов, нарушающих монотонность. Все эти методы являются эвристическими и не гарантируют минимум эмпирического риска, то есть числа ошибок классификации на обучающих данных.
Целью данной работы является конструктивное доказательство существования метода обучения монотонной корректирующей операции, минимизирующего эмпирический риск, а также исследование её обобщающей способности при решении прикладных задач.
-
I. Постановка задачи классификации на два класса
Пусть задано конечное множество X = { x i , x i , ..., x l } , состоящее из L объектов, в котором каждый объект x i описывается вектором из n вещественных признаков { x^, x 2 , ..., х П } Е R n . Этим объектам соответствует множество классов Y = { y o , y i , ..., y L -i } , в котором значения классов y i Е {- 1, + 1 } . Если для двух объектов x i и x j выполняется условие V к = 1, ..., n : x k > x j , то будем считать, что x i > x j . Если же 3 k, t : x k > x j , x i < x j , то будем считать, что объекты x i и x j несравнимы и будем обозначать x i \\ x j . Назовем множество X генеральной выборкой, и будем считать, что среди объектов нет двух одинаковых.
Пусть также задано множество A, элементы которого называются алгоритмами, где каждый алгоритм а Е A : R n ^ { — 1, + 1 } . Существует бинарная функция I : A х X ^ { 0,1 } , называемая индикатором ошибки. Если I (a,x) = 1, то алгоритм а Е A допускает ошибку на объекте x. Вектором ошибок алгоритма а Е A будем называть L-мерный бинарный вектор { I(a,X i ) } L =1 . В качестве множества алгоритмов A рассмотрим семейство монотонных алгоритмов классификации, то есть а Е A О ( V x i , x 2 Е R n : x i > x 2 ^ a(x i ) > a(x 2 )).
Методом обучения называется отображение ^ : X ^ A, которое ставит в соответствие генеральной выборке X некоторый алгоритм а Е A. Цель работы состоит в построении метода обучения µ, минимизирующего эмпирический риск, то есть в выборе такого монотонного алгоритма, для которого количество ошибок классификации на генеральной выборке минимально:
L
^(X) = argmin( > I (a,x i )).
a ∈ A i =0
-
II. Минимизирующий эмпирический риск монотонный классификатор
Будем считать, что все монотонные алгоритмы из множества A различимы на генеральной выборке X, то есть их векторы ошибок на выборке X попарно различны. В этом случае любой монотонный алгоритм а Е A полностью определяется двумя непересекающимися множествами:
Q = { x Е X : a(x) = +1 } ;
Q - = { x Е X : a(x) = — 1 } .
Эти множества должны обладать свойством, необходимым и достаточным для монотонности алгоритма a:
V x i Е ^ - , V x 2 Е Q : x 2 > x i V x 2 || x i (1)
Тогда задача метода обучения µ, минимизирующего эмпирический риск, состоит в построении таких множеств Q - и Q + , обладающих описанным выше свойством, для которых число ошибок монотонного классификатора минимально, то есть:
X [y i = +1] + X [y j = — 1 ^ min . (2)
x i ∈ Ω - x j ∈ Ω +
Назовем пару индексов (i,j ) дефектной, если выполняется одно из условий x i > x j , y i < y j или x i < x j , y i > y j .
Теорема 1. Сложн о сть обучения монотонного алгоритма a, минимизирующего эмпирический риск, равна O(mVd), где m — число дефектных пар, образованных объектами генеральной выборки X, а d — число объектов генеральной выборки, образующих дефект.
о На основе генеральной выборки X, а также информации о классах Y построим двудольный граф. Вершинами этого графа будут являться индексы объектов генеральной выборки, причем одна часть графа U - состоит из таких индексов j, для которых y j = — 1, а другая часть U + состоит из таких индексов i, для которых y i = +1. Ребро между вершинами с индексами (i,j)
будет существовать только в том случае, если (i,j) — дефектная пара. Поскольку дефектной может быть только пара, у объектов которой значения классов различны, то граф действительно получается двудольным (рис. 1).
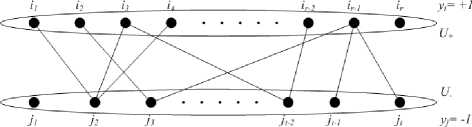
Рис. 1. Двудольный граф, отображающий все дефектные пары в генеральной выборке. Вершина графа — индекс объекта генеральной выборки, ребро графа — дефектная пара
Для построения множеств Q - и Q + для каждого объекта X i Е X введем булеву переменную u i , определяющую, будет ли на этом объекте ошибка:
Ui = 1 О (i Е U+ Л i Е Q-) V (i Е U- Л i ЕQ
Ui = 0 О (i Е U+ Л i Е Q+) V (i Е U- Л i Е
Тогда условие (2) запишется в виде
L
У^ ui ^ min .(3)
i =1
Заметим, что если две вершины i Е U + , j Е U - соединены ребром, то есть образуют дефектную пару, то это означает, что x i < x j . Если же они не соединены ребром, то это означает, что либо x i > x j , либо x i || x j .
Поэтому если вершина i Е U + является изолированной, то u i = 0 и i Е Q + . Аналогично если вершина j Е U - является изолированной, то U j = 0 и j Е Q - . После удаления изолированных вершин двудольный граф становится связным.
Чтобы было выполнено ограничение (1), необходимо, чтобы для каждой дефектной пары хотя бы на одном индексе допускалась ошибка. В терминах графа это требование означает, что необходимо выбрать вершины графа таким образом, чтобы каждое ребро было инцидентно хотя бы одной выбранной вершине. Условие (3) означает, что число таких вершин должно быть минимально. Таким образом, исходная задача по построению множеств Q - и Q + эквивалента задаче о минимальном вершинном покрытии в связном двудольном графе, образованном дефектными парами индексов генеральной выборки.
По теореме Кёнига [4] для связного двудольного графа задача о максимальном паросочетании сводится к задаче о минимальном вершинном покрытии. При этом сложность построения максимального паросо ч етания для двудольного графа в соответствии с алгоритмом Хопкрофта–Карпа [5] равна O(mVd). Здесь m — число ребер графа, то есть число дефектных пар, а d — число вершин графа, то есть число объектов, образующих дефект.
Воспользуемся методом построения монотонного алгоритма a , описанным в [15, 16], на основе множеств Q - и Q + :
a(z) = sign(p(z,Q + ) - p(z,Q - )).
Здесь множества Q - и Q + определены следующим образом:
Q + = { x i Е Q + : V X j Е Q + /x i X j > X i V X j || x i } — верхнее граничное множество;
Q - = { X i Е Q - : V X j Е Q - /X i X j < X i V X j || X i} — нижнее граничное множество.
Расстояния ρ от точки z до этих множеств равны
p(z,Q + ) = min (max([X 1 - z 1 ] + , [ x 2 - z 2 ] + , ..., [X n - z n ] + ));
X i GQ +
p(Q-,z) = min (max([z1 - X1]+,[z2 - x2] + , ..., [zn - Xn]+)), xieQ- где операция [x]+ обозначает x, если x > 0 и 0, если x < 0.
В [3] доказано, что построенный таким образом алгоритм a, действительно будет монотонным. •
Для пояснения метода обучения монотонного алгоритма, минимизирующего эмпирический риск, рассмотрим его работу на примере модельной задачи классификации (рис. 2 и рис. 3).
Отметим, что доказанный в теореме 1 метод построения монотонного алгоритма может быть также использован для улучшения оценки полного скользящего контроля для монотонных классификаторов, доказанной в [6], позволяя точно рассчитывать степень немонотонности конкретной выборки.
Рассмотрим теперь результаты применения монотонной корректирующей операции, минимизирующей эмпирический риск, при решении прикладных задач классификации.
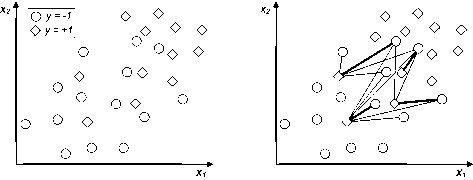
Рис. 2. На графике слева изображена двумерная генеральная выборка. Справа на объектах, образующих дефект, построен двудольный граф, и для него найдено максимальное паросочетание (выделено толстыми линиями)
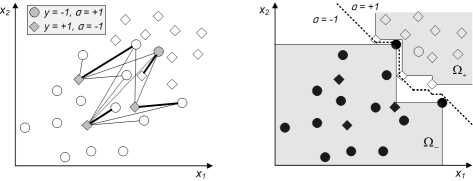
Рис. 3. На графике слева на основе максимального паросочетания построено минимальное вершинное покрытие (вершины выделены серым), определяющее состав множеств ^ - и □ + . Справа на основе этих множеств построен монотонный алгоритм a . Ломаная, разделяющая области значений — 1 и +1 этого алгоритма, выделена пунктиром
-
III. Эксперименты и результаты
Численные эксперименты проводились на четырех бинарных задачах классификации из репозитория UCI, различающихся как по числу объектов, так и по трудности их решения: Ionosphere, 351 объект; Spambase, 4601 объект; Musk (Version 2), 6598 объектов; Adult, 48842 объекта.
В качестве базовых алгоритмов классификации, определяющих для каждого объекта не только его класс, но и вероятность отнесения к этому классу, использовались следующие классические алгоритмы: решающие деревья С50 [7], CART [8], QUEST [9], CHAID [10]; нейронная сеть на основе многослойного персептрона [11]; k ближайших соседей [12], логистическая регрессия [13] и SVM с автоматическим выбором функции ядра [14].
В качестве композиции использовалась рассматриваемая в данной работе монотонная функция (Monot), которая сравнивалась с двумя другими классическими композициями. В качестве первой использовался алгоритм голосования вероятностями за каждый из классов (Voting), который относит объект к тому классу, за который сумма вероятностей базовых алгоритмов больше. В качестве второй использовался алгоритм, который относит объект к тому классу, вероятность отнесения к которому максимальна среди всех базовых алгоритмов (max).
Каждая из четырёх рассматриваемых задач случайным образом разбивалась на 2 выборки — обучающую, содержащую 70% объектов, и контрольную, содержащую 30% объектов. Каждый базовый алгоритм независимо от других обучался на обучающей выборке и затем применялся ко всем объектам обеих выборок для расчета вероятностей отнесения к обоим классам. Поверх этих оценок для обучающей выборки строилась монотонная функция, описанным в теореме 1 способом, которая затем также применялась для классификации всех объектов обоих выборок. Для двух других композиций не требуется обучение, поэтому они были сразу применены ко всем объектам, после обучения и применения базовых алгоритмов.
На рис. 4 приведены частоты ошибок рассматриваемых базовых алгоритмов и композиций, усредненные по 100 различным разбиениям, на обучающую и контрольную выборки (crossvalidation) для каждой из 4-х задач.
|
lonos |
phere |
Musk |
Spambase |
Adult |
||||
|
Обучение |
Контроль |
Обучение |
Контроль |
Обучение |
Контроль |
Обучение |
Контроль |
|
|
050 |
0,019 |
0,104 |
0,015 |
0,038 |
0,042 |
0,080 |
0,123 |
0,135 |
|
CART |
0,100 |
0,125 |
0,080 |
0,085 |
0,103 |
0,113 |
0,161 |
0,161 |
|
QUEST |
0,108 |
0,134 |
0,098 |
0,101 |
0,153 |
0,158 |
0,189 |
0,188 |
|
Базовые CHAID |
0,046 |
0,133 |
0,084 |
0,091 |
0,110 |
0,123 |
0,170 |
0,172 |
|
Алгоритмы Logistic |
0,376 |
0,440 |
0,037 |
0,050 |
0,072 |
0,077 |
0,149 |
0,150 |
|
NeuralNet |
0,051 |
0,122 |
0,155 |
0,156 |
0,126 |
0,129 |
0,206 |
0,205 |
|
KNN |
0,099 |
0,155 |
0,023 |
0,051 |
0,063 |
0,109 |
0,127 |
0,178 |
|
SVM |
0,024 |
0,066 |
0,002 |
0,009 |
0,076 |
0,079 |
0,135 |
0,152 |
|
Max |
0,376 |
0,440 |
0,006 |
0,017 |
0,063 |
0,074 |
0,128 |
0,138 |
|
Композиции Voting |
0,022 |
0,079 |
I 0,030 |
0,039 |
0,056 |
0,067 |
0,139 |
0,148 |
|
Monot |
0,002 |
0,099 |
0,000 |
0,014 |
0,022 |
0,064 |
0,099 |
0,143 |
Рис. 4. Средняя частота ошибок на обучающей и контрольной выборках для рассматриваемых задач, базовых алгоритмов и композиций. Жирным шрифтом выделен минимум значений в каждом столбце
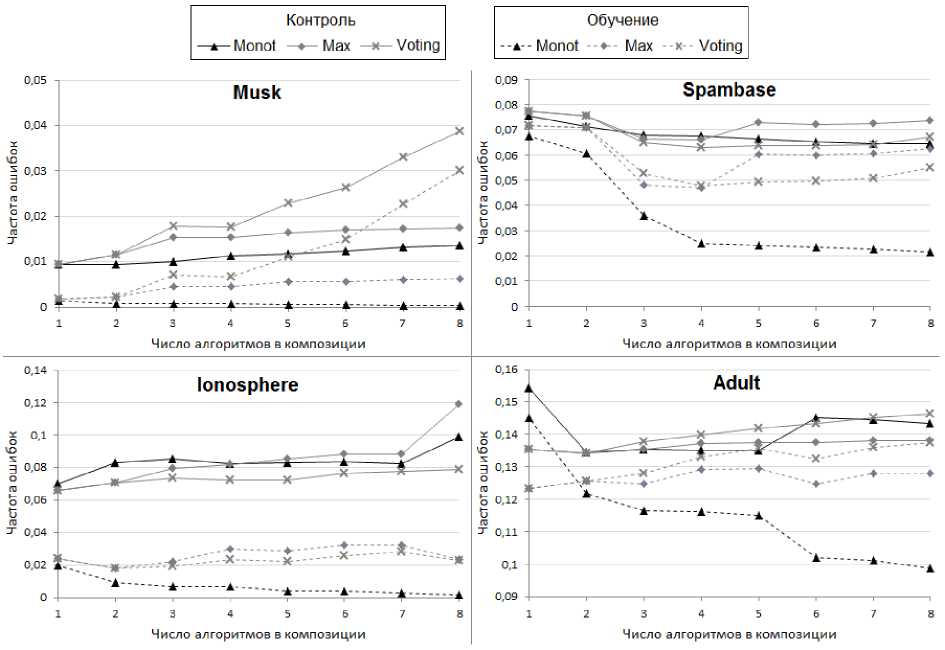
Рис. 5. Средняя частота ошибок на обучающей и контрольной выборке для рассматриваемых композиций в зависимости от числа наиболее качественных алгоритмов, входящих в их состав
Из рис. 4 видно, что для большинства задач качество классификации контрольной выборки некоторыми базовыми алгоритмами лучше, чем рассматриваемыми композициями, построенными над ними. Это связано с тем, что одни базовые алгоритмы существенно лучше решают конкретную задачу классификации, чем другие. Поэтому при построении композиций включение одних базовых алгоритмов добавляет новую информацию, помогающую повысить качество классификации всей композиции, тогда как включение других базовых алгоритмов лишь добавляет шум и снижает это качество.
Для устранения этого эффекта упорядочим все базовые алгоритмы по убыванию качества решения каждой задачи, то есть по возрастанию средней частоты ошибок на контрольной выборке. Будем последовательно включать базовые алгоритмы в соответствии с этим порядком в композиции и измерять их среднее качество на двух выборках, повторяя описанный выше эксперимент (рис. 5).
Анализ рис. 5 позволяет сделать вывод о сильной склонности монотонной композиции к переобучению, так как средняя частота ошибок на обучающей выборке для всех четырех задач достаточно быстро падает при добавлении каждого следующего алгоритма в отличие от средней частоты ошибок на контрольной выборке.
Также из рис. 5 видно, что для задач Musk и Ionosphere использовать рассматриваемые композиции не имеет смысла, поскольку добавление второго и всех последующих алгоритмов лишь ухудшает качество классификации. Действительно, для этих двух задач качество базового алгоритма SVM на контрольной выборке существенно превосходит качество всех остальных базовых алгоритмов на контрольной выборке (рис. 4). Поэтому остальные алгоритмы лишь добавляют шум, что приводит к ухудшению качества классификации. Этот эффект наиболее ярко выражен в задаче Ionosphere при добавлении восьмого базового алгоритма (логистическая регрессия) в монотонную композицию. Индивидуальное качество логистической регрессии на контрольной выборке в разы хуже, чем у остальных базовых алгоритмов, и ее добавление приводит к существенному падению качества всей композиции.
Для задачи Adult в случае построения монотонной композиции осмысленно использовать два базовых алгоритма (SVM и C50), хотя построенная композиция не дает существенного улучшения качества классификации по сравнению с одним базовым алгоритмом C50.
Для задачи Spambase в отличие от всех остальных использование всех восьми базовых алгоритмов приводит к наилучшему качеству классификации контрольной выборки монотонной композицией, причем это качество является наилучшим среди всех рассматриваемых алгоритмов (рис. 4).
Таким образом, построение монотонной композиции, используя независимо обученные базовые алгоритмы, может приводить к улучшению качества классификации как по сравнению с каждым из базовых алгоритмов, так и по сравнению с двумя другими рассматриваемыми в работе композициями. При этом если для некоторой задачи один базовый алгоритм решает задачу существенно лучше всех остальных, то построение монотонной композиции смысла не имеет, так как добавление остальных алгоритмов в композицию лишь вносит шум и приводит к переобучению.
Открытым остается вопрос о том, какими свойствами должен обладать очередной базовый алгоритм, чтобы при его добавлении в монотонную композицию повысить качество классификации контрольных данных.
Список литературы Минимизация эмпирического риска при построении монотонных композиций классификаторов
- Гуз И.С. Нелинейные монотонные композиции классификаторов//ММРО-13. -2007. -С. 111-114.
- Barlow R.E., Bartholomew D.J., Bremner J.M., Brunk H.D. Statistical inference under order restrictions; the theory and application of isotonic regression. New York: Wiley, 1972
- Воронцов К.В. Локальные базисы в алгебраическом подходе к проблеме распознавания: диссертация на соискание ученой степени к.ф.-м.н., М.: ВЦ РАН -1999.
- Hopcroft J.E., Karp R.M. An n 5/2 algorithm for maximum matchings in bipartite graphs, SIAM Journal on Computing 2 (4): 225-231
- Kхnig D. Gr afok es m atrixok. Matematikai es Fizikai Lapok 38: 116-119.
- Воронцов К.В. Комбинаторный подход к оценке качества обучаемых алгоритмов//Математические вопросы кибернетики. -2004. -№ 13. -С. 5-36.
- Quinlan R. 2011, http://rulequest.com/see5-win.html
- Breiman L., Friedman J.H., Olshen R.A., Stone C.J. Classification and regression trees. Monterey, CA: Wadsworth & Brooks/Cole Advanced Books & Software. 1984
- Loh W.-Y., Shih Y.-S. Split selection methods for classification trees, Statistica Sinica. -1997. -V. 7. -P. 815-840.
- Kass G.V. An Exploratory Technique for Investigating Large Quantities of Categorical Data. Applied Statistics. -V. 29, N 2. -1980. -P. 119-127.
- Fine T.L. Feedforward Neural Network Methodology, 3rd ed. -New York: Springer-Verlag. -1999.
- Cover T.M., Hart P.E. Nearest neighbor pattern classification. IEEE Transactions on Information Theory 13 (1): 21-27.
- Agresti A. Building and applying logistic regression models. An Introduction to Categorical Data Analysis. Hoboken, New Jersey: Wiley. P. 138.
- Cortes C., Vapnik V. Support-Vector Networks, Machine Learning, 20, 1995.
- Воронцов К.В. Оптимизационные методы линейной и монотонной коррекции в алгебраическом подходе к проблеме распознавания//ЖВМ и МФ. -2000. -Т. 40, № 1. -С. 166-176.
- Рудаков К.В., Воронцов К.В. О методах оптимизации и монотонной коррекции в алгебра-ическом подходе к проблеме распознавания. Доклады РАН. -1999. -Т. 367, № 3. -С. 314-317.
- Воронцов К.В. Комбинаторные обоснования обучаемых алгоритмов//ЖВМ и МФ. -2004. -Т. 44, № 11. -С. 2099-2112.
- Журавлёв Ю.И. Об алгебраическом подходе к решению задач распознавания или классификации//Проблемы кибернетики. -1978. -Т. 33. -С. 5-68.
- Freund Y., Schapire R.E. A decision-theoretic generalization of on-line learning and an application to boosting. European Conference on Computational Learning Theory. -1995. -P. 23-37


