Минимизация представлений логических функций в базисах Шеффера и Пирса

Результаты, полученные в математической логике, нашли широкое применение в конструировании электронных микросхем [1-3]. В частности, важной является задача представления произвольных логических функций с помощью формул, содержащих логические операции из заданного набора. Такие наборы операций называются функционально полными. Для того чтобы набор логических операций был функционально полным, необходимо и достаточно, чтобы он удовлетворял критерию Поста [1, 3]. Также рассматривается задача сокращения количества используемых операций заданного набора в логических формулах, связанная с задачей сокращения количества логических элементов в устройствах цифровой техники.

Наиболее изученными функциональными наборами логических операций являются стандартный базис (« л », « v », « — »), в котором логические функции представляются в виде конъюнктивных и дизъюнктивных нормальных форм, и базис Жегалкина (« © », « л », «1»), в котором логические функции единственным образом представляются полиномами Жегалкина [2].

Среди функционально полных наборов логических операций выделяются два набора, каждый из которых включает только одну операцию: базис Шеффера, включающий штрих Шеффера «|», и базис Пирса, включающий стрелку Пирса « Ф ». В связи с тем, что указанные наборы включают только по одной операции, логические формулы с их использованием, как правило, являются очень громоздкими.

В данной работе рассматривается вопрос сокращения количества операций в логических формулах в базисах Шеффера и Пирса.

Представление дизъюнктивных и конъюнктивных одночленов в базисах Шеффера и Пирса

Операция «штрих Шеффера» является комбинацией конъюнкции и отрицания, а операция «стрелка Пирса» - комбинацией дизъюнкции и отрицания. Поэтому традиционный подход к переходу к базисам Шеффера и Пирса заключается в использовании законов де Моргана и двойного отрицания.

Рассмотрим логическую функцию, заданную дизъюнктивным одночленом

X v ... v x n .                                           (1)

и приведём примеры её представления в базисе Шеффера для случаев n = 3 и n = 4.

• 1)    Пусть n = 3 . Тогда, используя законы де Моргана и двойного отрицания, получим:

X 1 v X 2 v X ₃ = X 1 л X 2 v X 3 = X 1 | X 2 v X 3 | X ₃ = X 1 | X 2 v X ₃ | X 3 = X 1 | X 2 л X ₃ | X ₃ = ( ( X 1 | X 2 ) | ( X 1 | X 2 ) ) |

| ( ( ^X 3 I ^X 3 ) I ( ^X 3 I ^X 3 ) ) .

Данная запись является громоздкой и содержит 7 логических операций.

Количество операций можно сократить, применив, например, закон Порецкого:

X1 л X2 V X3 = (X1 л X2 л X3 ) V X3 = (X1 л X2 л X3 ) V X3 = (X1 л X2 л X3 ) л x3•

Данная запись является более компактной по сравнению с предыдущей записью и включает только 3 логические операции.

• 2)    Пусть n = 4. Тогда, используя аналогичные рассуждения, получим:

XY V x2 V x3 V x4 = xY л x2 л x3 V x4 = xY л x2 л x3 V x4, применив закон Порецкого

(x л x2 л x3 л x4 ) V x4 = (x л x2 л x3 л x4 ) л x4 = (x л x2 л x3 | x4 ) | исходя из формулы для n = 3, получаем

(x л x2 л xз | x4 ) | x4 = ((((x | x2 ) | xз ) | xз ) | x4

- 4 •

Полученные результаты позволяют заметить рекурсивную зависимость при представлении одночлена (1) в базисе Шеффера.

Теорема 1. x v x ₂ v x ₃ v ... v x_n = ( ... ( ( ( ( X i | x^ ) | x ₃) | x ₃) |... ) | x „) | x „ •

Доказательство. Для доказательства воспользуемся методом математической индукции, учитывая явно прослеживающуюся в приведённых примерах рекурсивную зависимость.

Введем функцию y такую, что

• Y 1 = ^X 1 | ^X J Y 2 = ^X 1 | ^x 2 ; Y k = ( Y k - 1 | x k ) | x k , k >  2.

При n = 1 x = X j | X j = y ; при n = 2 x_Y л x ₂ = x | x ₂ = y₂ ; при n = 3

x л x2 V X- x3 = Y3•

Полученные зависимости используем как базу индукции. Далее предположим, что для n = m выполняется равенство

^X1 ^V x 2 ^V x 3 ^V ... ^V x m = ( ••• ( ( ( ( ^X 1 | ^X 2 ) | ^X 3 ) | ^X 3 ) k) | x m ) | ^Xm = Y m , докажем, что утверждение верно для n = m + 1:

^X 1 ^V x 2 ^V x 3 ^V ... ^V x m ^V x m + 1 = ^X 1 ^{л X} 2 ^{л X} 3 ^л - ^{л X}m ^{V X}m + 1 = ( ^X 1 ^{л X} 2 ^{л X} 3 ^л - ^{л X}m ^{л X}m + 1 ) ^{V X}m + 1 =

= ( ^X 1 ^{л X} 2 ^{л X} 3 ^л ... ^{л X}m ^{л X}m + 1 ) ^{л X}m + 1 = ( ^X 1 ^{л X} 2 ^{л X} 3 ^л - ^{л X}m | ^Xm + 1 ) | ^Xm + 1

) ^{1 X}m + 1 = Y m + 1 .

Использование данной теоремы позволяет уменьшить количество логических операций при переходе к базису Шеффера. К примеру, при «традиционном» переходе от дизъюнктивного одночлена к базису Шеффера (с использованием только закона де Моргана и двойного отрицания) для n = 3 и n = 4 количество логических операций равно 7, для n = 5 -16, а при применении теоремы 1 количество операций можно сократить до 3, 5, 7 соответственно.

Следствие. / f = ( ... ( ( ( ( f . | f 2 ) | f , ) | f , ) |... ) | f n ) | f n , где ^ - произвольная булева функция.

Математика

Следствия из теорем 1 и 2 используются при описании перехода от минимальной дизъюнктивной нормальной формы (МДНФ) и минимальной конъюнктивной нормальной формы (МКНФ) к базисам Шеффера и Пирса соответственно.

Алгоритм перехода от МДНФ и МКНФ к базисам Шеффера и Пирса

Вначале разработаем алгоритм перехода от МДНФ к базису Шеффера и по аналогии построим алгоритм для МКНФ. Основанием того, что переход осуществляется именно от МДНФ к базису Шеффера, является то, что запись, полученная в результате перехода, будет содержать меньшее количество логических операций.

Рассмотрим функцию n переменных

k f (xx,™, xn ) = vV<>

I = 1

n где Vi = A“tgt, at = t=i

0, если gt несодержитсяв v , gt - литерал (переменная или её отрицание).

Применяя следствие из теоремы 1, получаем

V1 a ... a Vk = ((...((( V1 IV2 ) IV3) | V3) |...) | v ) | v .

Для перевода V в базис Шеффера также воспользуемся теоремой 1. Введем обозначение:

V i = A « t g t = Y _Vl , t = 1

тогда с учетом обозначения получаем

(...(((V1 1V2)1V3)1 V3)k)1 Vk)1 Vk = ((...(((Yv1 1 Yv2 )1 Yv3 )1 Yv3 )h")1 Yv, )1 Yv,

Полученные выкладки положены в основу алгоритма перехода от МДНФ в базис Шеффера, представленный ниже.

Шаг 1. Рассматриваем Vi как переменные и осуществляем переход в базис Шеффера, но при этом сохраняем инверсию Vi•

f ( ^x 1 ,..., ^xn ) = ( (." ( ( ( V 1 ^| V 2 ) ^| V з ) ^| V 3 )h-) ^| V k ) ^| V k .

Шаг 2. Осуществляем преобразование V i,..., V применяя теорему 1. Если есть инверсия x , то преобразование осуществляется по формуле x = x | x .

Шаг 3. Записываем окончательный результат.

Замечание . Для уменьшения количества логических операций необходимо сдвинуть на первые места переменные x в конъюнктивном одночлене ( x_x a x₂ a x₃ a x ₄ = x₃ a x₄ a x_x a x ₂).

По аналогии получаем алгоритм для МКНФ с аналогичным замечанием.

Шаг 1. Рассматриваем v как переменные и осуществляем переход в базис Пирса, но при этом сохраняем инверсию Vi• f (x1,...,xn

V1 Ф V2 ) Ф V3) Ф V3) Ф...) Ф Vk)

^Ф V k

Шаг 2. Осуществляем преобразование V i,..., V , при помощи теоремы 2. Если есть инверсия x ,уто преобразование осуществляется по формуле x = x Ф x .

Шаг 3. Записываем окончательный результат.

Численный пример

Рассмотрим логическую функцию

Меньших В.В.,                              Минимизация представлений логических функций

Никитенко В.А.                                                 в базисах Шеффера и Пирса f (Xj, X2 , x3, x4 ) = (Xj A x2 A x4 ) V (Xj A X2 A X3 ) v( X, A X3 A X4 ) = (Xj A X2 A X4 ) V (Xj A X2 A X3 ) v( Xj A X4 A X3 )

^ = (X A X2 A X4 ), ^2 = (Xy A X2 A X3 ), ^3 = ( Xy A X4 A X3 ) .

Опишем результаты реализации алгоритма.

Шаг 1.

f ( Х^ X 2 , Х 3 , X 4 ) = ^ V ^ 2 V ^ ₃ = ^ V ^ V^V ^ = ^ A V 2 A^A ^ = ((^ | t^M) I ^ 3 .

Шаг 2.

^ ₁ = X 1 A х ₂ A х ₄ = (( х 1 1 х ₂) | х ₄) | х ₄; ^ 2 = ^X 1 ^A x 2 ^{A X} 3 = ( ( ^X 1 |^{( X} 2I ^X 2 ) ^{1 X} 3 ) ^{1 X} 3 ;

V 3 = X A X 4 A X 3 = ((( х 1 X 1 ) I ( x 4 1 x 4 ))! X 3 ) | X 3 ;

Шаг 3.

^f ( ^X , , x 2 , ^X 3 , ^X 4 ) = [ ⁽⁽ X I ^X ₂)| ^X 4 )1 ^X 4 ] I [ ⁽⁽ X I ^{( X} 2 I x2)) I X^ ^X 3 ] I [ ⁽⁽⁽ X I ^X 1 ) |^{( X} 4 I ^X 4 )) I ^X 3 )1 ^X 3 ] I

I [ ^{((( X} 1 ^{| X} 1 )|^{( X} 4| ^X 4 ^))| X^ ^X 3 ] •

Полученная функция в базисе Шеффера имеет 20 логических операций. Стоит заметить, если бы мы не последовали замечанию алгоритма, то функция имела бы 22 логические операции.

Замечание

Одним из недостатков перехода в рассматриваемые базисы является то, что, как правило, увеличивается количество логических операций. Однако следует отметить, что при переходе в данные базисы количество операций может и уменьшится. Примером может быть функция f (х,x2,x3) = (x1| x2)| x3.                                     (2)

При переходе в стандартный базис она будет иметь вид f (X, X2, X3 ) = (X a x2 )v x3 .                               (3)

Расчет количества логических операций в базисах Шеффера и Пирса

На основе анализа приведённых выше алгоритмов была получена зависимость для количества логических операций. Обозначим:

f ( Х з,•••, х _и) = Х з a х₂ a х₃ a ••• a x„ = f ⁿ - конъюнктивный одночлен;

f ( ^X 1 ,

• ••

. X . ) = f n - (-( ( ( < X , | X 2 ) | X 3 ) | X 3 ) |- ) | X , ) | X , - запись f . в базисе Шеффера (исполь

зуя теорему 1);

Х_п - количество операций «|» в f ” ;

к - количество конъюнктивных одночленов в формуле;

. - количество переменных в ^ .;

Г 1, если . = 1,

N_t = <                   - количество «|», возникающих при переходе от конъюнктивных

^ 2 . - 3, если . >  2, одночленов к базису Шеффера;

j_t <  . - количество инверсий переменных в ^ .;

'О, если ^j _t = 0,

I = з 1, если j = 1,      - количество «|», возникающих при переходе от инверсии к «|»;

2 j - 2, если j >  2,

G^Jj'’."• ^jk^k - количество «|» при переходе в базис Шеффера. . ] ,..., n k

Лемма 1. Пусть был осуществлен переход f . в f ” , тогда \ имеет вид:

f 1, если n = 1,

Л = З ,             ,

1 2 n - 3, если n >  2^

Математика

Доказательство. Для доказательства воспользуемся методом математической индукции. Ба- за индукции

При n = 1

%! = %! | %!, A = 1 .

При n = 2

%! V %2 = %! | %2, A = 1 = 2 • 2 - 3 .

При n = 3

%! V %2 V %3 = ((%! | %2 ) | %3 ) | %3 , A = 3 = 2 • 3 — 3 .

Предположим, что для n = m выполняется равенство

%1 V %2 V %3 V ... V %т =(...((((%1 | %2 ) | %3 ) | %3 ) |...) | %m ) | %m , Am = 2m - 3 , докажем, что выполняется для n = т +1, имеем равенство

% 1 ^V % 2 ^V % 3 ^V ... ^V % m ^V % m + 1 = ( ( ( ... ( ( ( ( % 1 । % 2 ) | % 3 ) | % 3 ) |- ) | % m ) | % m ) | % m + 1 ) | % m + 1 •          ⁽⁴⁾

Количество операций для функции f ^{m + 1} получается путем прибавления к A двух логических операций, как видно из равенства (4). Тогда имеем рекуррентное соотношение A _m + i = A _m + 2 . По предположению индукции, что A _m = 2 m - 3, получаем A _{m + 1} = A _m + 2 = 2 m - 3 + 2

= 2 m + 2 - 3 = 2( m +1)-3 = A+!•■

Лемма 2. Поставим в соответствие каждому %, из выражения f n литерал g_t. Пусть количество литерал, которые являются инверсией %,, равно n ' , тогда количество логических операций «|» при переходе от инверсии к «|» A' имеет вид:

0, если n ' = 0,

A n - =1

1, если n ' = 1, 2 n '- 2, если n '> 2.

Доказательство. По аналогии с леммой 1 воспользуемся методом математической индукции для доказательства. Для случая n' = 0 очевидно, что a = 0 • База индукции n' = 1. Рассмотрим fn вида g1 Л g2 Л ... Л %Л ... Л gn .

Так как количество литералов, которые являются инверсией x , равно 1, то согласно замечанию переместим его на первое место, в силу коммутативности операции « л »

% ^Л g 2 ^Л ... ^Л g 1 ^Л ... ^Л g n .

При переходе к базису Шеффера получаем

( ( ... ( % | g 2 ) |- ) | g n ) | g n = ( (-( ( %i | % i ) | g 2 ) к. ) | g n ) | g n ^ М 1 = ¹ .

• n ' = 2. По аналогии с шагом для n ' = 1 рассмотрим f n с двумя инверсиями %, и % без ограничения общности i <  3 ₂, получаем

% i 1 ^Л % 3 ₂ ^Л ... ^Л g n = ( ( ... ( % i 1 | % i ₂ ) | ... ) | g n ) | g n = ( ( ••• ( ( % i 1 | % i 1 ) | ( % i ₂ | % i ₂ ) ) | ... ) | g n ) | g n ^ М 2 = ² = ² • ² - ² .

n ' = ³ , %Ц , % /₂ , % /₃ , ⁱ1 <  ⁱ 2 <  3₃

% 1 ^Л % i ₂ ^Л % i ₃ ^Л ... ^Л g n = ( ( ... ( ( % i 1 | % 2 ₂ ) | % i ₃ ) | % i ₃ ... ) | g n ) | g n =

= ( ( ... ( ( ( % i 1 । % i 1 ) । ( % i ₂ । % i ₂ ) ) । ( % i ₃ । % i ₃ ) ) । ( % з ₃ | % i ₃ ) ... ) | g n ) | g n

^ М3 = 4 = 2 • 3 - 2.

Предположим, что для n = m выполняется равенство

X: л x_i л x_i Л ... Л X,- л ... л g„ = i ₁        i ₂        i ₃               i_m               n

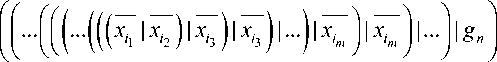
I g n =

( ( ■■■ ( ( ( ( ^X 1 ¹ X ) ¹ ( ^x 2 ^{1 x} 2 ) ) ¹ ( ^x 3 ^{1 x} 3 3 ) ) ¹ ( ^x 3 ^{1 x} 3 ) ) ¹... ) ¹ ( ^x m ¹ x m ) ) ¹ ( ^x m ^{1 x} m ) } ¹... j ¹ g n J ¹ g n =

^ ^ _m = 2 • m - 2.

Докажем, что выполняется для n = m +1. Имеем равенство xi1 Лx2 лx33 л...лxm+1 л...л gn =

=    "•^^( (" • ( ( ( ( x 1 ¹ x i 1 ) ¹ ( ^x2 ^{1 x}2 ) ) ¹ ( x i 3 ^{1 x}3 ) ) ¹ ( x i 3 ¹ x e ) ) ¹... ) ^{1                         (5)}

| x | x | x | x | x | x          | ... | g | g .

¹ \  ¹ m ' m ))'\  ¹ m ^{1  1} m )) ' \  mi +1 ¹   im +1 / у ¹ n \ on n\on

Количество операций для функции fm+1 получается путем прибавления к ^ двух логических операций, как видно из равенства (5). Тогда имеем рекуррентное соотношение ^+х = ^ + 2. По предположению индукции, что   ^m = 2 m - 2, получаем   ^m+1 = ^m + 2 = 2 m - 2 + 2 =

= 2 m + 2 - 2 = 2 ( m + 1 ) - 2 = ^ _+P^

Теорема 3.

• 1.    Если k = 2, то

• 2.    Если k >  3, то

Gnjn = S(Ii + N) +1 ■(6)

2 k

Gj™j = Z(I + N) + 2L(I + N) + 2* - 3 .(7)

• i=1

Доказательство.

• 1.    Рассмотрим конъюнктивный одночлен вида

• 3.    Рассмотрим конъюнктивный одночлен вида

(g1 л ... л    )V( g12 л ...л gl22 ) , при переходе к базису Шеффера получаем f   ((g,1 । g 1 ) |-) । g 1 g,1 J । f   ((g2 । g2 ) |-) । g2    g2 j .                              (8)

Ц    V l ^l1 '    )    ln / S J Ц   W l 1 ^l1 ’    ) ^ln 2 / ^ln 2 )

Согласно лемме 1 в каждой скобке выражения (8) логических операций будет 2 n - 3 и 2 n ₂ - 3 (если n , n ₂ >  2, иначе одна логическая операция), что соответствует обозначению

N , N . Если количество литералов в каждой скобке выражения (8), являющихся инверсией переменных, равно n ', n ‘ , то согласно лемме 2 их численное значение имеет вид I_n ‘ , I_п._г соответственно. Также добавляется еще одна логическая операция « | », стоящая между скобами, выражения (8).

I g 1 ^л ... ^л g ,1   |^V| g_[ 2 ^л ... ^л g, 2   |^V ... ^V| g * ^л ... ^л g *  I                               ⁽⁹⁾

V 1             n1 J V 1             n 2 J         v 1             n* J при переходе к базису Шеффера получаем

( ( ... ( ^g i 11 | ^g i\ ) | ■■■ ) | ^g i n ) | ( ( ■■■ ( ^g i2 | ^g i 1²

) |... ) ¹ g^ ) ¹ ( ( ... ( ^g i 3 ^{1 g} i 1³

) ¹ ... ) ^{1 g} l n ₃ ) ¹ ... ¹ ( ( ■■■ ( ^g l 1 * ^{1 g} l 1 *

)^ .. ) | g l n* ) .⁽¹⁰⁾

Разобьем пункт 2 теоремы 3 на 3 части. Докажем, что: 2

1') ^ ( I + N ) выполнятся для 1-й и 2-й скобки;

i = 1

Математика

k

2') 2 ^ ( It + N ) выполнятся для скобок 3,..., к ; i = 3

3') 2 к - 3 дополнительное слагаемое.

1') Смотрите доказательство пункта 1 теоремы 3.

2') Скобки 3,..., k

порождают ( 1 ^ + ... + I_{n t}) + ( N „₃ + ... + N _t) , как было показано в пункте 1

доказательства теоремы 3. Когда количество конъюнктивных одночленов к > 3, то каждая скобка, начиная с 3-й повторяется 2 раза, следовательно, количество логических операций« | » удваи- вается 2 -TfI  +... +1 1 + (N +... + N 11.

L\ ⁿ 3            nk /   \   n 3              nk /J

3') Обозначим ^ g _v л ... л g_v J = ^ , тогда выражение (9) будет иметь вид

CTj V СТ2 V ... V ст3, переходя к базису Шеффера получаем

(™ ( ( ( ( ° i I ^ 2 ) I ^ 3 ) I ^ 3 ) |... ) I ° к ) I ^ к , где количество символов согласно лемме 1 равно 2 к - 3 . ■

Полученные формулы (6) и (7) справедливы при выполнении замечания алгоритма. Однако предложенная формула не срабатывает при малом количестве переменных в дизъюнктивных одночленах. Примером может служить случай, который рассматривался в начале раздела (2), (3). Применяя формулу, получаем G 0,1 = 4, хотя логических операций всего 2. Аналогичная формула и для перехода к базису Пирса.

Заключение

При осуществлении перехода от стандартного базиса к базисам Шеффера и Пирса «традиционным» образом количество операций возрастает нелинейно. Анализ полученных формул для количества логических операций G показывает, что в случае использования предложенных алгоритмов количество логических операций, а в свою очередь и количество логических элементов в устройствах цифровой техники, будет увеличиваться линейно в зависимости от количества переменных подаваемых на вход микросхемы, что определяет практическую ценность полученных результатов.