Mining Associated Factors about Emotional Disease Bases on FP-Tree Growing Algorithm

Published Online August 2011 in MECS

Available online at

• 1.    Introduction

• 2.    The Representation of FP-Tree

With the increasing of social competition and work pressure, diseases caused by emotion become more and more, and the influence on health and disease exerted by emotional abnormity becomes increasingly seriously, which have aroused great social attention[1,2]. To study the main reason and rule of Emotional Disease, herbalist doctors apply questionnaire in general psychology condition, evaluation of mood ,study of Chinese medicine diseases and evaluation of curative effect, setting anger and anger-in life events questionnaire, Eysenck Personality Questionnaire (EPQ), State Trait Anger expression Inquiry (STAXI) Scale, Trait Coping Style Questionnair (TCSQ), Perceived Social Support Scale (PSSS)[3], anger and anger-in predisposition * Corresponding author.

questionnaire, anger and anger-in Physiological State Questionnaire(PSQ) [3] and a number of test indicator data. To reveal the pathogenesis which induces Emotional Disease, and look for effective interventional way, the DBMS of Emotional Disease should be built[4], providing experimental data for study of epidemiology, clinical retrospective research and prospective study, and then excavating associating factors associated with disease from a large amount of collected data. This is the purpose of study in this paper.

To excavate factors associated with Emotional Disease, we should firstly find out the itemsets that satisfy pathogenic condition, and then find out the itemsets that met minimum support. Accordingly, the key issue of this paper is to finding out related frequent itemsets in a large data sets at high efficiency. The main problem of classical excavation bases on FP-Tree frequent itemsets is the high cost of I/O caused by repeated scan, and the later studies put forward a lot of methods that can reduce the scanning times of database [5]. Recently, the method that reducing the scanning of database through decreasing the search space of itemsets has been widely studied. For instance, the classic representation is the FP-Tree growth algorithm putted forward by Han [6], which scans information through records of state tree rather than use candidate frequent itemsets, thus building frequent itemsets through scanning database for only one time. This paper applies this algorithm to the database of emotional disease, building the final largest frequent itemsets step by step through one time scanning, and then listing pathogenic associated factors.

FP-Tree is a kind of compressed representation of the input data, it’s constructed by reading transaction one by one and mapping each transaction to path of FP-Tree. Because different transactions may have several kinds of the same items, their path may overlap. The more the path overlapping, the better the compressed results that got by FP-Tree structure will be. If a FP-Tree is small enough to stored in the memory, you can directly extract frequent itemsets from this in-memory structure, without repeatedly scanning data in the hard disk. Every items in the emotional questionnaires have many parts, such as when you encounter difficulties or unpleasant in the daily life, how would you treat it? We choose five kinds of grade which from 5 to 1 that represent answer from "affirmation is" to "affirmation isn't", that is "Certainly is" choose 5 and "surely not" choose 1. In so way, each items in transaction has five values, Ti_1, Ti_2, Ti_3, Ti_4 and Ti_5. Table 1 shows a transaction database table, it contains 10 transaction and five items, suppose minimum support is 30%,the frequent items, namely {t1_5},{t2_2},{t2_4},{t2_5}, {t3_3},{t3_4},{t4_1},{t4_4},{t5_4},{t5_5} that the least counting is less than three are non-frequent item. According to the support degree's degressive sort, the frequent items's dataset are shown as Table 2.

Table 1. Transaction Database Table

TID	t1	t2	t3	t4	t5
1	2	3	1	2	4
2	2	3	1	2	3
3	3	2	3	4	2
4	3	4	2	3	2
5	2	3	2	4	3
6	3	4	2	3	2
7	3	3	2	3	3
8	5	3	4	1	5
9	2	3	1	2	4
10	3	5	2	3	2

Table 2 Transaction Dataset Table

TID	Item
1 2 3 4 5 6 7 8 9 10	{t2_3,t1_2,t3_1,t4_2} {t2_3,t1_2,t3_1,t5_3,t4_2} { t1_3,t5_2} {t1_3,t3_2,t5_2,t4_3} {t2_3,t1_2,t3_2,t5_3} {t1_3,t3_2,t5_2,t4_3} {t2_3,t1_3,t3_2,t4_3,t5_3} {t2_3} {t2_3,t1_2,t3_1,t4_2} {t1_3,t3_2,t5_2,t4_3}

To facilitate the algorithm's top-down search, every node in the FP-tree that the algorithm has used will at least composed by five fields [7]: "node-name", "node-count", "node-link", "node-child" and "node-parent". "node-count" counts the number of transaction which mapped to a given path. "node-child" points the child of the node. Because there may be many children, "child node" will be able to expand. The basic node fields are as follows:

node—name

node—count

node—link

node—child

node-parent

At first, the FP-Tree only contains a root node which marked with a symbol Null. Then, expand the FP-Tree with the following methods:

• (1)    Scan dataset one times and determine support counting of each items. The support degree is an important measure, because the rules with lower support degree is not convincing and it just happened accidentally. Support degree is often used to delete those uninteresting associated factors. Suppose the minimum support degree is 30%, items that support are less than three are non-frequent items. Sort the frequent item according to the support degree descending order. For datasets in table 2, t2_3's support degree counting is six, it's is the most frequent item. The next is t1_3:5; t3_2:5 and t1_2:4 respectively. Items that the support degree is more than three are frequent items;

• (2)    The algorithm will construct a FP-Tree at the second time's scanning. After read the first transaction, namely {t2_3,t1_2,t3_1,t4_2}, it will create nodes that tag with t2_3, t1_2, t3_1 and t4_2 and then it will form a path: Null→t2_3→t1_2→t3_1→t4_2, all nodes of this path’s frequency counting is one.

• (3)    The second transaction, {t2_3,t1_2,t3_1,t5_3,t4_2}, will share the same prefix item with the first one, the path of the second transaction and the first one will be partly overlap, so the frequent counting of nodes: t2_3,t1_2 and t3_1 can be increased to two, while the newly created node t5_3 and t4_2’s frequent counting equal to 1;

• (4)    After the algorithm read the third transaction, { t1_3,t5_2}, it will create new node set for items t1_3 and t5_2 which connect Null and form a path representing the transaction. Frequent counting of each node in this path will be equal to one.

• (5)    Continue the process until each transaction is mapped to a path in the FP-Tree.

After read all the transactions, the FP-Tree will be shown as Fig 1.

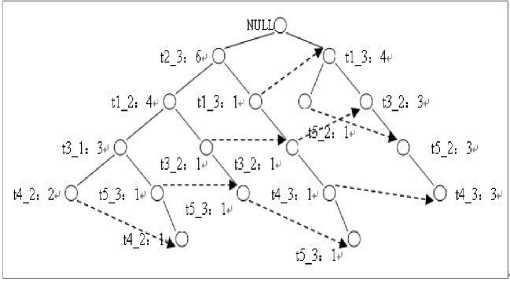
Fig 1. A complete FP-Tree

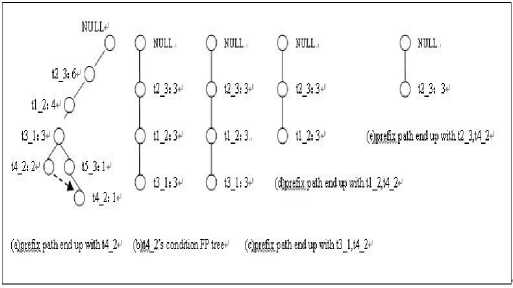
Fig 2. The process of FP-growth finding frequent itemsets

The algorithm of structuring FP-Tree is as following:

• (1)    Scan the transaction database, collect the frequent sets and the corresponding supporting degree, discard non-frequent items, and make a frequent item table L.

• (2)    Put all transactions into the array of the memory and obtain a transaction set List.

• (3)    Scan the frequent item table L and arrange the frequent items in the frequent item table by descending order through the bubble sort algorithm.

• (4)    Scan the transaction sets of the memory, discard the first transaction in the non-frequent item by comparing with the frequent item table L which has been arranged in order, then arrange the frequent items of the first transaction according to the supporting degree count by descending order.

• (5)    Firstly, create root node of the FP-Tree which is remarked by NULL, then read the first transaction sequenced, set the item table of the transaction as [ p | P ], in which p is the first frequent item, P is the frequent items that is derived. Call the procedure createTree ([ p | P ], _topNode , L ), in which _topNode is the current root node, L is the frequent item table. If _topNode has child node which makes N.ItemName equal to p.ItemName , N 's support degree count is added by 1, or else create a new node N, and set its support degree count as 1, connect it to its parent node _topNode , and connect it to the nodes which have the same ItemName through NextNode . Finally, delete the first frequent item from the first transaction , reduce the indexs of the rest of the frequent items by 1 at the same time, then obtain a new transaction item table [ p1 | P ], set the _topTreeNode as p . If the frequent item of the first transaction is non-null, recursively call the procedure createTree, each new _topTreeNode is the frequent item which was deleted last time until the first transaction is completely read.

• (6)    Now back to step 4, scan the transaction sets in the memory, filter and sort the second transaction, and then do the step (5), loop around the steps until the last transaction is processed, a complete FP-Tree is formed in the end.

• 3.    The MINING Frequent Itemsets

In general, the size of FP-Tree is smaller than the uncompressed data, because the transactions of the data table often share some common items. In the best case, all transactions have the same item sets, FP-Tree contains only one node path. When each item has a unique item set, the worst thing happens. As the transaction contains none of the common item, the size of FP-Tree is actually the same as the original data, however, the additional space is used for stored pointers and count for the nodes, the demand of FP-Tree storage is greater.

The FP-growth algorithm seeks tree from bottom to up, generate frequent itemsets via FP-tree. As the tree shown in Fig 1, firstly algorithm seeks the itemsets end up with t4_2, then t5_3, t3_1, t1_2 in turn, the last node is t2_3. Detailed states are as follow:

• (1)    Collect all paths that include node t4_2, these paths called prefix path, as shown in Fig 2 (a).

• (2)    The support degree count of node t4_2 is three, so {t4_2} is frequent itemset, then considering itemsets end up with {t4_2,t3_1},{t4_2,t1_2},{t4_2,t2_3} and {t4_2}. Transform prefix path into condition FP-Tree. Update the support count of prefix path, delete node t4_2, clip prefix path. After updating the support count of prefix path, some item may no longer be frequent item. As the support count of node t5_3 is 1, so itemset ends up with {t5_3, t4_2} is not frequent and delete node t5_3. It is shown as Fig 2 (b).

(3)In order to find frequent itemsets end up with t3_1 and t4_2, collect t3_1's prefix path from t4_2's condition FP-Tree. The support count of {t3_1, t4_2} is three, so it is frequent itemsets. Because this condition FP-Tree contains item t1_2 and t2_3 which support count equal minimum support degree, so algorithm picks up frequent itemsets {t1_2, t3_1, t4_2}, {t2_3, t3_1, t4_2} ,{t2_3, t1_2, t3_1, t4_2} and the result is shown as Fig 2(c).

• (4)    Find out frequent itemsets that end up with t1_2, t4_2. After handling t1_2's prefix path, find out that itemsets {t1_2, t4_2} is frequent. Because this condition FP-Tree contains an item t2_3 which support count equals minimum support degree, so algorithm picks up frequent itemsets {t2_3, t1_2, t4_2} and the result is shown as Fig 2(d).

• (5)    Finally, find out itemsets end up with t2_3, t4_2, and the result is that {t2_3, t4_2} is the only rest of frequent itemset which is shown as Fig 2 (e).

All frequent itemsets are shown in table 3.

Table3 Frequent itemsets in term of postfix sort

postfix	Frequent itemsets
t4_2	{t4_2},{t3_1,t4_2},{t1_2,t3_1,t4_2},{t2_3,t1_2,t3_1,t4_2},{t2_3,t3_1,t4_2},{t 1_2,t4_2},{t2_3,t1_2,t4_2},{t2_3,t4_2}
t5_3	{t5_3},{t2_3,t5_3}
t3_1	{t3_1},{t1_2,t3_1},{t2_3,t1_2,t3_1},{t2_3,t3_1}
t4_3	{t4_3},{t5_2,t4_3},{t3_2,t5_2,t4_3},{t1_3,t5_2,t4_3},{t3_2,t4_3},{t1_3,t3_2,t 4_3},{t1_3,t4_3},{t3_2,t5_2,t1_3,t4_3}
t5_2	{t5_2},{t3_2,t5_2},{t1_3,t5_2}, {t3_2,t1_3,t5_2}
t1_2	{t1_2},{t2_3,t1_2}
t3_2	{t3_2},{t1_3,t3_2}

The algorithm of mining frequent itemsets is described as follow:

Procedure FP-growth ( Tree , α )[8]

{ If FP-tree contains single path then:

• (1)    Firstly, get all node _treeNodeItemList in this path, figure out combination count N in this path. Secondly, get support count of every combination β in turns. The support count of β equals the minimum node support among β. At the same time, add this combination into combination aggregation _itemList . Do as this, support count of all combination and combination aggregation can be derived.

• (2)    Generate mode β∩α for every combination in single path.

Else

• (1)    Traverse all frequent items αi according to the support degree in ascending order. For every frequent item, generate a mode e=ai U a and its support degree is ai.

• (2)    Construct β's condition mode, add store their support count into several list in ascending order.

• (3)    Construct β's condition FP-Tree which is named as Treeβ .

• (4)    If Tree β is not null, call recursively FP-growth (Treeβ, β).  }

• 4.    The experiment of ming associated factors

• 5.    Conclusion

The experiment of research in this paper takes the datum of sleep quality survey as example. The score of sleep quality is stored in variable PSQI which includes seven ingredients. Ingredient I is the score of subjective sleep quality. If the sleep quality is very good, records 0 score; is better, record 1 score; is worse, records 2 scores; is worst, records 3 scores. Ingredient II figures out scores based on the ramp duration and degrees of sleeping difficulty. If the ramp duration is 15 minutes or less, marks as 0; is between 16 and 30 minutes, marks as 1; is more than 31 but less than 60 minutes, marks as 2, is more than 60 minutes, marks as 3. If there is no sleeping difficulty , scores 0; sleeping difficulty is less than one time a week, scores 1; is one or two times a week, scores 2; is more than 3 times a week, scores 3. Ingredientlll records on the sleeping time. If sleeping time is more than 7 hours, marks as 0; is between 6 and 7 hours, marks as 1; is only 5 to 6 hours, marks as 2, is less than 5 hours, marks as 3. Ingredient W marks routine sleep efficiency. Routine sleep efficiency equals to sleeping hours divide hours passed on bed and then multiply 100%. If sleep efficiency is more than 85%, records 0 points; is between 75% to 84%, records 1 points; is between 65% to 74%, records 2 points; is below 65%, records 3 points. Ingredient Vrecords on worry frequency which affects sleep. If there is no worry, marks as 0. If worry frequency is 1 to 9, marks as 1; is 10 to 18, marks as 2; is 19 to 27, marks as 3. Ingredient VI make scores according to the consumption of hypnotic drug. Without hypnotic drug records 0. If uses once or less a week, records 1; uses once to twice a week, records 2; users more than three times a week, records 3. Ingredient^ points by daily functions during a week. If no tiredness, marks 0. If feels tired no more than once a week, marks 1; once to twice a week, marks 2; more than 3 times during a week, marks 3. Once feels energy shortage, records 0; occasionally feels insufficient, records 1; sometimes be short of vitality, records 2 ; frequently feels deficient in energy, records 3. Ingredient^ sums of the two items. If the point is 0, marks 0; is between 1 and 2, marks 1; is 3 to 4, marks 2; is among 5 to 6, marks 3.

The total scores of PSQI sums up of Ingredient I , II ,Ш,W, V,V,^. The associated factors about sleeping quality are searched from Ingredient I , II , Ш, W, V , V and ^ according to total scores of PSQI. The experiment, which is based on more than 3000 records of sleep quality survey table, is to find the associated factors that affecting sleeping quality. The result shows that the most frequent associated factors which influence sleeping quality is breath impeded, cough or high snoring sound, feeling cold, feeling hot or the nightmare. Program analysis takes 2 seconds wholly.

It is important to develop the research of pathogenesis which tempt emotional disease, establish a scientific data management method, and mine main pathogenic factor for establishing different interventions way, adjusting human relationship which is important for the harmony of social, resolving kinds of conflict caused by anger, and improving the level of curing and preventing disease. Finding max frequent itemsets is one of key problem of data mining, and also a hot point of research. Because the data size of emotional disease's survey table is huge, and the classic frequent itemsets mining algorithm Apriori need to scan database several time repeatedly, the cost of I/O will be too high so that no valuable data is derived. This research adopts FP-tree algorithm, which is based on frequent mode tree, and provide a better platform of data analysis and mining. It has been applied to reality, and get the expected effects.

Acknowledgment

Acknowledgment the academic inherit and innovative research of symptomatic mechanism of Traditional Chinese Medicine. ( No. 2006CB504804 Developing plan of 973 basic research of national keystone ) .