Mining Sequential Patterns from mFUSP - Tree

Published Online June 2015 in MECS

Data mining (sometimes called data or knowledge discovery) is the process of examining data to distill useful information and helpful knowledge from large databases. This information may assist us to reach a determination. Mining useful information and helpful knowledge from large databases has evolved into an important research field in data mining arena. Among them, sequential pattern mining in large transactional databases plays an important part in this area. Sequential pattern mining is the procedure of obtaining the complete set of frequent occurring ordered events or subsequences from a set of sequences or sequence database. The advantage to find the sequential patterns is, we can see the customer's sequences and predict the probability to purchase some items in next transactions by the clients. For instance, if a customer bought egg and sugar in one transaction, then, we can predict the probability to buy milk by this customer in the next: that is, if {egg, sugar} then {milk}. It is widely applied in the analysis of customer purchase patterns or web access patterns, sequencing or time-related processes such as science experiments, natural disasters, and in DNA sequences, and so on. Agrawal and Srikant first introduced sequential pattern mining in 1995 [1]. Based on their study, sequential pattern mining is stated as follows: “Given a sequence database or a set of sequences where each sequence is an ordered list events or elements and each event or element is a set of items, and given a userspecific minimum support threshold or min_sup, sequential pattern mining is the process of finding the complete set of frequent subsequences, that is, the subsequences whose occurrence frequency in the set of sequences or sequence databases is greater than or equal to min_sup.” Past studies developed two major classes of sequential pattern mining methods; one class proposed apriori based mining algorithms and another class proposed pattern growth based mining methods. GSP (Generalized Sequential Pattern) [2] is an apriori based algorithm which can determine the complete set of frequent sequential patterns by using point-wise candidate sequences generation and test access. This algorithm scans the whole sequence database multiple times to find out the support count or frequency of each pattern from the database. As a result of multiple scanning, the complexity of GSP algorithm gradually increases with large database. PrefixSpan [3] is a pattern growth based approach which is similar to FP-growth [4]. It does not make a great number of useless candidate sets that makes out apriori based method. But, to see the sequential patterns, PrefixSpan recursively creates a circle of small projected databases from large databases. To do this, the algorithm first scans the original database to get the frequent items and their corresponding counts, and then, it starts the mining operation. In mining process, it first finds the subsequences for every prefix i.e. frequent items. After this, the algorithm finds the sequential patterns from the projected databases which are produced from each prefix sequence and then, it recursively creates set of small projected databases for every frequent subsequence. In this approach, the sequences grow from short to large with recursively projected databases which increases both the time and space complexity. Also, each time it commands to scan the projected database to find the frequent items that mean it needs multiple scanning of the projected database. Mining algorithm [5] of FUSP - tree [6] is also based on pattern growth approach which can find frequent sequential patterns from FUSP - tree data structure by recursively breeding set of small projected trees from the large tree. Links stored in the FUSP - tree facilitate to find the frequent items easily without scanning each projected tree, but each time it needs to expense lots of effort to update the links of each projected tree during mining.

Table 1. Sequence Database

Sequence ID(SID)	Sequence
10	p(pqr)(pr)
20	(pt)r(pu)
30	p(pqr)(pv)
40	(pq)(pt)

In this paper, we have developed a modified fast updated sequential pattern tree (called a mFUSP - tree) structure and mFUSP - tree mining algorithm based on pattern growth approach for sequence database. At first, this paper generates a mFUSP - tree structure of the sequence database to store only frequent items. For this ground, the large database is condensed into a smaller tree data structure and when frequent items are not exchanged, the approach doesn’t need to re- skim the original database once the tree is created and can get the results only from the tree. At the time of tree creation, it lays the frequency of each item in the tree’s node which helps us to dilute the effort of monotonous support counting during mining. In this way, our mining algorithm can overlook the multiple scanning of large database. It requires only twice scans of large database to create the mFUSP - tree. Our proposed mFUSP - tree mining algorithm is also capable to discover the complete set of frequent sequential patterns from the mFUSP - tree without re-building the intermediate projected trees. So that, our mining method can keep off the effort of links updating of each projected tree and our mFUSP - tree structure does not associate the same item in the tree; these are different from FUSP - tree [6]. In this study, we have provided both theoretical and substantial proof of the completeness and correctness of the mFUSP - tree mining algorithm. Moreover, a thorough experimental study is provided to compare the proposed approach with GSP [2], PrefixSpan [3], and FUSP-Tree Based mining [5] on both synthetic and real datasets. The results show that the proposed algorithm is much efficient than others.

The arrangement of this paper is as follows. Section 2 introduces the definitions of sequential pattern mining. In Section 3, we briefly review the pattern growth mining and two existing works. Section 4 proposes a compact data structure, called mFUSP - tree, for storing complete sequence database and a mFUSP - tree mining method with example for mining sequential patterns. Carrying out analysis is presented in part 5 and final section 6 draws the conclusion that points out the potency of our study.

• II.    Problem Definitions

Permit, I = {i1, i2, . . ., in} be a set of items in the database D.

Definition 1: A finite number of items, denoted as X = {i 1 , i 2 , . . ., i m }, for all 1≤ m ≤ n, is called an itemset or element or event. An itemset is also known as a subset of I or X occur in I, de-noted as X ⊆ I.

For example, let, I = {p, q, r, t} and (pqr) is an itemset or element or event of I where each item in (pqr) must exist in I.

Definition 2: A sequence is an ordered list of itemsets. A sequence s = (s 1 , s 2 , . . . , s m ) where s i is an itemset or element or event. An item can pass at most once in an ingredient of a sequence, but can occur multiple times in different ingredients of a sequence

For instance, s = {(p) (pqr) (prt)} is a sequence which has three elements or itemsets: (p), (pqr), (prt) and 4 items: {p, q, r, t}. Items p and r appear more than once in different elements but appear only once in separate element.

Definition 3: A sequence database D is a set of records or rows where each record represented as . SID (sequence ID) is the identifier of each sequence and s is the sequence. Table 1 shows a sequence database which contains four sequences and six items which are: {p, q, r, t, u, and v}.

Definition 4: The number of items in a sequence is called the length of the sequence. A sequence with length l is called an l-sequence.

For illustration, first sequence, s 1 = {(p) (pqr) (pr)} shown in Table 1 has 6 items. So, it is called 6-sequence.

Definition 5: The absolute support of a sequence s in a sequence database, D is the number of sequences in D that contain s. The relative support of a sequence s in a sequence database, D is the percentage of sequences in D that contain s.

For case in point, sequence (pq) appears 3 times in the Table 1, so the absolute support of (pq) is 3 and the relative support of (pq) is 75% {(100 × 3) ÷ 4}.

Definition 6: Given a minimum support threshold (min_sup), a sequence s is called a frequent sequential pattern in D if absolute support or support of s ≥ min_sup.

Let, the minimum support threshold is 50%. Specify that, for four sequences in Table 1, the minimum support threshold (min_sup) is (4*0.5) = 2. So, sequence (pq) is a frequent sequential pattern in Table 1 because the support of (pq) ≥ min_sup (3 ≥ 2).

Definition 7: For two sequences α = (α 1 , α 2 , . . . , α n ) and β = (β 1 , β 2 , . . . , β m ) where α i and β j are itemsets for 1 ≤ i ≤ n and 1 ≤ j ≤ m. β is defined as a subsequence of α if β 1 ⊆ α 1 , β 2 ⊆ α 2 , . . . , β m ⊆ α n .

Suppose s a = {(p) (pq)}. s a is a subsequence of s 1 and s 1 is a supersequence of s a . s a is sequential pattern of length 3 (i.e. 3-pattern).

Definition 8: For an item α from itemset I and a sequence s, the α-prefix of s is the prefix of s from the first point (the leftmost item) to the first occurrence of α inclusive and after the α-prefix is taken away, the remainder portion of s is known as the α-projection of s.

For exemplar, the q-prefix of the sequence {(p) (pqr) (pr)} is {(p) (pq)} and the q-projection is {(r) (pr)}.

Definition 9: If α is the last item of s then α-prefix is s itself and the α-projection is the empty sequence €.

For instance, the u-projection of {(pt) (r) (pu)} is € and u-prefix is this sequence itself.

Definition 10: The multiple set of α-projections from the sequences where α occurs in sequence database D is called the α-projection database D_α.

For example, all the q-projections from sequence database shown in Table 1 are {(r) (pr)}, {(r) (pv)}, and {(pt)}. These three sequences are known as q-projection database, Dq.

Definition 11: Sequence relation denoted as s-relation is a relation that exists between two items α and β if they appear in different itemsets of a sequence, s and itemset relation denoted as i-relation is a relation that exists between two items α and β if both appear in the same itemset of a sequence, s.

From Table 1, we can see that first sequence s 1 has three events, (p), (pqr), and (pr). Item p appears in the first event (p) and item r appears in the second event (pqr) of the first sequence, s 1 ; so, in this situation, there exists s-relation between them. On the other hand, second event (pqr) holds both item p and r; in this case, there exists i-relation between them.

• III.    Review of Works

In this segment, we have discussed an apriori based mining method, pattern growth mining, and FUSP - tree structure which will aid us to better understand our proposed approach.

• A.    Generalized Sequential Patterns (GSP)

GSP (Generalized Sequential Patterns) [2] is an apriori based sequential pattern mining algorithm which was proposed by Srikant and Agrawal in 1996. During mining, it generates lots of candidate sets and it tests them by multiple passes. The GSP algorithm to find the frequent sequential patterns is outlined as follows:

First Part: It scans the whole sequence database and finds length - 1 sequential patterns.

Second Part: To find the entire frequent sequential pattern, it scans the whole database iteratively. Each iteration discovers all the frequent sequential patterns with the same length.

In each iteration to find length-k sequential patterns (L k ), it does the following:

• 1.    By joining two length-(k-1) frequent sequential patterns if only their first and last items are different, it generates the length-k candidate sequential patterns, C k .

• 2.    It prunes the length-k candidate sequential patterns if any of its length-(k-1) contiguous subsequences is infrequent.

Then, it scans the whole database and finds the support for all the length-k candidate sequential patterns. If the support of any length-k candidate sequence is greater than or equal to min_sup, it puts this candidate sequence in length-k frequent sequential pattern (Lk).

It extends this procedure until there is any frequent sequential pattern or candidate sequence found.

However, GSP algorithm holds the difficulty that is described in formula 1 (see Problem 1).

Problem 1: For n sequential patterns (candidate + frequent), needs to scan the whole database n times to determine the support of each sequential pattern. When the size of the database increases, it generates the number of sequential patterns used in the mining algorithm supplementary and as a result the scans of whole database increases extremely as well. This problem is defined as follows:

D_s i _ze α Seq_num and Seq_num α D_scan                   (1)

Here, D_size denotes the total size of the database, Seq_num represents as the total number of sequential patterns and D scan means the total scans of the whole database. If D size increases, then both Seq num and D scan also increase and vice versa.

• B.    Pattern Growth Approach

At this time, we interpret the basic concept of pattern growth approach for sequential pattern mining since our proposed algorithm is based on it. Pattern growth approach is founded along the theory of conditional searching. Based on the definition 8, 9, and 10, this theory is illustrated as follows: prefix sequences are grown by finding smaller projection database from the larger database for each prefix sequence.

Then, recursively find frequent sequences from this projection database and add these frequent sequences to prefix sequence to find next frequent patterns. In sum, the frequent sequential patterns become larger and projection databases become smaller as the recursive calls go deeper and more mysterious. Granting to the theory of conditional searching, the pattern growth approach for sequential pattern mining is shown in Algorithm 1.

Algorithm 1: Pattern Growth Mine (pattern p, database D, int η)

Input: Sequence Database D, Minimum Support Threshold η, Frequent Pattern p. Initially, p set as null.

Output: Complete set of frequent sequential patterns Method:

• 1.    F → €

• 2.    for each item α in I do

  • 2.1.    if (Support of α ≥ η)

    • 2.1.1.    if item α is sequence related (see Definition 11) to p

      • 2.1.1.1.    then, q ← (p) U (α)

      • 2.1.1.2.    F → F U q

      • 2.1.1.3.    Construct α-Projection Database D α of D

      • 2.1.1.4.    F → F U Pattern Growth Mine (q, D α , η)

    • 2.1.2.    endif

    • 2.1.3.    if item α is itemset related (see Definition 11) to p

      • 2.1.3.1.    then, q ← (p U α)

      • 2.1.3.2.    F → F U q

      • 2.1.3.3.    Construct α-Projection Database D α of D

      • 2.1.3.4.    F → F U Pattern Growth Mine (q, D α , η)

    • 2.1.4.    endif

  • 2.2.    endif

• 3.    endfor

• 4.    return F

But, pattern growth approach holds the dilemma that is explained in formula 2 (see Problem 2). PrefixSpan [3] is a sequential pattern mining algorithm based on pattern growth approach and it also goes through the same difficulty.

Problem 2: In the nastiest case, for n frequent sequential patterns, needs to create n projection databases that mean one or more projection sequences for each projection database. The number of sequential patterns as well as projection databases generation rises in increasing order of the size of the whole database. This problem is illustrated as follows:

D_s i _ze α Seq_num and Seq_num α D p _ro j _ect                   (2)

Here, D_pro j _ect represents as the total number of projection databases. If D_size increases, then both Seq_num and D project increase as well and vice versa. (Look at problem 1 to be familiar with the meaning of D size and Seq_num)

Definition 12: If two nodes of a tree structure contain items from two different events of a sequence, then there exists sequence relation or s-relation and if two nodes hold items from the same event of a sequence, then there exist itemset relation or i-relation.

• C.    FUSP - Tree Algorithm

  To proficiently mine the sequential patterns, Lin et al.2008 proposed the FUSP-tree [6] structure and its maintenance algorithm. FUSP - tree consists of one root node labeled as ‘root’ and a set of prefix subtrees as the children of the root. Each node in the prefix subtrees contains item-name; which represents the node contains that item, count; the number of sequences represented by the portion of the path reaching the client, and node-link; links to the following node of that item in the next branch of the FUSP - tree. The FUSP - tree contains a HeaderTable which store frequent item, their count and the link of first occurrence node in the tree of that item. This table serves to find appropriate items or sequences in the tree. The construction process is similar to FP - tree [4] i.e. the construction process is executed tuple by tuple from first sequence to final. Only the conflict from the FP - tree is, the connection between two nodes is symbolized by‘s’ or ‘i’ as like IncSpan [7]. Here, symbol‘s’ indicates the sequence relation (see Definition 12) between two different events in a sequence and symbol ‘i’ indicates the itemset relation (see Definition 12) between two items in an event.

Mining process [5] of FUSP - tree [6] is similar to PrefixSpan [3] and FP-growth [4] algorithms. After the FUSP - tree is maintained, the final frequent sequences can then be found by a recursive method from the tree. This method determines the sequential patterns from the FUSP - tree structure by generating set of small projected trees from the large tree recursively. It generates no candidate sets, but it produces many projected trees for prefix sequences which suffer the same trouble defined in formula 2 (see Problem 2). Figure 1 shows a FUSP - tree structure with its Header Table for the sequence database shown in Table 1.

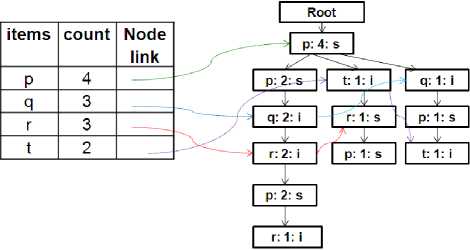
Fig. 1. FUSP - Tree with Header Table

• IV. Proposed Approach

We have described our mFUSP - tree structure and its mining approach to find frequent sequential patterns from sequence databases in this section. At first, our proposed approach constructs a modified fast updated sequential pattern tree (called a mFUSP - tree) structure to store only frequent items from the sequence database. Then, it generates the complete set of frequent subsequences from the mFUSP - tree structure without generating any intermediate projected tree. The algorithm for mFUSP -tree mining is given in Algorithm 2.

Algorithm 2: (mFUSP - Tree Mining: mining frequent subsequences from sequence database)

Input: Sequence Database and Minimum Support Threshold (min_sup).

Output: The complete set of frequent sequential patterns.

Method:

• 1.    Scan the sequence database to ascertain the length-1 frequent sequential patterns and their counts.

• 2.    Scan again sequence database to construct mFUSP -tree and its corresponding Header Table only for frequent items which are originated from step 1 by using Algorithm 3.

• 3.    Then, recursively mines the original mFUSP - tree to find out frequent sequential patterns without generating intermediate trees by using Algorithm 4.

• A. mFUSP - Tree Structure

In our study, a modified fast updated sequential pattern tree (called a mFUSP - tree) data structure along with Header Table is applied to store only frequent items from the sequence database. Each frequent item in the events of a sequence is inserted into the tree based on the events arranged in each sequence. Each branch of the tree is a sequence of the sequence database. It requires only two scans of database to construct the tree which reduces the scans of large original database significantly. One scan is for detecting the length-1 sequential patterns and their counts; another scan is required to build the mFUSP - tree structure along with Header Table based on length-1 patterns.

A modified fast updated sequential pattern tree (mFUSP - tree) is defined as follows:

• 1.    The root of the tree is a special virtual node with a label as Root and all sequences of the database add as child nodes to root.

• 2.    Each node in a mFUSP - tree registers four pieces of information: label, support count, identification and child link (label: count: identification: child link). Every node is labeled by a frequent item from the events of a sequence. The count of a node determines the number of sequences that share this node in their paths. Identification in a node is used to indicate if there exists a sequence relation (s-relation) or itemset relation (i-relation) between two nodes (see definition 12). If there exists s-relation, then set identification of the second node as “s” and if there exist i-relation, then place identification of the second node as “i”. Child link in a node is applied to connect the child nodes from this node.

• 3.    The mFUSP - tree structure maintains a Header Table, where each distinct frequent item with their support count is stored for sequential mining.

Construction process of mFUSP - tree is similar to FUSP - tree structure which executes tuple by tuple from first sequence to final. The algorithm for constructing a mFUSP - tree from sequence database is given in Algorithm 3.

Algorithm 3: (Construction of mFUSP - Tree from Sequence Database)

Input: Sequence Database and Minimum Support Threshold (min_sup).

Output: mFUSP - Tree, T.

Method:

• 1.    Scan (first scan) the sequence database and get length-1 sequential patterns with their support counts. Keep frequent length-1 patterns (those support count ≥ min_sup) to the Header Table.

• 2.    Create the root node of a tree T and label it as "Root". Initially current _node = root.

• 3.    for each sequence S i till the end of database (second scan)

  • 3.1    for each event e j in S_i

    • 3.1.1    for each item I in the e j

      • 3.1.1.1    if support of I ≥ min_sup, then

        • 3.1.1.1.1     if item I is sequence related ( see

• 3.1.1.1.1.1    if current_node has a child node c which c.label = I and c.identification = s, then set c.count += 1 and current_node

• 3.1.1.1.1.2    Otherwise,

  • 3.1.1.1.1.2.1    Create a New node label with I. 3.1.1.1.1.2.2 New node.count = 1.

  • 3.1.1.1.1.2.3    New node.identification = s.

  • 3.1.1.1.1.2.4     Store New node in the

• 3.1.1.1.1.2.5    Set current_node = New node 3.1.1.1.1.3 end if

• 3.1.1.1.2     end if

• 3.1.1.1.3     if item I is itemset related (see

• 3.1.1.1.3.1    if current_node has a child node c which c.label = I and c.identification = i, then set c.count += 1 and current_node = c.

• 3.1.1.1.3.2    Otherwise,

  • 3.1.1.1.3.2.1    Create a New node label with I 3.1.1.1.3.2.2 New node.count = 1.

  • 3.1.1.1.3.2.3    New node.identification = i.

  • 3.1.1.1.3.2.4     Store New node in the

• 3.1.1.1.3.2.5    Set current_node = New node 3.1.1.1.3.3 end if

• 3.1.1.1.4     end if

• 3.1.1.2     end if

• 3.1.2      end for

• 3.2        end for

= c.

current_node's successor link.

current_node's successor link.

• 4          current_node = root.

• 5       end for

• a.    Example of mFUSP - Tree Structure

In this fragment, we will try to describe the construction algorithm of mFUSP - tree by using an example. As input our algorithm just takes a sequence database and a minimum support threshold.

In our example, we have used the sequence database which is shown in Table 1 and let the minimum support is 50% or 2 (4*50% = 2).

The mFUSP - tree for the sequence database presented in Table 1 is constructed as follows: Scan the database to find the length-1 frequent sequential patterns with their support counts and keep them in the Table 2. Scan yet again the database and get the first sequence p(pqr)(pr). Insert this sequence into the initial tree with only one Root node. It creates a new node (p: 1: s) (i.e. labeled as p, with count set to 1 and identification to s) as the child of the Root node, and then derives the p-branch "(p: 1: s) → (p: 1: s) → (q: 1: i) → (r: 1: i) → (p: 1: s) → (r: 1: i)", in which arrows point from parent nodes to children nodes. Now, insert the second sequence (pt)r(pu). It starts from the Root again. Since the Root node has a child labeled with "p" and identification of this node is also s, then, p's count is just increased by 1, i.e., (p: 2: s) immediately. But, next item, t in first event of second sequence does not match with the existing child node of node (p: 2: s). So, create a new child node (t: 1: i) of node (p: 2: s) and then, derives the branch "(p: 2: s) → (t: 1: i) → (r: 1: s)

→ (p: 1: s)", but it ignores to insert item u as item u is infrequent according to the Table 2. Third sequence is most alike to the first sequence. So, just increment the count of nodes of the first branch and also, it does not insert the node (v: 1: i) as the child node of (p: 2: s) since item v is not frequent. This operation goes on until there is no sequence in the sequence database. Header Table stores p, q, r, and t with their support count because they are frequent. The complete mFUSP - tree along with its Header Table is shown in Figure 2.

Table 2. Length-1 Patterns and Their Support Counts

Length-1 Sequential Patterns	Support Count
p	4
q	3
r	3
t	2
u	1
v	1

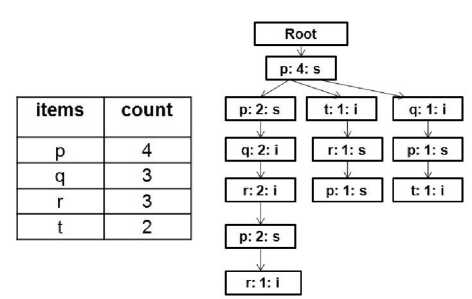
Fig. 2. mFUSP - Tree with Header Table

• b.    Characteristics of mFUSP - Tree

The key design points behind the mFUSP - tree are summarized as follows:

• 1.    mFUSP - tree is used to store each sequence of a sequence database in a compact data structure. Because, same sequences will share the same branch of the tree, only counts of the corresponding nodes increment. So, the size of the mFUSP - tree is much smaller than the size of the sequence database. The height of the tree is one plus the maximum length of the sequences in the database (one for root). The number of leave nodes of the tree, i.e., tree width is the number of distinct sequences in the database.

• 2.    Each node stores the corresponding counts of the items, so that, the mining algorithm can avoid the tedious support counting during mining. That means, it can lessen the repeated scanning of large database during mining.

• 3.    Identification store in each node is used to easily specify the sequence relation or itemset relation between nodes.

• 4.    Compared with the FUSP - tree [6], links stored in the FUSP - tree [6] to find the next node of same item from the next branch help us to locate the

frequent items easily without scanning each projected trees during mining. Our proposed tree structure avoid this extra burden by not storing link information in the tree, as our proposed mining algorithm is efficient enough to discover frequent sequential patterns without these link information. Our tree structure only links the children nodes from the parent.

Definition 13: For any node labeled as e i , all the nodes in the path from the root (excluded root) of the tree to this node form a prefix sequence of e_i.

For instance, in the Figure 2, for node (q: 2: i) in the first branch, the prefix sequence is (p)(pq).

Definition 14: for any node labeled as e i , all the nodes in the path from e i (itself excluded) to leave node form a suffix sequence of e i . There are several children of e i in the tree, and each branch from a child to a leaf node will represent as a suffix sequence and all these suffix sequences are called the suffix tree of e_i.

For example, in the Figure 2, for node (q: 2: i) in the first branch, the suffix sequence is (r)(pr). Again, in the Figure 2, node (p: 4: s) has three suffix sequences

(pqr)(pr), (t)(r)(p), and (q)(pt). All these suffix sequences are called the suffix tree of node (p: 4: s) and node (p: 4: s) is the root of this suffix tree.

Lemma 1: Given a sequence database S, the support count of each sequential pattern can be obtained from the count of each node corresponding to this sequential pattern.

Justification: Based on the mFUSP - tree construction process, each sequence in S is mapped to one path in the mFUSP - tree. And all frequent items in each sequence are completely stored in the mFUSP - tree. Given a sequential pattern α = (α 1 , α 2 , . . . , α n ). Following the child link of each item, we can traverse the suffix trees of these nodes. Assume that P denotes a complete set of paths that sequence α occurs in the suffix trees. Let n denote the last node in a path p (p € P), the support count of α in p is equal to the count of n node. Therefore, for each p in P, we can accumulate the count of each last node of each p to get the complete support count of sequence α.

Based on this lemma, we can conclude that our algorithm can avoid multiple scanning of large database during mining since we can get the support count of each sequential pattern from the mFUSP - tree. Because monotonous multiple scanning is required to get the support count of each pattern from the large database. Our algorithm requires only twice scans of database owing to construct the mFUSP - tree.

• B. Mining Algorithm of mFUSP - Tree

mFUSP - tree mining algorithm is designed for efficiently mining sequential patterns from the mFUSP -tree structure. During mining, this algorithm utilizes the original mFUSP - tree for the entire mining and does not rebuild intermediate trees for projection databases like PrefixSpan [3] and FUSP - tree [5]. Moreover, it does not scan the original database multiple times during mining that GSP [2] does.

Lemma 2: Given a mFUSP - tree T of a sequence database S, each frequent sequential pattern can be derived from the original mFUSP - tree structure, T without generating any intermediate projected tree.

Rationale: We can find any node from the suffix tree of a node labeled as e i by using the links of the children node of e i . If we store only the prefix node labeled as e i , then, using the links of the child nodes, we can discover the frequent events from the suffix tree of e i . For this reason, we employ suffix rootsets that store only the prefix node labeled as e_i. Rootsets are used to virtually represent the suffix trees without the need to physically store each suffix tree. The main idea is, find frequent events from the suffix trees of the last frequent event in a m-prefix sequence and add these frequent events to m -prefix sequence to enlarge this subsequence to m+1 -prefix sequence recursively. In closing, our algorithm can avoid generating any projected tree during mining by storing just the prefix nodes (roots) of the suffix trees physically instead of storing whole suffix trees.

The algorithm for mining sequential patterns from the mFUSP - tree is described in Algorithm 4. This algorithm begins from the Header Table. For each frequent item α in the Header Table, it always tries to get the first-occurrence node with labeled α from each branch of the original tree and stores these nodes in the rootset. The first-occurrence nodes of a symbol are found using depth-first-search of the tree. The algorithm of detecting the first-occurrence node is given in Algorithm 5.

This algorithm applies two rootsets, one to store the s-relation nodes and another to store the i-relation nodes related to an item, α. If the sum of the counts of all nodes in the rootset for s-relation nodes related to α is greater than or equal to the minimum support threshold, then α is appended to the sequential pattern list. Next, using this rootset, find the next frequent prefix subsequence (α)(α₁) or (αα 1 ) or both from the α-suffix tree. The same attitude is employed for the rootset that stores i-relation nodes. This process goes along for each prefix subsequence until there is no suffix tree for that prefix subsequence for search. This method is carried out for each frequent item in the Header Table to retrieve all frequent sequential patterns.

Algorithm 4: (mFUSP - tree Mine (Rootset, p): Mining Sequential Patterns from mFUSP - tree)

Input: mFUSP - tree with Header Table and Minimum Support Threshold (min_sup).

Output: The Complete Set of Frequent Sequential Patterns.

Global Variable: Rootset_s to store s-relation nodes, Rootset_i to store i-relation nodes, Track to store each root node.

Other Variable: F to store frequent sequential patterns list and p to store each pattern.

Initial: Initially, Rootset_s stores Root of the original tree and set both F and p as null. At first, call the mFUSP - tree Mine () of Algorithm 4 by passing Rootset_s and p.

Method:

• 1.    F → €

• 2.    for each frequent item α in the Header Table

  • 2.1    Rootset_s = new Rootset()

  • 2.2    Rootset_i = new Rootset()

  • 2.3    for each root node R of the Rootset

    • 2.3.1    Track = R

    • 2.3.2    for each child node N of R

      • 2.3.2.1    First-Occurrence-Node(α,N,0,0) [Describe in Algorithm 5]

    • 2.3.3    end for

  • 2.4    end for

  • 2.5    if (the sum of the counts of root nodes in the Rootset_s ≥ min_sup), then

    • 2.5.1    q ← (p) U (α)

    • 2.5.2    F → F U q

    • 2.5.3    F → F U Call mFUSP-tree Mine (Rootset_s, q)

  • 2.6    end if

  • 2.7    if (the sum of the counts of root nodes in the Rootset_i ≥ min_sup) ,then

    • 2.7.1   q ← (p U α)

    • 2.7.2  F → F U q

    • 2.7.3    F → F U Call mFUSP-tree Mine (Rootset_i, q)

  • 2.8    end if

• 3.    end for

• 4.    return F

Algorithm 5: (First-Occurrence-Node (α, N, Mark_s, Mark_i): To Find First Occurrence Node that Labeled as α in the mFUSP- tree).

Input: Frequent Item, α and child node N of Root node R from Rootset, Mark_s variable is used to find only one s-relation node labeled as α from a branch and Mark_i variable is used to find only one i-relation node labeled as α from a branch.

Output: The First Occurrence nodes those Labeled as α.

Global Variable: Mark variable is used to keep track if the parent node's label of a node equal to the root node's label. Initially, Mark set as 0.

Method:

• 1.    if (N. label = Track. label)

  • 1.1    set Mark as 1

• 2.   end if

• 3.   if ( N. label = α), then

  • 3.1    if (Track. label = root)

    • 3.1.1   Append N to Rootset_s

    • 3.1.2   Mark_s set as 1

  • 3.2    else if (N. identification =  “i” && Mark = 0

• 3.2.1   Append N to Rootset_i

• 3.2.2   Mark_i set as 1

• 3.3    else if (N. identification = “i” && Mark = 1 && Mark_i = 0)

  • 3.3.1   Append N to Rootset_i

  • 3.3.2   Append N to Rootset_s

  • 3.3.3   Mark_i set as 1

  • 3.3.4   Mark_s set as 1

• 3.4    else if (N. identification = “s” && Mark_s = 0)

  • 3.4.1    Append N to Rootset_s

  • 3.4.2    Mark_s set as 1

• 3.5    end if

• 4.    end if

• 5.    for each child node, n of node N

  • 5.1    First-Occurrence-Node (α, n, Mark_s, Mark_i)

• 6.    end for

• a. Example of Mining Algorithm of mFUSP - Tree

For proper understanding of our proposed mining approach, in this section, we will try to illustrate our algorithm step by step with the aid of an example. As for input, our mining algorithm just takes mFUSP-tree with Header Table and minimum support threshold (min_sup).

The algorithm’s steps are keyed out below using the mFUSP - tree structure established in Figure 2:

Step 1: The first item in the Header Table is 'p'. From the Root node of the mFUSP - tree shown in Figure 2 determines the first-occurrence nodes labeled as 'p' using depth-first-search. The first-occurrence node of item 'p' is (p: 4: s) node. The count of this node is 4 ≥ minimum support threshold and Identification of node (p: 4: s) is “s”. So, the frequent sequential pattern is (p) and now the list of mined frequent sequential patterns is {(p): 4}. The mining of frequent 2-sequences that start with item 'p' would continue with the suffix tree rooted at node (p: 4: s) pictured in Figure 3 [colored portion]. Again, for item 'p' in the Header Table, initiates exploring to obtain first-occurrence nodes labeled as 'p' from the root node (p: 4: s). The first-occurrence nodes labeled as 'p' from root node (p: 4: s) are (p: 2: s), (p: 1: s) and (p: 1: s). The sum of counts of these nodes is 4 ≥ minimum support threshold. Identification of these nodes is “s”, so that, the frequent sequential pattern is (p)(p) and at this moment the list of mined frequent sequential patterns is {(p): 4, (p)(p): 4}. Yet again, for item 'p' in the Header Table, finds a first-occurrence node (p: 2: s) labeled as 'p' from the suffix trees rooted at nodes (p: 2: s), (p: 1: s) and (p: 1: s) depicted in Figure 4 [colored portion]. The count of node (p: 2: s) is 2 ≥ minimum support threshold. As identification of this node is “s”, appends it to (p)(p) sequence as a s-relation item to create frequent 3-sequence (p)(p)(p) and at this time the list of mined frequent sequential patterns is {(p): 4, (p)(p): 4, (p)(p)(p): 2}. At that point is, no suffix tree rooted at node (p: 2: s) for search described in Figure 5 [colored portion]. So, no frequent 4-sequences exist for (p)(p)(p) sequence and stop here.

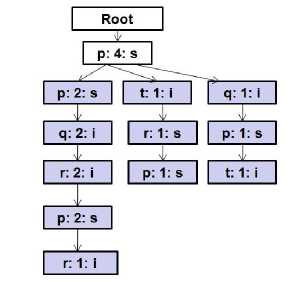
Fig. 3. Suffix tree rooted at node (p: 4: s) for prefix sequence "(p)"

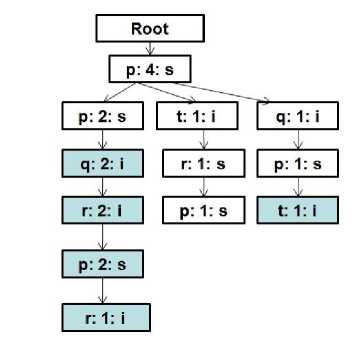
Fig. 4. Suffix trees rooted at (p: 2: s) and (p: 1: s) for prefix sequence "(p)(p)"

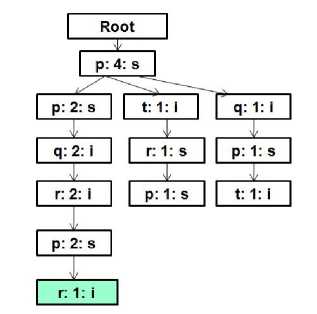
Fig. 5. Suffix tree rooted at node (p: 2: s) for prefix sequence "(p)(p)(p)"

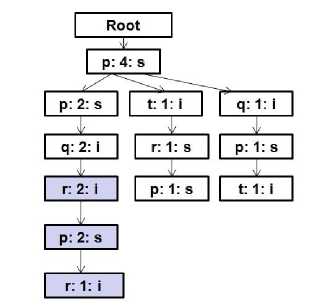
Fig. 6. Suffix tree rooted at node (q: 2: i) for prefix sequence "(p)(pq)”

Backtrack and go again for item 'q' on the Header Table and discovers a first-occurrence node (q: 2: i) labeled as 'q' from the suffix tree of node (p: 2: s) and there is no node labeled as “q” in the suffix tree rooted at node (p: 1: s) illustrated in Figure 4 [colored portion]. The count of this node is 2 ≥ minimum support threshold. Identification of node (q: 2: i) is “i”. So, node (q: 2: i) is considered as a i-relation node. So, the frequent sequential pattern is (p)(pq) and currently, the list of mined frequent sequential patterns is {(p): 4, (p)(p): 4, (p)(p)(p): 2, (p)(pq): 2}.

Persist in this operation for the frequent 4-sequences that begin with the (p)(pq) sequence from suffix tree rooted at node (q: 2: i) demonstrated in Figure 6 [colored portion] and come up only one frequent pattern (p)(pq)(p): 2. No suffix tree left to search rooted at node (p: 2: s) provided in Figure 5 [colored portion].

Applying this same methodology, we can find the complete set of frequent sequential patterns starting with item 'p' and the frequent sequential patterns are {(p): 4, (p)(p): 4, (p)(p)(p): 2, (p)(pq):, (pt): 22, (p)(pq)(p): 2, (p)(pqr): 2, (p)(pqr)(p): 2, (p)(pr): 2, (p)(pr)(p): 2, (p)(q): 2, (p)(q)(p): 2, (p)(qr): 2, (p)(qr)(p): 2, (pq): 3, (pq)(p): 3, (pqr): 2, (pqr)(p): 2, (p)(r): 3, (p)(r)(p): 3, (pr): 2, (pr)(p): 2}.

Step 2: This same procedure will be repeated for the frequent items q, r, and t; those are stored in the Header Table. Finally, the complete set of frequent sequential patterns are {(p): 4, (p)(p): 4, (p)(p)(p): 2, (p)(pq): 2, (p)(pq)(p):  2,  (p)(pqr):  2,  (p)(pqr)(p):  2,  (p)(pr):  2,

(p)(pr)(p): 2, (p)(q): 2, (p)(q)(p): 2, (p)(qr): 2, (p)(qr)(p): 2, (pq): 3, (pq)(p): 3, (pqr): 2, (pqr)(p): 2, (p)(r): 3, (p)(r)(p): 3, (pr): 2, (pr)(p): 2, (pt): 2, (q): 3, (q)(p): 3, (qr): 2, (qr)(p): 2, (r): 3, (r)(p): 3, (t): 2}.

• C. Completeness and Correctness – Theoretical Proof

The primary purpose of all kinds of mining algorithms is to determine the perfect set of frequent patterns for the specified minimum support threshold. When an algorithm can get those patterns without losing anyone, then we can suppose that the algorithm is complete. On the other hand, the correctness of an algorithm is to determine the correct patterns with accurate frequency which are interesting for the given minimum support threshold. When an algorithm has both of these standards, then the algorithm is complete and correct. Like other existing sequential pattern mining algorithms, our proposed mining algorithm is also complete and correct that we have theoretical demonstrated in this fragment.

Let T denote the complete mFUSP - tree and L k the complete set of k-sequential patterns. Before giving the proof, we briefly summarized the major steps of the mFUSP - tree mining algorithm. These steps will help us to ignore the details of algorithm that not related to the proof.

• 1.    Find all L₁ patterns in the construction of the mFUSP - tree.

• 2.    For each patterns α in L_k-1 (k ≥ 2).

  • 2.1    Traverse α’s suffix mFUSP - tree in T, denoted as T|α, and calculate the count of each item in L 1 from T|α by using Lemma 1.

  • 2.2    Obtain a k-sequential pattern, denoted as α', by appending either an item in the last itemset of α or a new itemset after the last itemset of α if the support count of α' satisfies minimum support threshold.

  • 2.3    Put all those patterns α' into L_k if their support counts satisfy minimum support threshold.

• 3.    Recursively find L k+1 sequential patterns with prefix α' in T|α'.

• Theorem 1:    Every sequential pattern must be

obtained by the mFUSP - tree mining algorithm.

Proof: For each item i in L 1 , we traverse i’s suffix mFUSP - tree, denoted as T|i, from T. This theorem can be proved by induction.

Basis: If k = 1, meaning that there is only one item in each pattern, then all patterns in L1 can be found by the step 1 of the mFUSP - tree mining algorithm.

Inductive step: We consider algorithm can find all L k sequential patterns. Suppose we are given an L k sequential pattern denoted as x = {i 1 , i 2 ,…, i k }. This means step 2.1 of the algorithm will traverse < i 1 , i 2 ,…, i k- ₁ >’s suffix mFUSP - tree T|< i₁, i₂,…, i_k-1 >. Based on the Lemma 1, the support count of each sequential pattern can be derived from the mFUSP - tree. Hence, all the pattern information related to i k-1 will be kept in T|< i 1 , i 2 ,…, i k-1 >. Thus, step 2.2 of the algorithm can find x' = {i 1 , i 2 ,…, i k-1 } from T|< i 1 , i 2 ,…, i k-1 >. Finally, i k can be appended after x' to form pattern x. Then, we can find all sequential patterns of L k by checking if a pattern in L k satisfies minimum support threshold. We did this in step 2.3. Therefore, the mFUSP - tree mining algorithm can find all sequential patterns.

• Theorem 2:    The sequential patterns obtained by the mFUSP - tree mining algorithm are correct.

• 2.2, and 2.3, every sequential pattern in L 1 and L k (k ≥ 2) must be frequent (i.e. satisfy minimum support threshold).

Proof: Because of the examination done in steps 1,

Based on these theorems above, we have concluded that the mFUSP - tree mining algorithm is complete and correct.

• V.    Performance Analysis

We have evaluated the performance of our proposed mFUSP - tree mining approach with other three existing approaches GSP [2], PrefixSpan [3] and FUSP-Tree Based mining [5] for two real datasets and a synthetic dataset. All the experiments were conducted on a 2.80GHz Intel(R) Pentium(R) D processor with 1.5GB main memory, running on Microsoft Windows 7. All the programs were written in NetBeans IDE 6.8 with JDK 6.

• A.    Datasets

We have used three datasets, two real-datasets, BMS-WebView-1 [8], and BMS-POS [8], as well as a Synthetic dataset T10I4D100K [8] for evaluation of experimental results. We use these datasets by considering each transaction as a sequence and each item of the transaction as a single item element in that sequence. Obviously, while considering these datasets for sequential pattern mining, they will also generate long sequential patterns. The properties of these datasets, in terms of the number of distinct items, the number of sequences, the maximum sequence size, the average sequence size, and type are shown below by a Table 3.

• B.    Experimental Result

Execution times after running four algorithms for different minimum support thresholds by using three datasets (T10I4D100K, BMS-WebView-1, and BMS-POS) are presented at this juncture.

Table 3. Properties of Experimental Datasets

Dataset	Distinct Items	No. of Sequences	Max Size	Avg. Size	Type
T10I4D100K	870	100000	29	10.1	Synthetic
BMS-WebView-1	497	59602	267	2.5	Real
BMS-POS	1657	515597	164	6.5	real

• a.    The Comparison Between GSP and mFUSP - Tree

Three datasets, including a synthetic dataset (i.e. T10I4D100K) and two real datasets (i.e. BMS-WebView-1 and BMS-POS), were used to examine the execution time of both GSP and mFUSP - tree with respect to minimum support threshold. Figure 7 shows the execution time results for T10I4D100K, BMS-WebView-1 and BMS-POS, respectively. The results indicate that the mFUSP - tree mining algorithm is much faster than GSP. The results are as expected; because GSP needs scanning these datasets multiple times to find the support count of each sequential pattern. When the number of sequences in each dataset increases, the amount of scans increases as well and as a consequence, the execution times of GSP algorithm raise. On the contrary, mFUSP -tree mining method can determine the support count of each pattern from the node’s count of the mFUSP - tree structure effortlessly and moreover, it calls for only twice scans of these datasets to build the mFUSP - tree from these datasets.

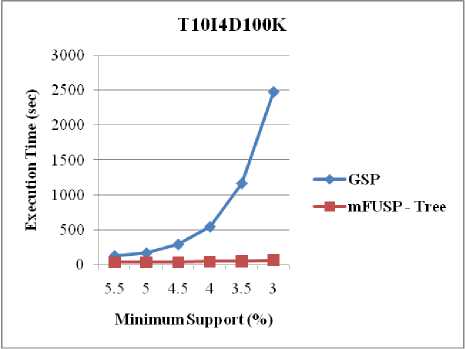
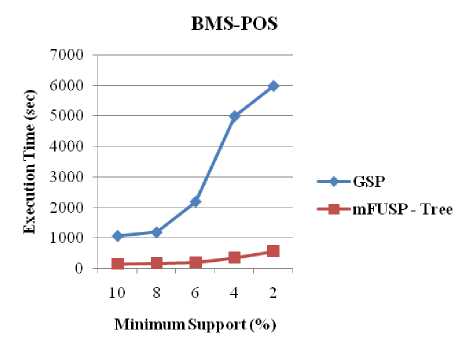
Fig. 7. Execution Time vs. Minimum Support between GSP and mFUSP - Tree

• b.    The Comparison Between PrefixSpan and mFUSP -Tree

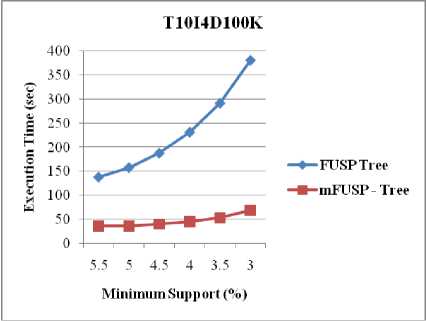
Figure 8 demonstrates the execution time results for T10I4D100K, BMS-WebView-1 and BMS-POS, respectively due to compare the execution time of both PrefixSpan and mFUSP - tree with respect to minimum support threshold. The result is quite encouraging; because PrefixSpan produces projected intermediate tree from these datasets for each sequential pattern. We know that number of sequential pattern generation increases when the size of the database increases and hence, the number of intermediate tree generation increases as well. This similar dilemma influences PrefixSpan algorithm. For this reason, PrefixSpan requires more times than mFUSP - tree mining to uncover frequent sequential patterns from these large datasets (T10I4D100K, BMS-WebView-1, and BMS-POS) as our proposed method does not generate intermediate trees during mining.

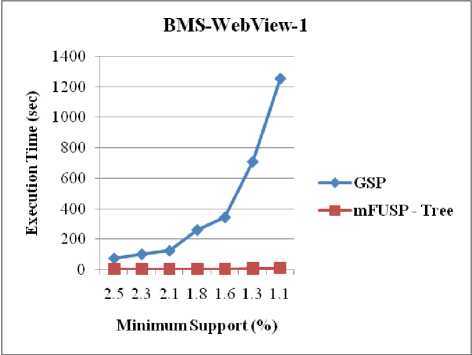
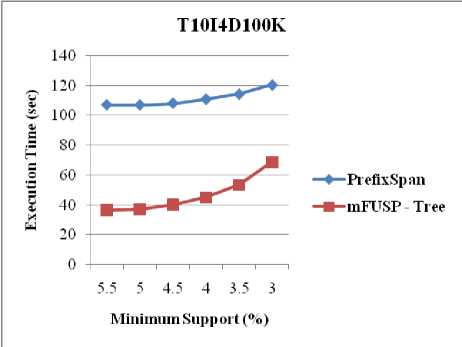
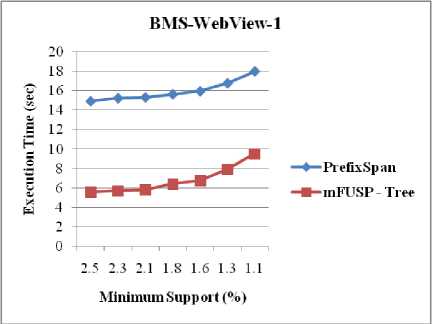
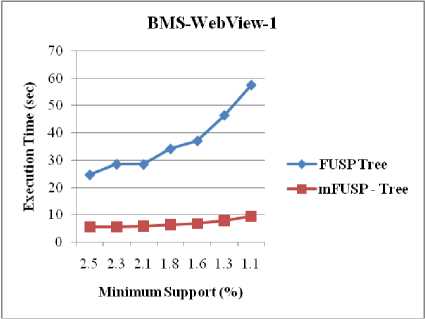
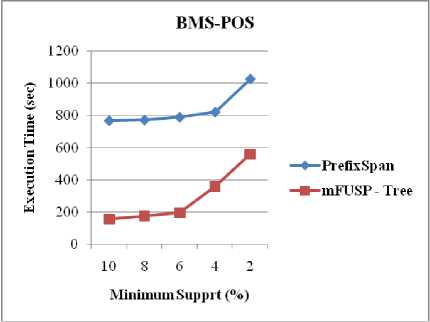
Fig. 8. Execution Time vs. Minimum Support between PrefixSpan and mFUSP - Tree

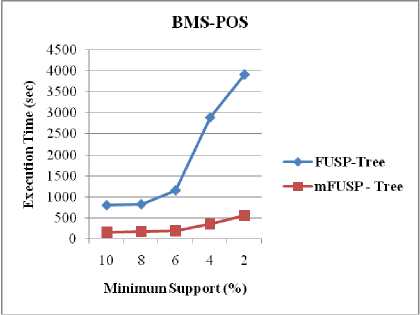
Fig. 9. Execution Time vs. Minimum Support between FUSP - Tree and mFUSP - Tree

• c.    The Comparison Between FUSP - Tree and mFUSP -tree

Figure 9 is employed for evaluating the performance of both FUSP - tree and mFUSP - tree mining with respect to minimum support threshold by using three datasets, T10I4D100K, BMS-WebView-1 and BMS-POS, respectively. FUSP - tree almost similar to the mFUSP -tree except that it generates intermediate trees for each sequential pattern from these datasets and it stores additional linking information in its node. The results shown in Figure 9 point out that as an effect of intermediate trees generation and link updating procedure of each projected tree, FUSP - tree entails supplementary times during mining than mFUSP - tree mining for these large datasets.

• C.    Completeness and Correctness

In this section, we have substantial demonstrated that the proposed algorithm is complete and correct.

The completeness of the proposed algorithm can be verified by comparing the total numbers of patterns generated for various minimum support thresholds. From Figure 10, we can perceive that the proposed algorithm produces the same number of patterns as GSP [2], PrefixSpan [3] and FUSP - tree [5] mining generate for datasets T10I4D100K, BMS-WebView-1 and BMS-POS respectively. From this figure, we can also observe that the total number of frequent patterns generation inversely proportional to the minimum support threshold. That implies, if the values of the minimum support thresholds decrease, then the total number of frequent patterns generation increases and vice versa. Since for all datasets, the proposed algorithm has generated complete set of frequent sequential patterns as existing algorithms generate, so it proves the completeness of the algorithm presented in this paper.

Table 4 has presented the sequential patterns obtained from the four algorithms for the sequences which are shown in Table 1. We can realize from this table that, these four algorithms generate the same frequent sequential patterns with the same frequencies for the same minimum support threshold. In other word, we can state that, the proposed algorithm gives the same result as GSP [2], PrefixSpan [3] and FUSP - tree [5] mining methods produce that demonstrates the correctness of the algorithm given in this paper.

Thus, based on the exceeding discussion, it can be said that the proposed mFUSP - tree mining algorithm is complete and correct.

Table 4. Sequential Patterns Obtained from Four Algorithms for

Database Shown in Table 1

Algorithms	Total Patterns	Sequential Patterns (Pattern : count)
GSP	29	(p): 4. (q): 3, (r): 3, (t): 2, (pXp): 4, (pXq): 2, (pq):3, (pXO: 3, фг): 2, (pt): 2, (qXp): 3, (qr): 2, (rXp): 3, (pXpXp): 2, (jpKpq): 2, фХрг): 2, (pXqXpX 2, (pXqr): 2, (pqXp): 3, (pqr): 2, (pXrXp): 3, (piXp): 2, ( 2, (pXpqXp): 2, ФХиО 2. фХргХр): 2, (pXqrXp): 2, (pqrj(p): 2, (pXpqtXp)- 2,
PrefciSpan	29	(p): 4, (pXp): 4. (pXpXp): 2, (pXpq): 2. (pXpqXp): 2, (pXpqr): 2, (p)(pqr)(p): 2, (pXpr): 2, ФХргХр): 2, ФХчХ 2, (рХчХрХ 2, (pXqr): 2, (pXqrXp): 2, (pq) 3, (pqXp): 3, (pqr): 2, (pqrXp): 2. (pXr): 3, фХгХФ): 3, фг): 2, (рг)ф): 2, (pt): 2, (q): 3, (qXp): 3, (qi): 2, (qr)(p): 2, (r): 3XrXp):3,(t):2
FUSP - tree	29	(P): 4: (pXp): 4, (pXpXp): 2, (pXpq): 2: CpXpqXp): 2, (pXpqr): 2, (pXpqrXp): 2, (pXpr): 2, (pXpiXp); 2, ФХч): 2, (рХчХрХ 2, ФХчг): 2, (pXqr№): 2, (pq): 3, (pqXp): 3, (pqr): 2, (pqrXp): 2, №): 3, ФХ=:ХФ): 3, фг): 2, (рг)ф): 2, ФО: 2, (q): 3, (qXp): 3, (qr): 2, (qrXp): 2, (r): 3,(г)ф):3,®:2
mFUSP- tree	29	(P): 4, фХр): 4, (pXpXp): 2, ф}фч): 2, (рХрчХр): 2, (pXpqr): 2, (pXpqiXp): 2, ф)фг): 2, ф)фг)ф): 2, (pXq): 2, (pXq№): 2, фХчО: 2, (РХЧОФХ 2, (pq): 3. фЧ)ф): 3. (pqr): 2, (pqrXp): 2, (pXO: 3, ФХ0Ф): 3, (pr): 2, фг)ф): 2, (pt): 2, (q): 3. (qXp): 3. (qr): 2, (qrXp): 2, (r): 3, (г)ф): 3, (t): 2.

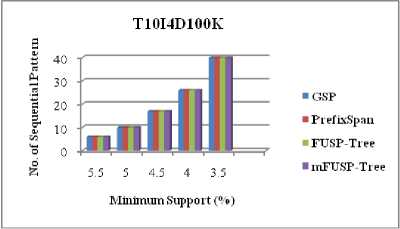
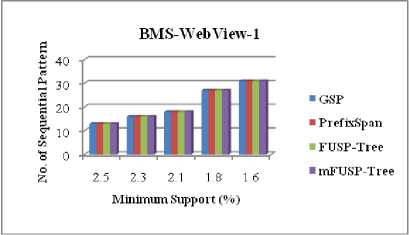
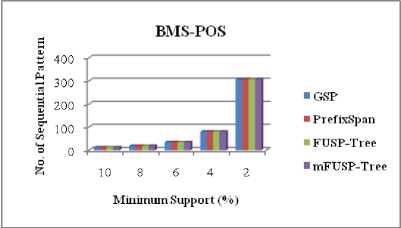
Fig. 10. Comparison between No. of Sequential Patterns and Minimum Support

• VI.    Conclusion

To achieve efficient mining sequential patterns, a compact data structure, called a mFUSP - tree, is proposed to store and compress entire sequence database and a mining algorithm, named mFUSP - tree mining, is developed to ascertain the complete set of frequent patterns from the mFUSP - tree. Because of this tree structure, we can resolve many problems that have other existing algorithms like GSP, PrefixSpan and FUSP - tree mining. First of all, we can compact larger sequence database into smaller tree structure because of partaking the same branch of the tree for the similar sequence of database and as well, for storing frequent items. Subsequently, our mining algorithm can avoid the multiple scanning of large database attributable to storage of counts in the tree’s node; only require twice scans of database to build the mFUSP - tree. Next, the link information is not stored in the mFUSP - tree structure then that our proposed mining algorithm can pay no attention to the link updating process. Ultimately, the mFUSP - tree structure is too efficient for incremental mining that we will describe in our future study. In order that, the performance of our proposed mining method enhances in favor of these gains of the mFUSP - tree structure. Likewise, we want to point out that mFUSP -tree mining algorithm does not scan the large database numerous times as well as does not generate intermediate projected trees as a result of depth first search from parent node to child nodes that shrinks the time complexity of the algorithm and our experimental results provide evidence for performance enhancement of the method that has demonstrated in this paper.