Многоальтернативное отождествление объектов с оценкой максимального правдоподобия однотипных параметров

Развитие технологий снижения заметности объектов [1–3] определяет важность совершенствования способов и средств мониторинга (СМ) на основе комплексного анализа разнородных демаскирующих признаков в различных физических полях и диапазонах частот [1; 2]. Так, принципы построения системы измерительносигнатурной разведки MASINT – Measurement And Signature Intelligence базируются на совместном применении активных и пассивных средств радиолокационного обзора, оптикоэлектронных, акустических, сейсмических и магнитометрических датчиков. В системах территориального контроля, раннего обнаружения и распознавания подвижных наземных целей REMBASS – Remotely Monitored Battlefield Sensor System и SOTAS – Stand off Target Acquisition используются оптико-электронные, акустические и сейсмические разведывательносигнализационные приборы с единым центром сбора и обработки информации [1].

За счет анализа широкой номенклатуры данных (сведений), поступающих от независимых источников, парируются пропуски целей в отдельных каналах поиска (наблюдения), что способствует повышению оперативности, полноты и достоверности оценки обстановки [1; 2].

В процессе совместного функционирования СМ требуется выполнять отождествление добываемых данных (сведений), суть которого за-

ключается в установлении идентичности целей в различных каналах путем сопоставления их однотипных параметров и принятии решения о принадлежности независимых признаков идентификации одному и тому же объекту [4; 5].

В предлагаемой работе на основе критерия минимума среднего риска [4; 5], обеспечивающего высокую надежность принимаемых решений при малом числе признаков идентификации [4], выполнен синтез алгоритма и найдены статистические характеристики эффективности многоальтернативного отождествления объектов [4] при наличии пропусков в сопоставляемых массивах и использовании оценок максимального правдоподобия [6] неизвестных однотипных параметров.

Цель работы – исследование возможностей отождествления объектов в условиях априорной неопределенности признаков идентификации.

1. Синтез алгоритма отождествления объектов с оценкой максимального правдоподобия однотипных параметров

Будем полагать, что отождествление выполняется между I объектами, выявленными пер-

вым СМ, с массивом признаков идентификации

£ ( n ) ^ i

в n -мерном пространстве, i = 1... I , n >  1,

и J объектами с набором однотипных параме-

тров

£ ( n ) ^ j

,

j = 1... J ,

вторым СМ. Значения

n >  1, зафиксированных

£ ( n )"l Г £( n )

^^v I и I ^ j I определе-

ны со среднеквадратическими ошибками (СКО)

~ ⁽ "  )   _ ⁽ "  )

a i и a j , i = 1... I , j = 1... J , n >  1 соответственно.

В общем случае I ^ J; массив I I(j) I, j = 1. J, n > 1 может содержать компоненты, не ото-( ") ждествляемые ни с одним из элементов Iх i , i = 1. I, n > 1 и наоборот, что характерно для случаев пропуска результатов поиска (наблюдения) в одном из каналов; максимальное количе- ство целей, пропущенных вторым СМ, равно I .

Для отождествления объектов с признаками идентификации rI⁽ " ) ] и rI⁽ " ) | , i = 1 . 1 , j = 1 . J , n >  1 по критерию минимума среднего риска R_ps требуется установить принадлежность I компонентов | I⁽ " ) ] , i = 1 . 1 , n >  1, определенных первым СМ, K i = I + J объектам из числа

J зафиксированных или I пропущенных вто- рым СМ с массивом значений

5 ⁽ " )

^I к

к = 1 . K I ,

n >  1, при условии [4; 5]

( i , к ) = arg min Rp. ,(1)

i=1. I, к=1. KI где

IK

Rps = E E RikPps (i("); Iк")),(2)

i=1 к=1            77

E P ap ( I^) ) = 1, i = 1

E.P11'к")I(n*1- 1,(4)

к=1   17

I K I

EE P p. ( 1¹ " ) ; I к" ⁾ ) = 1. i = 1 к = 1

Полагая по аналогии с [6], что риски принятия правильных решений равны нулю, а все неправильные решения приводят к одинаковым информационным потерям, т. е.

^R ik = R 0 ( ¹ -5 ii ' )( ¹ -5 кк ' ) , ⁽⁵⁾

где R ₀ – положительно определенная величина; 5_a p — символ Кронекера, путем подстановки (5) в (2), а полученного результата в (1), находим правило многоальтернативного отождествления объектов

( i , к ) = arg max P p. ( I \ I к ^ .           (6)

i=1. I, к=1. KI

С учетом (3) правило (6) представим в виде

( i , ^к ) = arg max P ap ( ^I ^ ^ ■ P [ ^I ^ i = 1. I ,      ^{V             1}

к = 1 . K I

I ⁽ " ) | .(7)

Условная вероятность ситуации отождест-

R_ik – риск принятия решения об отождествле-

нии объектов с однотипными параметрами

и

5 ⁽ " )

^I к

E ⁽ " )

^I i

, i = 1 . 1 , к = 1 . K I , n >  1,

вления объектов с однотипными параметрами Г I⁽ ". ^] и Г I⁽ /" ) ] , i = 1 . 1 , к = 1 . K I , n >  1, находится как произведение вероятностей того, что

P ps ( I⁽ n ) ; I⁽ n ) ) = P ap ( |⁽ n ) ) • P | I⁽ n ) I⁽ n ) |      (3)

– апостериорная вероятность гипотезы об ото-

ждествлении объектов с однотипными параметрами [ I⁽ " H и [ I ( " ^)- | , i = 1 . 1 , к = 1 . K i , n >  1,

определенная в соответствии с теоремой гипо- ( n )

тез [4], Pap I Xi   — априорная вероятность ус ловия отождествления i-го объекта, i = 1.1,

при гипотезе отождествления пары объектов ( i , к ) значения I⁽ " ) , i = 1 . 1 , n >  1 принадлежат некоторой области Q ( _n ) , n >  1 с размерами, определяемыми порогом принятия решения [4] в окрестности I ⁽ " ) , к = 1 . K i , n >  1, а любые другие значения I⁽ " ) , p ^ i , p = 1 . 1 , n >  1 располагаются за ее пределами [4; 7]:

p I 5 ⁽ " ) E ⁽ " ^P I ^I к ^I i

–

условная вероятность ситуации

отождествления к -го, к = 1 . K i , и i -го, объектов, выявленных различными СМ.

Ввиду того, что гипотезы, решения ации отождествления целей образуют

i = 1 . 1 ,

и ситу-полную

группу несовместных событий, для P_аp

Г5(n) E(nn PI I к I i I требования [5]:

и P p. ( I⁽ " ) ; I⁽ к" ) )

( I⁽ " ’ ) •

выполняются

P |I (к" ^n )} =P |I (к" )|I( n); ^( n )}x хП I1 -P (I("^"); Q(n)))               (8)

p=1, p ^ i к = 1. KI, где p Г 5(") E ("). q ) _

^P I ^I к ^I i ^; ^ ( n ) I

n

= f w 11 к ’| I¹ n ‘ ) n d 5 * r ¹ ,                 <9>

Ц " )                   r = 1

k = 1 . K I , i = 1 . I , n >  1,

w

I

^{( n} ) k

E ^{( n} )

¹ i

; 1n)

A* ;

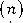
i

n

w

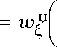
г ⁽ n )

¹ k

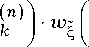
e ⁽ n )

¹ i

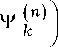
2 n j ( i⁽ r ) ) 2 + ( i* ^r ) ) r = 1 ^L

= X 2 "

– закон распределения однотипных параметров при априорной неопределенности их истинных значений Т kn ) , k = 1 . K j , n >  1,

x exp

jb (;«_;W)2

r = 1

w

A

I

^{( n} ) k

Т

^{( n} ) k

2 jL [ ( i ⁽ r ) ) 2 + ( i⁽ r ) ) 2

r = 1 ^L

^^^^=^^^^=- X

2 « Z ( i k * ) ²

r = 1

Из (9) и (14) следует, что при существенном

различии значений однотипных параметров

объектов и больших ожидаемых погрешностях

X exp f- j ( ; ⁽ n i» k , !\2j ( i k ) v r = 1                    / L r = 1

w ;

E ⁽ n

¹ i

^{( n} ) к

.                           X

2 " t ( i⁽ ?) 2 r = 1

измерений могут быть достигнуты такие же зна-

чения вероятности (9), что и для близких зна-

чений

E ^{( n} ) ^; i

и

^;( 1

, i = 1 . I , n >  1 при малых

СКО i⁽ n ) и c ( 1 n ) . Множитель

nn

X exp - j^ ) -$ <^r ) ) /₂ j ( i⁽ r ))

_V r = 1                     / L r = 1

. 2« j [ ( i ( r ) ) ² + ( a⁽ r ) ) ²

V r = 1 ^L

– условные плотности вероятности признаков идентификации пары объектов ( i , k ) , i = 1 . I , k = 1 . K I , n >  1.

Вследствие априорной неопределенности одно-

типных параметров при вычислении апостериорной вероятности гипотезы об отождествлении объектов, выявленных различными СМ, истинные значения Т kn ) , k = 1 . K j , n >  1 в (10)—(12)

в (14) увеличивает нормированные информационные потери [6] для измерений, выполненных с низкой точностью [6; 8].

Полагая равными значения априорной вероятности условия отождествлении каждого i -го объекта, i = 1 . 1 , с учетом (8)—(13) правило (7) представим в виде

заменяются оценками добия [6]:

максимального правдопо-

( i‘, k') = arg max P* f ;(n) i=1. I,     V k=1. KI

E ^{( n} ) |

^; i I ,

ll n )• k

( i ( n ) ) ^{- 2} + j ; ( ⁿ ^( i¹ ’* ’) i = 1

I

- 2

w ^{( n} )_ .

^Т k = 1

( i kn T2+ j ( i⁽ n ’) i = 1

при k = 1 J ;

j ; iⁿ ) - ( i⁽ n ^l) ^{- 2}

i=1________________________ j (i(nT2

i = 1

при k = J + 1 . K i .

- 2

Используя (10)–(13), несложно показать, что при отождествлении I объектов, выявленных первым СМ, с одним объектом, данные (сведения) о котором поступают от второго СМ, закон распределения признаков идентификации (10) имеет вид

где символ «*» означает, что условная вероятность (8) вычисляется при замене в (10) истинных значений признаков идентификации ^ kn ) их оценками максимального правдоподобия Т kⁿ ) , k = 1 . K_I , n >  1.

2. Анализ статистических характеристик отождествления объектов при априорной неопределенности признаков идентификации

Для анализа эффективности алгоритма (15) на основе имитационного моделирования потока значений однотипных параметров [8; 9] найдены статистические характеристики отождествления объектов по оценкам их координат ( n = 2):

; ⁽? = ix i ,    ; ( ² ) = y i , i = 1 . 1 ,

1^= x k ,    I k ²⁾= У k ,    k = 1 . K i .

Область Q

( 2 )

ограничена окружностью радиуса

R; при этом (9) имеет вид

P (xk, yk| xi,yi; q(2)) = xk+R yk+VR -(xk-xsi)

= ² J           J         w ( x k , y k\ x i , ^y i ) ^x    (17)

x k - R        y k x dyi dxi,   i = 1 ™I, k = 1 ™Ki,

распределение w

( ^x k , y k|

/-V             /-V I x i, У i)

в явном виде

может быть получено из (10)–(12) путем замены

переменных (16) с введением унифицированных обозначений:

( 1 )                    ( 2 )

& i = &  x ,    & i = &  y , i = 1 ™ I ,

^ ^{( 1 )}— ^      ^ ^{( 2 )}    ^

& k & x ,    & k    & y , ^k 1 ™ K I ^.

при равной точности оценки однотипных пара-

метров для всех I и K _I объектов.

Вероятность правильного отождествления объектов Р ₀ определялась как статистически

усредненное отношение числа правильно отождествленных целей к общему количеству выполненных отождествлений, вероятность ложной тревоги Р ₁ – как отношение математического ожидания ложно выполненных к общему количеству возможных ошибочных отождествлений [5; 9].

На рис. 1 приведены зависимости Р ₀ от плотности размещения объектов, выявленных первым СМ, p i в общей зоне ответственности СМ. Сплошной линией представлены результаты, полученные при R = 2 & , где & = ^& x + & ^ , & _x y = &  _x y = 0,1 км, а пунктирной линией — при R = 3,5 & ; вероятность ложной тревоги составляет 0,01.

Из зависимостей следует, что при R = 2 &  и указанных значениях & xy и &  xy увеличение плотности объектов с 0,5 км ^{- 2} до 2 км ^{- 2} приво-

дит к снижению вероятности правильного ото-

ждествления с 0,9 до 0,65. С увеличением R до 3,5 &  при p = 0,5 км ^{- 2} величина Р_о возрастает до 0,95, а при & _x y = & _x y = 0,2 км, R = 3,5 &  и p = ( 0,5 ...2 ) км ^{- 2} лежит в пределах 0,55 ... 0,8 при вероятности ложной тревоги, не превышающей 0,02.

Установлено, что при R <  2 &  вероятность правильного отождествления объектов даже

при значительных расстояниях между ними

ограничивается вероятностью попадания параметров идентификации в область ^ ( 2 ) . Поэтому

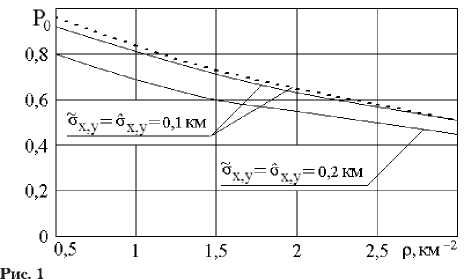
для достижения показателя Р 0 = 0,95...0,99 при Р ₁ = 0, 01 требуется высокая (не менее 0,1 км) точность местоопределения объектов [7; 9].

В частном случае отождествления объектов по оценкам координат (; x 1 ; г) 1 ) и ( x 1 ; y 1 = 0 ) при наличии вскрытых двумя СМ мешающих целей в

точках ( 5: 2 ; ^:y2 ) и ( x:

0; y 2 = 0 ) условная вероят-

ность группирования однотипных параметров (17)

ZX в предположении, что &

& + &,, —> 0, т. е. xy

значения ( гс 1 ; 0 ) и ( 0; 0 ) близки к истинным, ет вид [7]:

P ( x 1 ,0 1

P ( x 1,01

где

име-

•W xs 1,

•W x 2

y 1 ; ^ ( 2 ) )

= 1

—

f- R 2 1 ч 2 & ² >

, y 2 ; « ( 2 ) ) =

2 x c i 2 & ²

1     ^x k ^{+ R}     f

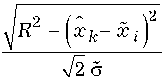
die i ,

a

2² erf ( a ) =        e t dt

\ n

x

– функция (интеграл) ошибок, а условная вероятность ситуации отождествления (8) определяется выражением [7]

P ( x 1 , 0 I

•w xs 1

r

, y / 1 ) = ^{1 -} exp

f- R 2

2 & ²

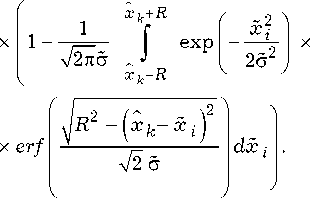
x

Как показано в [7], с увеличением расстояния между объектами xк с 3,3d до 4d при R/ d = 4 значение (21) повышается с 0,6 до 0,8, а за счет изменения R от 4d до 6d при x к ]6 = 3,3 — воз- растает с 0,6 до 0,9.

Заключение

Таким образом, с использованием критерия минимума среднего риска [4; 5] и оценок максимального правдоподобия однотипных параметров [6] выполнен синтез алгоритма многоальтернативного отождествления объектов совместно функционирующими СМ в условиях априорной неопределенности признаков идентификации [5]. Показано, что при равенстве нулю рисков принятия правильных решений и одинаковых информационных потерях для всех неправильных решений, а также равных значениях апостериорных вероятностей гипотез об отождествлении идентификации подлежат объекты с максимальной условной вероятностью ситуации отождествления. При этом априори неизвестные значения признаков идентификации, обусловленные в том числе их пропусками в различных СМ, требуется заменять оценками максимального правдоподобия.

Исследованы статистические характеристики эффективности отождествления целей по результатам независимых измерений их координат. Установлено, что вероятность правильного отождествления в совместно функционирующих СМ и сопутствующая ей вероятность ложной тревоги зависят от числа, плотности размещения и точности оценки однотипных параметров объектов, а также области возможных значений признаков идентификации [7], принадлежащих отождествляемым целям.