Многоцелевые проекты в задаче формирования программы развития нефтегазовой отрасли

Важнейшей частью технологии формирования комплексных программ регионального развития является технология комплексной оценки развития отрасли. В этой связи выделяется нефтегазовая отрасль, которая является локомотивом для всей экономики государства, способствует развитию других отраслей экономики, т. е., говоря о социально-экономическом эффекте от внедрения того или иного проекта, можно отметить значимое воздействие этой отрасли на социально-экономическое развития всей системы – как страны, так и ее отдельных регионов.

Отрасль здесь рассматривается как сложная социально-экономическая система и оценивается по ряду критериев [1, 2]. Задача заключается в построении комплексного критерия, наиболее верно отражающего степень достижения поставленных перед системой (в данном случае – отраслью) целей.

В настоящее время чаще всего используется многокритериальная оптимизация, при которой качество функционирования объекта определяется некоторым набором критериев оптимальности или эффективности функционирования [3, 4]. Настоящая статья является продолжением работы «Формирование интегральной оценки уровня инновационного развития отрасли», в которой рассмотрены многокритериальные задачи и предложен метод комплексного оценивания вариантов программы на основе матричных сверток. Рассматривалась нефтегазовая отрасль, в качестве существенных критериев, по которым проводилась комплексная оценка отрасли, выбраны следующие факторы: ВВП; добыча нефти и газового конденсата; привлечение иностранных инвестиций в нефтегазовый сектор; экспорт нефти, включая газовый конденсат. Дана постановка задачи оптимизации программы отраслевого развития как задачи достижения требуемого значения комплексной оценки варианта программы с заданными резервами направлений и минимальными затратами. Предложены алгоритмы ее решения на основе методов сетевого программирования.

В данной статье эти механизмы распространяем на так называемые многоцелевые проекты, которые дают эффект в несколько критериев [2].

1.    Постановка задачи

Рассмотрим случай, когда имеются многоцелевые проекты, то есть проекты, дающие эффект в несколько направлений (показателей). Например, увеличение экспорта нефти, безусловно, дает вклад и в увеличение ВВП; рост привлечений иностранных инвестиций дает вклад в увеличение добычи нефти и т. д.

Обозначим: Q – множество многоцелевых проектов, a ij – эффект, который дает многоцелевой проект j в направлении i. При сравнительно небольшом числе многоцелевых проектов эффектив-

Управление в социально-экономических системах

ным является метод рассмотрения всех вариантов вхождения многоцелевых проектов в программу с выбором из них наилучшего. Так, если число многоцелевых проектов q = 10, то число рассматриваемых вариантов равно 2q = 210 = 1024, что не представляет проблем. Поскольку при заданном множестве многоцелевых проектов, включенных в программу, задача сводится к рассмотренной в предыдущей работе, то алгоритм решения рассмотрим на примере для 2 показателей.

Пример 3 . Имеются восемь проектов, из которых 2 являются многоцелевыми. Данные о проектах приведены в табл. 1.

Таблица 1

i	1	2	3	4	5	6	7	8
a i1	6	4	5	3	6	0	0	0
a i2	0	0	0	5	4	7	5	3
c i	4	2	6	3	5	7	3	2

Примем значения показателей для направлений Y 1 = 6, Y 2 = 8, а граничные значения шкал

А 11 = 9, А 12 = 15, А 13 = 20, А 21 = 13, А 22 = 18, А 23 = 20.

Имеем Δ 11 = 3, Δ 12 = 9, Δ 13 = 14, Δ 21 = 5, Δ 22 = 10, Δ 23 = 12.

Поскольку имеются 2 многоцелевых проекта, то необходимо рассмотреть 22 = 4 варианта.

Вариант 1 . Ни один многоцелевой проект не входит в программу.

Решаем задачу для первого направления: минимизировать 4х 1 + 2х 2 + 6х 3 при ограничении 6х 1 + 4х 2 + 5х 3 ≥ 14; 9; 3.

Легко видеть, что для оценки 4 существует единственное решение х1 = х2 = х3 = 1 с затратами 15.

Для оценки 3 оптимальное решение х 1 = 1, х 2 = 1, х 3 = 0 с затратами 10.

Для оценки 2 оптимальное решение х 1 = 0, х 2 = 0, х 3 = 1 с затратами 5.

Решаем задачу для второго направления: минимизировать 7х₆ + 3х₇ + 2х₈ при ограничении 7х 6 + 5х 7 + 3х 8 ≥ 12; 10; 5.

Для оценки 4 оптимальное решение х 6 = 1, х 7 = 1, х 8 = 0 с затратами 10.

Для оценки 3 оптимальное решение х 6 = 1, х 7 = 0, х 8 = 1 с затратами 9.

Для оценки 2 оптимальное решение х 6 = 0, х 7 = 1, х 8 = 0 с затратами 3.

Вариант 2. Проект 5 входит в программу, а проект 6 не входит, корректируем значения Δ ij :

Δ 11 = –3, Δ 12 = 3, Δ 13 = 8, Δ 21 = 1, Δ 22 = 6, Δ 23 = 8.

Решаем задачу для первого направления: минимизировать 4х1 + 2х2 + 6х3.

При ограничении 6х 1 + 4х 2 + 5х 3 ≥ 8; 3; –3 для оценки 4 оптимальное решение х 1 = 1, х 2 = 1, х 3 = 0 с затратами 6.

Для оценки 3 оптимальное решение х 1 = 0, х 2 = 1, х 3 = 0 с затратами 2.

Для оценки 2 оптимальное решение х1 = х2 = х3 = 0 с затратами 0.

Решаем задачу для второго направления: минимизировать 7х 6 + 3х 7 + 2х 8 при ограничении 7х 6 + 5х 7 + 3х 8 ≥ 8; 6; 1.

Для оценки 4 оптимальное решение х 6 = 0, х 7 = 1, х 8 = 1 с затратами 5.

Для оценки 3 оптимальное решение х 6 = 0, х 7 = 1, х 8 = 1 с затратами 5.

Для оценки 2 оптимальное решение Х 6 = 0, х 7 = 0, х 8 = 1 с затратами 2.

Вариант 3 . Проект 5 не входит в программу, а проект 4 входит, корректируем значения Δ ij :

Δ 11 = 0, Δ 12 = 6, Δ 13 = 11, Δ 21 = 0, Δ 22 = 5, Δ 23 = 4.

Решаем задачу для первого направления: минимизировать 4х 1 + 2х 2 + 6х 3 при ограничении 6х 1 + 4х 2 + 5х 3 ≥ 11; 6; 0.

Для оценки 4 оптимальное решение х 1 = 1, х 2 = 0, х 3 = 1 с затратами 10.

Для оценки 3 оптимальное решение х 1 = 1, х 2 = 0, х 3 = 0 с затратами 4.

Для оценки 2 оптимальное решение х1 = х2 = х3 = 0 с затратами 0.

Решаем задачу для второго направления: минимизировать 7х₆ + 3х₇ + 2х₈ при ограничении 7х 6 + 5х 7 + 3х 8 ≥ 7; 5; 0.

Для оценки 4 оптимальное решение х 6 = 0, х 7 = 1, х 8 = 1 с затратами 5.

Для оценки 3 оптимальное решение х 6 = 0, х 7 = 1, х 8 = 0 с затратами 3.

Для оценки 2 оптимальное решение х 6 = 0, х 7 = 0, х 8 = 0 с затратами 0.

Бурков В.Н., Уандыкова М.К., Елеукулова А.Д.

Вариант 4 . Оба проекта 4 и 5 входят в программу, корректируем значения Δ ij :

Δ 11 = –6, Δ 12 = 0, Δ 13 = 5, Δ 21 = –4, Δ 22 = 1, Δ 23 = 3.

Решаем задачу для первого направления: минимизировать 4х₁ + 2х₂ + 6х₃ при ограничении 6х 1 + 4х 2 + 5х 3 ≥ 5; 0; –6.

Для оценки 4 оптимальное решение х 1 = 0, х 2 = 0, х 3 = 1 с затратами 6.

Для оценки 3 и 2 оптимальное решение х 1 = 0, х 2 = 0, х 3 = 0 с затратами 0.

Решаем задачу для второго направления: минимизировать 7х₆ + 3х₇ + 2х₈ при ограничении 7х 6 + 5х 7 + 3х 8 ≥ 3; 1; –4.

Для оценки 4 оптимальное решение х 6 = 0, х 7 = 0, х 8 = 1 с затратами 2.

Для оценки 3 оптимальное решение х 6 = 0, х 7 = 0, х 8 = 1 с затратами 2.

Для оценки 2 оптимальное решение х 6 = 0, х 7 = 0, х 8 = 0 с затратами 0.

Итак, мы получили 4 матрицы (S ij ) по одной для каждого из рассмотренных вариантов вхождения в программу многоцелевых проектов.

Вариант 1

Вариант 2

Таблица 2

J	1	2	3	4
1	0	5	10	15
2	0	3	9	10

Таблица 3

J	1	2	3	4
1	0	0	2	6
2	0	2	5	5

Вариант 3

Вариант 4

Таблица 4

J	1	2	3	4
1	0	0	4	10
2	0	0	3	5

Таблица 5

J	1	2	3	4
1	0	0	0	6
2	0	0	2	2

Рассмотрим систему комплексного оценивания. Поскольку направлений 2, то достаточно одной матрицы свертки. Возьмем, например, матрицу (рис. 1). Решаем задачу выбора оптимальной стратегии для всех 4 вариантов.

4	3; 6	3; 8	4; 10	4; 14
3	2; 4	3; 6	3; 8	3; 12
2	2; 1	2; 3	2; 5	3; 9
1	1; 0	1; 2	2; 4	2; 8
2 1	1	2	3	4

Рис. 1

Вариант 1 . Решение приведено в табл. 6. Результаты сведены в табл. 7.

Таблица 6

4	3; 10	3; 15	4; 20	4; 25
3	2; 9	3; 14	3; 19	3; 24
2	2; 3	2; 8	2; 13	3;18
1	1; 0	1; 5	2; 10	2; 15
2 1	1	2	3	4

Таблица 7

Оценка	1	2	3	4
Затраты	0	3	13	20

Управление в социально-экономических системах

Вариант 2 . Решение приведено в табл. 8. Результаты сведены в табл. 9.

Таблица 8

4	3; 5	3; 5	4; 7	4; 11
3	2; 5	3; 5	3; 7	3; 11
2	2; 2	2; 2	2; 4	3; 8
1	1; 0	1; 0	2; 2	2; 6
2 1	1	2	3	4

Таблица 9

Оценка	1	2	3	4
Затраты	0 + 5	2 + 5	5 + 5	7 + 5

Вариант 3 . Решение приведено в табл. 10. Результаты сведены в табл. 11.

Таблица 10

4	3; 5	3; 6	4; 9	4; 15
3	2; 3	3; 3	3; 7	3; 13
2	2; 0	2; 0	2; 4	3; 10
1	1; 0	1; 0	2; 4	2; 10
2 1	1	2	3	4

Таблица 11

Оценка	1	2	3	4
Затраты	0 + 3	0 + 3	3 + 3	9 + 3

Вариант 4 . Решение приведено в табл. 12. Результаты сведены в табл. 13.

Таблица 12

4	3; 2	3; 2	4; 2	4; 8
3	2; 2	3; 2	3; 2	3; 8
2	2; 0	2; 0	2; 0	3; 6
1	1; 0	1; 0	2; 0	2; 6
2 1	1	2	3	4

Таблица 13

Оценка	1	2	3	4
Затраты	0 + 8	0 + 8	2 + 8	2 + 8

Сравнивая все 4 варианта, определяем оптимальную стратегию.

Для оценки 2 оптимальная стратегия определяется вариантами 1 или 3. Для варианта 1 эта стратегия (1; 2), то есть достижение по показателю 2 оценки 2 при сохранении оценки 1 по показателю 1. Аналогичная стратегия для варианта 3. Для оценки 3 оптимальная стратегия определяется третьим вариантом. Это та же стратегия (1; 2), то есть достижение оценки 2 по показателю 2, сохранением оценки 1 по показателю 1. Для оценки 4 оптимальная стратегия определяется четвертым вариантом. Эта стратегия (3; 4), то есть достижение по показанию 1 оценки 3, а по показанию 2 оценки 4.

В соответствии с полученными стратегиями определяются программы для каждой поставленной цели. Если цель заключается в достижении оценки 2, то оптимальная программа включает проект 7. Если цель заключается в достижении оценки 3, то оптимальная программа включает проекты 4, 7 и 8.

Бурков В.Н., Уандыкова М.К., Елеукулова А.Д.

2.    Метод ветвей и границ

При большом числе многоцелевых проектов метод перебора всех вариантов их вхождения в программу становится неэффективным [1–4]. Рассмотрим применение для решения задачи метода ветвей и границ [5] с получением оценок на основе метода сетевого программирования [6]. Для получения нижних оценок затрат разделим затраты многоцелевого проекта произвольным образом на несколько частей, число которых равно числу направлений, в которые дает вклад данный проект. При таком делении для каждого показателя получаем множество одноцелевых проектов и можно применить алгоритм пункта 3. В теории сетевого программирования показано, что полученное оптимальное решение дает оценку снизу затрат на достижение той или иной величины интегральной оценки [7, 9]. Более того, если в получаемом решении каждый многоцелевой проект либо входит в программу по каждому направлению, в которое он дает эффект, либо не входит ни в одно из таких направлений, то это решение является оптимальным. На основе полученной нижней оценки можно применить метод ветвей и границ [8]. Поскольку метод ветвей и границ достаточно хорошо известен, алгоритм рассмотрим на данном примере 3.

Пример 4 . Поскольку имеются два многоцелевых проекта 4 и 5, то разделим затраты С 4 и С 5 на две части произвольным образом. Возьмем, например, С 41 = 2, С 42 = 1,С 51 = 2,С 52 = 3 получаем две задачи по одной для каждого направления.

Задача 1 (первое направление): минимизирование 4х 1 + 2х 2 + 6х 3 + 2х 4 + 2х 5 при ограничении 6х 1 + 4х 2 + 5х 3 + 3х 4 + 6х 5 ≥ 14; 9; 3.

Применяем метод дихотомического программирования, взяв структуру дихотомического представления (рис. 2) [10, 11].

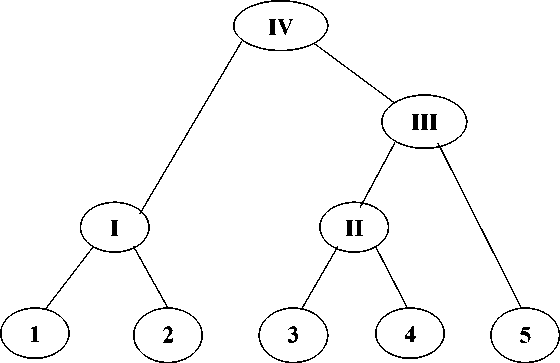
Рис. 2

Первый шаг. Рассматриваем проекты I и II. Результаты представлены в табл. 14.

Второй шаг. Рассматриваем проекты III и IV. Результаты представлены в табл. 15.

Таблица 14

Обобщенный проект I

Вариант	0	1	2	3
Эффект	0	4	6	10
Затраты	0	2	4	6

Таблица 15

Обобщенный проект II

Вариант	0	1	2	3
Эффект	0	3	5	8
Затраты	0	2	6	8

Третий шаг. Рассматриваем объединенный проект II и проект V. Результаты представлены в табл. 16.

Четвертый шаг. Рассматриваем объединенные проекты I и III. Решения приведены в табл. 17.

Управление в социально-экономических системах

Таблица 16

Обобщенный проект III

Вариант	0	1	2	3	4
Эффект	0	6	9	11	14
Затраты	0	2	4	8	10

Таблица 17

3	10; 6	16; 8	19; 10	21; 14	24; 16
2	6; 14	12; 6	15; 8	17; 12	20; 14
1	4; 2	10; 4	13; 6	15; 10	18; 12
0	0; 0	6; 2	9; 4	11; 8	14; 10
I III	0	1	2	3	4

Для Δ ₁₃ = 14 оптимальное решение определяется клеткой (16; 8) или (15; 8) с затратами 8.

Для Δ ₁₂ = 9 оптимальное решение определяется клеткой (10; 4) с затратами 4.

Для Δ 11 = 3 оптимальное решение определяется клеткой (6; 2) или (4; 2) с затратами 2.

Задача 2 (второе направление): минимизировать 1х₄ + 3х₅ + 7х₆ + 3х₇ + 2х₈ при ограничении 5х 4 + 4х 5 + 7х 6 + 5х 7 + 3х 8 ≥ 12; 10; 5.

Возьмем структуру дихотомического представления в виде рис. 2, заменив проекты 1, 2, 3 на 6, 7, 8 соответственно.

Первый шаг. Рассмотрим проекты 6 и 7. Результаты представлены в табл. 18.

Второй шаг. Рассматриваем проекты 4 и 8. Результаты представлены в табл. 19.

Таблица 19

Таблица 18

Обобщенный проект I

Обобщенный проект II

Вариант	0	1	2	3		Вариант	0	1	2
Эффект	0	5	7	12		Эффект	0	5	8
Затраты	0	3	7	10		Затраты	0	1	3

Третий шаг. Рассматриваем обобщенный проект II и проект 5. Результаты представлены в табл. 20.

Четвертый шаг. Рассматриваем объединенные проекты I и III. Решения приведены в табл. 21.

Таблица 20

Обобщенный проект III

Вариант	0	1	2	3	4
Эффект	0	5	8	9	12
Затраты	0	1	3	4	6

Таблица 21

3	12; 10	17; 11	20; 13	21; 14	24; 16
2	7; 7	12; 8	15; 10	16; 11	19; 13
1	5; 3	10; 4	13; 6	14; 7	17; 9
0	0; 0	5; 1	8; 3	9; 14	12; 6
I III	0	1	2	3	4

Для Δ 23 = 12 оптимальное решение определяется клеткой (12; 6) с затратами 6.

Для Δ 22 = 10 оптимальное решение определяется клеткой (10; 4) с затратами 4.

Для Δ ₂₁ = 5 оптимальное решение определяется клеткой (5; 1) с затратами 1.

Получив матрицу затрат (S ij ), рассмотрим систему комплексного оценивания в качестве которой, как и в примере 3, возьмем матрицу (см. рис. 1).

Рассмотрим задачу достижения оценки 3 (хорошо). Оптимальной стратегии соответствуют две клетки (3; 6) с затратами 6. Рассмотрим первое решение, то есть достижение оценки 1 по пер-

Бурков В.Н., Уандыкова М.К., Елеукулова А.Д.

вому направлению и оценки 4 по второму, что соответствует включению в программу проектов 4, 5 и 8 по второму направлению и ни одного проекта по первому направлению. Рассмотрим второе решение, то есть достижение оценки 2 по первому направлению и оценки 3 по второму. Это соответствует включению в программу либо проекта 2, либо проекта 5.

Оценке 3 по второму направлению соответствует включение в программу проектов 7 и 4.

Заметим теперь, что ни в первом, ни во втором решении не выполняется условие, что либо проект входит в программу в обоих направлениях, либо не входит ни в один из них. Поэтому полученные решения определяют только нижнюю оценку затрат, которая равна 6.

Применяем метод ветвей и границ [12]. Для ветвления выберем многоцелевой проект 4. Делим множество всех решений на два подмножества. В первом проект 4 входит в программу, а во втором не входит.

Оценка первого подмножества. Поскольку проект 4 входит в программу, то корректируем значения Δij, вычитая из них эффекты a41 = 3 и а42 = 5, соответственно. Имеем Δ11 = 0, Δ12 = 6, Δ13 = 11, Δ21 = 0, Δ22 = 5, Δ23 = 7.

С новыми значениями повторяем решения задач 1 и 2.

Решение задачи 1 : минимизировать 4х₁ + 2х₂ + 6х₃ + 2х₅ при ограничении 6х 1 + 4х 2 + 5х 3 + 6х 5 ≥ 11; 6; 0.

Решение можно получить сразу. Для получения оценки 4 в программу включаются проекты 3 и 5 с затратами 8.

Для получения оценки 3 в программу включается проект 5 с затратами 2.

Для получения оценки 2 в программу не включается ни один из оставшихся проектов (затраты 0).

Решение задачи 2 : минимизировать 3х 5 + 7х 6 + 3х 7 + 2х 8 при ограничении

4х 5 + 7х 6 + 5х 7 + 3х 8 ≥ 7; 5; 0.

Определяем решение задач.

Для получения оценки 4 в программу включаются либо проекты 5 и 8, либо проекты 7 и 8

с затратами 5.

Для получения оценки 3 в программу включается проект 7 с затратами 3.

Для получения оценки 2 в программу не включается ни один из оставшихся проектов (затраты 0).

Получив данные о затратах (S ij ) определяем оптимальную стратегию (рис. 3).

4	3; 5	3; 5	4; 7	4; 13
3	2; 3	3; 3	3; 5	3; 11
2	2; 0	2; 0	2; 2	3; 8
1	1; 0	1; 0	2; 2	2; 8
2 1	1	2	3	4

Рис. 3

Оптимальное решение определяется клеткой (3; 3) ему соответствует включение в программу проекта 7 по второму направлению. Окончательно получаем, что в программу включаются проекты 4 и 7 с суммарными затратами 6. Полученное решение является оптимальным, поскольку нижняя оценка затрат, полученная на предыдущем шаге, равна 6.

Заключение

В статье рассмотрены многоцелевые проекты, которые дают эффект в несколько направлений. Дана методика комплексного оценивания таких проектов. Рассмотрены задачи формирования программы развития отрасли, обеспечивающей требуемое значение комплексной оценки с минимальными затратами на основе метода ветвей и границ и оптимизации на основе метода сетевого программирования. Данная технология применима и для формирования программ регионального развития.

Статья подготовлена по результатам исследований, выполненных за счет бюджетных средств по государственному заданию Финуниверситета 2017 года.