Многократное рассеяние ультразвуковых волн на системе пространственных дефектов канонической формы (теория и эксперимент)
Автор: Боев Николай Васильевич, Эль-Мораби Халед Мохамед, Вдовин Владимир Александрович, Зотов Владимир Михайлович
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Физико-математические науки
Статья в выпуске: 3 (64) т.12, 2012 года.
Бесплатный доступ
Описана детерминированная модель распределения дефектов. Проведён сравнительный анализ теоретического расчёта и экспериментальных данных многократного отражения ультразвуковых волн на системе трёх цилиндрических дефектов, находящихся в упругом теле конечных размеров.
Рассеяние, ультразвуковые волны, пространственные дефекты, высокочастотная дифракция
Короткий адрес: https://sciup.org/14249839
IDR: 14249839 | УДК: 539.3
Текст научной статьи Многократное рассеяние ультразвуковых волн на системе пространственных дефектов канонической формы (теория и эксперимент)
Введение. При сканировании скопления дефектов в упругих телах раздельно-совмещенными ультразвуковыми датчиками [1] информация об их местоположении и форме может быть получена на основе характеристик однократно и многократно переотраженных волн. Полное исследование такой задачи возможно только на основе решения трехмерной задачи высокочастотной дифракции ультразвуковых волн. С учетом применяемых частот в ультразвуковом неразрушающем контроле (УЗНК) материалов теоретическое исследование трехмерных задач многократного рассеяния упругих волн может быть проведено в рамках геометрической теории дифракции [2,3]. Особый интерес представляет исследование задач высокочастотной дифракции в рамках стохастической модели распределения дефектов в теле конечных размеров. Однако в качестве начальных вариантов изучения этой проблемы естественным является ее изучение в рамках детерминированных моделей распределения дефектов канонической формы.
Детерминированная модель и экспериментальные измерения. Модель реализована в лабораторном макете, который в качестве тела конечных размеров использует стальной образец в форме прямого параллелепипеда, толщина образца 40 мм, высота 78 мм, длина 300 мм. На расстоянии Н от верхней грани, на которой располагается датчик продольных ультразвуковых волн (УЗ) диаметром 30 мм и частотой 2,5 МГц, по дуге окружности радиусом R просверлены три одинаковых соосных цилиндрических отверстия радиусом г с образующими перпендикулярными боковыми стенками. Схема образца с расположением отверстий и датчика приведена на рис.1. Для проведения эксперимента используется дефектоскоп-приставка «ЭВУД-ПК» (в дальнейшем дефектоскоп) общего назначения по ГОСТ 23049-94. Он предназначен для УЗ контроля продукции на наличие дефектов типа нарушения сплошности и однородности металлов. Дефектоскоп работает совместно с IBM компьютером.
Лучевое решение задачи. Расположение цилиндрических отверстий в образце и ультразвукового датчика продольной волны позволяют измерять амплитуду перемещений в обратно отраженных волнах от поверхностей полостей в продольных волнах, в двукратно отраженных от дефектов 1 и 3 волнах, в трехкратно отраженных волнах от всех трех препятствий. Траектории указанных лучей приведены на рис.1. Заметим, что эти траектории представляют собой ломаные линии, лежащие в одной плоскости. Общие случаи однократного и многократного отражения продольной волны от поверхностей, находящихся в упругой среде, получены в работах [3, 4]. Явные выражения перемещений в отраженных волнах получены в рамках геометрической теории ди-
Работа выполнена при поддержке Российского фонда фундаментальных исследований (10-01-00557а).
фракции [5] на основе модификации физической теории дифракции Кирхгофа [6] асимптотиче'
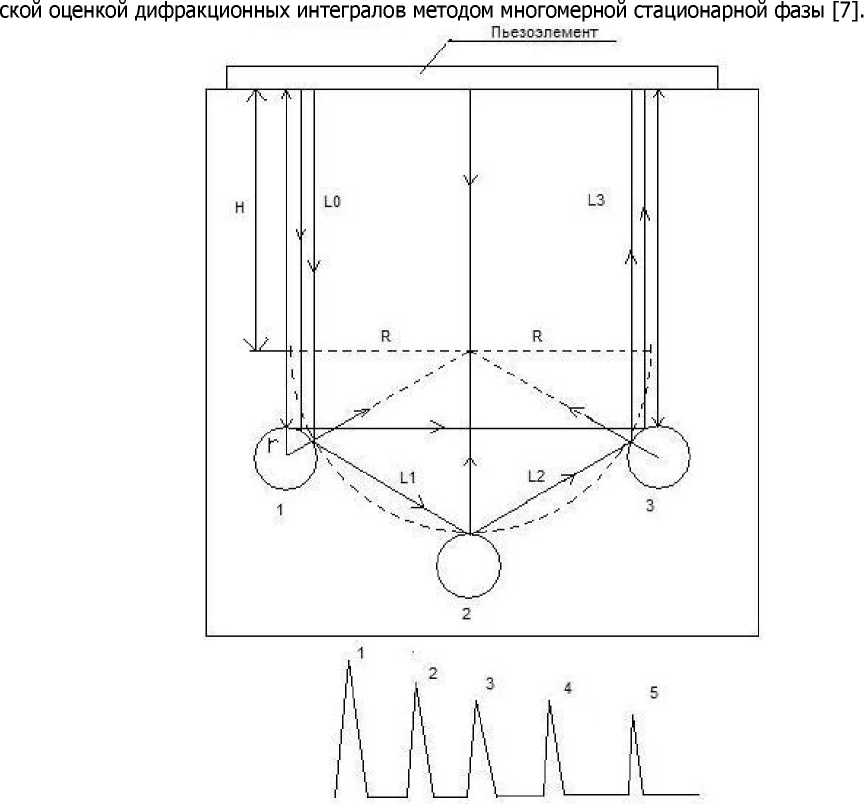
Рис.1. Схема образца с датчиком и осциллограмма с экрана дефектоскопа: 1 — зондирующий импульс; 2 — импульс, отражённый от отверстия 1 (импульс, отражённый от отверстия 5 по времени совпадает с импульсом, отражённым от отверстия 2); 3 — импульс, отражённый от отверстия 2; 4 — импульс, отражённый от отверстия 1 и переотражённый отверстием 3, 5 — импульс, отражённый от отверстия 1 и переотражённый отверстиями 2 и 3
Выпишем эти формулы для продольных перемещений ир в случаях однократного, двукратного, трехкратного отражения волны.
Случай однократного отражения:
«™ = Z-vW„(y )ехр ik, (/,+£,) + ^6* + 2)
Z = ^L0^ L^ ^IL^L^Lq^ L^^IHceos" у ^ksxxv y^cos"Yy ^МЗ^К ; (1)
L0=\x0-y\, Д =| У - x |;
8 = 0^4^'.
Здесь *0 - точка, в которой помещен источник продольной волны, вызванной единичной силой Qqe imt; х - точка приема волны; кр = Ю1СРЛ8= ^/с,- cP^cs - волновые числа и скорости соответственно продольной и поперечных волн; со - частота колебаний; Ц - модуль
б тт / * \ сдвига;
^№ v /" коэффициент р — р отражения (продольной волны в продольную);
— kxk^ - гауссова кривизна; Нс — ( k^+k^f 2
- средняя кривизна поверхности в
точке зеркального отражения У ; к - кривизна нормального сечения поверхности отражателя плоскостью луча ^д — У — х- Кривизна к определяется формулой Эйлера к - к enq 2 гл 4- к qin 2 гл ~ COS « . ~ COS (3
к -KXCOS
Формула (1) дает главный член асимптотики продольных перемещений при kpL0 »1, кр Д »1, кр Rx»\, кр R2 » 1, где ^ и R2 - главные радиусы кривизны поверхности в точке зеркального отражения у .
Угол У- это угол между направлением ^° = {-COSCZ,-COS (3, -cosy} падения и отражения продольной волны и нормалью к поверхности в точке у в локальной декартовой системе координат.
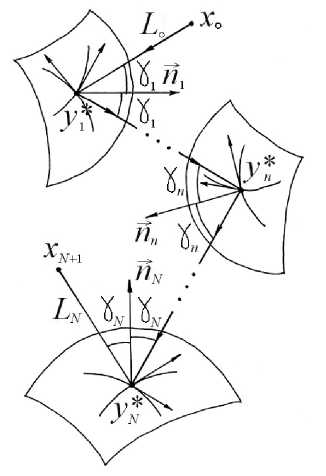
Рис.2. N-кратное отражение продольной волны вдоль луча ^о — Ут — Уз — ■•■— Ум — xn+i от граничных поверхностей N полостей, находящихся в упругой среде
Случай двукратного (N=2) и трехкратного (Л^=3) отражения (рис.2):
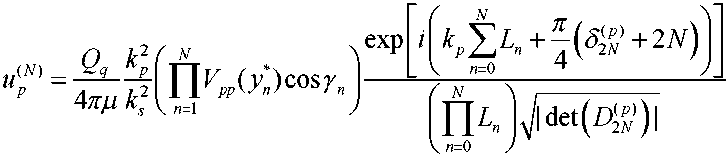
Здесь 5$ = signB^ - разность между числом положительных и отрицательных собственных значений матрицы Гессе -(^у), /,у = 1,2,...,27V (N=2,7V=3), которая является сим метричной со следующими ненулевыми элементами dijr,i диагональные элементы ^ = 1,2,3 и = 1,2 и = 1,2 и = 1,2 Здесь Цп\к^ (и=1,2,3) - главные кривизны поверхностей, a injn1k» - орты локальной декартовой системы координат, определяемой касательными к главным линиям кривизны и нормалям к поверхностям дефектов в точках зеркального отражения у*,и = 1,2,3 (см. рис.2). Координаты ортов заданы в некоторой глобальной декартовой системе координат, qn - направление падения волны в точке у*. Выше выписаны элементы матрицы Гессе D^ в случае трехкратного отражения волны. Для случая двукратного отражения элементы матрицы Гессе D^ =(^ ) (i,j=l,2,3,4) находятся в левом верхнем углу матрицы . Получим из общих формул (1) и (2) явные выражения для амплитуды перемещений, принимаемой датчиком (см. рис.1) продольной волны. Во всех случаях к^ = 1/г, kf = О, Х(!) = к^ = 0, i = 1,2,3 . 1. Обратное однократное отражение (см. рис.1): у = 0,Яс=0,5г,^=-1; а) от каждой из полостей 1 и 3 (первый отраженный импульс): Т - Т - 14 _Т R 01 2 2 Р / б) от полости 2 (второй отраженный импульс): L0=L,=H+R, и^=В 77 V Г,=Г2=р L0=Li = H+—*. L,=L,=R; C = R]1V, Сравнительный анализ. Измерения проведены на стальном образце. Скорости продольных и поперечных волн в стали соответственно равны с =5850 м/с, cs =3260 м/с. При частоте, излучаемой продольной волной 2,5 МГц, ее длина составляет 2,34 мм. Приведем, например, сравнение теоретических расчетов и результатов экспериментальных измерений амплитуды в обратно отраженных волнах от полостей 1 и 3 и в двукратно отраженной волне последовательно от дефектов 1 и 3. В результате эксперимента получены следующие значения амплитуды перемещений в отраженных волнах: амплитуда перемещений и^ в обратной однократно отраженной волне от де фекта I (см. рис.1) составляет 60,5 дБ; амплитуда перемещений и^р в двукратно отраженной волне последовательно от дефектов I и II составляет 29,5 дБ. Разность между этими значениями составляет 31 дБ. При этих данных отношение и^-1 /и^ = 35. Теоретические расчеты амплитуд и^ и //^'3' основывались на аналитических выражениях (3) и (4). При этом для отношения и^ ]и^ получено выражение = 51,20; Lo =48,94 мм, Д =12,88 мм, Н + 0,5(Л + г) = 50 мм, Урр =0,36 6z = l + Z1/Z0, b = 242Ljr. Расхождение для отношений амплитуд перемещений в обратно отраженной и двукратно отраженной волне экспериментальных измерений и теоретических расчетов составляет 3 дБ. С учетом того, что стальной образец изготовлен с погрешностями и излучаемая датчиком волна не является плоской, а отношение длины волны (2,34 мм) к диаметру полости (3 мм) не является малым, что не в полной мере соответствует лучевой теории, полученный результат является вполне удовлетворительным. Заключение. Используемые в УЗНК основные частоты зондирующих импульсов 2,5-10 МГц позволяют применять для тел ограниченных размеров аналитические выражения геометрической теории дифракции высокочастотных упругих волн, полученные для бесконечной среды, содержащей препятствия.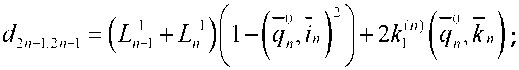
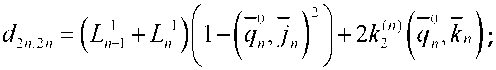
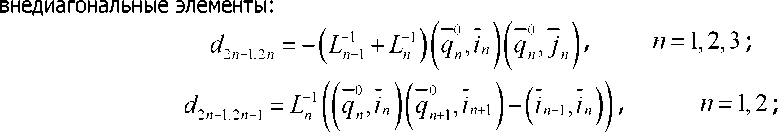
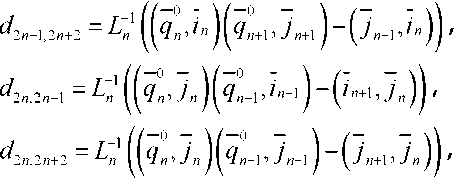
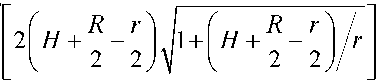
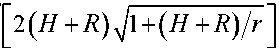
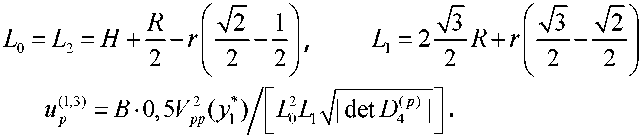
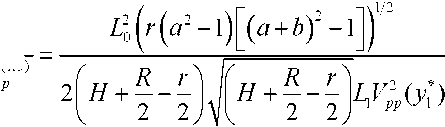
Список литературы Многократное рассеяние ультразвуковых волн на системе пространственных дефектов канонической формы (теория и эксперимент)
- Ермолов И.Н. Теория и практика ультразвукового контроля/И.Н. Ермолов. -М.: Машиностроение, 1981. -240 с.
- Боев Н.В. Коротковолновая дифракция на телах, ограниченных произвольной гладкой поверхностью/Н.В. Боев, М.А. Сумбатян//Докл. РАН. -2003. -Т.392, -№5. -С. 614-617.
- Боев Н.В. Метод граничных интегральных уравнений в задачах коротковолновой дифракции/Н.В. Боев, И.И. Ворович, М.А. Сумбатян//Изв. РАН. МТТ. -1992. -№5. -С.38-42.
- Боев Н.В. Рассеяние высокочастотных волн на поверхностях в сплошных средах с учетом переотражений//Акуст. журн. -2004. -Т.50. -№6. -С.756-761.
- Хенл Х. Теория дифракции/Х. Хенл, Л. Мауэ, К. Вестпфаль. -М.: Мир, 1964. -428 с.
- Боровиков В.А. Геометрическая теория дифракции/В.А. Боровиков, Б.Е. Кинбер. -М.: Связь, 1978. -248 с.
- Федорюк М.В. Метод перевала/М.В. Федорюк. -М.: Наука, 1977. -368 с.


