Многокритериальная модель планирования водно-энергетических режимов Новосибирской ГЭС

1.    ВВЕДЕНИЕ. ПОСТАНОВКА ЗАДАЧИ

Новосибирская ГЭС входит в единую энергетическую систему Сибири и является одним из основных крупных технических объектов г. Новосибирска. Изначально ГЭС была построена исключительно с энергетической целью, однако усиление антропогенных процессов привело к смене приоритетов водопользования, а развитие ОЭС Сибири снизило энергетическое значение Новосибирской ГЭС. В настоящее время водные запасы водохранилища используются сложившимся водохозяйственным комплексом: водоснабжение, водный транспорт, сельское и рыбное хозяйство, энергетика.

Периоды экстремального маловодья ставят под угрозу нормальную работу объектов жизнеобеспечения населенных пунктов и промышленных предприятий Новосибирской области и Алтайского края. Многоводные периоды приводят к затоплениям населенных пунктов и сопровождаются весьма сложными и чрезвычайными ситуациями. В связи с этим возникает сложная задача урегулирования интересов различных участников водохозяйственного комплекса для оптимального использования водных ресурсов.

В соответствии с Водным кодексом решения по управлению режимами принимаются территориальными подразделениями Федерального агентства водных ресурсов, при этом учитыва ются требования водопользователей, указан-

энергетический режим, ГЭС.

ные в Правилах использования водных ресурсов (далее - ПИВР). Стоит отметить, что при выборе режима управления речным стоком, а также при его оценке нельзя ограничиваться только экономической выгодой от дополнительной выработки электроэнергии. Перед эксплуатирующей организацией стоят такие задачи как: безопасность гидротехнических сооружений, оборудования и людей, безопасных попусков половодья, определяемых правилами технической эксплуатации. В этих условиях актуальной становится задача нахождения оптимального режима при выполнении ограничений всех водопользователей.

Задача планирования водно-энергетического режима ГЭС в весенне-летний период (апрель-июль) является наиболее сложной, т.к. именно в это период происходит постепенное наполнение водохранилища за счет притока воды к створу гидроузла до максимально возможного уровня. Задача планирования может быть решена на основе использования различных математических методов: календарных, имитационных, оптимизационных или их комплексного применения.

В настоящее время на Новосибирской ГЭС задача водно-энергетического планирования режимов решается с помощью имитационного моделирования. Основой такого моделирования является имитационный эксперимент, предполагающий получение некоторых выходных характеристик изучаемого объекта при задании определенных входных воздействий на объект и имитации процесса функционирования объекта во времени. Оптимальный режим ГЭС выбирается на базе имитационного эксперимента, в ходе которого специалист варьирует режимы расчета

и значения исходных параметров и определяет близкое к оптимальному управление. Основной недостаток метода имитационного моделирования заключается в том, что эффективность полученного решения во многом зависит от опыта и интуиции специалиста, вследствие чего, решение не является ни глобально, ни локально оптимальным в математическом смысле. Кроме того, метод трудоемок, его применение требует значительных временных затрат.

Одним из перспективных направлений представляется постановка и решение задачи планирования водно-энергетического режима работы ГЭС как оптимизационной задачи с использованием аппарата математического программирования.

Оптимизационному подходу к решению задачи планирования водно-энергетических режимов посвящено достаточно много работ [1-4]. Однако, в литературе, как правило, модели планирования описаны в общем виде, без привязки к конкретной ситуации. Кроме того, далеко не всегда приводятся результаты вычислительных экспериментов и сведения о практическом применении моделей. Также следует отметить, что каждая ГЭС имеет свои особенности, которые должны быть учтены в модели для получения адекватных результатов решения задачи планирования режимов.

Оптимизационная задача сводится к нахождению наилучшего варианта режима работы ГЭС из всех возможных в соответствии с заданным критерием (критериями) оптимальности при выполнении комплекса ограничений (водно-энергетических, морфометрических, режимных, управленческих, ограничений со стороны водопользователей и других). В данном исследовании задача планирования решается в многокритериальной постановке, в качестве критерия оптимальности выступает максимизация напора гидроустановки и минимизация суммарного расхода за период планирования. Такая стратегия управления приводит к увеличению выработки электроэнергии при обеспечении условий работы неэнергетических водопользователей.

Исходные данные для моделирования были предоставлены Новосибирским отделением ОАО «РусГидро».

2.    МОДЕЛЬ ПЛАНИРОВАНИЯ РЕЖИМОВ РАБОТЫ ГЭС

В основе модели планирования лежит уравнение водного баланса, которое описывает изменение объема водохранилища за период планирования (приток в водохранилище минус суммарный расход равен изменению объема водохранилища за период планирования). В модели могут использоваться разные критерии оптимальности или их комбинация, т.е. задача планирования может быть формализована и решена как однокритериальная или многокритериальная в зависимости от целей планирования. Также модель включает комплекс ограничений, которые можно разделить на следующие основные группы:

• -    технические, определяемые характеристиками гидрообъекта (максимальные расходы воды через турбины ГЭС и водосливную плотину, номинальная мощность и др.);

• -    управленческие, определяемые характеристиками водохранилища, Правилами использования водных ресурсов (ПИВР), диспетчерскими требованиями;

• -    сезонные (режим наполнения водохранилища в летний период, попуски на навигацию и др.);

• -    экологические и водохозяйственные, включающие минимизацию ущербов и рисков (исключение ситуаций переполнения верхнего бьефа, затопления нижнего бьефа и др.).

Подробнее рассмотрим один из вариантов оптимизационной модели. Модель позволяет определить оптимальный водно-энергетический режим Новосибирской ГЭС в период наполнения водохранилища (весенне-летний период, 12 декад с апреля по июль) в соответствии с заданными критериями. В модели используется два критерия оптимальности, а именно, максимизация суммарного напора и минимизация суммарного расхода за период планирования.

В качестве исходных данных в модели используется следующая информация:

• -    прогнозный объем притока к створу гидроузла за i -ую декаду с учетом доверительного интервала, т.е. p i ± A i , i = 1, N ;

• -    уровень верхнего бьефа на 1 апреля;

• -    расчетный перепад на СУР (сороудерживающим решеткам) по декадам;

• -    зимний коэффициент по декадам;

• - минимальные и максимальные значения параметров и переменных, обусловленные ПИВР и морфометрическими характеристиками водохранилища.

Приведем описание исходных данных:

z 0 = 108,5 - уровень верхнего бьефа на 1 апреля, м;

z min = 108,5 - минимальный уровень верхнего бьефа (отметка УМО), м;

z max = 113,5 — максимальный уровень верхнего бьефа (отметка НПУ), м;

N=12 - количество рассматриваемых периодов (декад);     ___

P m = ( Р ? ), i = 1, N — приток к створу гидроузла ГЭС среднедекадный (апрель-июль), м³/с;

P k = ( p i ), i = 1, N - приток к створу ГЭС среднедекадный (апрель-июль), км³;

Pk = к • Pm, где K = (ki), i = 1, N - коэффициент перевода расхода притока в м3/с в объем притока, км 3;

k i = t i • 24 • 3600 /10⁹ , где t i - количество дней в i -ом периоде (де каде);

S = ( s i ), i = 1, N - перепад на СУР за i -ый период, м;

h min = 13 - минимальный допустимый напор гидроустановки (нетто), м;

h max = 20 - максимальный допустимый напор гидроуст ан овки (нетто), м;

q max i , i = 1, N - максимальный суммарный расход за i -у ю д екаду, м³/с;

q min . , i = 1, N - минимальный суммарный расход за i -ую декаду, м³/с.

Переменные м одели:

Q = ( q i ), i = 1, N - суммарный расход за i -ый период, м³/с;

Z“ = ( z “ ), i = 1, N - уровень верхнего бьефа за i -ый период, м;

На основе значений переменных рассчитываются производные характеристики режима работы ГЭС, значения которых также выдаются на выходе модели:

Z d = ( z d ), i = 1, N - уровень нижнего бьефа за i -ый период, м;

H = ( h i ), i = 1, N - напор гидроустановки в i -ом периоде (нетто), м.

В модели используется также морфометрическая информация:

Зависимость статического объема водохранилища от уровня верхнего бьефа:

V = f ( Z u ) = 885,98 • Z u - 91924,89.    (1)

Коэффициенты модели оценены по результатам натурных измерений статического объема водохранилища и соответствующего ему уровня верхнего бьефа. В данном исследовании была использована линейная модель аппроксимации для упрощения оптимизационной модели и сведения ее к линейному виду.

Зависимость уровня воды в нижнем бьефе от суммарного расхода также описывается линейной моделью:

Z⁴ = f ( Q ) = 0,8•Ю ^{- 3} • Z⁴ + 93,05.       (2)

Коэффициенты функции Z d = f ( Q ) оценены по результатам натурных измерений суммарного расхода воды и соответствующего ему уровня нижнего бьефа.

В модели используется два критерия оптимальности, первый из которых реализует оптимизацию по напору:

N

C = X h i ^ max,           (3)

i = 1

а второй критерий по суммарному расходу:

N c2 =Z9i^ min.           (4)

i = 1

Для сведения задачи к однокритериальной выполнена нормализация и свертка критериев. Целевая функция модели минимизирует суммарные потери по критериям с учетом весовых коэффициентов и имеет вид:

C = c ₁ £ | h ^mx - h | + c ₂ £ | q i - q ^max i | ^ min, (5)

i=1 \ hmax hmin J      i=1 \ qmax i qmin i J где c1 и c2 – весовые коэффициенты, определяющие вклад в целевую функцию каждого из критериев в долях единицы.

Опишем ограничения модели.

В основе модели лежит уравнение водного баланса: разница между объемом притока воды к створу гидроузла и суммарным расходом воды за i -ый период равна изменению объема водохранилища за i -ый период:

P k — k i • Q i = d i , i = 1, N .             ⁽⁶⁾

Изменение объема водохранилища описывается как разница объемов водохранилища на конец и на начало i -го периода:

d_t = f ( z-^ — f ( z i ) = 885,98 • ( z “ + 1 - z i ), i = 0, ^ . (7)

Уровень нижнего бьефа в зависимости от суммарного расхода воды с учетом зимнего коэффициента за i -ый период, в м:

z d = f ( q i ) • k W , i = 1, N .             (8)

Напор за i -ый период определяется как разница между уровнями верхнего и нижнего бьефов и перепада на СУР:

h i = z i^u - z i - S i ,i = IT N .             (9)

Ограничение, не допускающее сработку водохранилища в период наполнения (уровень верхнего бьефа в i+1 -периоде не ниже уровня верхнего бьефа в i -ом период е):

z u + 1 - z u >  o, i = i; N .             (io)

Ограничение на равномерность суммарного расхода по периодам планирования (декады мая-июня, ограничение актуально для неэнергетических пользователей):

qi = qi+1, i = 4,7.

Уровень верхнего бьефа должен находиться в пределах отметок НПУ (113,5) и УМО (108,5) в i -ом периоде:

zmin < z“ < zmax, i = 1,N.

Ограничения на минимальный и максимальный допустимые напоры за i -ый период:

hmin < hi < hmax,i = 1, N•

Ограничения на суммарный расход за i -ый период:

qmin < qi < qmax, i = 1, N•

Построенная оптимизационная модель относится к классу задач линейного программирования и может быть решена с помощью симплекс- метода. В данном исследовании для решения задачи использовалась программа MSExcel -2013, модуль «Поиск решения» и MathLab.

Далее, на основании полученных в результате расчетов значений переменных модели, производится расчет остальных характеристик водно-энергетического режима, определяется Q* = (qi), i = 1, N - расход через турбины ГЭС за i-ый период, в м3/с и Qs = (qi), i = 1, N - холостой водосброс за i-ый период, м3/с.

Суммарный расход за i -ый период определяется как сумма расхода воды через турбины ГЭС и холостого водосброса:

q i = q i + q i , i = 1, N . ⁽¹⁵⁾

Значение q_i ^t определяется по таблице Q max = f ( H , Z d ) зависимости максимального расхода через турбины ГЭС от напора и уровня нижнего бьефа. В таблице для каждого значения напора в диапазоне H е [13; 20] и уровня нижнего бьефа в диапазоне Z d е [92; 97] с дискретностью (шагом) 0,1 приведен максимальный расход, который можно обеспечить при заданных характеристиках.

Мощность ГЭ С по периодам планирования W = ( w i ), i = 1, N определяется по таблице W = f ( H, Q ) зависимости мощности от напора гидроустановки и расхода через турбины ГЭС.

3. РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТОВ

С помощью разработанной оптимизационной модели было выполнено подекадное планирование водно-энергетического режима Новосибирской ГЭС на период с апреля по июль по данным 2017 г.

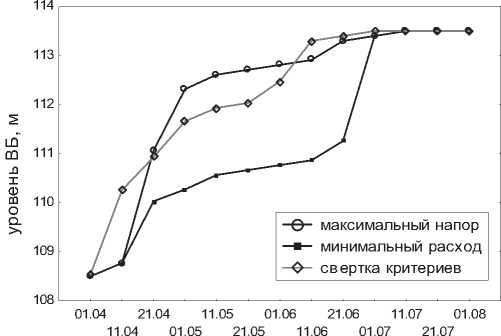
Были рассчитаны разные варианты режима, при задании разных сочетаний весовых коэффициентов c₁ и c₂ в целевой функции (5). На рис. 1 приведен график изменения уровня верхнего бьефа, построенный по результатам моделирования, соответственно при c₁ =1 и c₂ =0 (максимизация суммарного напора), c₁ =0 и c₂ =1 (минимизация суммарного расхода), c₁ =0,1 и c₂ =0,9 (компромиссное решение).

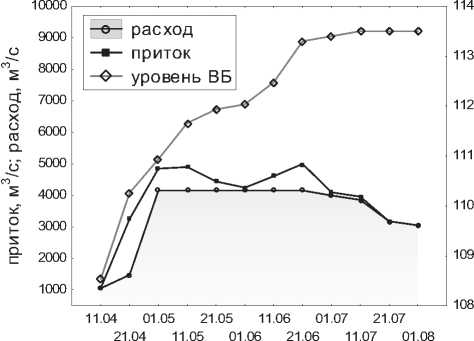
На рис. 2 приведен графики изменения водно-энергетических характеристик НГЭС на 2017 г., соответствующий компромиссному решению c₁ =0,1 и c₂ =0,9. На графике отображено

дата

Рис. 1. Уровень ВБ по периодам планирования на 2017 г. с учетом весовых коэффициентов ЦФ

дата

Рис. 2. Водно-энергетические характеристики режима НГЭС на 2017 г.

изменение уровня верхнего бьефа, расхода воды в нижний бьеф и прогнозного притока воды (среднее значение) по декадам.

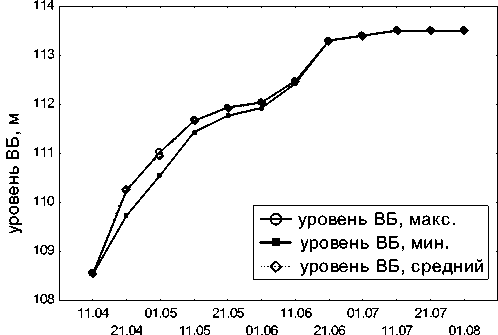
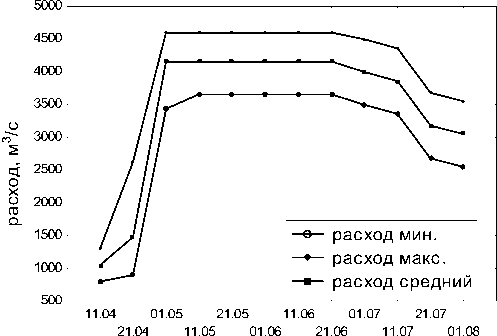
Учитывая, что на входе модели задается прогнозный объем притока с учетом доверительного интервала, расчеты режима выполняются для трех вариантов (минимальные, максимальные и средние значения прогнозного объема притока к створу ГЭС). На рис. 3-4 приведены графики изменения уровня верхнего бьефа и суммарного расхода по периодам планирования для трех вариантов исходных данных.

дата

Рис. 3. Уровень ВБ по периодам планирования на 2017 г. с учетом доверительного интервала

дата

Рис. 4. Суммарный расход по периодам планирования на 2017 г. с учетом доверительного интервала

На основе полученного рас пределения напора гидроустановки h i , i = 1, N и расхода воды через турбины ГЭС q t , i = 1, N по периодам планирования был также выполнен расчет мощности и выработки электроэнергии ГЭС. В табл. 1. приведены суммарные значения плановых водно-энергетических характеристик на 12 декад (апрель-июль), полученные в результате модельных расчетов.

Специалист может рассчитать разные варианты водно-энергетического режима на основе построенной модели, путем варьирования весов c₁ и c₂ критериев оптимальности в целевой функции (5), руководствуясь целями планирования и учитывая специфику конкретной ситуации.

ЗАКЛЮЧЕНИЕ

По результатам проведенного исследования можно сделать вывод о перспективности использования разработанной модели для расчета водно-энергетических режимов НГЭС. В дальнейшем планируется усовершенствовать модель, заменить линейные зависимости объема водохранилище от уровня верхнего бьефа и уровня нижнего бьефа от суммарного расхода на нелинейные для более точного расчета. Значения характеристик и переменных, рассчитанные по линейной модели, могут использоваться в качестве начального приближения при построении нелинейной модели.

Таблица 1. Значения плановых водно-энергетических характеристик НГЭС (период с 01.04 по 31.07.2017 г.)

Характеристики режима	Миним. значения	Средние значения	Максим. значения
Суммарный объем притока, км3	35,6	40,9	46,2
Суммарный расход через турбины ГЭС, км3	29,66	31,39	32,70
Суммарные холостые сбросы, км3	1,54	5,13	9,10
Выработка электроэнергии, млн.кВт.ч	1080,3	1103,5	1110,3

Кроме того, необходимо выполнить сравнительный анализ разных подходов (имитационный, оптимизационный) и методов к планированию водно-энергетических режимов НГЭС и разработать единую методику расчета. На основе разработанных моделей и методики в дальнейшем планируется разработать программный комплекс, предназначенный для поддержки принятия решения специалистом о выборе водно-энергетического режима НГЭС.