Многокритериальное оценивание качества измерителей угловых скоростей космических аппаратов на основе лучевых диаграмм

Одной из проблем построения современных систем управления КА на этапе эскизного проекта является обоснование его технического облика. Ключевым элементом любой системы управления КА является информационно-измерительная система, включающая комплекс приборов, измеряющих параметры движения КА. Для решения задач определения ориентации КА в инерциальном пространстве широкое распространение приобрели измерители угловых скоростей (ИУС) различного принципа действия.

Широкий спектр технических характеристик ИУС, по которым оценивают пригодность к решению целевых задач КА, не всегда позволяет выработать единый критерий к выбору того или иного типа прибора.

Это вызвано рядом требований, среди которых выделяют:

– требования к метрологическим характеристикам;

– требования к эксплуатационным характеристикам;

– требования к унификации информационных протоколов и стыковочных узлов;

– требования к дополнительным функциям;

– требования к особенностям построения типов ИУС.

Сложность выбора обусловлена отсутствием единого стандарта к перечню технических характеристик ИУС, методик их расчета и условиям их получения.

Несмотря на многообразие характеристик ИУС, основными из них, на наш взгляд, являются следующие:

• -    диапазон измерения в град/с;

• -    систематический дрейф нулевого сигнала в град/ч;

• -    случайный дрейф нулевого сигнала в град/ч;

• -    нелинейность масштабного коэффициента в %;

• -    устойчивость к перегрузкам;

• -    магнитная чувствительность (град/ч/Эрстед);

• -    температурная чувствительность (град/ч/°С);

• -    частота опроса;

• -    энергопотребление;

• -    габариты;

• -    масса.

Для решения этой задачи выбора измерительных средств, как правило, прибегают к формированию общего показателя качества измерительного прибора, составляющими которого могут являться метрологические и эксплуатационные характеристики, приведенные выше.

При выборе комплексного показателя качества измерительных средств придерживаются следующих правил. Комплексные показатели должны быть представительными, то есть характеризовать удовлетворение представленными требованиями, критичными (чувствительными) к изменениям исследуемых характеристик, обобщенными, то есть достаточно полно учитывающими все основные свойства и условия эксплуатации измерительного устройства, простыми в смысле наглядности и учитывающими факторы неопределенности.

Неоднородность технических характеристик и противоречивость их достижения приводят к необходимости решения многокритериальной задачи при выборе наилучшего измерительного средства. В работе предлагается применение технологии лучевых диаграмм при обосновании выбора измерителей угловых скоростей для системы управления КА.

Сущность технологии лучевых диаграмм

К сожалению, во многих практических случаях задача многокритериального выбора сводится к оценке отдельных показателей качества - без должного методического обоснования и обеспечения системной целостности. В лучшем случае заказчику (лицу, принимающему решение) предоставляются таблицы показателей качества для сравниваемых вариантов, трудно воспринимаемые и не дающие явного указания для предпочтения. Для агрегации частных оценок применяются алгоритмы аддитивной, мультипликативной или гармонической сверток, максимизация минимальной и максимальной эффективности и другие [1; 2]. Выбор метода агрегации трудно поддается аргументации и плохо воспринимается с точки зрения наглядности. Поэтому важнейшую роль играют проблемы визуализации количественных оценок системных свойств и, в особенности, агрегации этих оценок - для принятия окончательного решения о выборе одного из сопоставляемых вариантов.

Одним из инструментов принятия решений в такой парадигме является построение лучевых, или радиальных, диаграмм. Лучевая диаграмма представляет собой совокупность (по числу свойств сравниваемых объектов) лучей, на каждом из которых откладываются метки одного из нормализованных показателей. Метки разных объектов соединяются линиями различного цвета (структуры). Образованные ими многоугольники позволяют с предельной наглядностью выполнить многоаспектное сопоставление объектов самого различного назначения (рис. 1).

ВЕСТНИК РОСНОУ. Серия «Сложные системы …»

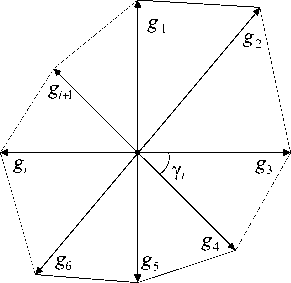
Рис. 1. Лучеграмма частных показателей

В частности, в работе [3] выполнено многокритериальное оценивание различных вариантов построения (конфигурирования) гидроакустического комплекса «Вектор» по 12 параметрам на основе технологии лучевых диаграмм, а в [4] решается задача экспертной оценки и выбора антивирусных средств на основе взвешенной оценки восьми частных показателей.

В общем случае среди сравниваемых вариантов нет превосходящих прочие по всем показателям. Тогда подсознательно выбирается вариант, ограничивающий большую площадь.

Площадь каждой фигуры вычисляется как сумма площадей составляющих ее треугольников:                        1 _M

^S = E g i g i + i^sin Y i .                                  ⁽¹⁾

• ² i = 1

Здесь M – число показателей, { g_i } – «радиальные» стороны треугольников, т.е. частные показатели соответствующего варианта ( g_{M + 1} ^ g ₁) , а { у i } - центральные углы. При симметричном расположении лучей все углы равны, что позволяет сравнивать варианты по значениям легко вычисляемой формулы

S * = E i g i g i + 1 .                                      ⁽²⁾

Рассмотрим технологии работы с лучевой диаграммой , основанные на применении формулы (1).

Здесь важно отметить специфику учета «отрицательных свойств», полезность которых убывает с ростом показателя. Отрицательными обычно назначаются затратные компоненты (негативный признак) – стоимость, эксплуатационные расходы, вес, энергопотребление, время реакции, погрешности, уход гироскопа, задержки выполнения работ и т.п. Такой подход заведомо исключает «площадную» интерпретацию и тем самым подрывает идейную основу предлагаемой технологии. Для «отрицательных» свойств можно изменить принцип нормировки : по каждому из них минимальное значение делится на достигаемое в соответствующем варианте. Существуют и другие варианты нормировки, изложенные в работе [5].

Дополнительную возможность учета важности показателей можно реализовать введением корректирующего множителя (индекса значимости показателя качества).

Далее, значения сумм (1) и (2) зависят от порядка перечисления показателей (точнее, от подбора пар). Это дает возможность применительно к каждой задаче дополнительно учесть полезность парных комбинаций показателей.

Эффект учета парных комбинаций можно усилить изменением центральных углов – распределением их суммы 2π пропорционально полезности пар. Разуме- ется, в таком случае решение должно приниматься на основе полной версии формулы (1).

Построение диаграмм и вычисление упомянутых площадей достаточно легко поддаются автоматизации. Это реализовано в разработанном одним из авторов программном средстве «Лучеграмма» [3]. Нужно помнить, что данное программное средство всего лишь инструмент и необходимо уметь им правильно пользоваться. Выполним решение задачи многокритериального выбора измерителей угловых скоростей систем управления космических аппаратов с использованием данного программного средства.

Учет весов частных показателей и углов между ними

Выбор пар частных показателей и значения угла между их лучами играет важную роль в получении результирующей оценки комплексного показателя качества. В этом случае можно руководствоваться следующим правилом. Частные показатели разбиваются на пары в соответствии с их значимостью. Так, например, одновременное достижение высоких показателей точности и низких массогабаритных характеристик является, вообще говоря, противоречием. В этом случае, если проектировщик решает задачу выбора малогабаритных измерителей с наилучшими показателями точности, то целесообразно объединить в пару показатель массы прибора среднеквадратическую погрешность его измерений. При этом угол между лучами выбирается максимальным, в силу приоритета этих показателей качества. Таким же образом необходимо поступать в случаях выставления других приоритетных пар частных показателей.

В некоторых случаях для придания дополнительного приоритета одного показателя над другими повышают его вес. Геометрический смысл повышения веса частного показателя заключается в увеличении длины его вектора (рис. 1).

Одинаковый угол между лучами частных показателей может быть в двух случаях, либо между ними отсутствуют явные приоритеты, либо они независимы друг относительно друга. На практике это встречается редко. Как правило, любое измерительное средство выбирается исходя из определенных предпочтений, а улучшение одного показателя влечет за собой ухудшение другого (паретооптимальные системы).

Расчеты комплексных показателей качества измерителей угловых скоростей

В качестве примера проведем отбор гироскопических измерителей вектора угловой скорости (ГИВУС) производства НИИ ПМ имени академика В.И. Кузнецова. Данные типы ИУС использовались и используются на различных типах КА и орбитальных станций. В рассмотрение примем ГИВУС на базе поплавковых гироскопов КИНД34-020, динамически настраиваемых гироскопов КИНД34-038, волоконно-оптических гироскопов КИНД34-064, а также микромеханических гироскопов КИНД34-070, являющихся в настоящее время опытными образцами.

Распределим частные показатели измерителей угловой скорости в соответствии с приоритетом. Как уже отмечалось, среди них важнейшими являются метрологические характеристики.

• 1)    среднее значение смещения нуля, град/ч;

• 2)    среднеквадратичное отклонение смещения нуля, град/ч;

• 3)    диапазон измеряемых угловых скоростей, град/с;

• 4)    погрешность масштабного коэффициента, %;

• 5)    количество осей;

• 6)    ресурс, лет;

• 7)    энергопотребление, не более, Вт;

• 8)    масса, кг.

К числу метрологических характеристик относятся:

• –    систематические и случайные составляющие дрейфа погрешностей;

• –    погрешность масштабного коэффициента;

• –    диапазон измеряемых угловых скоростей.

ВЕСТНИК РОСНОУ. Серия «Сложные системы …»

К числу эксплуатационных характеристик относятся:

• –    количество осей;

• –    энергопотребление;

  – масса;

  – ресурс.

Выбор оптимального варианта из множества возможных целесообразно проводить в виде последовательности шагов, на каждом из которых необходимо вносить изменения в исходные данные для учета предпочтений.

• 1    шаг . Выполним расчет комплексного показателя для исходного набора данных о технических характеристиках измерителей угловых скоростей. В наборе содержатся значения частных показателей качества четырех измерителей угловых скоростей: КИНД34-020, КИНД34-038, КИНД34-064, КИНД34-070. В исходном варианте примем углы между осями лучеграммы равными, а веса частных показателей установим в единицу (табл. 1).

Таблица 1

Значения показателей сравниваемых вариантов на первом шаге

№ п/п	Обозначение	Признак	Угол	Вес	КИНД34-020	КИНД34-038	КИНД34-064	КИНД34-070
1.	w_0	–	45	1	3	5	1	100
2.	sigma_0	–	45	1	0,005	0,003	0,001	30
3.	D	+	45	1	0,4	2	1,8	40
4.	dK	–	45	1	0,005	0,001	0,001	2
5.	Axis	+	45	1	4	6	4	3
6.	Y	+	45	1	10	5	15	0,5
7.	P	–	45	1	92	35	70	1
8.	m	–	45	1	12,6	4,7	10	0,6

Выполним нормировку значений частных показателей и последующий расчет комплексного показателя для каждого варианта (табл. 2), а также построим лучеграм-му (рис. 2).

Таблица 2

Значения нормированных показателей и результаты вычислений на первом шаге

№ п/п	Показатель	КИНД34-020	КИНД34-038	КИНД34-064	КИНД34-070
1.	w_0	0,3333	0,2	1	0,01
2.	sigma_0	0,2	0,3333	1	0,00003
3.	D	0,01	0,05	0,045	1
4.	dK	0,2	1	1	0,0005
5.	Axis	0,6667	1	0,6667	0,5
6.	Y	0,6667	0,3333	1,0000	0,0333
7.	P	0,0109	0,0286	0,0143	1
8.	m	0,0476	0,1277	0,06	1
Ранг и оценка варианта (площадь фигуры)		4 (0,2376)	2 (0,5322)	1 (0,8833)	3 (0,3750)

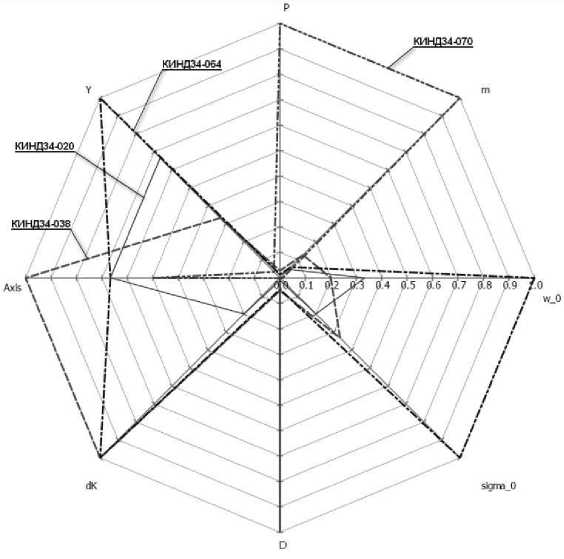
Рис. 2. Лучеграмма частных показателей ДУС серии КИНД

• 2    шаг . Гироскоп КИНД34-070 целесообразно исключить из дальнейших расчетов по причине того, что он существенно уступает по точности другим типам гироскопов и не может быть применим в высокоточной системе определения ориентации КА.

Как видно из лучеграммы (рис. 2), площадь фигуры, образованной частными показателями гироскопа КИНД34-020, существенно меньше остальных вариантов. Вследствие этого данный датчик можно также исключить из рассмотрения. Выполним новый расчет для оставшихся вариантов исходных данных (табл. 3; 4; рис. 3).

Таблица 3

Значения показателей сравниваемых вариантов на втором шаге

№ п/п	Обозначение	Признак	Угол	Вес	КИНД34-038	КИНД34-064
1.	w_0	–	45	1	5	1
2.	sigma_0	–	45	1	0,003	0,001
3.	D	+	45	1	2	1,8
4.	dK	–	45	1	0,001	0,001
5.	Axis	+	45	1	6	4
6.	Y	+	45	1	5	15
7.	P	–	45	1	35	70
8.	m	–	45	1	4,7	10

ВЕСТНИК РОСНОУ. Серия «Сложные системы …»

Таблица 4

№ п/п	Показатель	КИНД34-038	КИНД34-064
1.	w_0	0,2	1
2.	sigma_0	0,3333	1
3.	D	1	0,9
4.	dK	1	1
5.	Axis	1	0,6667
6.	Y	0,3333	1
7.	P	1	0,5
8.	m	1	0,47
Ранг и оценка варианта (площадь фигуры)		2 (1,5085)	1 (1,8874)

• 3    шаг . Выполним расстановку весовых коэффициентов частных показателей в зависимости от их важности в конкретной области применения. Выполним расчет с учетом весов (табл. 5; 6).

Таблица 5

Значения показателей сравниваемых вариантов на третьем шаге

№ п/п	Обозначение	Признак	Угол	Вес	КИНД34-038	КИНД34-064
1.	w_0	–	45	1,5	5	1
2.	sigma_0	–	45	1,4	0,003	0,001
3.	D	+	45	1	2	1,8
4.	dK	–	45	1,2	0,001	0,001
5.	Axis	+	45	0,5	6	4
6.	Y	+	45	1	5	15
7.	P	–	45	1,2	35	70
8.	m	–	45	1,4	4,7	10

Таблица 6

Значения нормированных показателей и результаты вычислений на третьем шаге

№ п/п	Показатель	КИНД34-038	КИНД34-064
1.	w_0	0,2	1
2.	sigma_0	0,3333	1
3.	D	1	0,9
4.	dK	1	1
5.	Axis	1	0,6667
6.	Y	0,3333	1
7.	P	1	0,5
8.	m	1	0,47
Ранг и оценка варианта (площадь фигуры)		2 (1,6782)	1 (2,2038)

Заметим, что изменение весов частных показателей не влияет на их нормированные значения (то есть диаграмма будет иметь вид, как на рис. 3), но вносит вклад в значения площадей фигур лучеграммы.

• 4    шаг . Для учета взаимной связи свойств сравниваемых вариантов расставим частные показатели попарно. Для этого предварительно построим граф, вершинами которого будут являться номера частных показателей, а дугами отметим наличие зависимости между показателями (рис. 4). Причем, сплошными линиями соединим вершины при положительном влиянии показателей, и штриховыми – при отрицательном влиянии показателей друг на друга.

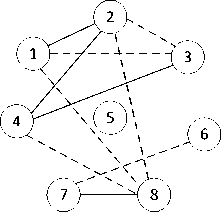
Рис. 4. Взаимная связь свойств сравниваемых вариантов

ВЕСТНИК РОСНОУ. Серия «Сложные системы …»

Расставим частные показатели с учетом их взаимного влияния и выполним расчет (табл. 7; 8; рис. 5).

Таблица 7

Значения показателей сравниваемых вариантов на четвертом шаге

№ п/п	Обозначение	Признак	Угол	Вес	КИНД34-038	КИНД34-064
1.	w_0	–	45	1,5	5	1
2.	sigma_0	–	45	1,4	0,003	0,001
3.	dK	–	45	1,2	0,001	0,001
4.	D	+	45	1	2	1,8
5.	Axis	+	45	0,5	6	4
6.	P	–	45	1,2	35	70
7.	m	–	45	1,4	4,7	10
8.	Y	+	45	1	5	15

Таблица 8

Значения нормированных показателей и результаты вычислений на четвертом шаге

№ п/п	Показатель	КИНД34-038	КИНД34-064
1.	w_0	0,2	1
2.	sigma_0	0,3333	1
3.	dK	1	1
4.	D	1	0,9
5.	Axis	1	0,6667
6.	P	1	0,5
7.	m	1	0,47
8.	Y	0,3333	1
Ранг и оценка варианта (площадь фигуры)		2 (1,7677)	1 (2,3641)

• 5    шаг . Для учета важности парных комбинаций показателей может быть изменен угол между ними. Например, у наиболее важных комбинаций пар угол увеличивается, а у наименее важных – уменьшается, что в итоге оказывает влияние на площадь фигуры (табл. 9; 10; рис. 6). В нашем варианте увеличим углы между 3-м и 4-м, 4-м и 5-м, 6-м и 7-м показателями в силу их отношений к метрологическим и эксплуатационным характеристикам соответственно.

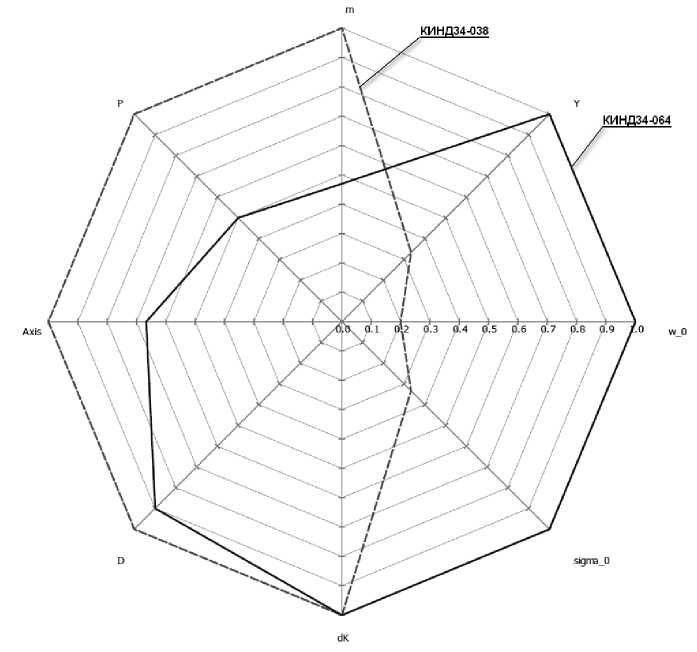
Рис. 5. Учет зависимости взаимного влияния показателей друг на друга

Таблица 9

Значения показателей сравниваемых вариантов на пятом шаге

№ п/п	Обозначение	Признак	Угол	Вес	КИНД34-038	КИНД34-064
1.	w_0	–	10	1,5	5	1
2.	sigma_0	–	10	1,4	0,003	0,001
3.	dK	–	90	1,2	0,001	0,001
4.	D	+	70	1	2	1,8
5.	Axis	+	10	0,5	6	4
6.	P	–	80	1,2	35	70
7.	m	–	45	1,4	4,7	10
8.	Y	+	45	1	5	15

ВЕСТНИК РОСНОУ. Серия «Сложные системы …»

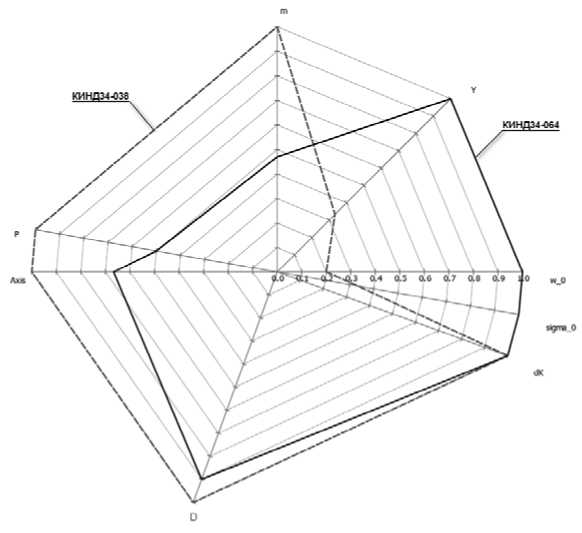
Рис. 6. Учет важности парных комбинаций показателей

Таблица 10

Значения нормированных показателей и результаты вычислений на пятом шаге

№ п/п	Показатель	КИНД34-038	КИНД34-064
1.	w_0	0,2	1
2.	sigma_0	0,3333	1
3.	dK	1	1
4.	D	1	0,9
5.	Axis	1	0,6667
6.	P	1	0,5
7.	m	1	0,47
8.	Y	0,3333	1
Ранг и оценка варианта (площадь фигуры)		1 (1,9419)	2 (1,8131)

Заключение

На основе полученных результатов расчетов можно сказать, что учет различных предпочтений в зависимости от контекста решаемой задачи значительно влияет на значение комплексного показателя оцениваемых вариантов. Данное влияние может быть отражено в виде изменения степени предпочтительности выбора одного варианта перед другим вплоть до полной смены оптимального варианта (табл. 11).

Несмотря на различные предпочтения, видно, что лидером среди ГИВУС является КИНД34-064. Это не удивительно, поскольку он является самым совершенным в настоящее время и превосходит своих предшественников (КИНД34-020 и КИНД34-038) по точности, стабильности масштабного коэффициента, а также по ресурсу.

Таблица 11

Результаты расчетов для шагов модификации исходных данных

№ п/п	Описание варианта исходных данных для расчета	Вариант 1 (КИНД34-038)	Вариант 2 (КИНД34-064)
1.	Исходный вариант (равные углы, веса показателей равны 1, произвольный порядок следования показателей)	1,5085	1,8874
2.	Учет весов частных показателей (добавление коэффициента)	1,6782	2,2038
3.	Учет взаимосвязи показателей (изменение порядка следования)	1,7677	2,3641
4.	Учет важности комбинаций пар (изменение углов между осями лучеграммы)	1,9419	1,8131

Интересным является применение технологии лучевых диаграмм при анализе метрологических характеристик средств измерения в процессе их функционирования в течение длительного этапа летной эксплуатации. Это позволит, во-первых, оценить степень их деградации в условиях возмущающих факторов космического пространства, а во-вторых, сформировать правила их оптимальной реконфигурации при возникновении метрологических отказов. Такой подход создает условия для реализации концепции адаптивных навигационных комплексов КА [6].