Многошаговый процесс обучения как движение в направлении увеличения компетентности студента по траектории, заданной учебными модулями

Множество учебных модулей дисциплин технического вуза с топологической точки зрения представляет собой сеть, движение по узлам которой задает множество возможных траекторий для отдельного студента или групп студентов от начального состояния (абитуриент) до конечного (дипломник). В рамках этого представления учебный процесс является графом, ориентированным на прохождение студентом учебных модулей и определенным для разновидностей сети, узлы которой 1...iJ...N, образующие непустое конечное множество, соответствуют этим учебным модулям общим числом N. Подмножество У множества NkN, составленного из элементов (i,у), представлено дугами, связывающими различные модули и указывающими на возможность перехода от узла i к узлу j. Если пометить в этой сети каждый модуль целым числом, присвоив ему соответствующий номер таким образом, что будет справедливо неравенство i < j, и ввести веса дуг, связывающих соответствующие узлы, то общая схема образовательного процесса в определенном смысле может быть сведена к процедуре многошагового процесса принятия решений. Полагая в рамках структурно-компетентностного подхода к обучению [1], что образовательный процесс в техническом вузе должен быть ориентирован прежде всего на обеспечение максимального уровня компетентности выпускников, будем считать, что в роли весов дуг должны выступать определенные некоторым образом частные коэффициенты компетентности [2]. Тогда проблема повышения компетентности в общем виде будет сводиться к отысканию траектории, при движении по которой от начального общеобразовательного модуля до конечного модуля дипломного проектирования происходило бы постепенное наращивание уровня компетентности f до его максимально возможного значения /шах аддитивным образом. Приращение t. к значе- ниюД при переходе от модуля i к модулю j будет равняться длине дуги (iД) перехода от одного узла сети к другому. Для конкретности представим себе, что мы имеем дело с гипотетическим учебным процессом, насчитывающим всего девять учебных модулей (рис. 1).

На рис. 1 направление учебного процесса по пути (Т() ►('У) ^^ будет включать несколько частных подпутей, например^ —-► : -►■. и1 ; -* : . Направление учебного процесса по траектории

(^y^^^XjD^KZD^K^ (рис. 2) представляет наихудшую стратегию, поскольку эта стратегия обеспечивает наименьший уровень компетентности на выходе из стен учебного заведения, а по траектории

Помимо стратегий, изображенных на рис. 2 и 3, для гипотетического учебного процесса (см. рис. 1) можно выделить еще 63 возможные стратегии. В то же время существует единственная стратегия учебного процесса, являющаяся оптимальной для всех учебных модулей. Оптимизационная задача, сформулированная в этом варианте, включает целые классы подзадач, сами по себе также являющиеся оптимизационными, каждую из которых можно свести к задаче линейного программирования - максимизировать значение

^[ p , ⁽ x , ) + p ₂( x ₂) + ... + p_n ( x „ ) + ... + P n ( x N )]      ⁽¹⁾

при имеющихся ограничениях на ресурсы:

c i ⁽ x i ) ⁺ c 2 ⁽ x 2 ) ⁺ ... ⁺ c n ⁽ x n ) ⁺ ... ⁺ c N ⁽ x N ) ^ K ,

0<х_п<В,п = 1,2, ..., N , х _п - целые числа, (2) где К и В - константы; функции с_п ( х_п ) неотрицательны и принимают целые значения, с ( х ) = 0; p_n ( x_n ) - известные, но произвольные функции, обладающие свойством

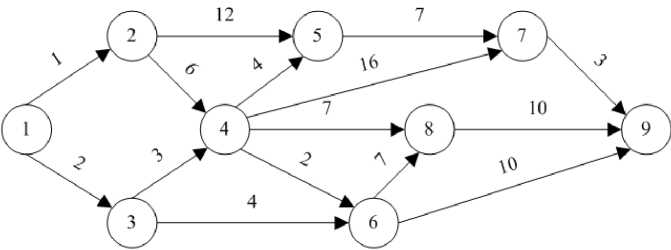
Рис. 1. Схема гипотетического учебного процесса, состоящего из девяти модулей. Числа вдоль дуг соответствуют условным вкладам t ..

в уровень компетентности при движении от модуля к модулю

Рп ( ^хп ) = 0- В сформулированной таким образом задаче функции с , ( х , ) ир _п ( х , ) заданы, а переменными являются ^х ₁, ^х ₂,..„ X n ,^,x _N .

Если интерпретировать эту задачу в терминах проблемы повышения уровня компетентности выпускников, то функции р , ( х , ) должны представлять собой не что иное, как аддитивные вклады в компетентность студентов, теоретически достижимую после прохождения ими дисциплин соответствующих учебных модулей, а функции с , ( х _п ) - имеющийся учебный ресурс (например, часы учебной нагрузки), необходимый для организации учебного процесса- В такой интерпретации задача линейного программирования заключается в максимизации уровня компетентности при условии, что общее количество учебных часов не выйдет за рамки предусмотренного стандартом объема аудиторных занятий в учебном плане- Решение оптимизационной задачи в этом варианте можно свести к рассмотрению многошагового процесса принятия решений, имея в виду, что обучение производится по курсам и семестрам-

Рассмотрим ситуацию, когда к определенному моменту времени обучение студенческой группы, начиная от первого и кончая ( п - 1)-м учебного модулем, уже закончилось- Пусть на этом этапе мы имеем недоиспользованный учебный ресурс некоторого объема, равный ве-личине у - Эти оставшиеся недоиспользованными у единиц ресурса необходимо оптимально распределить с целью доведения учебного процесса до конца-

Пусть/(п, у) - максимально возможный уровень компетентности, который можно обеспечить путем распре-деленияу единиц учебного ресурса- Величина/(1, К) является в данном случае решением исходной оптимизационной задачи, которая была погружена в семейство, состоящее из N (К + 1) задач- Теперь требуется определить значения/(п, у)дляп = 1,2, ., Nиу = 0, 1, 2, .,К-Имеющаяся ситуация характеризуется с помощью пары значений (п, у), в которой содержится вся информация, необходимая для принятия текущего решения в рассматриваемом узле сети, причем можно не учитывать того, каким образом произошел переход в состояние (п, у)-Значениер,(х,) +/[п + 1,у - с,(х,)] представляет максимальный уровень компетентности, которого можно достичь путем перераспределенияу единиц ресурса для организации учебного процесса- Максимизируя это выражение по х,, будем искать величину

/( ^{п ,} у ⁾=тах , М? , ^{( х} п ^{) +}

+Л п + 1, у - с _п ( х _п )]| х - допустимо}- (3) Выражение (3) справедливо для п 8 <  N, если положить

/ ( N +1 _<у ) = 0, у = 0,1,2,., К. (4)

Это означает, что недоиспользованный ресурс оказывается бесполезным, и такое предположение применительно к учебному процессу вполне реалистично, поскольку при организации процесса обучения нельзя ввести понятие издержек учебного производства за переход недоиспользованного учебного ресурса в следующий период-

Соотношение (3) представляет собой систему функциональных уравнений, однако при решении задачи организации учебного процесса следует иметь в виду, что мы имеем дело не с четко сформулированной управленческой задачей, а с образовательным процессом, плохо поддающимся формализации- Сложность рассмотрения в данном случае заключается в том, что переходы осуществляются не просто от одного узла сети к другому, а от некоторого плохо формализуемого состояния к другому состоянию, причем отдельное состояние представляет

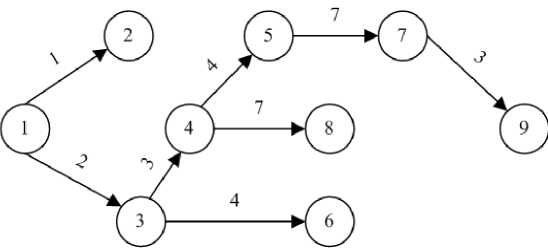
Рис. 2. Пример частной стратегии многошагового управления гипотетическим учебным процессом, обеспечивающей наименьший конечный уровень компетентности для сети, показанной на рис. 1

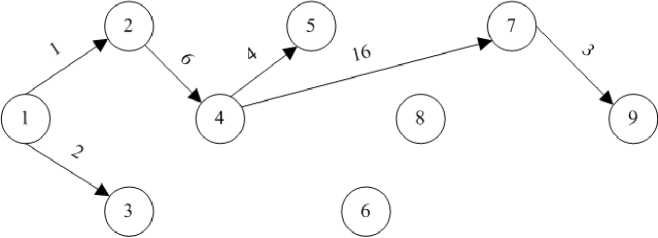
Рис. 3. Пример частной стратегии многошагового управления гипотетическим учебным процессом, обеспечивающей наибольший конечный уровень компетентности для сети (см. рис. 1)

собой точку учебного процесса, в которой принимается решение. Описание каждого такого состояния желательно провести с такой степенью детализации, которая позволила бы дать оценку альтернативным решениям, относящимся к организации учебного процесса.

При переходе на язык состояний погружение во множество оптимизационных задач эквивалентно введению понятия пространства состояний, представляющего собой множество возможных состояний системы:

S „ ={( и , у )| у = 0,1,2,., ^ }.        (5)

Оптимальной стратегией в этом случае будет такая стратегия, которая станет оптимальной одновременно для каждого состояния, и будет обладать свойством, что какими бы ни были начальные состояния и решения, последующие решения станут формировать оптимальную стратегию для состояния, возникающего после первого перехода.

Еще одна сложность рассмотрения задачи оптимизации учебного процесса заключается в том, что мы имеем дело с переходами из одного неоднозначно определенного состояния системы в другое, и поэтому в данном случае чисто такой подход к разрешению проблемы оказывается несостоятельным. Можно сказать, что детерминистский подход к решению проблемы невозможен постольку, поскольку процесс обучения всегда содержит значительный элемент неопределенности. Поэтому при описании процесса наращивания компетентности при движении от состояния к состоянию мы вынуждены отойти от детерминистского подхода в пользу стохастического, передя на язык вероятностей и статистики. Введем в рассмотрение величину / ( и , i ), представляющую собой максимальное значение математического ожидания уровня компетентности, который можно достигнуть в периодах и , и + 1,., N , если процесс обучения находится в состоянии ( и , i ). Горизонт планирования учебного процесса в данном случае будет состоять из N периодов (семестров), каждый из которых нумеруется целыми числами от 1 до N , причем величина N связана со ступенью образования и варьируется в зависимости от того, с кем мы имеем дело - бакалаврами, магистрами или стажерами. Переход от модуля к модулю эквивалентен переходу от периода и к периоду и + 1.

Введем далее следующие обозначения: R k ( n ) -уровень компетентности, достигаемый при выборе к -го решения в ( и , i )-м состоянии; P j ( n ) - вероятность перехода из состояния ( и , i ) в состояние ( и + 1,у) при выборе к -го решения. Величина

R k ( n ) ⁺ £ j P ( n ) f ( n + 1, j)           (6)

представляет собой математическое ожидание уровня компетентности при начальном состоянии ( и , i ), выборе решения к и следовании оптимальной стратегии для дальнейшего движения от и + 1 до N . Эта величина не может превышать значения/( и , i ). Путем максимизации выражения (6) по к можно получить следующее соотношение: f ( n , i ) = max[ R k ( n ) + £ _jP j ( n ) f ( n + 1, j )] .   (7)

Оно справедливо при и <  N , а также при и = N , если положить/( и + 1, j ) = 0.

Если уровень компетентности задан (например, рынком), то исходя из этого уровня следует решать функциональное уравнение в направлении убывания и, т. е. ис пользовать метод обратной прогонки. В данной постановке задачи метод прямой прогонки оказывается непри годным, поскольку используемая модель является моделью марковского типа, которая описывает стохастический процесс, содержащий большой элемент неопределенности. В этой модели с конечным множеством состояний от 1 до т требуется максимизировать математическое ожидание уровня компетентности, полученное за весь процесс обучения студента. Для каждого такого состояния имеется конечный набор решений, однозначно соотносящийся с теми учебными методами и технологиями, которые применяются в данном состоянии. Можно ввести локальную функцию компетентности, равную m h (i, k, v) = Rk( n) + £ jj,            (8)

j = 1

где v(j ) сокращено до v в силу того, что v(j ) является элементом вектора v размером тх1. Решения принимаются в периоды 0, 1,2,... и т. д., представляющиеся одинаковыми промежутками времени, равными по продолжительности отдельным семестрам, величина с - это показатель дисконтирования за период, 0 <  с < 1.

Допустим, в период и наблюдается состояние i и выбрано решение к. По локальной функции компетентности следует, что вероятность перехода из состояния i в состо-яниеу в период (и + 1) равна Pij. Логично сделать предположение о том, что m

£ P j <  1 .                   (9)

j = 1

Это неравенство предполагает, что стохастический процесс обучения может быть искусственно приостановлен на некотором шаге (например, студент может быть отчислен из-за крайне низкого уровня компетентности). В случае прерывания процесса переход в некоторое другое состояние в следующем периоде (семестре) не осуществляется.

Процесс обучения начинается в момент зачисления абитуриента и может продолжаться неопределенно долго при учете послевузовских форм обучения и повышения квалификации. При таком подходе стратегия Г определяет решение 8( i ) для состояния i . Уровень компетентности, достигаемый стратегией 8, можно представить с помощью т -мерного вектора R ⁸, а вероятность переходов - записать в виде матрицы переходных вероятностей Р ⁸ размера т х т :

( R ⁸ ) i = R ^S(i\                      (10)

( P ⁸ ) у = P j ⁸ i ⁾.                    (11)

Модель с дисконтированием (переходный режим) можно определить как модель, в которой выполняются следующие гипотезы:

• -    гипотеза 1:

c £ P k <  1 при всех i,к ;            (12)

j = 1

• -    гипотеза 2: для всякой стратегии обучения собственные значения

I cP <  1 .                      (13)

N

Гипотеза 1 справедлива, если соотношение £ Pj < 1 j=1 выполняется как строгое неравенство, или если с < 1. Это означает, что процесс может остановиться на некотором шаге, т. е. переход в следующее состояние не осуществляется. Стратегия 2 определяет режим переходного периода.

Для того чтобы ( cP ⁸) ^ 0 при п ^ <», достаточно выполнения любой из двух приведенных выше гипотез. При этом неймановская последовательность 1 + ( cP ⁸ ) + ( cP ⁸ )² + ... сходится к матрице, обратной к ( I- cP ). В этом случае I - единичная матрица размера т х т . Поскольку в рассматриваемой модели имеется т состояний, то функцию уровня компетентности для стратегии 8 можно записать в виде вектора длиной т , а уравнение стратегий переписать в матричном виде. Для того чтобы получить само уравнение стратегий, необходимо учитывать, что каждая стратегия обучения 8 связана с функцией компетентности v ⁸, где v ⁸( s ) определяет агрегированный уровень компетентности, которого можно достигнуть, исходя из состояния s и используя стратегию обучения 8. Выражение «использовать стратегию обучения» означает, что в состоянии s выбирается решение 8( s ), затем предполагается, что процесс перешел в состояние s ‘, в котором выбирается решение 8( s ‘‘) и т. д. Функция уровня компетентности зависит от последовательности состояний и решений о вознаграждениях, связанных с рейтинговой системой вуза, а также от способа агрегирования поощрений, т. е. от того, насколько удачно рейтинговая система вписывается в структуру управления учебным процессом.

Если ограничиться состоянием s и отдельным решением d , то можно рассматривать многошаговый процесс принятия решений как усеченный. В этом случае такой процесс ведет себя так же, как исходный неусеченный процесс, но только в течение одного перехода, а затем останавливается. Закон перехода и способ агрегирования вознаграждений отражаются в неявном виде посредством функции компетентности v. Отсюда должен произойти переход из состояния s в состояние s ‘, при котором теоретически может быть получено вознаграждение v ( s ‘) в виде соответствующих оценок или баллов, а затем процесс останавливается.

Состояния s , решение d и дисциплинарная функция компетентности v являются тремя переменными для модульной функции компетентности h ( s , d , v ), которая определяется как суммарный уровень компетентности, получаемый в усеченном одношаговом процессе, причем сам процесс начинается из состояния s , где принимается решение d , а дисциплинарная функция вознаграждения есть v . Функция v отображает множество s на действительную ось. Корректной функции v в действительности существовать не может, поскольку при изучении какой-то отдельной дисциплины, входящей в соответствующий модуль, нельзя учесть все составляющие компетентности и абсолютно точно вычислить уровень показателей, позволяющий выпускнику соответствовать требованиям рынка. Поэтому введение функции v позволяет лишь формально записать способ перехода процесса принятия решений при обучении студентов и сформулировать метод агрегирования вознаграждений, базирующийся на рейтинговой системе.

Модульная функция компетентности может быть разъяснена следующим образом. Если видоизменить модель распределения учебного ресурса, в которой со стояние s в соответствии с выражением (5) определяется парой (п, у), а решением является хп, то модульная функция компетентности принимает вид

• ^{h [( п ,} У ^{), х} „ ^{, v} ] = Р_п ^{( х} „ ^{) + v} [ ^п + 1^, У ^{- c} „ ^{( х} „ ^)]<  ^N . ⁽14⁾

В этом случае осуществляется переход в состояние [ п +1, у - c ( х )], и в данный момент будет получено дисциплинарное вознаграждение. Поскольку компетентность является аддитивной величиной, мы должны добавить это значение к р ( х ). Но выражение (14) несправедливо при п = N . Действительно, если требовать чтобы состояниям соответствовали связанные с ними решения, т. е. чтобы множество D ( s ) было не пусто, то исчезает возможность вводить состояние ( N+1, z ). Таким образом, переход осуществляется из состояния N , образно выражаясь, «в никуда», и при этом

^ ^[( и , y ), x_n ,v] = P n ⁽ x N ) .             ⁽¹⁵⁾

Если ограничиться таким подходом, то оказывается, что выпускник технического вуза, получив диплом, прерывает не только связь с «alma mater», но весь процесс образования, что ограничивает возможности повышения уровня компетентности в ходе дальнейшего послевузовского образования. Изменяя v , можно восстановить нормальный закон протекания процесса, величины вознаграждений и способ их агрегирования. При наличии нескольких стратегий возникает проблема их оценки. Для решения этой проблемы воспользуемся уравнением оценки стратегий:

v ⁸( s ) = h [ s , 8( s ), v ⁸],                 (16)

где все se 8.

В этом уравнении в левой части записан уровень компетентности, который обеспечивает использованием стратегии 8, а справа - компетентность при использовании дисциплинарной функции компетентности v8. Возникает вопрос о наличии возможных решений этого уравнения и единственности существования функции компетентности, удовлетворяющей уравнению (16). В случае положительного ответа v8определяется как единственная неподвижная точка оператора h [s, 8(s)]. Принцип оптимальности утверждает, что существует такая стратегия п, которая является оптимальной для всех состояний, откуда вытекает, что для такой стратегии функция компетентности vп будет наилучшей из всех возможных в том смысле, что при всех s из 5 и всех 8 из А vп( s )> v 8( s).                      (17)

С математической точки зрения неравенство (17) отражает факт существования такой учебной стратегии, функция компетентности для которой является верхней огибающей функцией компетентности для всех других возможных стратегий. Если рассматривается стратегия п, в которой первое решение п(s) изменено, а все остальные остаются прежними, то это изменение не оказывает влияния на компетентность, полученную после перехода и поэтому при всех s и всех d vп(s )>h ’[ s ,d, vп].                   (18)

В результате получим следующее соотношение:

v ^п( s ) = max _d { h ’[ s , d , v ^п]} привсех 5 .     (19)

Отметим, что принцип оптимальности эквивалентен утверждению о том, что оптимальная функция компе- тентности vп существует и является решением функционального уравнения.

Возвращаясь к модели с дисконтированием и переходному режиму, запишем уравнение стратегий в виде v8 - R8 + cP8v8.(20)

или

(Z-cP8 )-R8,(21)

где P8 и R8 взяты в соответствии с(10)и(11). Для матрицы (Z - cP8) существует обратная матрица, поэтому v8 = (I - cP8 )-1 R8.(22)

Отсюда следует, что уравнение стратегий имеет единственное решение, когда справедлива гипотеза 1 (12) либо (13). В этом случае можно рассмотреть задачу линейного программирования, полагая, что суммирование ведется по всему набору индексов, и вводя пределы суммирования

{ Y j Y k^X } ^ ^тах          (23)

при ограничениях

Y k X - c Y j Y kXPP = a , , i = 1,2,..., m , x j > 0 при всех i , k ,                  (24)

где a 1 , a ₂,..., a _m -любые положительные действительные числа. Известно, что данная задача допустима и ограничена, а ее оптимальный базис обладает следующими свойствами:

• 1)    для каждого i переменная x j положительна только для одного k ;

• 2)    п( i ) - k всякий раз, когда х , >  0 и стратегия является оптимальной.

Таким образом, стратегия п удовлетворяет формуле (22) и принципу оптимальности. Кроме того, v ^п представляет собой вектор двойственных переменных и удовлетворяет условиям дополняющей нежесткости для любого оптимального базиса прямой задачи. В то же время данная задача разрешается в рамках леонтьевской системы, одна из особенностей которой состоит в том, что один и тот же базис оптимален для всех положительных правых частей системы (24). Именно поэтому значения констант a . несущественны, если они положительны. Хотя приведенная модель с дисконтированием дает решения со многими состояниями при использовании метода аппроксимации, число возможных решений для каждого состояния не слишком велико.

Применительно к организации учебного процесса эта модель показывает, что при любой форме организации и любых учебных технологиях имеется единственная оптимальная стратегия, обеспечивающая для заданных условий наиболее высокий уровень компетентности выпускников, который определяется аддитивной функцией компетентности [1], базирующейся на дисциплинарной и модульной функциях. В случае если мы имеем дело с открытым образованием, целесообразнее использовать модель без дисконтирования. Для этой модели, не предусматривающей вероятности остановки образовательного процесса, выполняется следующая гипотеза:

c = 1, Y j P j = 1 для всех i , k .         (25)

В этой модели процесс принятия решений продолжается бесконечно. Вознаграждение в виде оценок получа ется в каждый период, в то время как будущий доход не дисконтируется. В этом случае суммарная компетентность, достигнутая за первые п периодов, теоретически должна стремиться к бесконечности при п^ ^ независимо от того, какая стратегия используется. В этом случае суммарное вознаграждение в виде оценок уже не является критерием, согласно которому можно выделять плохие и хорошие стратегии. Используя модели без дисконтирования, можно наиболее просто максимизировать средний уровень успеваемости за единицу времени. В этом случае приходится говорить о росте или снижении успеваемости, что само по себе может отражать изменение уровня компетентности лишь отчасти. Возвращаясь к задаче линейного программирования (23) при ограничениях

Y k X - Y j Y j XP = 0, i = 1,2,..., m ,   (26)

Y j Y j X k P j = 1; x^k k >  0 при всех i , k ,    (27)

мы видим, что приведенная модель допустима и ограничена. Ее оптимальный базис обладает следующими свой-k ствами: для каждого z переменная xj положительна не более чем для одного k, а определенные ниже переходные вероятности образуют одну эргодическую цепь {Pjj (xj > 0)}. Темп роста средней успеваемости для данной эргодической цепи является наибольшим среди всех возможных цепей. Иначе говоря, имеется возможность найти эргодическую цепь с максимальным темпом роста средней успеваемости. Эта цепь всегда будет давать наилучший темп прироста успеваемости для тех состояний, которые ее образуют. В большинстве случаев при организации учебного процесса такие состояния достижимы из других состояний, поэтому указанная эргодическая цепь дает наилучший темп роста для всех состояний. Однако в сложных случаях при возникновении нескольких таких цепей, например если обучение ведется по нескольким специальностям, эту задачу придется решать многократно с использованием процедуры типа декомпозиции. Максимальный темп роста средней успеваемости для модели без дисконтирования можно определить с помощью метода итеративных стратегий. В очень простых случаях метод итеративных стратегий равнозначен блочному преобразованию в двойственном симп-лекс-методе, как и в модели с дисконтированием.

Таким образом, мы убеждаемся, что организация учебного процесса в техническом вузе может представляться многошаговым процессом, базирующимся на вероятностных состояниях, включающих всю учебную предысторию. В ходе этого процесса вырабатываются самые различные стратегии, включая и наиболее оптимальную, которая может быть реализована посредством использования эффективных педагогических технологий, обеспечивающих выход на диктуемый рынком уровень компетентности. Поэтому на следующем этапе плодотворного использования модельной концепции в рамках структурно-компетентностного подхода встает задача рассмотрения, обсуждения, отбора и встраивания в учебный процесс таких педагогических технологий, которые могли бы наиболее продуктивно повышать компетентность выпускника в ходе учебного процесса.