Многоуровневая модель анализа прочности конструкций из полимерных композитов при многофакторном нагружении

Установлено [1], что закономерности ползучести основных конструкционных полимерных материалов в широком диапазоне напряжений удовлетворительно описываются линейными наследственными уравнениями. В общем случае пространственного теплового и напряженно-деформированного состояния краевая задача линейной наследственной теории ползучести сводится к решению уравнений наследственной термовязкоупругости.

Определение напряженно-деформированного состояния конструкций из полимерных композитов при многофакторном нагружении. На основании принципа соответствия решение задачи наследственной ползучести может быть приведено к решению соответствующей задачи упругости путем замены основных констант вязкоупругости материала соответствующими временными операторами с помощью прямого символического метода Вольтерра, либо применением преобразования Лапласа или Лапласа – Карсона к наследственным интегралам ползучести. Для этой же цели могут быть использованы методы преобразования Фурье или разложения в ряды других видов. Выбор метода зависит от физической модели рассматриваемых процессов и свойств материала конструкций.

Обозначим параметры пространственного теплового и напряженно-деформированного состояния (НДС), к которым применены указанные виды преобразований, верхним индексом « * », а временные операторы вязкоупругости, замещающие соответствующие константы вязкоупругости материалов, – верхней чертой. Представим воздействие внешних статических, динамических сил и тепловых источников в виде вектора полей температур T ± , тепловых потоков q ± , напряжений о ± и перемещений и ± на внутренней и наружной поверхностях оболочки корпуса несущей конструкции летательного аппарата: ±      ±   ±   ±    ±    ±   ±   ±   ±

О ^— { T , q , °_В, ^ 23 , ^ 33 , u 1 , u 2 , u 3 } .                                     ⁽¹⁾

Рассмотрим многослойную оболочку корпуса несущей конструкции летательного аппарата из вязкоупругих анизотропных материалов, отнесенную к криволинейной ортогональной системе координат x1,x2,x3 . Здесь, наряду с общей системой координат x1 ,x2,x3 , введена также и ло- кальная система x1k,x2k,x3 k, связанная с каждым слоем k . При этом каждая из поверхностей слоя k x3k = 0 совпадает с его срединной поверхностью радиусом Rckp . Для каждого слоя к многослойной оболочки справедлива система уравнений, которая получается на основе классической системы нелинейных уравнений теории упругости [2] в предположении геометрической ли- нейности деформаций еу относительно перемещений иу и физической нелинейности материала, обусловленной реологическими свойствами полимерных композитов. С учетом рассмотренных преобразований, исходную систему уравнений представим в тензорном виде:

до ij-

+ X, = 0 , ° у = Ee, ,

1 (^ t^ ] - M = 1. 2, 3 ,

2 дx,дx,

V j ¹ 7

где X _i – вектор объемных сил; Е – операторный модуль вязкоупругости; e_ij – деформация.

Для перехода от уравнений равновесия к уравнениям движения компоненты вектора объемных сил представим выражением:

• —         й ²u

X = X, — p , i = 1.2.3 .                          (3)

д t ₂

Применяя преобразование Лапласа к уравнению (3) и принимая параметр преобразования р = X , где X - эмпирическая константа материала, при начальных условиях и = и

t = 0 ,

д и _ д и д t д t

t = о

получаем:

TV *     -,,*                *    „

Xi = Xi — p X и — X и

V

д и t = о       д t

)

t = о

i = 1, 2, 3 .

Учитывая особенности геометрии формы конструкций оболочек с использованием коэф- фициентов Ламе H 1. H2, H3, исходную систему уравнений, справедливую для каждого слоя k многослойной оболочки, с учетом выражений (3)-(5), запишем в следующем виде:

– уравнения движения

д дx 1

( H 2 о *, )

—

д H ₂

д x ,

О

*

д _ . ,  дH,

+ — (H 1°12) +    О дx 2            дx 2

*

+ ^_ (H1H 2 0*3) + дx 3

, т т ^дH 1   * , тх *

+ H_? ---o_n + X, 2             13         1

д x 3

—

_ а 2 * p X и ,

—

X и ,

—

V

t = о

д t t = о 7

— ( H ,о*₂₂ ) — ^ H ¹ о *, +— ( H ₂о*₂ ) + ^{д H 2} о *₂ +— ( HH ₂о *₃ ) + 1   22                   1 1                  2   12                   12                  1    2   23

д x ₂              д x ₂        д x ,              д x 1         д x ₃

(

.     ^дH 2   *     Т^*       А 2 * А

+ H 1--- О 23 + X 2 — p X и 2 — X и 2

дx₃                                 t = о

д и ₂ д t

t = о

= о ,

— ( H ₂о *,) — H , ^ H 2 2    11             1

д x 1                   д x ₃

*

^О 22

. ^д / и — *

⁺ д ^{( H} 1 ^О 23

д x ₂

а

) + — ( H 1 H 2 о 33 ) д x ₃

—

дН 1 *      *

— H ₂ ^- 1 0.. + X₃ 2             11         3

д x ₃

—

p[x ² и 3

V

—

X и ₃

t = о

—

д и ₃ д t

\

t = о

= о ;

– физические уравнения связи напряжений и деформаций

*        1     *	V12 _*	V13 _*	_ *	1 _*
6 11 -"^-° 11 " E 11	o22 — E 22   22	J- O33 , E 33	6 12 "	73 O12 , G 12
*         1      *	V 12 _*	V 23 n^	_ *	1 _*
6 22 — 7;   O 22 E 22	— ^^O,, " E 22    11	73 O 33 , E 33	6 13	73 O13 , G 13
*         1      *	V13 _*	v 23 *d	_ *	1 * *
6 33 — 73 а 33 "  E 33	-^^o,, — E 33    11	7; O 2 2 , E 33	6 23	— _^_ O 23 . G 23

Здесь характеристики материала E и G представляют операторные модули вязкоупругости и вязкого сдвига соответственно, v - коэффициент Пуассона;

– геометрические уравнения Коши

*

6ц =

*

⁶ 22 ^—

*

⁶ 33 ^—

1 д u *

H ₁ д x ₁

1 д u *

H ₂ д x ₂

1 д u ₃ *

H 3

д x ₃

1   д H

+

H ₁ H ₂ д x ₂

+2

H ₂ H ₃ д x ₃

- +3

HH₃ д x

*      1    д H ₁

u 2 +

. * .

U 3 +

H 1 Н 3	u д x 3
1	д H
H 2 Н 1	u д x 1
1	д H 3

*

1 , u. +

¹    H ₂ Н ₃ д x ₂

*

' 3 ,

*

• 2 ,

– начальные условия

—*  —*

о —o

*

⁶ 12 ^—

*

⁶ 13 ^—

*

⁶ 23 ^—

1 д u *

H ₂ д x ₂

1 д u *

H ₃ д x ₃

1 д u 2

H ₃ д x ₃

до) *

t — о

,

д t

+

+

+

1 д u *

H ₁ д x ₁ , 1 д u ₃ *

H ₁ д x ₁ , 1 д u ₃ * ;

H ₂ д x ₂ '

до

-1 *

д t ) t — о

– граничные условия на наружной и внутренней поверхностях пакета слоев:

*   _ / + x*

° 13,1 = ^{( а} 13,1 ) ,

*   _ / +  x*

^O 23,1 = ^{( а} 23,1 ) ,

—*  —

= po — о

;

t — 0

* ^O 33,1

= ( 0 + 3,1 ) * ,

*       —п""

^а 13, k = ^{( а} 13, k ) , поверхностях контакта смежных слоев:

* u i , k

*      ^гт"

^а 23, k = ^{( а} 23, k ) ,

ГТ * — ^гт" V ■ ^а 33, k = ^{( а} 33, k ) ;

*

^— u , k + 1 ,

*

^O 33, k

*

^{— O} 33, k + 1 ,

° i/ , k =^а * , k + 1 , ⁱ , ^j = ¹, ², ³ , боковых поверхностях смежных слоев:

k — 1, 2, ..., K ;

I I o_lljt(1 + e nt) + о₁₂^ —e_12jt 11, k         11, k         12, k        12, k

—

* I

" 33, k I ^O 11, k ,

_ * I  1 *     ,  о *     I _*                 \

^О 11, k I "2" e 12, k ⁺ " 33, k ) ^{+ О} 12, k ^{(1 +} e 22, k ) = ° 12, k ,

*

^O 11, k

e

*

^O 22 k

2 ¹

1 . e

*

' 13, k

*

' 23, k

—

* I * " 22, k I ^{+ O} 12, k

e

—

n * I .     *

" 11, k I ^{+ O} 12, k

1 e

2 ¹

*        . rx*        I .      *

'23, k ⁺ " 11, k I ^{+ O} 13, k

*        . rx*        I .      *

' 13, k ⁺ " 22, k I ^{+ O} 23, k

^O 13, k ,

^O 23 k .

Для решения системы уравнений (6)-(12) выберем в качестве неизвестных функции, с по-

мощью которых выражаются условия контакта между слоями.

Компоненты тензоров деформаций, а также слагаемые, содержащие величины углов поворота в уравнениях (12), определяются с помощью известных соотношений нелинейной теории упругости [2]. Решая систему (6)-(8) относительно этих функций, получаем для ортотропной цилиндрической оболочки следующую разрешающую систему уравнений:

да.

*

*

—

д x ₃

—а

x ₃

—

A ^*

да

*

*

—

—

д ² и

*

x ₃ д x ₁ д x

(А

*

2 ,1 1

да

*

—

д ² и,

д x ₁

д x

^{( А} 1,11 ^{+ а} 11,о

)

—

—

г

1 д ² и

*

x ₃ ² д x 2

^{( А} 3,12 ^{+ а} 22,о

)

—

д x ₃

— а

x ₃

—

*

д ² и

*

д x

(А

*

3,12

1 д

—

да

*

д x ₃

+

1 д и

x 3²

Напряжения

нений (7), (8):

*

а 11

*

а ₂₂

^А 3,12 )

2*

^{+р X и} ₁

—

—

А

*

д и

*

—

X и ₁

x ₃

2,11

д x

—

A

*

2,11

—

д и ₁

к

д T

д x ₁

—

X 1* +

к

t = о

д t    t = 0 ,

1 _A

x ₃

^{+ а} 11,0 )

—

*

1,22

x ₃

u

*

x 2 д x

да

*

—

д x ₁

*

д x ₂

(А

*

*

(А

*

2,22

2,22

*

да

*

—

д ² и

*

д x

д ² и

*

д x

x ₃ д x ₁ д x

(А

*

2,22

+а

(А

22,0

*

1,22

)+

+

^А 3,12 )

тг а

x ₃

22,0

u

*

—

—

+ 2 а

+р X и.

—

*

—

22,0

X и ₂

к

да

*

x ₃

к

д x ₂

+

а

+а

22,0

+А

*

2,22

+р X и

д и

— = a 55 ^а 1

д x ₃

*

—

*

*

к

—

д и

*

д x ,

д и ^*

—- = т,

д x ₃

^а 11 ,

^а 12 ,

*

*

1 1,33 ^а 33

*

+ n 1,33

*

*

= А

= А^:

*

1,11

*

1,22

д и

*

^а 23

) — ~ A x ₃

t = о

*

—

—

A

*

*

д T

2,22

—

д x

д и ₂

д t

1,22

а

*

к

t = о

—

,

А

*

д и

*

1,22

x ₁

X 2^* +

—

A

*

2,22

T | +

^и 3* )

X и ₃

—

а

11,0

—

t = о

д 2 и

*

дx.

д и ₃

д t

д и ^*

— = а 44 а.

д x ₃

д и *

—^L +-- n.

*

—

тг а

x ₃

22,0

*

*

к

,

t = о

Г

*

+-- ^и 2

x ₃

к

д 2 и

*

дx-

—

X ₃ * +

д и

—

*

^д x 2 7

,

д x ₁

x ₃

2,33

д и *2 к и 3 +     + т.

*

*

к

^д x 2 7

2,33

T .

определяются с

u 1

—L + —А

д x ₁

x ₃

*

2,11

а ₁₂

*

*

ди * 1 ,, —^L + — А.

*

г

*

помощью физических и геометрических урав-

u ₃

к

=а

*

д x ₁

x ₃

2,22

д и ^* + —²

д x ₂

г

—

а 33

*

( a B ^А 1   ⁺ a 2з ^А 2,11 ) ⁺ AV ,

3,12

u ₃

к

*

1 д и

*

_к x ₃ д x ₂

д и * к

⁺ I ,

дx, )

д и ^* + —²

д x ₂

—

а ₃₃

*

( ^а 13 ^А 1,22 ⁺ a 23 ^А 2,22 ) ⁺ Т >,22 ^T "

Коэффициенты в уравнениях (13) и (14) определяются следующими соотношениями между физико-механическими и теплофизическими параметрами слоев оболочки корпуса летательно-

го аппарата:

*      a 22 a 66     *       a 12 a 66     *       a 12 a 66

‘ 1,11                ^{; А} 2,11                ^{; А} 1,22                ^;

’ А         ’ А ’ А

**        **2*

*    _ a ll a 66 . д*    _ a ll a 22    ( a 12 ) .

‘2,22         . *    ; А3,12                . *

,А ,

*    *   *     **     *      **     *  *     *      **    **      *        *       *

‘ — ^a 66 |_ а_и   ( ^a 22) J ; Дд ^—   a ₁₃ ^A ₁ , ₁₁    ^a 23 ^А 2,_П ; A 1,22 —   a 13 ^A 1,22    ^a 23 ^А 2,22 ;    A 2,11 ^— -°⁽ 11 ^А 1,11   ° 22 ^А 2,11 ;

*       *      *     *    **    **

’,22 ^— - ^а 11 ^А1 ,22   ° 22 ^А 2,22 ^;   n 1,33 ^{— a} 13 ^A 1,11 + ^a 23 ^А 1,22 ^;

*   **   **

n 2,33 ^{— а} 13 ^A 2,11 + ^a 23 ^A 2,22 ^;

*      **    **     *        *           *         *

m 1,33 ^— - 13 n i,33   ^a 23 ^A 2,зз + ^a 33 ;       ^m 2,33 ^{—  a} 11 n 1,33    ^a 22 n 2,33 + ^a 33 ;

* 1 *	*         1 *	* 1 *	* _ V12 .	* — V13 .	* _ V23 .
a 11 — 73  ; E 11	a 22 —      ; E 22	a 33 —       ; E 33	a 12       73    ; E 22	a 13       73    ; E 33	a 23       33   ; E 33

a

*

1 _;

G 23

*

^a 55 ^—

1 _;

G 13

*

^a 66 ^—

G 12

Представим неизвестные функции g*, а также параметры нагрузки g± в виде двойных тригонометрических рядов:

М М

* _*    ±               *    _*     _± u1 , g13, с13 } — ^^{ u1, mn , g13, mn , g13, mn } cos , x1 cos nx 2 , m—1 n—0

M M

* _*    ±               *    _*     _±

u 2, g23, g23}—^^{ u 2, mn , g23, mn , g23, mn } sin , x1 sin nx 2 , m—1 n—0

мм,

* _*    ±               *    _*     _± u3, с33, с33}— ^^{u3,mn , ^33,mn , ^33,mn } sin , X1 cos nx2 ;

m—1 n—0

±

^С 13, mn

±

^С 23, mn

±

^С 33, mn

l 2 п

± mп t — I I с13 cos—x1 cos nx2dx1 dx2, 00

l 2 п

± m п

— I I c23 sin—x1 sin nx2dx1 dx2, l 2п

± m п

, — I I с ₃₃ sin— x ₁ cos nx ₂ dx ₁ dx ₂ .

Производные по времени разложим в конечные разности с шагом А t :

д2с* — 2ct* (ts) - 5a*(ts-1) + 4g*(ts-2) - a*(ts-3) dt2                           А t2                       , da* — 3g*( ts)- 4g*( ts-1) + g*( ts-2) dt                 2А t              "

Подставим разложенные в ряды (16) и конечные разности (18) искомые функции g* в разрешающую систему уравнений (13). Получим систему обыкновенных дифференциальных уравнений для каждого временного шага ts и каждой пары волновых чисел m и n разложения в двойные ряды Фурье соответственно по продольной х1 и окружной x2 координатам:

*и

---,  ' -        ' - A111A m 533( ts ) + U1 (ts ) (A1,11A m + ~ A3,12 + 5 |Am + оx3           x3                                '           x3

, n _    \ n ~          a *    , A*   \   ¹ ~ M*

+ 2 ^ 22,0 )       ^ m u 2⁽ t s ^{) (A} 2,11 + ^A 3,12 )       ^ m u 3⁽ t s ^{) A} 2,11

- A2,11V(ts) - x 3         x 3

• ^- X 1 ⁽ t s ) *      • ^{[ 2} u 1 ⁽ t s ) ^{- 5} u 1 ⁽ t s - 1 ) ^{+ 4 u} 1 ⁽ t s - 2 ) ^{- u} 1 ⁽ t s - 3 ^{) ]} ;

A t ²

d5A(ts )     2сз(ts )   nn

'     =+ — A1,22533 (ts )AmU (ts ) ( A1,22 + A3,12 ) + dx3            x3       x3                x3           x'

3/A * У 2 , n2 A*     , _ У 2 , n2 _      , 1 _\ ,

+U2(ts ) (A3,12Am +  2 A2,22 + 511,0Am +  2 522,0 +  2 522,0 ) + x3                     x3

n *

⁺    Т^ю( t s ) ^{( A} 2,22 ⁺ 2 ^ 22,0 ) ^{+     A} 2,22 ^{T (} t s ) -

x

* Z X p Г «.   * z x -  * z x .   * z x * z xl

• ^{- X} 2 ⁽ t s ) ⁺ .    ^{[ 2} u 2 ⁽ t s ) ^{- 5 U} 2 ⁽ t s - 1 ) ^{+ 4 U} 2 ⁽ t s - 2 ) ^{- U} 2 ⁽ t s - 3 ^{) ]} ;

A t ²

A⁵^ t s )

5 x₃

_ У G    ⁵ 23 ⁽ ts )„.

- Am5'3< ts )          n + x3

^ 33 ⁽ ts ) / A*

⁽ A 1,22 x 3

*

- 1) - -A^ Xm U 1 (t s ) + x ₃

n *

+— uU x ₃

( t s ) ( A 2,22

⁺ ^ 22,0 ) ^{+ U} 3 ⁽ t s )

( 1 .

- A 2,22

( ^x 3

У ₂     1         ₂ |    T ( t s ) a*

+ ^11,0Xm +   2 ^22,0n  I +        A2,22 - x3        J    x3

• - r^ *z x         ^P Г * Z X „  * X X ,   * z x        * z        xl

• ^- X 3⁽ t s ) + 727^{[ 2 U} 3 ⁽ t s ) - ^{5 U} 3 ⁽ t s - 1 ) ^{+ 4 U} 3 ⁽ t s - 2 ) - ^U 3 ⁽ t s - 3 ^{) ]} ;

A t ²

**

^{d u} 1 ^{( t}s ) __n**(_t 43          .   ^{d U} 2 ⁽ ts )

^{— а} 55 С 13 ⁽ t s )   A, m ^u 3 ^{( t} s ) ;

o x ,                               d x ₃

*   */,\.  ¹   */,\ . n * /, \ .

^— a 44 ^ 23 ⁽ ts ) ^{+      U} 2 ⁽ ts ) ^{+      U} 3 ⁽ ts ) ;

x ₃

x ₃

Ci u ^{( t} )      *    * , ,      * Г A n A A , ,     ¹ A A , , A , ,

—- ^— m 1,33 ^ 33^{( t} s ) - n 1,33 ^A m U ^(t s ) +- n *,33 u 2^{( t} s ) ■    n 2,33 u *^{( t} s ) ⁺ m *,33 ^T(t s ) .

Решение системы уравнений (19) осуществляется численным методом дискретной ортогонализации [3], который позволяет автоматически удовлетворять граничным условиям контакта слоев оболочки. Статическое напряженно-деформированное состояние оболочки, обусловленное постоянными или медленно изменяющимися нагрузками в процессе эксплуатации, определяется с помощью методов расчета наследственной ползучести [1]. При воздействии динамических нагрузок на рассматриваемую оболочку корпуса, полученные значения с110 и с22 0 , характеризующие предыдущее статическое состояние конструкции, используются в качестве параметров предварительного нагружения в уравнениях (19). Результатом решения системы уравнений (19) являются функции 5*3 mn. Искомые функции 5*3 определяют с помощью выражений (16) путем двойного суммирования о*3 mn. Оставшиеся искомые напряжения 5*1, 5*., 523 находят также путем двойного суммирования результатов разложения этих функций, определяемых уравнениями (14), аналогично уравнениям (16):

М to

5*1 — ZZ m-1 n-0

*

4 *   _*       . ^A2,11 / . *             *    \ A * ^ . *

1,11 33, mn            \ 2, mn       3, mn /       1,11 m 1, mn

x sin Amx1 cos nx2,

to to

5 12 - EE

m - 1 n - 0 у

*

^U 2, mn ^A m

—

¹ *        l x

—U 1 _mn n I ^c °s A _m x 1 sin nx ₂ , x ₃ ,     J

to to

5*22 -EE m-1 n-0

*

*             £ 2,22

^Л1,22 ° 33, mn ⁺ x ₃

( *        .    * A A *   ^     *

l/n П + Us — А, АпЛ w, 2, mn       3, mn       1,22 m 1, mn

sin A _m x 1 cos nx ₂ .

Блок-схема алгоритма решения задачи приведена на рисунке. На первом шаге осуществляется ввод данных о массово-геометрических, физико-механических, теплофизических и деформационных характеристиках материалов и конструкции корпуса летательного аппарата. На втором шаге определяются коэффициенты, учитывающие данные свойства материалов и конструкции, с помощью соотношений (15). Одновременно на шаге 3 выполняется операция задания нагрузки, действующей на конструкцию, выраженной через наружные и внутренние напряжения, перемещения и температуру. Заданные составляющие функций параметров нагружения используются для определения коэффициентов пошагового разложения нагрузки по волновым числам m и n в меридиональном и окружном направлениях соответственно. Для этого используются двойные интегральные выражения для коэффициентов анализа Фурье (17). Далее, на шаге 5 с помощью выражений (16) определяются функции разложения нагрузки и параметров напряженно-деформированного состояния в двойные тригонометрические ряды.

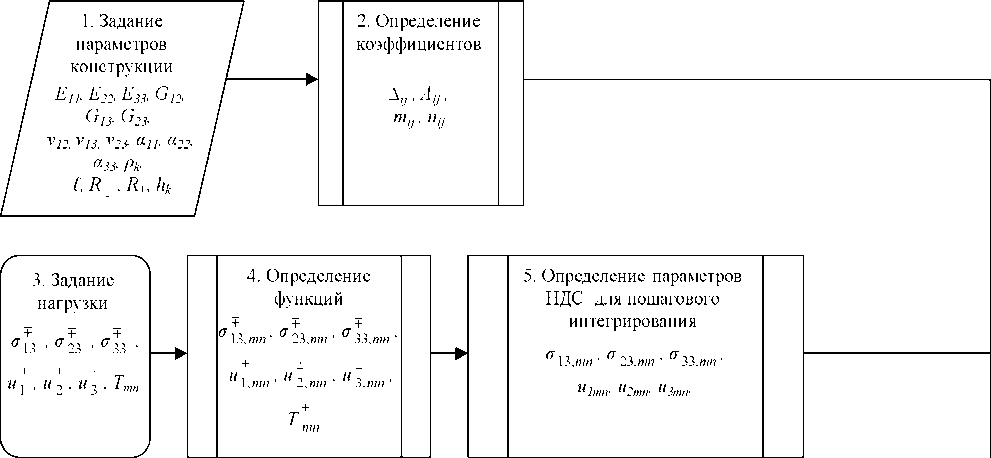
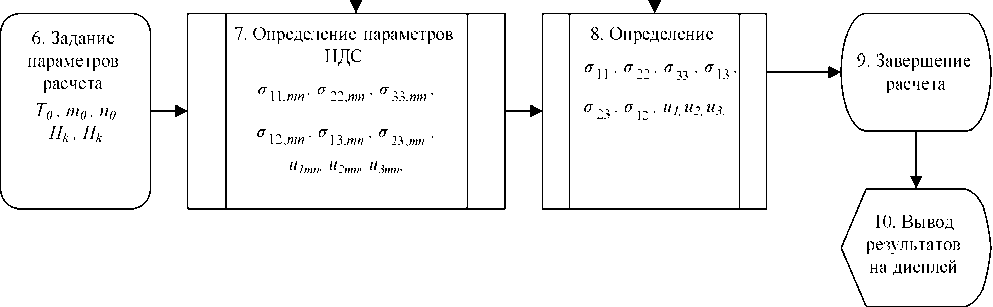
Блок-схема решения задачи

На шестом шаге алгоритма задаются параметры численного интегрирования (начальные значения температуры, волновые числа, число шагов интегрирования по толщине каждого слоя и число точек дискретной ортогонализации). На шаге 7 выполняется решение системы обыкновенных дифференциальных уравнений (19). На шаге 8 определяются искомые полные функции напряжений и перемещений путем двойного суммирования волновых функций (20). Для решения уравнений (19) и (20) используются результаты, полученные на шагах 2, 5 и 6 алгоритма, как показано на блок-схеме (см. рисунок).

Системы уравнений (6)-(20) и рассмотренные методы их решения могут быть использованы для решения физически нелинейных задач термоупругости и термовязкоупругости при многофакторном статическом и динамическом нагружении многослойных оболочек сложных несущих конструкций летательных аппаратов из полимерных композитов в условиях эксплуатации.

Заключение. Представлена математическая модель для анализа сложного напряженно-деформированного состояния многослойных несущих конструкций летательных аппаратов. Решение системы уравнений осуществлено комплексным многоуровневым методом, позволяющим учесть особенности геометрии конструкции и поведения конструкционных материалов при многофакторном нагружении.