Многоуровневый оптимизационный подход к управлению развитием иерархических социально-экономических систем

DOI:

Существующая система управления на различных уровнях (государство, округ, субъект Российской Федерации, муниципальное образование, хозяйствующий субъект) подразумевает необходимость согласования принимаемых управленческих решений, позволяющих обеспечить достижение как стратегических, так и тактических целей, направленных на устойчивое развитие РФ и повышение качества жизни населения. Сложность управления такой системой, которую будем называть иерархической социально-экономической системой (далее – ИСЭС), заключается в наличии множества межуровневых и внутриуровневых связей как между субъектами, так и между объектами управления, что требует планомерной трансформации традиционных методов управления и их интеграции с современными достижениями науки в области информатизации и математического моделирования. Неслучайно в подавляющем большинстве регионов РФ используются различные информационные системы, позволяющие упростить взаимодействие соответствующих органов с целью оптимизации процедур согласования решений различного уровня. Однако в качестве ключевого метода используется метод экспертных оценок, отодвигая на второй план разрабатываемый для этих целей математический аппарат и различные методы моделирования, последние из которых позволяют обосновать и ускорить процесс принятия решений на различных уровнях.

В этом аспекте актуальным представляется концептуальное и формализованное описание такого процесса, включающего характеристику ИСЭС, конструирование индикаторов ее оценки различного типа, а также использо- вание этапов анализа и синтеза управленческих решений в рамках новой теории экономических систем для обеспечения заданных (желаемых) результатов функционирования объекта исследования, представляющего собой иерархическую структуру.

Целью исследования является разработка многоуровневого оптимизационного подхода к управлению развитием ИСЭС.

Состояние проблемы и обзор исследований

Современные концептуальные и формализованные описания иерархических социально-экономических систем базируются на классических работах Т. Саати [Саати, 1993] и М. Мексаровича [Месарович и др., 1973], в которых введены такие понятия, как «иерархия», «уровень», «страта», «слой», и которые позволяют выделить иерархические системы среди остальных структур и формально их описать в терминах теории множеств. На базе таких структур решается ряд оптимизационных задач, связанных как с оптимизацией иерархических структур [Воронин и др., 2003], так и с принятием оптимальных решений для одного элемента или группы элементов уровня [Андрейчиков и др., 2015] на множестве вариантов по Парето [Ногин, 2002].

В рамках описания иерархических структур должна быть осуществлена классификация элементов, позволяющая объединить их в однотипные группы (классы). Примерами таких классификаций являются: классификация С.В. Белоусовой (общая классификация социально-экономических систем) [Белоусова, 2015]; пространственно-временная классификация Г.Б. Клейнера на базе новой теории экономических систем [Клейнер, 2016]; клас- сификация И.К. Ларионова по типу хозяйственного механизма [Ларионов, 2001] и др. При всем многообразии классификаций, по сути, такая процедура объединения элементов дает возможность «взглянуть» на одну и ту же сложную систему (один и тот же процесс или явление) с той или иной точки зрения, воспринимая совокупность элементов как некоторую подсистему, функционирующую, опять же с точки зрения исследователя, как единое целое. То есть многообразие классификаций определяется целями и взглядами автора, принимающего либо традиционную, либо собственную классификацию, последняя из которых должна быть понятна не только автору, но и другим исследователям. В этом смысле процедура согласования результатов исследований может быть решена за счет введения таблицы (матрицы) сопряженности, устанавливающей соответствие изучаемых признаков в различных классификациях.

В случае если объект исследования идентифицирован: описана его структура (концептуально или формализованно), проведена классификация, то изучение (в данном аспекте – оценка функционирования ИСЭС) можно осуществлять через его признаковые описания, которые, в свою очередь, определяются выбором соответствующих индикаторов, что представляет определенную проблему для исследователя. Многообразие классификаций и целей проводимых исследований порождает множество как частных, так и интегральных (для совокупности элементов ИСЭС) индикаторов оценки. Среди таких индикаторов можно выделить, например: индикаторы устойчивого развития [Человек ... , 2018]; показатели качества жизни населения [Айвазян, 2012]; индикаторы, определяемые по системе национальных счетов [Зандер и др., 2015]; валовой региональный продукт (ВРП, наиболее часто используется в региональных исследованиях при оценке экономической составляющей ИСЭС, а также его модификация – ВРП на душу населения при конструировании индекса состоятельности) [Жуков, 2019г]; показатели оценки функционирования отдельных сфер производства товаров и услуг [Региональная экономика, 2012]; другие макроэкономические показатели [Арженовс-кий и др., 2014; Вероятностная модель ... ,

2016; Черницкий, 2014]. Наряду с традиционными показателями оценки функционирования ИСЭС, могут быть использованы частные и интегральные показатели результативности, эффективности и гармоничности, обоснование применения которых отражено, например, в [Жуков, 2019в].

Наличие индикаторов оценки позволяет сравнивать заданные (нормативные, ожидаемые) результаты функционирования ИСЭС с их фактическими значениями, обеспечение соответствия которых друг с другом является основной задачей управления на различных уровнях иерархии. Следовательно, для решения этой задачи (управление развитием иерархических социально-экономических систем) необходимо сформировать такие условия за счет воздействий со стороны субъекта управления, которые бы позволили достигнуть ожидаемых результатов – целей функционирования объекта исследования. Формализация задачи управления, причем наиболее оптимальным (эффективным) способом, предопределяет необходимость построения как моделей самой ИСЭС (например, с использованием классических производственных функций [Cobb et al., 1928; Solow, 1956; Corbo et al., 1979]), так и модели управления на разных уровнях иерархии. Становление системы взглядов на процесс управления сложными системами, обзор которых представлен в [Формирование ... , 2018], обусловливает необходимость использования как технико-экономического, так и традиционного (классический менеджмент) подхода к управлению ИСЭС в рамках общей теории систем и системного анализа [Bertalanffy, 1962].

Этапы подхода

Разработанный многоуровневый оптимизационный подход к управлению ИСЭС предполагает реализацию следующих этапов: 1) формализованное описание ИСЭС; 2) идентификация результатов функционирования ИСЭС на каждом из уровней иерархии, а также факторов состояния и воздействия (управляющих факторов), характеризующих конкретные условия деятельности объекта исследования; 3) построение моделей связи между результативными признаками элементов (классов, уровней) ИСЭС и условиями, по ко- торым определяются нормативные (ожидаемые) значения, являющиеся целью функционирования ИСЭС; 4) оценка показателей результативности, эффективности и гармоничности функционирования ИСЭС, однотипных для каждого из иерархических уровней; 5) отбор результативных признаков, не соответствующих нормативным значениям; 6) оптимизация факторных признаков – поиск таких значений, при которых рассматриваемые результативные признаки, характеризующие функционирование элементов, классов, уровней и ИСЭС в целом достигали бы (находились в допустимых пределах) своих нормативов, то есть цели функционирования были бы достигнуты. Заметим, что значения нормативов в случае их задания для нескольких временных периодов можно ассоциировать (связать) с заданной траекторией развития ИСЭС.

По сути, последний этап представляет собой поиск оптимального решения при управлении развитием ИСЭС, который должен быть включен в соответствующий контур с обратной связью на базе принципа управления по отклонению (компенсации) на каждом цикле принятия решения. Контур управления может быть представлен в виде кибернетической и процессной моделей.

торальному [Колесников, 2016] признакам или – в традиционном варианте – по разделам Общероссийского классификатора видов экономической деятельности (ОКВЭД).

• 2.    Идентификация признаков. Каждый из элементов ИСЭС уровня L_p характеризуется 4 типами признаков (допустимо отождествлять объекты с их признаковыми описаниями): 1) результативный признак y_{p (} p_p -^ s ( t ) - результат функционирования элемента в период времени t , t = 1, ..., T , T – число периодов (фактические значения результативного признака); 2) факторы состояния x _pl^_{p -1} ) j ( t ) - условия функционирования элемента, j = 1, ..., J , J – число факторов состояния; 3) факторы воздействия z p , ( p -, ) , v p , s q , u ⁽ t ) , которые характеризуют управляющие воздействия на элемент, u = 1, ..., U , U – число факторов воздействия; 4) нормативный результативный признак y _p ( _p — i ) _{v s} ( t ) - нормативный (ожидаемый) результат функционирования элемента.

• 3.    Связи. Связи между результативными признаками и факторами состояния и воздействия могут быть представлены посредством неслучайных функций f _{p ,( p –1)} , которые будем называть производственными функциями (далее – ПФ):

y p ^{, (} p ^{-1 )} , ^v p , s q ^{( t} )

= f p ^{, (} p ^{-1 )(} x p ^{, (} p ^{-1 )} , ^v p , s q , j ⁽ t ) z p ^{, (} p ^{-1 )} , ^v p , s q , ^u

Параметры ПФ могут быть найдены с помощью факторного анализа зависимостей из эконометрических уравнений вида

^У p ^{, (} p ^-1 ) , s q     ^У p ^{, (} p ^-1 ) , s q ^{+ E},                      ⁽²⁾

где £ - стохастическая случайная составляющая (в первом приближении предполагается нормальной случайной величиной).

Выражение (1) характеризует внутриуровневые связи элементов ИСЭС. Формализованное описание связей классов может быть представлено в виде агрегированной ПФ:

II

^ ^ r p , i 1 , i 2 , s q ' ^У p , i 1 , v p , s q ⁽ t ) ' y p , i 1 , v p , s q ⁽ t ^{) t} , , =1 i 2 =1

где r _p - _{i2 s} - значения парного коэффициента корреляции Пир сона между i ₁ -ми y _p , i , _s и i 2 -ми y _p , , ₂, ^ переменными – признаковыми описаниями ( i ₁ , i ₂ = 1, ..., I ).

Межуровневые связи определяются как суммы соответствующих фактических признаковых описаний элементов или классов [например, среднегодовая численность занятых в субъектах РФ и в округе (сумма занятых во всех субъектах РФ, входящих в состав округа)].

Модели в форме (1) и (3) строятся по статистическим данным для совокупности v_p -х элементов, принадлежащих одному элементу (соотношение (1)) или одному классу (соотношение (3)). Примером таких данных могут служить статистические данные для 17 регионов Центрального федерального округа за несколько периодов времени. Если строить модель из набора частных и агрегированных ПФ только по данным одного региона (например, Тульская область), то такая модель ~р( _{p -1) V} J ( t ) (обозначим такие модели знаком «~», в том числе для обозначения и других индикаторов, которые вычисляются только по данным для одного v_p -го субъекта) будет характеризовать функционирование только исследуемого субъекта РФ и будет выступать уже не в качестве модели для расчета норматива, а в качестве модели для вычисления фактических значений результатов его функционирования с определенной степенью точности, заданной этой моделью. С этих же позиций построенная модель будет характеризовать ожидаемое (нормативное) значение для всех подсистем (МО или хозяйствующих субъектов), входящих в состав рассматриваемого региона (для этого достаточно подставить фактические значения факторов состояния и воздействия конкретного МО).

В этом и состоит одна из особенностей подхода, заключающаяся в построении двух типов моделей: первая – для совокупности однотипных подсистем, вторая – для одной подсистемы. При такой постановке важен выбор точки отсчета – на каком уровне строить базовые модели, а затем по ним определять функционирование элементов (классов) ИСЭС на других уровнях иерархии. Например, строить модели функционирования элементов (классов) для совокупности МО, входящих в состав области, а функционирование области идентифицировать как сумму соответствующих результатов и условий, полученных для муниципальных образований.

В рамках исследования предложено в качестве отправной точки выбрать региональный уровень – мезоуровень, который обладает некоторой общностью имеющихся объектов и процессов, что позволяет использовать ряд моделей в виде производственных функций для описания его функционирования, что согласуется и с идеями А.А. Богданова, которого по праву признают одним из основоположников системного подхода к познанию мира [Богданов, 1989]. Он полагал, что изучение природы вещей следует начинать со среднего – мезо – уровня и через этот уровень искать подходы к пониманию мега-, макро- и микроструктуры мира.

• 4.    Оценка функционирования ИСЭС на разных уровнях иерархии может быть осуществлена с помощью частных и интегральных индикаторов результативности, эффективности и гармоничности, которые формируют систему показателей, позволяющих комплексно изучить объект исследования. Конструирование этих индикаторов подробно отражено в [Жуков, 2019б], и в рамках исследования они имеют опосредованное, хотя и немаловажное значение и выступают в качестве целевых индикаторов в предлагаемом многоуровневом подходе.

В общем виде частные и интегральные показатели результативности можно определить как

^ p ,( p -1), V p , J q ⁽ t ) =

y P ,( p -1), V p , J q ⁽ t )

P                     , yp,(p-1),vp,Jq (t)

^ p , V p , J q ( t ) =

II

V V r . . • y ^P.      ( t ) • y¹

p , i 1 , i 2 , s q y p , i 1 , v p , s q         y

- 1 =1 i 2 =1

( t )

p , i ₂, v_p , s_q

II

EE ^¥P , -„ - 2 , J q • y ^P, 1 , V , , J q ⁽ t ) • y ^P, 1 , V , , J q ⁽ t ), / , =1 i 2 =1

где индекс 0 характеризует, что значения приведены к шкале от 0 до 1 после проведения процедуры стандартизации (случайная величина будет иметь нулевое математическое ожидание и единичную дисперсию, такие случайные величины будем обозначать индексом «*»); r_{p , i , i , s} – значения парного коэффициента корреляции Пи ^q рсона (аналогично (3)).

Если выражения (4) и (5) близки к единице, то можно говорить о соответствии функционирования ИСЭС ожидаемым (нормативным) результатам.

Оценку сбалансированности, в смысле соответствия совокупности показателей результативности нормативным значениям, можно осуществить с помощью коэффициента гармоничности, который определяется по формуле

H Ap ( t )=1

σ(ξ p , i ( t ))

M (ξ p , i ( t ))

где M (ξ _{p , i} ( t )) – математические ожидания; σ(ξ _{p , i} ( t )) – среднеквадратические отклонения; i = 1, ..., Q , Q – число интегральных показателей результативности, соответствующих числу классов.

Чем ближе H_Ap ( t ) к единице, тем более сбалансированно (гармонично) функционирование рассматриваемого объекта исследования.

Набор частных и интегральных показателей эффективности можно представить по формуле

_{Ef ( t ) =} Δ y ( t ) ₌ y ( t ) / y ( t_o )

Δ x ( t ) x ( t ) / x ( t ₀) .

Здесь y ( t ), y ( t₀ ), x ( t ), x ( t₀ ) – соответственно результат функционирования элемента (подсистемы) и его (ее) факторный признак текущего и базисного либо предыдущего периода. Тогда (6) определяет базисные и цепные эффективности. В зависимости от подстановки соответствующих индикаторов в числитель [частный или интегральный показатель результативности (соотношения (4) или (5)) или коэффициент гармоничности] и знаменатель [факторы состояния, воздействия или их комбинации, аналогичные (3)] можно получить систему частных и интегральных показателей эффективности функционирования, воздействия и управления.

• 5.    В качестве критериев, на основании которых принимается решение о необходимости проведения оптимизации, могут выступать частные и интегральные показатели результативности, а также коэффициент гармоничности. Их нормативные значения принимаются равными единице и являются целевыми показателями функционирования ИСЭС:

^^^^

ξp,(p-1),vp,sq(t) =ξp,vp,sq(t) =HAp =1.

Сформируем следующие условия:

ξp,(p-1),vp,sq (t) ∈ ξ p,( p-1),vp,sq (t) ± δp,(p-1),vp,sq (t), ξp,vp,sq(t)∈ξp,vp,sq(t)±δpvp,sq(t),

HAp(t) ∈ HAp(t)-δAp(t), где δp,(p-1),vp,sq (t), δpvp,sq (t) и δAp(t) – соответствующие доверительные интервалы, которые можно задать априорно (1 %, 5 %, 10 % и т. п.) или определить по формуле

δ = t 1-α; n - p -1 ⋅ s ⋅ 1 + Α 0 ^T ⋅ ( Α ⋅ Α^T ) ^{- 1} Α 0 ,       (10)

где t _{1 - α; n - p - 1} – коэффициент, отвечающий за доверительную вероятность траектории; α – уровень значимости; n – число наблюдений; p – число параметров модели; s – среднеквадратическая ошибка модели; A – матрица известных значений факторов состояния и воздействия; A⁰ – вектор ожидаемых значений факторов состояния и воздействия.

Если условия (9) выполняются, то функционирование ИСЭС признается удовлетворительным. В противном случае необходима оптимизация.

• 6.    Процедура оптимизации. Пусть цель на уровне иерархии L_p , p = 1, ..., h определяется некоторым индикатором ξ _p , который является элементом множества признаковых описаний D_g объекта (элемента) k_p (в данном случае индикатор отображает результат функционирования ИСЭС на L_p ). Если элемент множества k_p есть объект, состоящий из совокупности объектов (то есть сам представляет собой некоторое подмножество) k ∈ L , i = 1, ..., N ( N – количество элемен- p , i , q       p                   p p

тов множества на заданном уровне иерархии), сопоставленных с элементами множества наименований (номеров) классов s _q ∈ S , то цель для ∀ k _{p , i , q} можно сопоставить с индикатором ξ _{k , p , q} , который является элементом множества признаковых описаний D объекта ξ k , p , q

• ^kp , i , q ^{∈ L}p , q ^{⊂ L}p ^{, L}p , q ^{→ s}q ^{∈ S} .

Введем функцию ω _p :ξ _{p , q} → ξ _p , q =1, ..., s ( s – число классов), которая будет иметь смысл агрегирования целей k _{p , i , q} на заданном уровне иерархии p . Тогда ξ _p = ω _p (ξ _{p , q} ) будет определять цель на L_p .

В простейшем случае

s

ξ p = ∑ ω p , q ⋅ ξ p , q                 (11)

q =1

где ∑s ωp,q=1 и ωp,q – весовая функция, отражаю-q=1      , щая приоритет относительно цели ξ p,q.

Такое формальное описание позволяет идентифицировать цели моделирования развития ИСЭС для каждого уровня иерархии.

Далее, поставим следующую общую задачу. Требуется найти такие значения приращений факторов состояния А х ,__{n v} „ .( t ) и p ,⁽ p 1), v p , s q , j факторов воздействия A z _p ,_{( p - 1X v} , s , u ( t ), для которых целевая функция (11) и ее составляющие стремятся к единице.

Эта задача может быть сведена к одному из 7 типов задач многокритериальной оптимизации, рассмотренной в [Жуков, 2019а], с тем отличием, что вместо фактических значений результативного признака y p, ( _{p - n v} s (t ) берется значение ~ p ,_{( p} _ ,), _v , s ( t ) , вычисленное по данным только для v_p -го элемента или класса.

Для устранения необходимости придания некоторых значений весовым коэффициентам в (11) с помощью экспертных оценок можно воспользоваться расширением метода, основанным на методологии анализа среды функционирования (АСФ) [Кривоножко и др., 2010], и метода Лагранжа, сформировав целевую функцию в следующем виде (при добавлении в соотношение коэффициента гармоничности в числитель добавляется соответствующее слагаемое с коэффициентом):

F v p ( t ) =

Ц • (~ Pv p , s , ( t ) _ j^, , ( t )) + Z i • (~ P,;v p , s , ( t ) _ y° p,    ( t ))

( p - 1) j        ,                     ( p- 1) и                                   * (12)

ZZ ® i , j>P^q„(tt ) + VV iu jA zp,_w ( t )

== 1 j = 1

* max, i=1 u=1

где μ μ _i ω _{i j} η _{i u} – соответствующие весовые коэффициенты обобщенного и частных показателей результативности а также факторов состояния и воздействия. В данном соотношении приращения факторных признаков будем считать нормализованными то есть приведенными к интервалу от 0 до 1. Числитель представляет собой сумму разностей модельного и нормативного значений для обобщенного и частных показателей результативности v_p -го элемента (класса подсистемы) которые должны стремиться к максимуму. Знаменатель по сути есть требование минимизации затрат на реализацию мероприятий направленных на достижение нормативных значений функционирования рассматриваемой сложной системы.

Аналогично [Жуков 2019а] воспользовавшись методом Лагранжа и преобразованием

Чарнеса и Купера для задач дробно-линейного программирования [Polyhedral ... p. 73] задачу можно свести к следующему виду:

( P -1)

F (t) = Э^ + Z Д * max, i=1

где ϑ _μ ϑ _i – преобразованные от x ⁰ _{p i v s j} ( t ) и z ⁰ _{p i v s u} ( t ) переменные с системой ограничений:

mJmU

ZZu.+ZZu. = 1, i=1 j=1             i=1 u=1

gl (ui,j, Uiu ) = °.

В простейшем случае можно оптимизировать частные показатели результативности по отдельности то есть решать задачи линейного (если производственные функции линейны) и нелинейного программирования с ограничениями. В качестве инструментальных средств можно использовать программный комплекс «ЭФРА» [Программа ...] либо среду разработки Mathlab [Среда ...].

После того как формализован алгоритм поиска оптимального решения строится контур управления в соответствии с предлагаемым многоуровневым оптимизационным подходом в виде кибернетической и процессной моделей.

Кибернетическая и процессная модели управления ИСЭС на основе многоуровневого оптимизационного подхода

В основе многоуровневого оптимизационного подхода лежит одноуровневый подход предложенный в [Жуков 2019б] отличающийся тем что в контур управления вводится дополнительная модель которая описывает функционирование конкретного v_p -го элемента (класса подсистемы) и строится по данным только для этого объекта исследования.

Для наглядности обозначим модели которые строятся по данным для совокупности объектов подчиненных одному элементу (классу) более высокого уровня ( p – 1 ) как ФО-модели (регионы федерального округа) а модели что построены только по данным для v_p -го элемента (класса) как Р-модели (модели функционирования региона (области субъекта РФ)).

Кибернетическая модель представлена на рисунке 1.

Результаты функционирования ИСЭС разделяются на три направления: 1) объем продукции и услуг, который поставляется внешней среде {yi,ext (t)} (где i – индекс продукции или услуг; ext – external; {} – вектор, компонентами которого являются yi,ext (t)); 2) {yi,int(t)} (где int – internal) – результаты, идущие на внутреннее потребление и накопление; 3) информация о результатах функционирования ИСЭС, ее состоянии и характере воздействия в рассматриваемый период. Сбор информации осуществляется через систему мониторинга. Результаты мониторинга сравниваются с данными, полученными по ФО-модели, и попадают в блок анализатора, который вычисляет целевые индикаторы: показатели результативности, эффективности и гармоничности, которые вычисляются с использованием результатов оценки по Р-мо-дели и ФО-модели [данные подставляются соответственно в числитель и знаменатель соотношений (4) и (5)]. На данном этапе субъект управления осуществляет корректировку Р-модели с учетом вновь появившихся данных. В блоке формирования управляющих воздействий осуществляется процедура оптимизации в соответствии с целями субъекта управления, имеющимися расхождениями между результатами оценок по Р- и ФО-моделям (этапы 5 и 6 многоуровневого оптимизационного подхода), результатом реализации которого становятся рекомендации в части изменения факторов состояния и воздействия с учетом ограничений на внутренние и внешние ресурсы, позволяющие достигнуть нормативных (ожидаемых) значений результатов функционирования ИСЭС. Эти рекомендации используются для организации деятельности ИСЭС в следующем цикле.

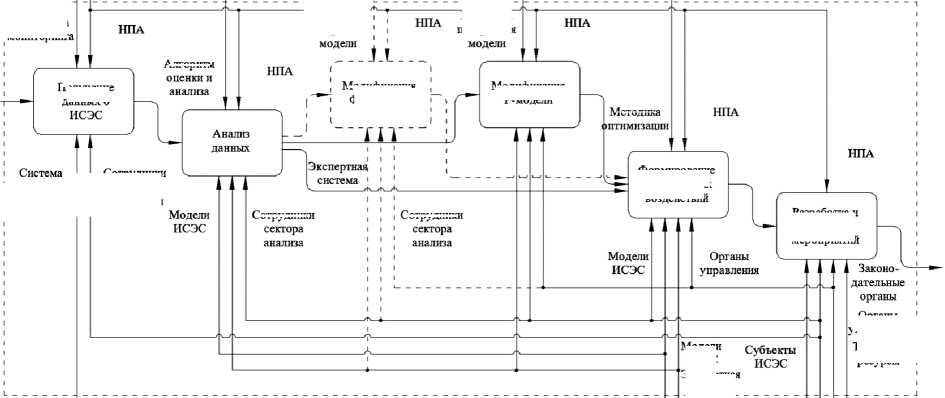
Процессная модель в нотации IDEFX демонстрирует связь этапов цикла управления, используемых ресурсов и информации, обеспечивающих реализацию каждого из этапов (см. рис. 2).

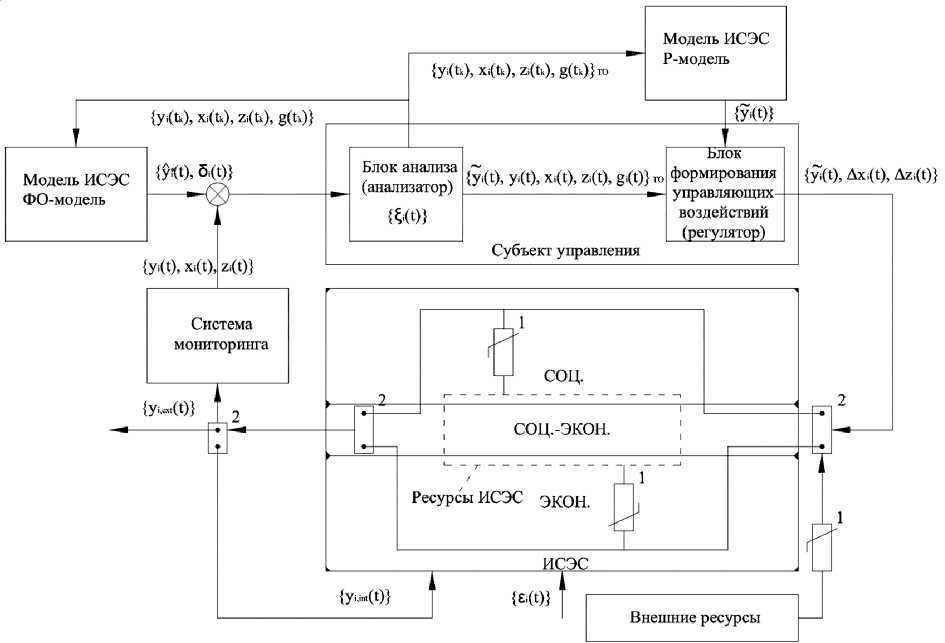
Рис. 1. Кибернетическая модель управления состоянием и развитием ИСЭС: 1 – ограничитель; 2 – разделитель

Примечание. Составлено автором.

Программа мониторинга

Методика । построения 1

Методика построения мониторинга

Алгоритм

Методика

Сотрудники

Сотрудники управления

Получение данных о

Рис. 2. Процессная модель управления состоянием и развитием ИСЭС Примечание. Составлено автором.

Модификация ФО-модели

Модификация Р-модели

Сотрудники сектора статистики

Формирование управляющих воздействий

Разработка и реализация мероприятий

Модели исэс

Экспертная система

Органы управления Трудовые ресурсы

Отличительной чертой процессной модели будет необходимая модификация Р-моде-лей на каждом цикле управления с учетом вновь появившихся данных.

Особенность данного подхода заключается в использовании двух типов моделей. Модели, относящиеся к первому типу, применяются для формирования нормативов и траектории развития (устойчивого развития), а модели, принадлежащие второму типу, – для поиска оптимальных значений факторов состояния и воздействия. Корректировка ФО-моделей (на рисунке 2 обозначено пунктирной линией) осуществляется не в каждом цикле, а в случае принятия решения об изменении нормативных (ожидаемых, плановых) показателей (целевых индикаторов), которые регламентируются, например, программой социальноэкономического развития субъекта РФ. Для повышения качества моделей и идентификации неучтенных факторов необходимо увеличить объем выборки, в том числе за счет разделения региона (области) на муниципальные образования и сбора данных по ним.

Однако, по крайней мере, на данном этапе это представляется серьезной проблемой, связанной с организацией статистических исследований, а также с раскрытием информации, определяемой федеральными законами Российской Федерации «Об информации, информационных технологиях и о защите информации» [Федеральный закон РФ от 27.07.2006 ...], «О го- сударственной тайне» [Федеральный закон РФ от 21.07.1993 ...] и «О коммерческой тайне» [Федеральный закон РФ от 29.07.2004 ...]. Именно поэтому в рамках исследования Р-модель строится по данным только для региона, а не по данным для совокупности МО, входящих в его состав.

Аналогичные модели управления будут характерны и для других уровней иерархии.

Заключение

В исследовании представлен многоуровневый оптимизационный подход к управлению развитием иерархических социально-экономических систем, заключающийся в использовании математического аппарата при принятии управленческих решений и позволяющий снизить влияние субъективизма со стороны лиц, принимающих решения. Он включает в себя: 1) концептуальное и формализованное описание объекта исследования (ИСЭС); 2) набор моделей 1-го типа, представленных в виде частных и агрегированных ПФ, которые используются для формирования нормативов – целевых значений индикаторов для элементов и подсистем, подчиненных только одному из элементов (подсистем) более высокого уровня; 3) набор моделей 2-го типа, строящихся только по статистическим данным одного элемента (подсистемы) заданного уровня ИСЭС, которые используются при проведении процедуры оптимизации – поиска таких факторов состояния и воздействия, при которых бы рассматриваемые элементы (подсистемы – классы, уровни, ИСЭС в целом) смогли достичь заданных (нормативных, ожидаемых) целевых значений индикаторов.

В рамках исследования построены кибернетическая и процессная модели управления развитием ИСЭС, являющиеся одними из составляющих предложенного подхода и позволяющие визуализировать и в дальнейшем реализовать алгоритм управления с помощью некоторых инструментальных средств поддержки принятия решений. В настоящее время такая работа проводится за счет расширения возможностей авторской экспертной системы «ЭФРА».