Множественная линейная регрессия и многомерные модельные распределения при оценке единых объектов недвижимости

Автор: Ласкин Михаил Борисович

Журнал: Имущественные отношения в Российской Федерации @iovrf

Рубрика: Экономика и управление народным хозяйством

Статья в выпуске: 6 (249), 2022 года.

Бесплатный доступ

В статье рассмотрены проблемы, связанные с расчетами оценок рыночной стоимости единых объектов недвижимости как комплексов, включающих объекты капитального строительства и земельные участки, на которых они находятся. Показаны возможные пути решения таких проблем при помощи построения моделей множественной линейной регрессии с преобразованием ранговых переменных в индикативные, а также с использованием многомерных модельных распределений вещественных переменных. Представлены примеры применения таких расчетов. Показано, что рыночная стоимость единого объекта недвижимости может не быть простой суммой рыночных стоимостей земельного участка и расположенных на нем улучшений и может содержать компоненты стоимости, учитывающие не только площади, но и эффект их взаимосвязи.

Еще

Единый объект недвижимости, множественная линейная регрессия, многомерные распределения, корректировка цен объектов сравнения, преобразование ранговых переменных в индикативные, многомерные модельные распределения вещественных переменных в оценке

Еще

Короткий адрес: https://sciup.org/170196023

IDR: 170196023 | DOI: 10.24412/2072-4098-2022-5248-7-19

Текст научной статьи Множественная линейная регрессия и многомерные модельные распределения при оценке единых объектов недвижимости

Уравнение (10), связывающее цену объекта с площадями ОКС и земельного участка, принимает вид:

V = exp (2, 6364) x S0y3016 x S0;7055 = 13, 97 x S30y3016 x S0^l55. ОУ OnC ОУOnC

Формула для расчета удельной стоимости на единицу площади ОКС:

-V- = 13, 97 x S033016 x S . 2445.(1 1)

SOKC

Формула для расчета удельной стоимости на единицу площади земельного участка:

— = 13, 97 x S306984 x S0,7C555 ' ОУOn C

S3V

По приведенным формулам могут быть рассчитаны таблицы значений РС объекта оценки (табл. 3), удельная стоимость на 1 квадратный метр ОКС (табл. 4), удельная стоимость на 1 квадратный метр земельного участка (табл. 5) в зависимости от значений предикторов – площади ОКС и площади земельного участка.

Теперь рассмотрим случайный вектор ( V , S_ЗУ , S_ОКС ) (этот кейс был подробно рассмотрен в работе [1], данные протестированы на совместную нормальность логарифмов компонент, там же выведены необходимые формулы). Итоговые формулы выглядят несколько громоздкими, но основная идея проста. Сначала вместо случайного вектора ( V , S_ЗУ , S_ОКС )

Таблица 3

Результат оценки РС ЕОН в зависимости от площадей ЗУ и ОКС, тыс. р.

		Площадь земельного участка, кв. м
		2 000	7 000	12 000	17 000	22 000	27 000	32 000	37 000	42 000	47 000
>3 Ф 9 M -fl 5с Ъ <Х$ 9-о 5	400	12 783	18 652	21 945	24 376	26 347	28 025	29 499	30 819	32 020	33 125
	2 400	49 492	72 215	84 962	94 373	102 005	108 504	114 209	119 321	123 970	128 248
	4 400	78 238	114 158	134 309	149 186	161250	171 524	180 542	188 623	195 973	202 735
	6 400	103 838	151 512	178 257	198 002	214 013	227 648	239 618	250 343	260 098	269 073
	8 400	127 521	186 068	218 912	243 160	262 823	279 569	294 268	307 439	319 419	330 441
	10 400	149 850	218 649	257 245	285 738	308 844	328 522	345 795	361 272	375 351	388 302
	12 400	171 146	249 723	293 804	326 347	352 737	375 211	394 939	412 616	428 695	443 487
	14 400	191 615	279 589	328 943	365 378	394 924	420 086	442 173	461 965	479 967	496 528
	16 400	211 398	308 455	362 904	403 101	435 698	463 458	487 825	509 660	529 521	547 792
	18 400	230 599	336 471	395 865	439 713	475 271	505 552	532 132	555 950	577 615	597 546

Таблица 4

Результат оценки удельной РС ЕОН, в тыс. р. на 1 кв. м площади ОКС в зависимости от площадей ЗУ и ОКС

		Площадь земельного участка, кв. м
		2 000	7 000	12 000	17 000	22 000	27 000	32 000	37 000	42 000	47 000
>3 CD э I^s-s со га о ё	400	31,958	46,631	54,862	60,939	65,867	70,064	73,747	77,048	80,051	82,813
	2 400	20,622	30,090	35,401	39,322	42,502	45,210	47,587	49,717	51,654	53,437
	4 400	17,781	25,945	30,525	33,906	36,648	38,983	41,032	42,869	44,539	46,076
	6 400	16,225	23,674	27,853	30,938	33,440	35,570	37,440	39,116	40,640	42,043
	8 400	15,181	22,151	26,061	28,948	31,289	33,282	35,032	36,600	38,026	39,338
	10 400	14,409	21,024	24,735	27,475	29,697	31,589	33,249	34,738	36,091	37,337
	12 400	13,802	20,139	23,694	26,318	28,447	30,259	31,850	33,275	34,572	35,765
	14 400	13,307	19,416	22,843	25,373	27,425	29,173	30,706	32,081	33,331	34,481
	16 400	12,890	18,808	22,128	24,579	26,567	28,260	29,745	31,077	32,288	33,402
	18 400	12,533	18,286	21,514	23,897	25,830	27,476	28,920	30,215	31,392	32,475

Таблица 5

Результат оценки удельной РС ЕОН в тыс. р. на 1 кв. м площади ЗУ в зависимости от площадей ЗУ и ОКС

Площадь земельного участка, кв м 2 000 7 000 12 000 17 000 22 000 27 000 32 000 37 000 42 000 47 000 >3 3 CD 9 1» со ■fl ^ 'О га 9 о 5 400 6,392 2,665 1,829 1,434 1,198 1,038 0,922 0,833 0,762 0,705 2 400 24,746 10,316 7,080 5,551 4,637 4,019 3,569 3,225 2,952 2,729 4 400 39,119 16,308 11,192 8,776 7,330 6,353 5,642 5,098 4,666 4,314 6 400 51,919 21,645 14,855 11,647 9,728 8,431 7,488 6,766 6,193 5,725 8 400 63,760 26,581 18,243 14,304 11,947 10,354 9,196 8,309 7,605 7,031 10 400 74,925 31,236 21,437 16,808 14,038 12,167 10,806 9,764 8,937 8,262 12 400 85,573 35,675 24,484 19,197 16,034 13,897 12,342 11,152 10,207 9,436 14 400 95,808 39,941 27,412 21,493 17,951 15,559 13,818 12,486 11,428 10,564 16 400 105,699 44,065 30,242 23,712 19,804 17,165 15,245 13,775 12,608 11,655 18 400 115,299 48,067 32,989 25,865 21,603 18,724 16,629 15,026 13,753 12,714 рассматривается случайный вектор (W, Y, Z), где W = ln(V), Y = ln(SЗУ), Z = ln(SОКС), компоненты которого тестируются на совместную нормальность. Если в результате проверки нулевая гипотеза о совместной нормальности компонент не отвергается, то оценка РС может быть построена по условному распределению случайной величины V при фиксиро-

ванных значениях S_ЗУ = s_ЗУ , S_ОКС = s_ОКС .

Кроме того, для фиксированного значения случайной величины V = v по условному двумерному распределению может быть построено множество всех значений S_ЗУ , S_ОКС, соответствующих такому значению V = v.

В приведенных далее формулах содержится ряд обозначений, аналогичных обозначениям, примененным в работе [1].

Введем вспомогательные обозначения.

Вектор средних случайного вектора ( W , Y , Z ) обозначим ( μ _W , μ _Y , μ _Z ) . Ковариационную матрицу запишем в следующем виде:

CV = ^⎜_⎜ ρ _YW σ _W σ _Y ⎝ ^ρ ZW ^σ W ^σ Z

^ρ WY ^σ W ^σ Y ^ρ WZ ^σ W ^σ Z

^σ Y ² ^ρ YZ ^σ Y ^σ Z

^ρ ZY ^σ Y ^σ Z ^σ Z ²

2 σ _W

cov ( W,Y

COV = ^Y ⎝ ρ _ZY σ _Y σ _Z

^ρ YZ ^σ Y ^σ Z ⎞ σ _Z 2 ⎟_⎠

cov ( W,Y )

COV

где Y = ( Y,Z ) ; cov ( W,Y ) = ( ρ _WY σ _W σ _Y ; ρ _WZ σ _W σ _Z ) ; σ _W ², σ _Y ², σ _Z ² – дисперсии случайных величин W , Y , Z ;

ρ _WY = ρ _YW , ρ _WZ = ρ _ZW , ρ _YZ = ρ _ZY – соответствующие коэффициенты корреляции.

Для оценки РС по условному распределению при заданных значениях S_ЗУ = s_ЗУ, S_ОКС = s_ОКС необходимо знать условное математическое ожидание случайной величины W :

E ( W|Y = y,Z = z ) = μ W +

COV -1 x cov ( X,Y ) T , ( y - ^.z - ^ z )

и условную дисперсию случайной величины W :

D ( W | Y = y,Z = z ) = 0 ^ 2, - COV "1 x cov ( w.^Y ) T , cov ( w.^Y )

В соответствии с введенными ранее обозначениями Y = ln( S_ЗУ ) , Z = ln( S_ОКС ) , y = ln( s_ЗУ ) , z = ln( s_ЗУ ) .

Оценка РС как наиболее вероятное значение цены предложения V при заданных S_ЗУ = s_ЗУ, S_ОКС = s_ОКС (подробнее см. [2]) рассчитывается по следующей формуле:

Mode ( V|s _окс ,s _зу ) = exp { μ _W +^⎡_⎢⎣ COV ^- ¹ × cov

- σ _W ² +^⎡_⎢ COV ^- ¹ × cov

,cov

Оценка РС по условному математическому ожиданию:

E ( V|s окс ,s зу ) = exp { μ W +

COV ^- ¹ × cov ( X,Y ) , ( y

- μ _Y,z - μ _Z ) ^⎤_⎥+

1₂2 ^σW

^⎡ COV ^- ¹ × cov 2 ⎢⎣

,cov

Оценка РС по условной медиане рассчитывается по формуле:

^- T

Median ( V|s _0KC ,s _3y ) = exp U + I COV - 1 x cov ( X,Y ) , ( y - ц ^ /z - ^ _z ) l } . (14)

Поскольку в оценочной среде по-прежнему нет единого мнения относительно того, по какой числовой характеристике надо определять рыночную стоимость (по арифметическому среднему, среднему геометрическому или по оценке моды), может быть выбрана одна из формул (12), (13) или (14). В этом смысле подход к оценке единых объектов через изучение многомерного вектора ( V , S_ЗУ , S_ОКС ) дает более широкие возможности, чем формулы вида (9) и (10), дающие медианную оценку. В частности, если логарифмы компонент такого вектора распределены совместно нормально, то совместно нормально распределены и логарифмы компонент трехмерных векторов ( V / S_ОКС , S_ЗУ , S_ОКС ), ( V / S_ЗУ , S_ЗУ , S_ОКС ). По мнению автора, определению РС, данному в Федеральном законе от 29 июля 1998 года № 135-ФЗ «Об оценочной деятельности в Российской Федерации» (как и в USPAP, RICS, IVA), соответствует формула (12). Но кроме определения РС, есть более глубокое объяснение того факта, что в оценке следовало бы опираться на наиболее вероятные значения. Это особенно наглядно проявляется при рассмотрении многомерных распределений.

Рассмотрим пример, приведенный в работе [1].

Для логарифмов переменных «отношение цены к площади улучшений», «площадь зданий», «площадь земельного участка», указанных в таблице 2, получены следующие значения вектора средних, то есть μ _W = 10,2993, μ _Y = 8,4469, μ _Z = 9,3506, σ _W ² = 0,2381, σ _Y ² = 1,0635, σ _Z = 1,2140, ρ _WY σ _W σ _Y = ρ _YW σ _W σ _Y = 0,0108, ρ _WZ σ _W σ _Z = ρ _ZW σ _W σ _Z = 0,1467, ρ _YZ σ _Z σ _Y = ρ _YZ σ _Z σ _Y = 0,8978 и ковариационная матрица (см. табл. 6).

Таблица 6

Выборочные средние значения и ковариационная матрица для случайного вектора (W, Y, Z) *

Вектор средних
10,2993	8,4469	9,3506
Ковариационная матрица
0,2381	0,0108	0,1467
0,0108	1,0635	0,8978
0,1467	0,8978	1,2140

Таблица 7

Результаты оценки удельной РС, в рублях на 1 кв. м площади улучшений (ОКС) в зависимости от площадей ЗУ и ОКС

МОДАЛЬНЫЕ ЗНАЧЕНИЯ

		Плошадь земельного участка, кв. м
		2 000	7 000	12 000	17 000	22 000	27 000	32 000	37 000	42 000	47 000
>3 3 CD 9 м со л ^ СП 9 о 5	400	26 247	38 298	45 058	50 049	54 096	57 543	60 568	63 279	65 745	68 014
	2 400	16 938	24 714	29 076	32 297	34 909	37 133	39 085	40 835	42 426	43 890
	4 400	14 605	21 310	25 072	27 849	30 101	32 019	33 702	35 211	36 583	37 845
	6 400	13 327	19 445	22 877	25 411	27 466	29 216	30 752	32 129	33 381	34 533
	8 400	12 469	18 194	21 406	23 777	25 700	27 337	28 775	30 062	31 234	32 312
	10 400	11 835	17 269	20 317	22 567	24 392	25 947	27 311	28 533	29 645	30 668
	12 400	11 337	16 542	19 462	21 618	23 366	24 855	26 161	27 332	28 397	29 377
	14 400	10 930	15 948	18 763	20 842	22 527	23 962	25 222	26 351	27 378	28 323
	16 400	10 588	15 449	18 176	20 189	21 822	23 212	24 433	25 527	26 521	27 436
	18 400	10 294	15 021	17 672	19 629	21 217	22 569	23 755	24 818	25 786	26 675

МЕДИАНННЫЕ ЗНАЧЕНИЯ

		Плошадь земельного участка, кв. м
		2 000	7 000	12 000	17 000	22 000	27 000	32 000	37 000	42 000	47 000
>3 3 CD 9 м >* со 'О СП 9 о 5	400	31 947	46 615	54 843	60 918	65 844	70 039	73 722	77 021	80 023	82 784
	2 400	20 616	30 081	35 391	39 311	42 490	45 197	47 573	49 703	51 640	53 421
	4 400	17 777	25 938	30 517	33 897	36 638	38 972	41 021	42 858	44 528	46 064
	6 400	16 221	23 668	27 846	30 930	33 431	35 561	37 431	39 106	40 630	42 032
	8 400	15 177	22 146	26 055	28 941	31 281	33 274	35 023	36 591	38 017	39 329
	10 400	14 405	21 019	24 729	27 468	29 690	31 581	33 242	34 730	36 083	37 328
	12 400	13 799	20 134	23 688	26 312	28 440	30 252	31 843	33 268	34 564	35 757
	14 400	13 304	19 412	22 838	25 368	27 419	29 166	30 700	32 074	33 324	34 473
	16 400	12 887	18 804	22 123	24 574	26 561	28 253	29 739	31 070	32 281	33 395
	18 400	12 530	18 283	21 510	23 892	25 824	27 470	28 914	30 208	31 385	32 468

ЗНАЧЕНИЯ ПО МАТЕМАТИЧЕСКОМУ ОЖИДАНИЮ

		Плошадь земельного участка, кв. м
		2 000	7 000	12 000	17 000	22 000	27 000	32 000	37 000	42 000	47 000
>3 3 3 CD 9 м ^ со 'О СП 9 о 5	400	35 246	51 428	60 506	67 208	72 643	77 271	81 334	84 974	88 285	91 332
	2 400	22 744	33 187	39 045	43 370	46 877	49 864	52 485	54 835	56 971	58 937
	4 400	19 612	28 616	33 668	37 397	40 421	42 996	45 257	47 283	49 125	50 820
	6 400	17 895	26 112	30 721	34 124	36 883	39 233	41 296	43 144	44 825	46 372
	8 400	16 744	24 432	28 745	31 929	34 511	36 710	38 640	40 369	41 942	43 389
	10 400	15 893	23 189	27 283	30 305	32 755	34 842	36 674	38 315	39 809	41 182
	12 400	15 224	22 213	26 134	29 029	31 377	33 376	35 130	36 703	38 133	39 449
	14 400	14 677	21 416	25 196	27 987	30 250	32 178	33 869	35 385	36 764	38 033
	16 400	14 218	20 746	24 408	27 111	29 304	31 171	32 810	34 278	35 614	36 843
	18 400	13 824	20 170	23 731	26 359	28 491	30 306	31 899	33 327	34 626	35 821

О плотности застройки земельного участка

При заданном значении V = v по условному двумерному распределению случайных величин S_ЗУ , S_ОКС может быть оценена наиболее вероятная (средняя, средняя геометрическая) пара значений площади земельного участка и площади ОКС, соответствующая такой цене. При этом наиболее вероятная пара – единственна, а пары, которые соответствуют средним арифметическим и средним геометрическим значениям не единственны и обладают разными плотностями застройки при одной и той же фиксированной цене.

При заданных значениях V = v , S_ЗУ = s_ЗУ по одномерному условному распределению может быть оценено наиболее вероятное значение площади ОКС, соответствующее фиксированной цене и площади земельного участка.

Пусть V = v. Условное математическое ожидание:

E ( Y IW = w )

μ _Y + ρ _YW ( w - μ _W )

σ _W

μ Z + ρ ZW ^σZ ( w - μ W ) σ _W

Условная ковариационная матрица:

( ^

Y|W = w )

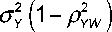
^σ Y ^σ Z ( ^ρ YZ ^- ^ρ YW ^ρ ZW )

⎜⎝ σ _Y σ _Z

( ^ρ YZ ^- ^ρ YW ^ρ ZW )

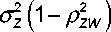
Наиболее вероятная пара s_ЗУ , s_ОКС , соответствующая фиксированному значению V = v :

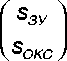
= mod e ( Y |V = v ) = exp [ E ( Y |

W = w ) - COV ( y IW = w ) • l ].

При фиксированном V = v положительная четверть плоскости S_ЗУ , S_ОКС является множеством точек, на котором определено двумерное распределение величин S_ЗУ , S_ОКС, логарифмы которых совместно нормальны с указанными параметрами. Точка максимума двумерной плотности – единственна, ее координаты дает формула (17). Пример такой плотности показан на рисунке 5 (см. с. 24). Для любой другой точки в плоскости S_ЗУ , S_ОКС существует множество других равновероятных точек, образующих линии, показанные на рисунке 6.

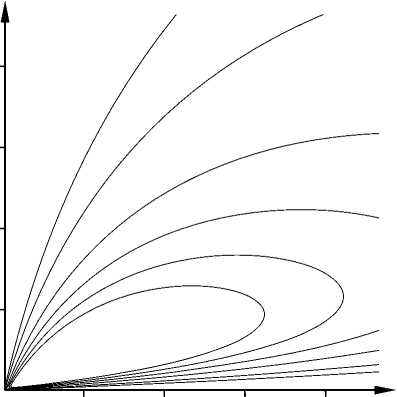
0 20 40 60 80

S _3y , тыс. KB. M

Рис. 6. Общий вид линий уровня равновероятных точек на плоскости с координатами S_ЗУ , S_ОКС

Формула (17) дает координаты точки максимума, которая хорошо видна на трех примерах, показанных на рисунке 5. Выбранная, в качестве оценки наиболее подходящей пары s_ЗУ , s_ОКС , любая другая точка положительной четверти плоскости S_ЗУ , S_ОКС попадает на линию уровня вида, показанного на рисунке 6.

Таким образом, если выбирается не точка максимума, то существует целое множество других, равновероятных точек. Плотность застройки участка в каждой такой точке будет разной (при одинаковом значении V = v).

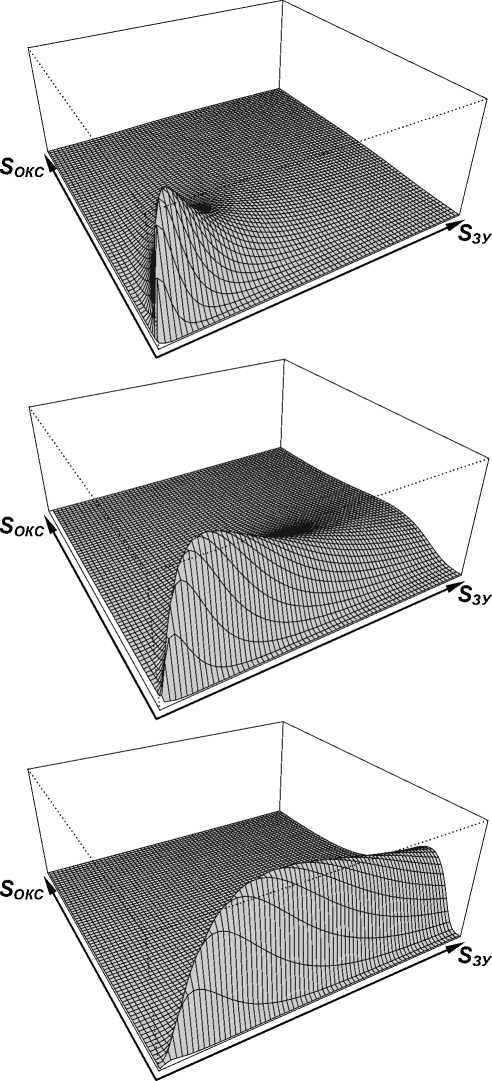
Рис. 5. Общий вид двумерной плотности распределения для случайных величин S_ЗУ , S_ОКС при различных фиксированных значениях V = v

Если зафиксировать, кроме V = v, площадь земельного участка S_ЗУ = s_ЗУ , то можно получить одномерный условный закон распределения (в данном случае логарифмически нормальный) для случайной величины S_ОКС. Для одномерной случайной величины, как уже неоднократно было показано (например, в работе [2]), оценки наиболее подходящего значения S_ОКС при заданных V = v, S_ЗУ = s_ЗУ могут быть сделаны по моде (наиболее вероятное значение единственное), по арифметическому среднему (оценка математического ожидания имеет еще одну равновероятную точку), среднему геометрическому (оценка медианы тоже имеет еще одну равновероятную точку). Делением результатов соответствующих оценок на площадь участка могут быть построены соответствующие зависимости для плотности застройки. Расчетные формулы для этого случая приведены в работе [1]. Здесь ограничимся только общим видом функциональных зависимостей s_ОКС от s_ЗУ и плотности застройки (коэффициента застройки) от s_ЗУ при фиксированном значении V = v .

Из рисунка 7 видно, что плотность (коэффициент) застройки нелинейно зависит от площади земельного участка при одном и том же значении V = v. Модель совместно нормального распределения логарифмов компонент вектора ( V , S_ЗУ , S_ОКС ) означает, что показанные на рисунке 7 функции являются степенны ́ ми. Линейную аппроксимацию таких зависимостей, как это видно из рисунка 7, следует применять осторожно, с выполнением двух условий:

• разброс значений площадей земельного участка объектов сравнения должен быть небольшим, позволяющим надеяться на относительно небольшую погрешность расчетов, в которых используется линейная зависимость вместо степенной;
• не допускается экстраполяция за пределы области наблюдаемых площадей объектов сравнения.

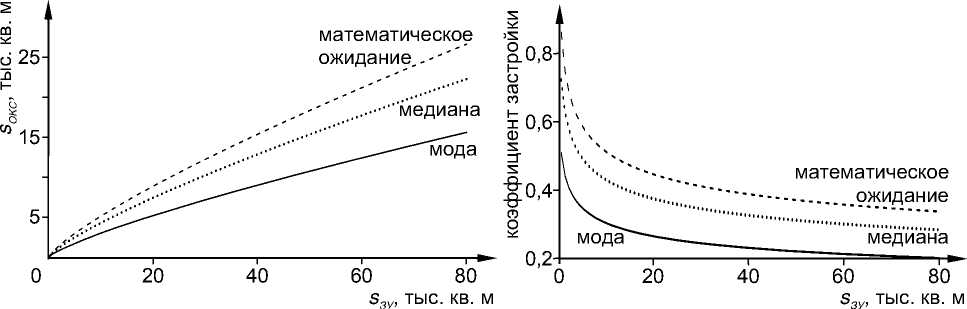
Рис. 7. Слева – зависимость s_ОКС от s_ЗУ при фиксированном значении V = v .

Справа – зависимость плотности (коэффициента) застройки z = S_ОКС / S_ЗУ от площади земельного участка s_ЗУ при фиксированном значении V = v

Заключение

Настоящая статья имеет практическую направленность. С теоретической точки зрения показанные в ней приемы являются известными, но до сих пор не освоенными в практике расчетов оценки РС объектов недвижимого имущества. Одним из возможных объяснений может служить традиционная приверженность оценщиков к Excel. Этот хорошо зарекомендовавший себя продукт является основным инструментом при подготовке отчетов об оценке. Использование специальных статистических пакетов не заменяет, а дополняет его, так как часть задач в специальных пакетах решается значительно быстрее. Другую часть задач, таких как модели множественной линейной регрессии, сводящиеся к ней модели, работа с индикативными переменными, проверка статистических гипотез и многое другое, лучше решать с использованием специальных пакетов, поскольку в Excel они могут быть решены с преодолением значительных трудностей либо вообще оказаться неразрешимыми.

Преимуществом модели множественной линейной регрессии, показанной в первой части статьи, являются:

• построение модели по всем предикторам одновременно;
• простая и наглядная интерпретируемость коэффициентов при индикативных переменных;
• возможность получать содержательные статистические характеристики получаемых моделей.

При этом труд оценщика становится более структурированным и включает следующие этапы:

• отбор и подготовка данных к применению специального пакета;
• обработка данных стандартными библиотечными функциями;
• интерпретация полученного результата.

Любой оппонент отчета об оценке в состоянии проделать такие же действия и получить такой же или близкий результат. Естественно, отбор объектов сравнения имеет первостепенное значение, особенно при работе с малыми выборками. Основной фокус работы оценщика смещается в область отбора, подготовки данных и интерпретации полученных результатов.

Использование модели, показанной во второй части статьи, в среде Excel трудоемко, занимает много времени. Такая модель вряд ли будет когда-либо использована оценщи- ком, работающим только в Excel. В среде специальных статистических пакетов однажды написанный программный код дает возможность применять его постоянно к разным данным и получать результаты гораздо быстрее, чем это происходит сейчас при подготовке расчетных частей отчетов об оценке. Более того, если подобным способом удается подобрать подходящую модель, то по этой модели могут быть получены результаты не только по конкретному объекту оценки, но и по всему множеству «сходных» объектов недвижимости, что позволяет с минимальными затратами времени рассчитывать таблицы. Особенностью подобных моделей является нелинейная зависимость исследуемых переменных (различных цен, стоимостей) от ценообразующих факторов (предикторов).

Список литературы Множественная линейная регрессия и многомерные модельные распределения при оценке единых объектов недвижимости

Ласкин М. Б. Многомерное логарифмически нормальное распределение в оценке недвижимого имущества // Бизнес-информатика. 2020. Т. 14. № 2. С. 48-63.
Ласкин М. Б. Логарифмически нормальное распределение цен и рыночная стоимость на рынке недвижимости // Известия Санкт-Петербургского государственного технологического института. 2014. № 25 (51). С. 102-106.
Об оценочной деятельности в Российской Федерации: Федеральный закон от 29 июля 1998 года № 135-ФЗ. Доступ из справочной правовой системы "КонсультантПлюс".

Статья научная