Множественная линейная регрессия и многомерные модельные распределения при оценке единых объектов недвижимости

#Просмотр данных

ТАВ

• #V-3a виси мая переменная

\/<-ТАВ$цена.в.млн.руб

Построение линейной модели по всем исходным предикторам

LMODEL<-lm(V~.,data=TAB)

summary(LMODEL)

Построение линейной модели

2<-ТАВ$площадь.ОКС.в.тыс.м/ГАВ$площадь.ЗУ.в.тыс.м.

#2-плотность застройки земельного участка z<-x1/x2

Нинейная модель по 3 предикторам с учетом взаимодействия одного из предикторов

• #с плотностью застройки

LMODEL<- т(1од(\/)~площадь.ЗУ+состояние.ОКС.хорошее+состояние.ОКС.удовлетворительное

+2:состояние.ОКС.удовлетворительное^аГа=ТАВ) summary(LMODEL)

Рис. 1. Код в статистическом пакете R для построения модели множественной линейной регрессии

Читатель самостоятельно может проверить качество моделей, получаемых для разных комбинаций предикторов и эффектов их взаимодействия, и выбрать лучшую. Для такой проверки не потребуется команд, отличных от показанных на рисунке 1. Но потребуется умение интерпретировать полученные результаты. В пакете R имеется обширная и хорошо подготовленная функция help(), которой вполне достаточно для того, чтобы за короткое время ознакомиться с функциями lm() и summary(). Среди всех рассмотренных моделей с точки зрения статистических характеристик для этого примера лучшей оказалась модель:

In V = 1,44 + 0,09 S_3y + 2,14 ОКС хор + 0,92 ОКС уд + 2,86 ОКС уд * z                       (5)

или

V = exp(1,44 + 0,09S3y + 2,14ОКСхор + 0,92ОКСуд + 2,86ОКСуд * z), где ОКСхор и ОКСуд – индикативные переменные, принимающие значения 1, если состояние ОКС хорошее или удовлетворительное.

На рисунке 2 показан результат работы функции lm() для такой модели.

Call:

lm(formula = log(V) ~ площадь.ЗУ + состояние.ОКС.хорошее + состояние. ОКС.удовлетворительное + 2:состояние.ОКС.удовлетворительное, data = TAB) Residuals:

1          2         3           4          5          6           7

6.731e-03 -3.289e-02 -5.855e-18 5.855e-18 2.616e-02 1.689e-02 -1.689e-02 Coefficients:

	Estimate	Std. Error	t value	Рг(>|Ф
(Intercept)	1.436178	0.045576	31.512	0.001006 **
площадь.ЗУ	0.089844	0.003696	24.310	0.001688 **
состояние.ОКС.хорошее	2.138417	0.031919	66.995	0.000223 ***
состояние.ОКС.удовлетворительное	0.916750	0.151001	6.071	0.026074 *
состояние.ОКС.удовлетворительное:2	2.861471	0.552862	5.176	0.035362 *

Signif. codes: 0 '***' 0.001 0.01 0.05 7 0.11' 1

Residual standard error: 0.03451 on 2 degrees of freedom Multiple R-squared: 0.9997, Adjusted R-squared: 0.999 F-statistic: 1457 on 4 and 2 DF, p-value: 0.0006861

Рис. 2. Результат работы функции lm() для линейной модели логарифма цены по предикторам: «площадь ЗУ», «состояние ОКС хорошее», «состояние ОКС удовлетворительное», с учетом эффекта взаимодействия предиктора «состояние ОКС удовлетворительное» и плотности застройки

Статистические показатели всех других моделей, которые можно было бы рассмотреть по имеющимся 7 объектам сравнения, хуже приведенных на рисунке 2.

Рассмотрим основные показатели качества модели.

Среднее ошибок равно 0,00000057, что несопоставимо меньше, чем размер исследуемых величин. На рисунке 3 показаны значения ошибок для каждого объекта сравнения.

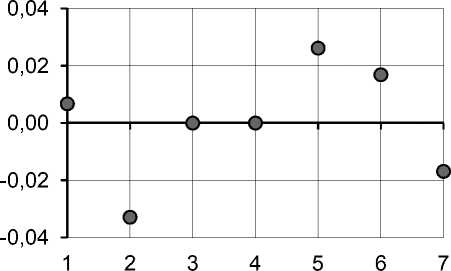
Рис. 3. Ошибки для объектов сравнения 1–7. По горизонтали – номер объекта сравнения в списке объектов сравнения из работы [4]. По вертикали – отклонение предсказанного по модели (5) значения от цены предложения с учетом скидки на торг (скидка на торг принята, как в работе [4])

Для исследования гомоскедастичности ошибок в этом примере недостаточно наблюдений, но значения ошибок достаточно низкие (максимальная ошибка 0,03289 – у второго объекта сравнения).

Оценки коэффициентов множественной регрессии проверяются с помощью критерия Стьюдента ( t -критерий). При применении библиотечной функции lm() нулевой гипотезой является: коэффициент незначимо отличается от нуля. Для того чтобы принять нулевую гипотезу, надо, чтобы p-value было как можно больше. В нашем случае p-value для всех коэффициентов меньше критического уровня 0,05, нет оснований принять нулевую гипотезу, она отвергается в пользу альтернативной: коэффициенты значимо отличаются от нуля.

RSE – стандартная ошибка всех отклонений, равна 0,03439.

Коэффициент детерминации R² = 0,9997, скорректированный R ² = 0,999.

Критерий Фишера и его p-value . При применении библиотечной функции lm() нулевой гипотезой является утверждение: линейная связь между зависимой и объясняющими переменными отсутствует. В нашем случае значение p-value низкое, нулевая гипотеза отвергается в пользу альтернативной: между зависимой и объясняющими переменными существует линейная связь.

Полученная модель хорошо описывает линейную связь между логарифмом цены и объясняющими переменными (предикторами).

В списке значимых факторов оказались:

• •    площадь земельного участка;

• •    индикативная переменная «ОКС находится в хорошем состоянии»;

• •    индикативная переменная «ОКС находится в удовлетворительном состоянии»;

• •    парная взаимосвязь плотности застройки участка и индикативной переменной «ОКС находится в удовлетворительном состоянии». Вошедшие в модель индикативные переменные никогда не равны 1 одновременно.

Интерпретация модели

Построенная модель означает следующее:

• 1)    если ОКС на участке нет, то ОКС_хор = 0 , ОКС_уд = 0, и модель принимает вид:

V = 4,20385 × exp(0,09 S_ЗУ );                                                            (6)

• 2)    если «ОКС находится в хорошем состоянии», то ОКС_хор = 1, ОКС_уд = 0, модель при-

• нимает вид:

V = 4,20385 x exp(0,09 S_3y + 2,139).                                                    (7)

В этом случае оценка РС зависит только от площади земельного участка, не зависит от площади ОКС и плотности застройки, за хорошее состояние ОКС принимается мультипликатор exp(2,139) = 8,49;

• 3)    если ОКС находится в удовлетворительном состоянии, то ОКС_хор = 0, ОКС_уд = 0 и модель принимает вид:

V = 4,20385 x exp(0,09 S_3y + 0,917 + 2,86 x S _okc / S_3y ).                                  (8)

В этом случае оценка РС зависит от площади земельного участка. За удовлетворительное состояние ОКС принимается мультипликатор exp(0,917) = 2,5. В ценообразовании участвует плотность застройки участка в виде мультипликатора exp(2,86 x s _okc / S_3y ).

Оценка РС объекта оценки

Для оценки РС объекта применяется выражение:

V = 4,20385 x exp(0,09 x 15,83 + 2,139) = 148,369 млн р.

Точность оценки, проведенной по имеющимся данным об объектах сравнения (интервал 2 σ ), составляет ±6,88 процента. Такая точность представляется достаточной с точки зрения оценки РС.

Интервальная оценка (для интервала ±2 σ ): РС объекта оценки находится в интервале [138,130; 158,507] (млн р).

Если на участке ОКС нет, то применяется формула (6). Удельная стоимость на единицу площади составит:

V I S_3y = [4,20385 x exp(0,09 S ЗУ )] / S_3y .

Отсюда видно, что удельная стоимость единицы площади зависит от того, на участке какой площади эта единица находится.

Выделенная оценка стоимости земельного участка для приведенного в примере объекта оценки составляет:

V = 4,20385 x exp(0,09 x 15,83) = 17,478 млн р.

Оценка удельной рыночной стоимости на единицу площади составит:

V / S_ЗУ = exp(0,09 S_ЗУ ) / S_ЗУ = 17,478 / 15,830 = 1,104 тыс. р. за 1 кв. м

Формулы (6), (7) и (8) имеют одинаковый сомножитель, относящийся к стоимости земельного участка: 4,20385 x exp(0,09 S_3y ), второй сомножитель в формуле (7) является константой exp(2,139) – мультипликатор, увеличивающий стоимость единого объекта за наличие на земельном участке ОКС, состояние которого признано хорошим, в формуле (8) второй сомножитель зависит от плотности застройки земельного участка exp(2,86 x S _okc I S_3y ).

При применении такой модели видно, что оценка РС единого объекта недвижимости не является простой арифметической суммой РС земельного участка и ОКС. В формулах участвуют экспоненты, зависящие от площадей ОКС и земельного участка. Если иметь в виду, что экспонента разлагается в ряд, где линейную часть представляют только два первых слагаемых, то можно увидеть, что применяя аддитивную модель по площадям ОКС и земельного участка можно потерять эффект остальных взаимодействий предикторов в оценке рыночной стоимости.

Необходимо прокомментировать полученные результаты:

• 1)    из формулы (7) следует, что при хорошем состоянии ОКС оценка РС вообще не зависит от площади объекта. Здесь следует отметить, что такой вывод сделан по модели (5), которая построена в условиях недостатка объектов сравнения для более подробного анализа. При таком количестве объектов сравнения и их характеристиках более точную модель получить невозможно. В то же время понятно, что зависимость от площади ОКС все-таки должна быть. Для ее выявления необходимо найти еще объекты сравнения. Модель, естественно, изменится, и могут быть сделаны более детальные выводы;

• 2)    сравнивая вторые сомножители в формулах (7) и (8), можно заметить, что из условия 2,139 = 0,917 + 2,86 x z ( z = S_OKC / S_3y ) следует, что при плотности застройки участка до 43 процентов единый объект с ОКС в хорошем состоянии будет дороже объекта с удовлетворительным состоянием ОКС, но при плотности застройки участка больше 43 процентов дороже окажется единый объект с ОКС, находящимся в удовлетворительном состоянии. Здесь тоже не помешал бы дополнительный анализ с привлечением большего количества аналогов, позволяющих учитывать большее количество предикторов и, что важно, эффектов их взаимодействия. В целом, представляется, что в этих на первый взгляд странных для оценщика особенностях проявляется эффект синергии единого объекта недвижимости, который дает основания сомневаться в том, что РС единого объекта является арифметической суммой РС ОКС и РС земельного участка.

Исходя из изложенного представляется обоснованным отдельное изучение связи между ценой единого объекта недвижимости и площадей земельного участка и ОКС как функции двух переменных. Такое изучение, по-видимому, можно было бы провести после корректировок объектов сравнения по модели множественной линейной регрессии по ранговым предикторам. В приведенном примере для такого подхода недостаточно объектов сравнения. В то же время метод одновременных корректировок по ансамблю ранговых предикторов требует дополнительного изучения, и пока ограничимся рассмотрением примера, в котором такая корректировка не требуется.

Пример 2

Данные для примера 2 опубликованы А.А. Слуцким и И.А. Слуцкой (см. [2]). Прежде чем переходить к примеру, следует отметить, что существуют несколько способов корректировок на различие объекта оценки от объектов сравнения по фактору «площадь». Обзор таких способов можно посмотреть в работе [14]. При внимательном рассмотрении все они сводятся к одному и тому же принципу: зависимость цены объекта (предложения/сделки) от площади ОКС или от площади земельного участка имеет характер степенной функции. Пусть V = A х S pKC - предполагаемая зависимость РС от площади ОКС, V = B х S jy - предполагаемая зависимость РС от площади земельного участка. Следствием такого вида зависимости является известная формула корректировки (как для площади ОКС, так и для площади земельного участка):

V KOP = V O6CP. ^{Х (} ^б.оц. / S 06cp)p и

Vkop    Vo6cp. Х (Sоб.оц. / So6.ср.)q, где Vкор – скорректированная цена;

• V_об.ср. – цена объекта сравнения;

• S_об.оц. – площадь (ОКС или ЗУ) объекта оценки;

• S_об.ср. – площадь (ОКС или ЗУ) объекта сравнения;

• p – коэффициент торможения (эффекта масштаба) по площади ОКС;

• q – коэффициент торможения (эффекта масштаба) по площади ЗУ.

В статье [16] приведено теоретические обоснования такой зависимости как результата часто получающей подтверждение гипотезы о совместном логарифмически нормальном распределении цен и площадей с отрицательным коэффициентом корреляции. Особенностью оценки РС единых комплексов является то, что цена и оценка РС при прочих равных условиях являются функцией двух переменных V = f ( S_ОКС , S_ЗУ ) и существуют достаточные основания предполагать, что такая функция будет нелинейной.

Один из возможных вариантов одновременного учета S_ЗУ и S_ОКС – рассмотреть модель множественной линейной регрессии вида ( C , p , q – параметры):

ln y = ln C + q ln S_ЗУ + p ln S_ОКС + ɛ ;

ln V = E (ln y ) = ln C + q ln S_ЗУ + p ln S_ОКС .

При потенцировании эта модель даст медианную оценку зависимости РС вида:

V = C x S q x S^_c .

Такая модель не дает возможности учета земельных участков с S_ОКС = 0, исходя из этого единый объект недвижимости и свободный земельный участок являются разными классами объектов недвижимого имущества и не могут быть использованы вместе при оценке единых объектов.

Другой возможный вариант одновременного учета S_ЗУ и S_ОКС – изучение эмпирического распределения трехмерного случайного вектора ( y , S_ЗУ , S_ОКС ) , подбор подходящего (если удается) модельного

Таблица 2

Данные о 40 единых объектах недвижимости производственноскладского назначения

§ о C to	1 s	to о	hl^
400	2 500	20,5	51 250
750	5 000	18	24 000
1 081	3 378	26	24 052
1 130	6 638	27,5	24 336
1 320	4 167	31,5	23 864
1 440	10 000	160	111 111
1 790	3 462	93	51 955
1 900	13 000	85	44 737
2 125	5 623	85	40 000
2 642	5 183	75	28 388
2 700	6 800	59	21 852
1 820	2 737	32	17 582
2 250	9 252	84	37 333
2 973	5 388	90	30 272
3 513	10 000	80	22 773
3 600	5 000	95	26 389
4 000	13 558	140	35 000
4 124	12 866	91	22 066
4 167	5 000	125	29 998
4 257	6 861	128,5	30 186
5 292	11 143	56	10 582
5 300	16 000	220	41 509
6 011	11 319	135	22 459
6 013	20 781	90	14 968
6 060	21 790	179	29 538
6 123	2 390	152,49	24 904
6 479	7 337	119	18 367
6 756	4 220	90	13 321
10 000	12 000	420	42 000
10 300	17 000	312	30 291
10 672	12 194	350	32 796
10 990	30 000	480	43 676
12 000	30 000	300	25 000
13 000	55 000	200	15 385
14 428	33 000	385	26 684
15 000	37 000	840	56 000
18 924	20 600	800	42 274
22 312	40 162	338,54	15 173
34 082	478 000	2 500	73 353
35 000	160 000	2 400	68 571

распределения ( V , S_ЗУ , S_ОКС ) , построение необходимых оценок по модельному распределению.

В работе [2] приведены данные о 40 объектах недвижимости производственно-складского назначения в городе Санкт-Петербурге, выставлявшихся на продажу осенью 2019 года. Следуя авторам работы [2], отказавшимся от корректировок объектов сравнения по всем факторам, кроме площадей ОКС и земельного участка, будем считать, что корректировки не требуются. Данные представлены в таблице 2.

Будем искать модель множественной линейной регрессии в виде уравнения (9). На рисунке 4 представлен результат работы функции lm() для такой модели:

Call:

lm(formula = Iog(y2) ~ Iog(x1) + Iog(x2), data = TAB) Residuals:

Min 1Q Median 3Q Max

-0.9917 -0.2847 0.0733    0.2893 1.0742

Coefficients:

	Estimate	Std. Error	t value	Pr(>|t|)
(Intercept)	2.6364	0.6472	4.073	0.000235 ***
Ipg(x1)	0.7555	0.1153	6.553	1.12e-07 *“
Iog(x2)	0.3016	0.1079	2.795	0.008182 **

Signif. codes: 0 '***' 0.001    0.01   0.05 7 0.1 " 1

Residual standard error: 0.4551 on 37 degrees of freedom

Multiple R-squared: 0.8515, Adjusted R-squared: 0.8434

F-statistic: 106.1 on 2 and 37 DF,........p-value: 4.768e-16

Рис. 4. Результат работы функции lm() для модели (9)

Окончание в следующем номере журнала.