Множественное встраивание водяных знаков в пространственно-частотную область изображений на основе генетического алгоритма

В современном мире роль различного цифрового контента, в том числе цифровых изображений, в жизни людей становится всё более значимой. Каждый день пользователи интернета и социальных сетей обмениваются огромным количеством фотографий и различных иллюстраций. Однако широкое использование цифрового контента связано с рядом проблем кибербезопасности. Одной из таких проблем является проблема определения авторства фотографии или иллюстрации, опубликованной в сети. Возможности социальных сетей позволяют создателям контента удобно делиться результатами своей творческой деятельности с огромным количеством людей, однако одновременно они дают злоумышленнику шанс создать копию некоторого цифрового объекта и далее распространять его под своим именем, в том числе с коммерческими целями. В этом случае автору оригинального изображения может быть очень сложно защитить свои права. Эффективным решением данной проблемы является применение технологии цифровых водяных знаков (ЦВЗ).

ЦВЗ представляет собой дополнительную информацию, позволяющую идентифицировать автора или обладателя цифрового контента, в частности, цифрового изображения. На практике в качестве такой информации часто используется логотип, однако в общем случае водяной знак может представлять собой текстовые данные или случайную битовую комбинацию, содержащую в себе некоторый цифровой идентификатор. Водяной знак в виде логотипа может быть добавлен на изображение видимым образом, чтобы осложнить неправомерное использование и распространение цифрового изображения злоумышленником. Такой подход обычно используется в тех ситуациях, когда автор не заинтересован в демонстрации оригинального изображения зрителю, например, до внесения оплаты. Однако в том случае, если автор изображения использует его для иллюстрации новостей или в рекламных целях, видимый водяной знак нарушает восприятие контента зрителем, что противоречит цели привлечения внимания к данному контенту. В таком случае лучшим решением является добавление водяного знака незаметным образом, чтобы сам факт его наличия был тайной для зрителя. Та- кие водяные знаки называются невидимыми, а факт добавления водяного знака к цифровому объекту называется встраиванием. Данное исследование посвящено невидимому встраиванию водяных знаков.

Общая схема использования невидимых ЦВЗ выглядит следующим образом. На этапе встраивания автор или обладатель цифрового изображения незаметным образом добавляет к нему ЦВЗ. Результатом встраивания является цифровое изображение, содержащее водяной знак, но визуально неотличимое от исходного. Если такое изображение размещается в открытом доступе в сети, злоумышленник может его скопировать и попытаться присвоить авторство. В случае возникновения спора об авторстве оригинального изображения автор или владелец может применить соответствующий алгоритм извлечения и извлечь ЦВЗ из незаконной копии, тем самым подтвердив её принадлежность. Однако на практике злоумышленник может подвергнуть созданную им копию изображения различным искажениям, которые в контексте ЦВЗ называются атаками. Полный перечень возможных атак на ЦВЗ является достаточно обширным, однако чаще всего атакующие используют основные операции обработки изображений, такие как изменение яркости и контрастности, усиление резкости и другие. В результате применения некоторой атаки изображение, содержащее ЦВЗ, оказывается искажено. Чтобы обеспечить надёжное доказательство авторства контента или владения им, водяной знак должен быть извлечён из искажённого изображения с определённым уровнем качества. В этом случае можно говорить о робастности схемы ЦВЗ.

В этом исследовании предлагается новый алгоритм робастного встраивания ЦВЗ в цифровые изображения. Его отличительные особенности заключаются в следующем:

• •    встраивание ЦВЗ выполняется в гибридную пространственно-частотную область цифровых изображений;

• •    робастность встраивания достигается за счёт множественного встраивания копий оригинального ЦВЗ;

• •    для обеспечения высокого уровня незаметности используется генетический алгоритм (ГА), который находит близкую к оптимальной матрицу изменений в пространственной области для каждого блока изображения;

• •    для извлечения ЦВЗ не требуется оригинальное изображение или оригинальный ЦВЗ.

1.    Обзор литературы

Методы ЦВЗ позволяют решать разные задачи, связанные с защитой цифрового контента, такие как защита авторских прав, контроль копирования, аутентификация контента [1]. Различные схемы встраивания ЦВЗ отличаются по уровню незаметности наличия водяного знака в цифровом объекте и уровню робастности, т.е. устойчивости к различным искажениям. Для решения многих задач в области защиты изображений наилучшим образом подходят невидимые робастные ЦВЗ, которые не мешают восприятию контента зрителем, но могут быть обнаружены в изображении даже после определённой постобработки. Защищённость встраивания от типичных атак, таких как изменение яркости или кадрирование, является приоритетом для многих разработчиков схем ЦВЗ, поскольку такие атаки могут носить как преднамеренный, так и непреднамеренный характер и быть совершены законным владельцем копии изображения по ошибке или по незнанию [2].

С точки зрения извлечения ЦВЗ выделяют слепые [3, 4] и не слепые [5, 6] схемы. Слепые схемы не требуют предъявления оригинального изображения или водяного знака при извлечении, в то время как не слепые схемы используют некоторые оригинальные данные на этапе извлечения ЦВЗ. На практике слепые схемы более удобны и подходят для решения широкого круга задач, поэтому многие исследователи стремятся к достижению слепого извлечения в своих алгоритмах ЦВЗ.

По способу организации пространства сокрытия данных схемы ЦВЗ делятся на схемы встраивания в пространственной области и в области преобразований. Пространственное встраивание работает напрямую со значениями пикселей изображений [7, 8]. Встраивание в область преобразований предполагает некоторое преобразование матрицы пикселей перед встраиванием и внесение изменений в элементы данных, полученные после такого преобразования. Наибольшую часть методов встраивания в области преобразований составляют методы встраивания в частотную область изображений, работающие с коэффициентами различных частотных преобразований, таких как дискретное косинусное преобразований (ДКП), дискретное преобразование Фурье (ДПФ), дискретное вейвлет-преобразование (ДВП) [9, 10]. Преимуществом пространственного встраивания является высокая незаметность и более низкая вычислительная сложность, однако робастность такого встраивания обычно ниже, чем у встраивания в область преобразований, в частности, частотную область. Поэтому среди схем встраивания ЦВЗ преобладают схемы частотного встраивания. К методам, работающим в области преобразования, относятся также методы, работающие, например, с разложением матрицы по сингулярным значениям или QR-разложением [11].

Существуют различные подходы к повышению эффективности встраивания ЦВЗ. Для достижения компромисса между незаметностью и робастностью многие авторы используют метаэвристическую оптимизацию. Метаэвристики позволяют эффективно исследовать пространство поиска даже в трудно формализуемых задачах и хорошо подходят для сферы встраивания ЦВЗ. В современных работах встречаются как классические метаэвристики, так и новые, предложенные в последние годы. Например, в схеме пространственного встраивания [12] популярный алгоритм оптимизации роя частиц направлен на поиск оптимального коэффициента масштабирования, балансирующего незаметность и робастность. В работе [13], посвящённой частотному встраиванию, аналогичная задача решается с помощью ГА. В то же время, например, авторы [14] и [15] используют соответственно алгоритмы оптимизации на основе преподавания-обучения (TLBO) и оптимизации муравьиного льва, достаточно новые и пока не нашедшие широкого применения в области встраивания дополнительной информации в изображения.

Другим распространённым подходом, направленным непосредственно на повышение робастности, является повышение избыточности встраивания. Например, в работе [11] предлагается встраивать по 4 копии битов водяного знака для борьбы с атаками кадрирования. Наряду со множественным встраиванием, используется дополнительный ЦВЗ для обнаружения искажённых копий робастного водяного знака. В работе [16], направленной на обеспечение устойчивости к съёмке с экрана, водяной знак неоднократно встраивается в разные области изображения для повышения надежности.

Таким образом, существует ряд критериев эффективности алгоритмов встраивания ЦВЗ и путей достижения высоких показателей по этим критериям, каждый из которых выбирает приоритетом разные показатели. В данном исследовании предлагается алгоритм, который объединяет пространственное и частотное встраивание, метаэвристическую оптимизацию и множественное встраивание для достижения высокой незаметности, робастности и возможности слепого извлечения.

2.    Предлагаемый подход

В этом параграфе представлены основные идеи данного исследования. В частности, рассматриваются особенности организации множественного встраивания ЦВЗ в пространственно-частотную область цифровых изображений с помощью матрицы изменений и поиска такой матрицы с использованием метаэври-стической оптимизации.

• 2.1.    Множественное встраивание водяных знаков в пространственно-частотную область изображений

Ранее в работе [17] был предложен новый подход ко встраиванию информации в гибридную пространственно-частотную область цифровых изображений. Описанный в [17] подход сочетает встраивание данных в пространственную область изображений с извлечением встроенных данных из элементов частотной области. Обработка изображения начинается с разбиения на неперекрывающиеся блоки раз- мером 8×8 пикселей. Встраивание очередного фрагмента информации в каждый блок выполняется путём сложения значений пикселей блока с элементами матрицы изменений, представляющей собой матрицу того же размера, что и блок изображения, и заполненную целыми числами из отрезка [– k; k]. Для извлечения информации к блокам изображения применяется двумерное ДКП, и фрагмент сообщения извлекается по формуле (1), использующейся в классическом методе модуляции индекса квантования (QIM) [18– 20].

b = arg min | C ( x , y ) - C p ( x , y )|,                   (1)

P e [ 0.1 ]

где C ( x , y ) – это коэффициент ДКП, содержащий встроенный бит ЦВЗ b ,

[ C ⁽ x , У

C 0 ( x, y ) = Sign C ( x, y ) ■ q---------¹

q

( C ( x , y )l q

Ci (x,y) = sign C(x,y)■ q'-------— + y , q 2

q – это шаг квантования.

Стоит отметить, что в общем случае 1 <  x, y <  8, однако для извлечения используются только некоторые среднечастотные коэффициенты, конкретные позиции определяются параметрами алгоритма.

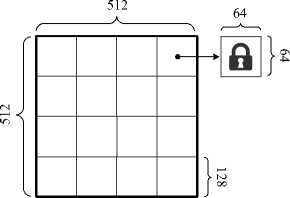
В работе [17] данный подход позволял осуществлять стеганографическое встраивание, т.е. решать задачу передачи большого объёма информации незаметным для третьих лиц образом. Отличительной особенностью предложенного ранее алгоритма являлось безошибочное извлечение встроенной информации в отсутствие каких-либо искажающих воздействий на изображение с вложением, однако устойчивость к атакам не рассматривалась. В этом исследовании предлагается расширить подход ко встраиванию в пространственно-частотную область изображений для встраивания невидимых робастных ЦВЗ. Чтобы обеспечить более высокую робастность, используется увеличение избыточности информации путём реализации множественного встраивания, согласно которому в изображение встраивается несколько копий водяного знака. Количество таких копий зависит от размеров исходного изображения и водяного знака, а также от количества среднечастотных коэффициентов ДКП, использующихся для извлечения информации. Например, в изображении размером 512×512 пикселей можно скрыть 16 копий двоичного изображения водяного знака размером 64×64 при использовании 16 коэффициентов ДКП, при этом каждая копия будет занимать квадрат размером 128×128 пикселей. Примеры расположения ЦВЗ в оригинальном изображении и фрагмента ЦВЗ в блоке изображения показаны на рис. 1 а , б .

На этапе извлечения копии ЦВЗ извлекаются отдельно, и значение каждого отдельного бита определяется путём вычисления средних значений битов копий ЦВЗ на соответствующих позициях и округления. Такой подход позволяет существенно повысить робастность встраивания, поскольку искажения одной или нескольких копий водяного знака могут быть компенсированы за счёт других копий, претерпевших меньшие искажения либо вовсе не подвергавшихся искажениям, например, при наложении шума или добавлении новых объектов на изображение.

а)                           ¹²⁸

DC	1	5	6	14	15	27	28
2	4	7	13	16	26	29	42
3	8	12	17	25	30	41	43
9	11	18	24	31	40	44	53
10	19	23	32	39	45	52	54
20	22	33	38	46	51	55	60
21	34	37	47	50	56	59	61
35	36	48	49	57	58	62	63

Рис. 1. Пример расположения: (а) копий ЦВЗ в изображении, (б) фрагмента ЦВЗ в блоке ДКП

• 2.2.    Генетический алгоритм

Выбор подходящей матрицы изменений оказывает существенное влияние на визуальное качество изображений, содержащих водяные знаки, а также на их устойчивость к различным операциям постобработки. Незаметность встраивания в подавляющем большинстве исследований, посвящённых встраиванию информации в цифровые изображения, оценивается путём вычисления значения метрики пиковое отношение сигнала к шуму (PSNR). Чем выше значение PSNR, тем выше степень сходства двух изображений. Значение PSNR рассчитывается следующим образом:

PSNR = 20 ■ log₁₀

MAX

MSE ^,

MN

MSE  ш Ш OI (x, y)-WI (x, y ))2, x —1 y—1

где M и N – это высота и ширина изображения, OI(x, y) – это пиксель оригинального изображения, WI(x, y) – это пиксель изображения со встроенным водяным знаком, MAX – это максимальное значение, принимаемое пикселем изображения, т.е. 255.

Одной из наиболее распространённых метрик робастности встраивания является коэффициент битовых ошибок (BER), показывающий отношение количества инвертированных при извлечении битов к общему количеству встроенных битов. Увеличение данного значения свидетельствует об увеличении числа ошибок. Значение BER вычисляется следующим образом:

BER —

Z ",X n—1 \OW (', J)-EW (i, j )l mn

,

где m и n – это высота и ширина водяного знака, OW ( i , j ) – это пиксель оригинального водяного знака, EW ( i , j ) – это пиксель извлечённого водяного знака.

Подходящая матрица изменений может быть найдена путём полного перебора вариантов. Полный перебор требует сложения значений пикселей блока с элементами каждой возможной матрицы изменений, вычисления соответствующих значений метрики PSNR, выполнения ДКП и расчёта соответствующих значений BER при извлечении. Данная последовательность действий, которую будем называть циклом встраивания, должна быть выполнена для каждого блока изображения. Тогда количество циклов встраивания, требуемое для полного перебора вариантов, описывается выражением (7).

O e — ( 2 k + 1 ) 64

MN

X .

В случае полного перебора вариантов необходимо около 1,72×10⁸⁸ циклов встраивания для изображения размером 512×512 и k = 10.

Проблема обеспечения баланса между незаметностью и робастностью может рассматриваться как проблема оптимизации. В рамках данного исследования предлагается использовать метаэвристическую оптимизацию для поиска подходящего решения. Ме-таэвристическая оптимизация не гарантирует нахождение оптимального решения, однако близкое к оптимальному решение, найденное с помощью метаэвристики, обеспечивает разумный компромисс между вычислительными затратами и эффективностью.

Существует большое количество разных метаэвристик [21]. Для задач, в которых искомое решение представляет собой набор целочисленных значений, хорошо подходит классический ГА [22], имитирующий эволюционные процессы. ГА-поиск выполняется в течение определённого количества итераций G, которые называются поколениями. Множество решений задачи называется популяцией, и каждое решение задачи соответствует одной из P особей популяции. Качество решения, соответствующего особи, оценивается с помощью специальной функции приспособленности. В каждом новом поколении особи с луч- шим значением функции приспособленности полу- чают преимущество и постепенно «вытесняют» менее приспособленные особи. Для получения новых особей выполняются операторы кроссовера и мутации.

В данном исследовании каждая особь популяции соответствует возможному варианту матрицы изменений с целыми значениями из промежутка [– k; k]. Для ускорения сходимости при формировании начальной популяции, помимо случайных значений, используются значения, соответствующие изменениям блока пикселей после пробного встраивания информации в коэффициенты ДКП [17]. Размер особи соответствует размеру блока пикселей изображения и равен 64. В процессе работы ГА реализуется одноточечный кроссовер, который выбирает двух случайных особей из популяции с вероятностью pcr и создаёт двух потомков путём объединения их фрагментов в случайно выбранной точке, как показано на рис. 2. Каждый из потомков мутирует с вероятностью pmut, в результате чего случайно выбранный элемент особи принимает случайное целое значение из промежутка [– k; k], как показано на рис. 2.

P -1

P

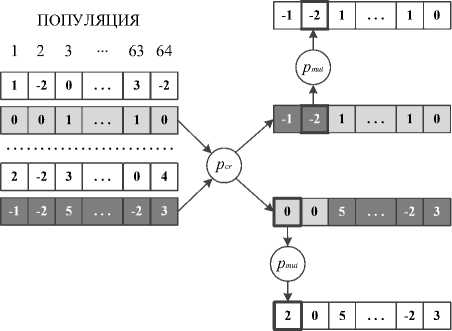
Рис. 2. Операторы ГА: кроссовер и мутация

Функция приспособленности сочетает метрики незаметности и робастности, в частности, PSNR и BER, и её значение максимизируется в процессе оптимизации. Величина BER принадлежит промежутку [0; 1], в то время как значение PSNR составляет около 30–50 дБ для разных блоков. В процессе поиска лучшего решения приоритет отдаётся робастности, поэтому итоговый вид функции приспособленности задаётся следующим выражением:

F = 10 - 4 PSNR + ( 1 - BER ) . (8)

При использовании ГА количество циклов встраивания, необходимых для выбора матрицы изменений, можно оценить следующим образом

OGA

MN

----X

( P + GP ) .

В данном случае количество циклов встраивания напрямую зависит от значений параметров ГА, таких как число поколений G и размер популяции P. Например, при G = 100 и P = 100 потребуется около 4,14×107 циклов встраивания для изображения размером 512×512. Таким образом, использование метаэв-ристической оптимизации существенно снижает вычислительную сложность алгоритма.

Для оценки влияния замены частотной области ДКП для встраивания на гибридную пространственно-частотную область необходимо отдельно учитывать операции ДКП и обратного ДКП при реализации циклов встраивания. Внесение изменений в коэффициенты ДКП при встраивании требует выполнения обратного ДКП для формирования блока пикселей изображения с ЦВЗ на этапе вычисления целевой функции и прямого ДКП для извлечения встроенных данных и вычисления метрики BER, следовательно, общее число частотных преобразований в 2 раза превышает число циклов встраивания, рассчитанное по формуле (9). Предложенная схема встраивания в гибридную пространственно-частотную область осуществляет только прямое ДКП при каждом вычислении целевой функции, следовательно, оценка числа частотных преобразований совпадает с оценкой числа циклов встраивания по формуле (9).

• 2.3.    Алгоритмы встраивания и извлечения

Сформулируем алгоритм встраивания.

Вход: оригинальное изображение OI размером M × N , двоичное изображение водяного знака OW размером m × n , значение шага квантования q , количество ДКП-коэффициентов для извлечения данных D , интервал допустимых значений [– k ; k ], размер популяции P число поколений G , вероятность кроссовера p cr , вероятность мутации p mut .

Выход: изображение с водяным знаком WI .

Шаг 1. Открыть входное изображение OI и разде лить его на равные квадраты со стороной 8 mn D . Пиксели за пределами полученных квадратов не участвуют в процессе встраивания. Для наилучшей производительности алгоритма значения m, n и D стоит выбирать таким образом, чтобы каждый блок изображения содержал фрагмент ЦВЗ.

Шаг 2. В каждый из полученных квадратов встроить одну копию водяного знака OW . Для этого выполнить следующее:

Шаг 2.1. Преобразовать изображение водяного знака в битовую последовательность и разделить её на фрагменты по D битов.

Шаг 2.2. Разделить текущий квадрат изображения на блоки размером 8×8 пикселей.

Шаг 2.3. Для каждого блока выполнить:

Шаг 2.3.1. Сгенерировать начальную популяцию из P особей – вариантов матрицы изменений.

Шаг 2.3.2. Оценить значение функции приспособленности для каждой особи по формуле (8).

Шаг 2.3.3. Найти лучшую матрицу изменений с помощью ГА в течение G поколений.

Шаг 2.3.4. Выполнить встраивание фрагмента ЦВЗ в оригинальные значения пикселей текущего блока с помощью найденной матрицы изменений.

Шаг 3. Сформировать изображение с водяным знаком WI и завершить алгоритм.

Далее сформулируем алгоритм извлечения. Стоит отметить, что предложенный алгоритм извлечения является слепым. Это значит, что для извлечения не требуется ни оригинального изображе- ния, ни оригинального водяного знака. Параметры, используемые при извлечении, могут рассматриваться в качестве секретного ключа и использоваться для разных защищаемых изображений и разных водяных знаков.

Вход: изображение с ЦВЗ WI размером M × N , размеры ЦВЗ m × n , значение шага квантования q , количество ДКП-коэффициентов для извлечения D .

Выход: извлечённый водяной знак EW .

Табл. 1. Значения метрик PSNR и BER для отдельных изображений и атак

Изображение	1	2	3	4	5	6	7	8
PSNR, дБ	42,2471	40,6786	42,0585	42,3368	41,9352	42,5992	42,6933	40,9250
Атака	BER
Нет	0	0	0	0	0	0	0	0
Контраст +10	0	0,0628	0,0008	0,0039	0,0018	0	0	0,0294
Контраст –10	0,0625	0,0205	0,0492	0,0401	0,0262	0,0665	0,0388	0,0171
Выравнивание гистограммы	0,1613	0,2979	0,0104	0,2466	0,0962	0,0081	0,0167	0,1361
Усиление резкости	0,0034	0,1900	0,0203	0,0609	0,0651	0,0020	0,0144	0,1598
Шум «соль-перец»	0,0223	0,0253	0,0198	0,0213	0,0207	0,0282	0,0228	0,0222
Яркость +10	0	0	0	0	0	0	0	0
Яркость –10	0	0	0	0	0	0	0	0
Добавление объекта	0	0	0	0	0	0	0	0
Кадрирование (угол)	0	0	0	0	0	0	0	0
Кадрирование (центр)	0	0	0	0	0	0	0	0
Среднее	0,0227	0,0542	0,0091	0,0339	0,0191	0,0095	0,0084	0,0331

Шаг 1. Открыть входное изображение WI и разде лить его на равные квадраты со стороной 8 л/ mn/D . Пиксели за пределами полученных квадратов не участвуют в процессе извлечения.

Шаг 2. Из каждого из квадратов извлечь одну копию ЦВЗ. Для этого выполнить следующее:

Шаг 2.1. Разделить текущий квадрат изображения на блоки размером 8×8 пикселей.

Шаг 2.2. Для каждого блока:

Шаг 2.2.1. Выполнить ДКП.

Шаг 2.2.2. Извлечь фрагмент водяного знака из D среднечастотных коэффициентов по формуле (1).

Шаг 2.3. Сформировать текущую копию водяного знака из извлечённых фрагментов.

Шаг 3. Сложить поэлементно биты всех полученных копий водяного знака, вычислить соответствующие средние значения и округлить до целых.

Шаг 4. Сформировать извлечённый водяной знак EW и завершить алгоритм.

3.    Результаты экспериментов

В этом параграфе представлены результаты вычислительных экспериментов с предложенным алгоритмом. Для экспериментов использовались 8 стандартных изображений в градациях серого из базы USC-SIPI [23] размером 512×512. В качестве водяного знака использовалось двоичное изображение размером 64×64, следовательно, ёмкость встраивания составила 4096 бит. Эксперименты проводились на компьютере с процессором Intel i5 с тактовой часто- той 2,9 ГГц и 16 ГБ ОЗУ (ОС Windows 10). Программа написана на языке программирования C++.

Параметры алгоритма следующие: значение шага квантования q = 16, количество ДКП-коэффициентов для извлечения D = 16, параметр интервала допустимых значений k = 10. Параметры ГА: вероятность мутации p mut = 0,2, вероятность кроссовера p cr = 0,6, размер популяции P = 100, размер каждой особи равен 64, количество поколений G =30. Эксперименты повторялись 10 раз для каждого изображения.

Для оценки робастности был реализован следующий набор атак: нет атаки; увеличение контрастности на 10; уменьшение контрастности на 10; выравнивание гистограммы; усиление резкости; добавление шума «соль-перец» с плотностью 0,01; увеличение яркости на 10; уменьшение яркости на 10; добавление объекта (белый квадрат 160×160) на изображение; кадрирование от угла до размера 256×256; кадрирование по центру до размера 256×256.

Рис. 3 демонстрирует влияние количества поколений ГА G на средние значения метрик незаметности PSNR (4) и робастности BER (6) для восьми изображений. Как следует из графика, представленного на рис. 3, увеличение числа поколений улучшает незаметность встраивания (увеличивает значение PSNR) и ухудшает устойчивость к отмеченному выше перечню атак (увеличивает значение BER).

Табл. 1 демонстрирует значения незаметности встраивания для 8 изображений, а также значения метрики робастности BER для разных атак.

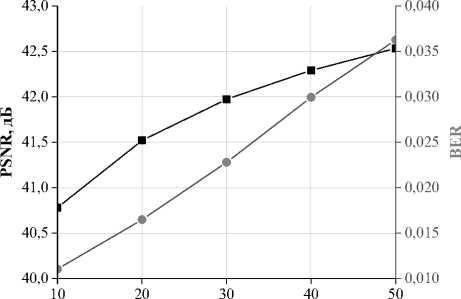
Количество поколений G

Рис. 3. Зависимость значений PSNR и BER от количества поколений ГА

Дополнительно для оценки робастности было оценено значение нормализованного коэффициента взаимной корреляции (NCC) между исходным и извлечённым ЦВЗ, близкое к 1 значение которого говорит о высокой степени сходства изображений. Значение NCC вычисляется следующим образом:

-—JmjWij^

■^j Wj) ^ij Wj' )

Значения метрики NCC представлены в табл. 2.

На рис. 4 представлены примеры фрагментов изображения 1 из табл. 1 и 2 («Airplane») до и после встраивания ЦВЗ. Рис. 5 показывает пример атаки на изображение с водяным знаком и извлечённый водяной знак. Табл. 3 показывает средние значения метрик BER и NCC для 8 изображений по каждой атаке.

Рис. 4. Примеры: а) фрагмент изображения до встраивания ЦВЗ; б) оригинальный ЦВЗ; в) фрагмент изображения после встраивания ЦВЗ

Результаты экспериментов демонстрируют высокую эффективность предложенного алгоритма. PSNR во всех случаях превышает 40 дБ, в то время как значение 30–35 дБ считается пороговой величиной незаметности. В отсутствие каких-либо атак алгоритм демонстрирует безошибочное извлечение встроенной информации во всех случаях.

Предложенный алгоритм показал высокий уровень устойчивости к обозначенному выше перечню атак. Наименьшая устойчивость обнаружена в отношении атаки с выравниванием гистограммы, однако даже для данной атаки удаётся извлечь водяной знак.

Табл. 2. Значения метрики NCC для отдельных изображений и атак

Изображение	1	2	3	4	5	6	7	8
Атака	NCC
Нет	1	1	1	1	1	1	1	1
Контраст +10	1	0,9469	0,9993	0,9965	0,9984	1	1	0,9740
Контраст –10	0,9409	0,9810	0,9537	0,9625	0,9756	0,9370	0,9637	0,9842
Выравнивание гистограммы	0,8661	0,8000	0,9906	0,7959	0,9193	0,9926	0,9848	0,8895
Усиление резкости	0,9969	0,8606	0,9819	0,9484	0,9468	0,9981	0,9870	0,8792
Шум «соль-перец»	0,9801	0,9775	0,9822	0,9810	0,9815	0,9751	0,9797	0,9802
Яркость +10	1	1	1	1	1	1	1	1
Яркость –10	1	1	1	1	1	1	1	1
Добавление объекта	1	1	1	1	1	1	1	1
Кадрирование (угол)	1	1	1	1	1	1	1	1
Кадрирование (центр)	1	1	1	1	1	1	1	1
Среднее	0,9804	0,9605	0,9916	0,9713	0,9838	0,9912	0,9923	0,9734

Было выполнено сравнение полученных результатов с некоторыми другими слепыми схемами робастного встраивания невидимых ЦВЗ, использующими похожие технологии. Было выполнено встраивание аналогичного объёма информации (16 копий ЦВЗ размером 64×64 бита) в низкочастотные коэффициенты ДКП, исключая DC-коэффициент, по методу QIM с тем же шагом квантования без использования оптимизации. Как показывают результаты в табл. 4, при близких значениях метрик робастности предложенный алгоритм обеспечивает более высокие значения метрики PSNR. При использовании ГА время работы алгоритма увеличивается (8,7 с в среднем против 0,095 с для «чистого» QIM), однако это компенсируется улучшением незаметности встраивания.

Также для сравнения были выбраны алгоритм множественного встраивания ЦВЗ в область преобразований [11], алгоритм частотного встраивания на основе классического ГА [13], алгоритм частотного встраивания с применением современного алгоритма TLBO [14]. Результаты представлены в табл. 4. Новый алгоритм превосходит алгоритм [14] с точки зрения незаметности встраивания, а алгоритмы [11] и [13] по устойчивости к отдельным атакам. При этом новый алгоритм позволяет встроить ЦВЗ большего объёма, чем [13] и [14].

Табл. 3. Средние значения метрик BER и NCC

Атака	BER	NCC
Нет	0	1
Контраст +10	0,0123	0,9894
Контраст –10	0,0401	0,9623
Выравнивание гистограммы	0,1217	0,9049
Усиление резкости	0,0645	0,9499
Шум «соль-перец»	0,0228	0,9797
Яркость +10	0	1
Яркость –10	0	1
Добавление объекта	0	1
Кадрирование (угол)	0	1
Кадрирование (центр)	0	1
Среднее	0,0238	0,9806

Заключение

В данном исследовании был предложен новый алгоритм множественного встраивания ЦВЗ в гибридную пространственно-частотную область цифровых изображений с использованием ГА. Результаты экспериментов показали, что данный алгоритм обеспечивает высокую незаметность, значение метрики PSNR во всех случаях превышает 40 дБ. При этом новый алгоритм демонстрирует безошибочное извлечение ЦВЗ в отсутствие атак и показывает высокий уровень устойчивости к некоторым распространённым атакам. В дальнейшем планируется исследовать эффективность других метаэвристик для решения задачи достижения баланса между незаметностью и робастностью множественного встраивания ЦВЗ в гибридную область цифровых изображений.

а)

г)

д)

е)

Рис. 5. Примеры изображений с ЦВЗ после атак: а) уменьшение контрастности, б) добавление шума «соль-перец», в) кадрирование от угла; г) – е) соответствующие извлечённые ЦВЗ

Табл. 4. Сравнение с аналогами

ГРНТИ: 28.23.15