Mobile Robot Path Planning by RRT* in Dynamic Environments

Published Online April 2015 in MECS

This paper presents a new path planning method which helps the robot to reach the target from the beginning point without colliding fixed and mobile obstacles existing in search space. This method can be used in the environments where a camera can be installed above the searching space such as closed searching environments (large stores and factories).So it can use to guide worker robots from one point to a certain target in the manner that the robot reaches the destination without any collision with fixed and mobile obstacles in the environment. Obstacles are usually either fixed such as shelves of goods in the stores or mobile like other robots which hold specific duties. Solving the problem of finding the optimum path in map-equipped environment is a goal of search. Search problems are divided into classical and non-classical groups. Classical methods are based on Heuristic Searches. Random methods is a branch of Heuristic methods, called R* and a group of them is RRT.

According to LaVall [1], the path planning algorithms are mainly divided into two groups: 1) Compound Path planning Algorithms; and 2) Sampling-based path planning algorithms. Compound path planning algorithms are complete and they have a complicated implementation. An algorithm is considered complete if for any input it correctly reports whether there is a solution in a finite amount of time. If a solution exists, it must return one in finite time [1] . The second group is not complete but it has a simple implementation. Many sampling-based approaches are based on random sampling, which is dense with “probability complete”. This leads to algorithms that with enough points, the probability that it finds an existing solution converges to one. The most relevant information, however, is the rate of convergence, which is usually very difficult to establish [1].

The second group is divided into two other groups, namely multiple query and single query. Multiple query methods like (PRM) Probabilistic Road Map method require preprocessing while single query methods like ACA (Adrian’s clew algorithm), ESP (Expansive Space Planner), Random Walker Planner and RDT (Rapidly Exploring Dense Tree) do not need any preprocessing and are suitable for dynamic environments. One type of RDTs is called RRT which is defined in the following.

The sample-based technique for robot motion planning was introduced by Barraquand and Latombe [2]. The first sampling-based planners were not cost effective in view of operational load. Kavraki et al. and Overmars and ˇSvestka developed possible road map for path planning in configuration environments with high freedom levels [3,4,5]. Choset et al. and Hsu et al. made a comprehensive discussion on road map [6,7]. Song and Amato proved that PRM method is computationally efficient in static environments which are well-known [8]. On the other hand, this method is not suitable for dynamic environments. It does not consider vehicle dynamics of robot and it may not work in sharp rotations. Branicky et al. (2001) introduced LRM Lattice roadmap and quasi-PRM [9]. LRM was developed by Pivtoraiko et al. in order to consider dynamic restrictions [10].

RRT is one of the probabilistic path planners presented by Kuffner and Lavalle in order to solve differential problems [11,12]. The important aspect of quasi RRT algorithms is that they give conclusion to the paths that may be implemented by fundamentally dynamic systems. This algorithm is in fact a search tree which growths incrementally in the intended environment. This tree grows in the manner that at first it considers an initial amount in the start point as parent node. Then, it randomly selects a node in the space, called sampling. The distance between this node and the nodes of tree is calculated and connected to the nearest node of the tree provided that the distance is within the defined area. In this way, the search tree develops incrementally until it reaches destination. Kuffner and Lavalle proved algorithm is probabilistic complete, Hesu et al. developed RRT in the manner that it had a good convergence speed [13].

RRT and PRM have been broadly used in path planning [1,14]. The main idea of these methods includes the connection of search environments and their main difference is in their roadmap structure.

Different types of PRM are multi-query methods. Firstly it creates a graph (roadmap), to display large points with no collision. Then, it responds to questions by calculating the shortest path from start point to destination. Later it was shown that this algorithm was probabilistic complete [15]. During the recent decade, PRM algorithm was concentrated on robotic researches. Several studies have developed this algorithm [9,16,17].

Although multiple-query methods are valuable in highly structured environments such as factory floors, most online planning problems do not require multiple queries. For instance, the robot moves from one environment to another, or the environment is not known a priori. In addition, in some of these applications the initial calculation of a roadmap is mostly computationally expensive or even infeasible. Incremental sampling-based algorithms were developed as online matches of PRM proportional to these applications [12, 18]. The incremental nature of this algorithm results in a prompt solution. In addition, partial changes in the environment do not need any plan from the beginning because most paths still may not be implemented (this is the characteristics of most roadmaps). This characteristic results in a significant saving in calculations in prompt online implementation.

RRT is an algorithm which has been extensively studied. Its positive advantages include probabilistic complete [12] and the probability of failure decays to zero exponentially [19]. It has several functions in different fields such as robotic, etc. [20,21,19,22]. In particular, RRTs have been shown to work effectively for systems with differential constraints, nonlinear dynamics, and non-holonomic constraints, as well as purely discrete or hybrid systems [23,24,22].

Barraquand and Latombe [1] have introduced one of random motion planners. This planner combines potential descending gradient with random walk procedure processor to escape from spurious local minima. RPP is one of the most important algorithms for motion planning (this algorithm solved problems with high freedom degrees and was more advanced than other planners at that time). RPP method is probabilistic complete and provides good results. Currently it has been found that this planner is unable to solve problems on passing through narrow paths.

Ariadne’s Clew Algorithm (ACA) expands search tree such that in each repetition it explores new zones as much as possible. There are two phases, namely Search and Explore search? Which are replaced in consecutive repetitions. Search phase is used to determine sub-targets or addresses used in C, C is the entire search space, and Explore phase distributes theses addresses at the end of a path, originated from the primary configuration [26]. The drawback of this method is that the executed optimized process by Explore is costly and requires regulating many parameters.

Expansive-Space Tree (EST) planner [17,27] has certain ideas in common with PRM methods. It tries to sample a part of C, which is related to a specific issue and avoids pre-calculated cost of roadmap for the total free area. The aforesaid Algorithm iteratively executes two phases like ACA: Expansion and Connection. This is a bidirectional planning (i.e. it makes two trees). Moreover, a unidirectional copy of that has been implemented as well.

Single query, Bidirectional Lazy collision checking (SBL) planner is another method extracted from probable roadmap for single-query planning problems. In this case, the roadmap does not cover the whole C. The idea of this algorithm is to exploit the delay in examining collision by its combination with comparative sampling method similar to what used by EST. The planner searches F by building a roadmap made of two trees of nodes, T s and T g. The root of T s is the start configuration q s and the root of T g is the target configuration of q g (it means uses the search of bidirectional search). F is a part of C space that is empty of obstacles. Each new node formed during the planning is installed in one of the two trees as a sub-set of an already existing node. Two nodes connected by the straight line in C. This algorithm is used in an issue which includes number of manipulators arms works in the same workspace [28].

Further development of Rapidly-exploring Random Graph (RRG) is RRT [2]. This algorithm is introduced as an incremental algorithm for making a connected path map (probably includes ring). RRG algorithm in the first attempt tries to connect the nearest node to the new sample, similar to RRT. If this act is successful, the new node will be added to the set. Graph of RRT (direct tree) is a sub graph of RRG graph (indirect graph probability of inclusion of ring). In particular two graphs have the same set of nodes and the edges set of RRT graph is a sub set of edges set of RRG graph.

In this article RRT* algorithm is used to find a feasible path from the start point to the predetermined goal point. The application of this algorithm is like RRT with a difference that the path result is asymptotically optimal. To decide either adding or not adding the randomly selected node to tree the distance the node from all nodes of tree till the start point will be calculated and the node with least distance will be selected. Also, to avoid fixed and moving obstacles, image processing techniques with a camera is used. Simulation results indicate that the algorithm used to perform well in dynamic environments and answer is optimal in terms of distance and time.

This paper is organized as fallows. In the second section, there is a brief description of RRT* algorithm and its advantages, in addition it is mentioned how to tune parameters of RRT*. In the third section there is an introduction of method which presented for avoiding fixed obstacles collision and is described how to use image processing techniques and path prediction of moving obstacles. In the fourth section, introduction of method presented for the concordance of designed dynamic path and movement of moving obstacles after that simulation and results are described. Finally the efficiency of RRT* is improved and concluded.

• II.    RRT* Algorithm

Maintaining and obtaining the tree structure rather than a graph is not economical in term of memory requirements. Algorithm of RRT is resulted by defining RRG with a difference that the additional edges like edges which the section not from the shortest path from the root till the head of tree, is deleted and formation of ring is avoided. Graphs of RRT and RRT* are trees of a single root and common set and set of edges which is the sub set of RRG and guarantees under rewiring function which the set is connected to each other with least cost [31]. The algorithm of RRT in form of pseudo code shown below. The procedure of this algorithm is in such a manner that like RRT and RRG increase the point in the set on stochastic form. Also, consider the connection of new node to the set of . But all possible connection not added to the E edges set. In particular in the first instance an edge is created from set which can be connected to under the path with least expense and secondly if the path of having less expense in comparison to path from its present parent, new edge created from to set. In this case the linked edge will be deleted to present parent in order to achieve the structure of tree.

Г ^ Initialize Tree ();

Г ^ Insert Node (Ф, z .., Г)

for i =1 to i=N do z ; .; ^ Sample (i)

-"К'бЯ ^ Nearest (Г,      )

if Obstacle Free (     ) then

• -      ■  ^ Near ^(Г, -  - ; .<  '•  )

^min ^7 Choose Parent ⁽_ ._.-,- . ,_ ■ _- - -.-_-- ,

);

Г ^ Insert Node ( _ - .,_.,. , Г );

Г ^ ReWire (Г , J _;f, . z ,. _;,J ._{л ;X} ); return

First line is initialize of search trees, third line select stochastic sample from search space, the fifth line finds the nearest node from the trees to the selected stochastic node and in sixth line in cased the selected stochastic sample in the free of obstacles space, will be added to tree. In the tenth line, if another node from the tree for the new stochastic node, having shorter path to the root, it will be selected as a father node of stochastic node.

Whatsoever presented in this article, is a composition of method of path planning with image processing techniques. Also, using other distance measuring metrics for measuring the distance between stochastic samples selected in search space and nodes of search tree. Using search distance indeed in place of Euclidean distance metric has helped in solving issue with shortest path and complication of shortest time and location. As shown in fig.1, implementation of RRT* algorithm in an environment with a dimension of 10x10 and start point (0, 0) and goal point (10 and 10) and without obstacle. As clear, tree is expanded to the entire space (in blue color) and paths will be check for rewiring in (cyan) color and path shown with red color.

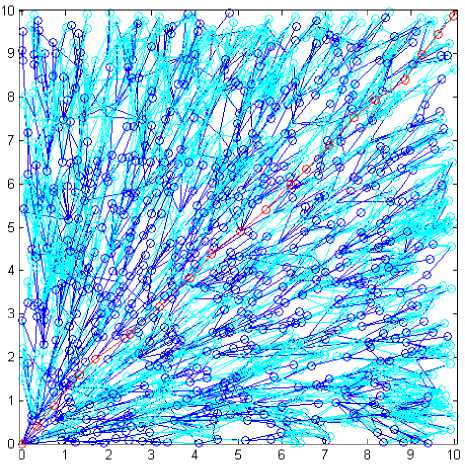
Fig. 1. RRT* in free space

As it has been seen there is several parameters which need to be tune in order to have optimize result. Distance metric and number of samples are two parameters that are studied in this paper. The purpose is to find a relative amount between these two parameters which guide the robot to an answer which is optimum in aspect of time and computation efficiency, path smoothing and length of path.

Using different standard distances can affect the distance of planned path and time for path computation. In this experiment, three metrics for distance computation are examined: Chebyshev, Euclidean, and City Block.

Euclidean distance between two points of “a” and “b” in an environment with two dimension is computed as follows:

Euclidean distance metric:

J(x2 - xi)2 + (y2 - У1)2

City Block distance metric:

(Ix2 -xil + |У2 -У11)

Chebyshev distance metric:

Max {|x2 -xj,|y2 -У1}

Based on application any of them can be suitable. When the system needs to be real-time it can be easily done with Chebyshev distance metric cause of easy formulate.

Moreover number of samples is an important parameter and can have high influence on the system. Due to high number of samples, the system will find the path in longer time but the path will be smoother and due to low number of samples, the system will find the path fast but not good in smoothing.

• III.    Obstacles Avoidance

The system before planning the path uses image processing techniques to identify the position of fixed obstacles and avoid collision obstacles. The procedure identifies the position of fixed obstacles with stickers via a camera. So in first step the RRT* algorithm samples a node in space then check if it is in free space of identify as an obstacle and in case the sample selected from space occupied by obstacle, search tree will delete it and select another sample. In this way it is possible to design a path without any obstacle.

In this section RRT* algorithm was implemented in an environment with moving obstacles, which was executed in two phases: first prediction of moving obstacles and second: phase synchronization of moving obstacles and path planner system in many tiny offline part which seems on-line and can be used in real time systems.

• A.    Position and time Prediction of moving obstacles

To avoid collision moving obstacles which have repetitive moving patterns like circular movement pattern, movement pattern towards straight line or sinusoidal form movement pattern and so the movements will be predictable the system used image processing techniques so it is possible to estimate the moving speed of objects and their future position in the specific time. In such a manner that the picture is video form and it will be transferred to image processing system through camera installed on the ceiling and tracking the present movement of the obstacles. Moreover image processing techniques estimate present and future locations of obstacle. In this way we will be able to estimate and predict the possibility of collision between mobile robots with moving obstacles.

• B.    Synchronization

After recognizing the situation of fixed obstacles in search environment and prediction of the movement of moving obstacles, a programmed system studies the feasibility of the probable contact of a mobile robot and available moving obstacle in the environment; and based on that will decide to plan another path. As all paths will locate in a specific area for optimizing the asymptotic paths and moving obstacles follow a repetitive pattern on their movement; so, in next steps, planning will be done by algorithm RRT* in the area recognized with the probability of contact and obstacles are considered as fixed one and a new path is planned.

Identify fixed objects and moving objects

Estimate the position related to any time segment of mobile obstacles

Check for probably collision between obstacles and mobile robot

I

--------► RRT* paths a path |

Fig. 2. Flowchart of suggested algorithm

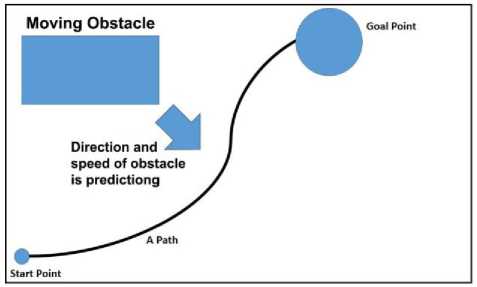
Fig. 3. It is shown an initial path named A that is planned without considering the future position of obstacle

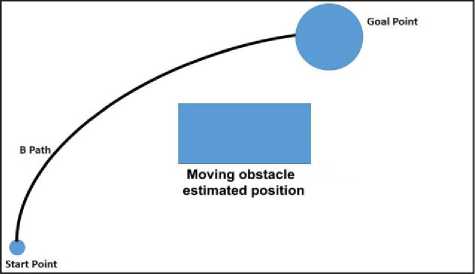
Fig. 4. It is shown path named B that is planned with considering the future position of obstacle

• V. Conclusion

• IV. Simulation

All simulations are performed in the MATLAB environment and image processing techniques are simulated by using Matlab image processing toolbox.

• A.    Environment

In simulations, an environment of 10×10 is considered with a relatively complex map.

Fig.5 shows the map used in simulations.

Fig. 5. A random complex map

• B.    Number of samples

  Different number of sampling (50000, 300000, 10000, 5000, and 100000) have been tested for the same map. Sampling number of more than 30000 needs more time for computing while it has no marked effects on shortening the path. For this reason, high number of sampling is not recommended except for the cases that robot needs smooth paths due to the differential limitations.

• C.    Appropriate measurement standard

Using different standard distances can influence path length distances and time for path computation too. In this test, three metrics for distance computation are examined: Chebyshev, Euclidean, and City Block.

Using Euclidean distance metric is more reliable due to its less metric deviation for the travelled distance, but the shortest distance can be achievable through measurement metric of Chebyshev distance. Moreover, the results from City Block distance measurement metric were more unreliable than other two metrics. If the aim is finding a path in at least time and distance is not determining, sampling number of 10000 and distance metric of City Block is appropriate. However, it depends on the condition of the considered robot, and the speed. Moreover moving capability, appropriate measurement, and proper number of sampling can be chosen in a way that distance and time reach optimized executable path.

It should be also considered that in environments with mobile obstacles which require REAL TIME planning, parameter of time is very determining and pivotal. Chebyshev distance metric has a simple mathematics formula which makes the computation easier and is more optimized regarding the other two metrics in the viewpoint of time consuming. But, it has more diffusion and metric deviation regarding the Euclidean distance metric which makes it less reliable.

In this study a method is provided for planning mobile robots in indoor environments such as stores or factories. This method is a combination of algorithm of asymptotic optimal Rapidly-Exploring Random Tree (RRT*) for mapping the executable path with image processing techniques in MATLAB for recognizing the situation of fixed and moving obstacles in different times. As it is shown in results, the provided method has proved its efficiency and mobile robot can move in environment without contacting fixed and moving obstacles in environment and get to the specific point.

Fig. 6. Examples of RRT* implementation on a relatively complex map for 10 reputation. in a) , b) , c) number of samples is 10000; in d) , e), f) number of samples is 30000; in g) , h) , i) number of samples is 100000; in a) , d) , g) paths are calculating by Euclidean distance metric; in b) , e)

, h) paths are calculating by Chebyshev distance metric; in c) , f) , i) paths are calculating by City-Block distance metric

Table 1. RRT* algorithm with 10000 sampling number

	Longest path	Shortest path	Standard deviation	Path length advantage
Chebyshev	234/07	135/63	23/85	170
Euclidean	255/50	168/62	11	188/33
City Block	308	131	23	243/93

Table 2. RRT* algorithm with 20000 sampling number

	Longest path	Shortest path	Standard deviation	Path length advantage
Chebyshev	213/12	146/64	11	163/63
Euclidean	204/15	165/90	8	178/39
City Block	296	212	16	238/20

Table 1. RRT* algorithm with 10000 sampling number

	Average Length of path	Number of seen nodes	time
Chebyshev	167.62+9.05, 167.62-9.05	2075+138, 2075-138	1.31+0.25, 1.31-0.25
Euclidean	191.83+6.62, 191.83-6.62	5479+176, 5479-176	2.02+0.42, 2.02-0.42
City Block	229.50+76.80, 229.50-76.80	1975+228, 1975-228	1.12+0.15, 1.12-0.15

Table 2. RRT* algorithm with 30000 sampling number

	Average Length of path	Number of seen nodes	time
Chebyshev	169.46+11.35, 169.46-11.35	2813+320, 2813-320	4.49+0.61, 4.49-0.61
Euclidean	179.90+6.55, 179.90-6.55	9129+403, 9129-403	4.66+3.11, 4.66-3.11
City Block	236+7.18, 236-7.18	4184+278, 4184-278	6.56+1.10, 6.56-1.10

Table 3. RRT* algorithm with 50000 sampling number

	Average Length of path	Number of seen nodes	time
Chebyshev	171.78+11.45, 171.78-11.45	2789+243, 2789-243	3.09+0.78, 3.09-0.78
Euclidean	188.40+9, 188.40-9	9430+332, 9430-332	6.82+2.37, 6.82-2.37
City Block	250.80+12.96, 250.80-12.96	4549+372, 4549-372	6.88+3.23, 6.88-3.23

Table 4. RRT* algorithm with 100000 sampling number

	Average Length of path	Number of seen nodes	time
Chebyshev	169.64+13.45, 169.64-13.45	2856+248, 2856-248	6.67+1.88, 6.67-1.88
Euclidean	186.18+8.86, 186.18-8.86	10075+544, 10075-544	14.86+5.80, 14.86-5.80
City Block	237.80+18.65, 237.80-18.65	4435+355, 4435-355	26.44+9.52, 26.44-9.52