Мобильное приложение для поиска оптимального маршрута в университетском городке

Крупные университеты имеет сложную архитектурную планировку, поэтому для обучающихся и гостей университета задача поиска нужной аудитории является актуальной. Например, университетский городок Оренбургского государственного университета (ОГУ) состоит из 14 учебных корпусов и сотен различных аудиторий [1].

В настоящее время активно используются навигационные сервисы в открытом пространстве во многих сферах деятельности. Всё большую актуальность приобретает навигация, основанная на использовании мобильных приложений (МП), что обусловлено доступностью мобильных устройств [2]. В контексте рассматриваемой проблемы наиболее известны следующие МП для пешей навигации: «Яндекс Карты» [3], 2ГИС [4], Google Maps [5], HERE WeGo [6], Maps.me [7], Sygic GPS Navigation [8], Magic Earth Navigation & Maps [9], iGO Navigation [10], OsmAnd [11], MapFactor Navigation [12].

Результаты проведённого анализа основных характеристик названных МП в виде выявленных достоинств для данной задачи приведены в таблице 1. Среди недостатков некоторых из рассмотренных МП можно отметить: притормаживающий пользовательский интерфейс; устаревшая графика; наличие рекламы; не возможность поиска оптимального пути и др. По информации из открытых источников удалось лишь установить, что в МП [3] для построения маршрутов используется алгоритм Дейкстры.

Таблица 1 – Основные характеристики и достоинства МП

Мобильное приложение название, разработчик, сайт, платформа	Достоинства
Яндекс. Карты Яндекс mobile.yandex.ru/apps/maps Android; iOS	■    позволяет строить маршруты для пешеходов; ■    знает короткие пути через дворы и проходы между зданиями; ■    показывает входы в здания и включает поэтажные схемы; ■    имеет голосовой помощник «Яндекс. Алиса».
2ГИС ДубльГИС info.2gis.com Android; iOS; Wear OS	■    умеет прокладывать самые короткие пешие маршруты; ■    может работать без подключения к Интернету; ■    отображает поэтажные схемы торговых центров (ТЦ), вокзалов и аэропортов; ■    содержит путеводитель с информацией о городских достопримечательностях и интересных местах.
Google Maps Google google.com/maps Android; iOS	■    позволяет строить пешие маршруты и знает расписание общественного транспорта; ■    поддерживает технологию дополненной реальности (можно видеть подсказки поверх изображения окружающей местности); ■    предоставляет возможность просмотра панорамных снимков и схем, которые помогают ориентироваться в больших зданиях (аэропорты, вокзалы, ТЦ и др.); ■    поддерживает голосовое управление и сохранение карт в памяти устройства с целью последующего использования без подключения к Интернету.
HERE WeGo Here Technologies here.com Android; iOS	■    за считаные секунды подбирает доступные варианты перемещения из начальной точки в конечную, рассчитывает примерное время в пути и позволяет выбрать оптимальный маршрут из списка; ■    при навигации может переключаться в 3D-режим; ■    имеется возможность сохранения карт в памяти мобильного устройства и использования приложения в автономном режиме.
Maps.me Maps.me Limited maps.me Android; iOS	■    построен на основе свободной географической карты OpenStreetMap; ■    картографические данные можно скопировать в память мобильного устройства и пользоваться приложением без подключения к Интернету; ■    умеет строить пешие и велосипедные маршруты.
Sygic GPS Navigation Sygic sygic.com/gps-navigation Android; iOS	■ поддерживается поиск по организациям.
Magic Earth Navigation & Maps General Magic magicearth.com Android; iOS	■    построен на основе свободной географической карты OpenStreetMap; ■    предусмотрен выбор альтернативных маршрутов и справочник организаций; ■    присутствует функция «Что находится рядом», которая выводит список близлежащих объектов.
iGO Navigation NNG Software Developing and Commercial igonavigation.com Android; iOS	■ позволяет строить маршруты для пешеходов и автомобилистов.
OsmAnd OsmAnd osmand.net Android; iOS	■    построен на основе свободной географической карты OpenStreetMap; ■    предоставляет возможность получения ежечасных обновлений карт; ■    имеет встроенный путеводитель; ■    ведет запись маршрута.

Все рассмотренные МП преимущественно ориентированы для навигации на открытой местности большой площади. При этом внутреннюю навигацию в них предполагается ис- пользовать для известных крупных сооружений (большие ТЦ, вокзалы, государственные учреждения и др.) с большими потоками людей. Учебные корпуса университетов, как правило, локализованы на территории небольшой площади. Это означает, что многие функции, заложенные в указанных навигационных сервисах, не будут использованы, а возможность добавления карт требуемых зданий может быть сопряжена с угрозой ослабления безопасности университета. При этом требуется обеспечить большую точность для построения маршрутов в случаях, когда исходная и искомая точки маршрута находятся в разных корпусах или на разных этажах. Важное значение может иметь отыскание оптимального маршрута внутри здания без выхода на улицу, например, в зимнее время года. Поэтому для поиска оптимального маршрута в университете требуется навигационный сервис, учитывающий перечисленные факторы.

Целью исследования является разработка МП для поиска оптимального маршрута в университетском городке.

Для достижения поставленной цели необходимо:

• ■    сформулировать математическую задачу в виде поиска кратчайшего пути в графе;

• ■    выбрать алгоритм поиска кратчайшего пути в графе;

• ■    разработать логическую архитектуру программы МП;

• ■    разработать вспомогательный сервис для добаления новых карт в МП;

• ■    проверить работоспособность МП.

1    Постановка задачи и метод решения

Задачу поиска оптимального пути от исходной точки u до искомой аудитории v можно представить как известную задачу поиска кратчайшего пути в графе [13, 14]. Такой подход используется в рассмотренных МП [3-12].

Пусть задан ортограф G ( V, A ), каждой дуге которого ( u,v ) ставится в соответствие число L(u,v) – длина дуги. Под длиной дуги маршрута (пути) понимают сумму дуг, составляющих маршрут. Требуется найти длины кратчайших маршрутов и маршруты от выбранной вершины u до всех остальных вершин графа v i .

Наиболее известными алгоритмами поиска кратчайшего маршрута в графе являются: алгоритм поиска в ширину, жадный алгоритм поиска кратчайшего пути, алгоритм Дейсктры [15, 16]. В таблице 2 приведены результаты сравнительного анализа указанных алгоритмов.

Таблица 2 – Результаты сравнительного анализа алгоритмов отыскания кратчайшего пути в графе

Алгоритм	Достоинства	Недостатки
Алгоритм поиска в ширину	■   сравнительная простота ре ализации ■   полнота и оптимальность	■ при увеличении пространства поиска производительность поиска снижается по сравнению с другими эвристическими алгоритмами
Жадный алгоритм поиска	■ простота поиска оптимального решения	■ сложность оценки алгоритма
Алгоритм Дейкстры	■ сравнительная простота реализации	■ находит кратчайшие пути и их величины только от одной вершины

В качестве основы для построения математической модели задачи принят алгоритм Дейкстры. Программная реализация построена на основе UML -шаблонов проектирования [17, 18]. Архитектура программного средства BLoC (компонент бизнес-логики, от англ. Business Logic Component ), идея которой заключается в разделении интерфейса ( UI -компонента, от англ. User Interface ) и бизнес-логики приложения, соответствует единой системы программной документации [19].

Для взаимодействия с пользователем требуются следующие визуальные элементы управления:

• ■    поле выбора начальной и конечной точек маршрута;

• ■    кнопки старта и сброса маршрута;

• ■    кнопки для пролистывания этапов следования по маршруту;

• ■    кнопки, отвечающие за масштабирование и ориентацию карты;

• ■    поле для отображения карты и рассчитанного маршрута;

  

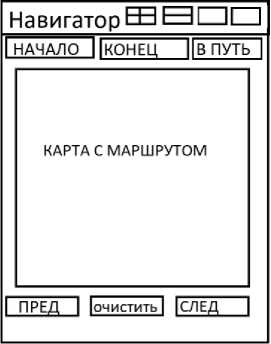
  Рисунок 1 – Вкладка «Навигация» МП

  
  

• ■    выпадающий список для выбора отображаемой карты.

Для работы интерфейса требуются классы, в которых реализованы алгоритмы: поиска путей, взаимодействия с базой данных (БД), отображения карт и дополнительной информации, работы с вре́менными данными. Термин «класс» в данном случае используется в контексте объектно-ориентированного программирования и подразумевает собой шаблон для создания объектов, обеспечивающий начальные значения состояний: инициализация полей-переменных и реализация поведения функций или методов. Это позволяет создать универсальный программный продукт для различных карт.

На рисунке 1 представлена вкладка «Навигация» МП. Первый UI -компонент (визуальный элемент интерфейса МП) отвечает за верхнюю часть экрана, в котором расположены наименование вкладки и кнопки, отвечающие за масштаб и ориентацию карты, а также выпадающий список, из которого можно выбрать карты для просмотра. Во второй UI -компонент, имеющий табличную структуру, вложена группа UI -компонентов. В первой строке таблицы расположены два текстовых поля с выпадающим списком, с помощью которых пользователь может выбрать начальную и конечную точки для прокладывания маршрута, и кнопка, отвечающая за расчёт маршрута и его отображение. Во второй строке таблицы расположен UI -компонент, на котором отображается карта и путь, который будет рассчитан МП.

Карты используются в автономном режиме, т.к. все необходимые данные хранятся в приложении, и расчёт оптимального пути не требует подключения к сети Интернет, а выполняется на устройстве пользователя.

Заключительная строка таблицы содержит три кнопки:

• ■    предыдущее действие (если путь проложен не только на одном этаже, а затрагивает переходы между этажами и корпусами);

• ■    очистить (стирает маршрут из памяти и экрана, а также блокирует соседние кнопки);

• ■    следующее действие (если путь проложен не только на одном этаже, а затрагивает переходы между этажами и корпусами).

2    Описание и проверка работоспособности МП

В качестве среды для разработки МП выбрана платформа Android Studio 1 . Для разработки программного продукта использовался объектно-ориентированный язык Flutter 2 . Выбранный язык является кроссплатформенным языком, что позволяет создавать МП под Android и iOS , а также для решений под Windows, macOS и Linux с использованием языка

• ¹    Android Studio. https://developer.android.com/studio .

• ²    Flutter. https://flutter.dev/ .

программирования Dart 3 . В языке Dart нет готового инструмента для отображения карт, но с помощью доступного функционала можно создать новый функционал, отвечающим заданным требованиям.

Для разработки МП был создан шаблон данных, который отображается на экране устройства. С помощью встроенного во фреймворке Flutter инструмента, в котором реализован функционал отображения примитивных геометрических фигур (точка, линия, окружность) и окрашивания их в любой цвет, написан класс, обрабатывающий входной многомерный массив данных и отображающий результат на карте. На рисунке 2 приведён пример шаблона данных, в котором:

[массив точек карты], [массив точек карты], [массив точек графа], [массив точек легенды карты], [таблица смежности графа],

Рисунок 2 – Шаблон данных

• ■    массив точек карты - стены здания;

• ■    массив точек карты - стены внутренней планировки помещений в здании;

• ■    массив точек графа - дороги (возможные маршруты);

• ■    массив точек легенды карты - местонахождение пронумерованных аудиторий (корпусов и др.);

• ■    таблица смежности графа - указание путей между аудиториями (корпусами и др.), являющихся вершинами графа.

На рисунке 3 показан пример шаблона данных МП, принимающего входные данные и отображающего возможные маршруты внутри помещения, с нумерацией аудиторий. Для разработки программного обеспечения выполнена предварительная работа на базе предоставленных ОГУ документов о планировке корпусов и актуальной информации о расположении аудиторий и иных помещений. Подготовленный материал форматирован к виду, соответствующему шаблону данных. Полученный результат помещён в БД, которая размещена на удалённом сервере. В интерфейсе поля, отвечающего за выбор начальной и конечной точек маршрута, происходит наполнение информацией из БД, т.е. из полей легенды карты при старте программы. Когда пользователь совершает выбор, то данные записываются во вре́менные переменные, описанные в логической архитектуре, представляющей собой объ- ектно-ориентированную программы, которая содержит слои, классы объектов, пакеты, основные платформы, интерфейсы, подсистемы и их взаимодействия.

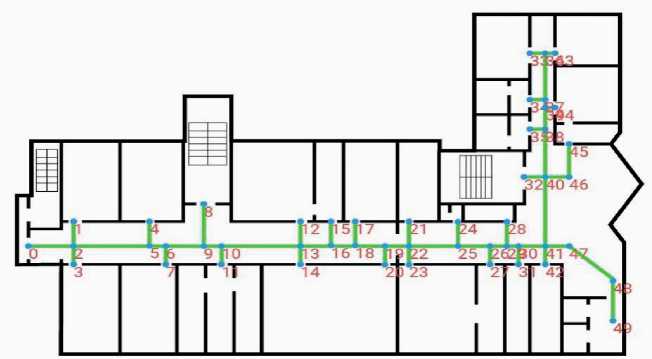
Рисунок 3 – Пример шаблона данных мобильного приложения

На рисунке 4 приведён пример выбора начальной точки маршрута. В интерфейсе предусмотрен выпадающий список, из которого пользователь может выбрать нужную карту для отображения. Результат записывается во врѐменную переменную, описанную в логической ар- хитектуре, и передаётся в класс для отображения. Пример выпадающего списка представлен на рисунке 5.

• ³     https://dart.dev/ .

Для проверки работоспособности МП проведён эксперимент, согласно которому требуется построить кратчайший путь от 16-го корпуса до аудитории 20119, расположенной в 20ом корпусе на 1-ом этаже. На рисунке 6 представлена карта результата эксперимента.

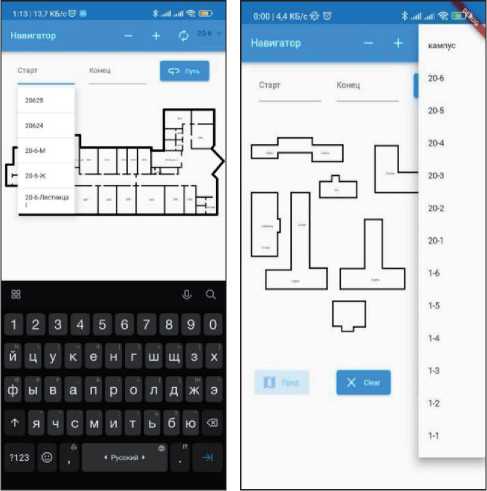
Рисунок 4 – Пример выбора начальной точки маршрута

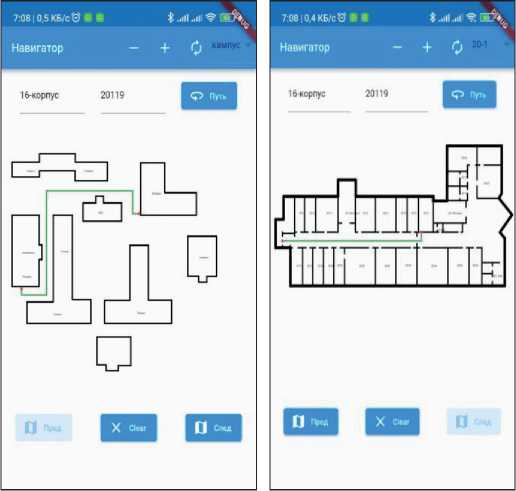
а                            б а – маршрут между корпусами; б – маршрут в корпусе

Рисунок 6 – Карта результата эксперимента

Рисунок 5 – Пример выпадающего списка

На рисунке 7 приведён построенный МП маршрут, на котором числа означают последовательность точек графа, через которые проходит путь.

I/flutter (18921): Начало маршрута: 16-корпус зайдите в: 28-корпус

I/flutter (18921): Маршрут: 26 25 27 28 38 32 2 3 6 7 8

I/flutter (18921): идите от входа до конца маршрута: 28119

I/flutter (18921): Маршрут: 8 2 3 6 7 9 11 13 16 17 19 21 24 26 29 31 33

Рисунок 7 – Построенный мобильным приложением маршрут эксперимента

Для упрощения добавления новых карт в БД МП, разработан вспомогательный сервис, написанный на языке программирования PHP 4 , который преобразует SVG картинку 5 в набор данных по созданному шаблону.

SVG -изображение имеет следующую структуру:

• ■    1 слой - стены здания;

• ■   2 слой - стены внутренней планировки помещений;

• ■   3 слой - дороги (возможные маршруты);

• ■   4 слой - местонахождение точек графа (окружности малого диаметра);

• ■   5 слой - местонахождение пронумерованных аудиторий, корпусов и иных помещений

(окружности большого диаметра).

• ⁴    Lerdorf, Rasmus (June 8, 1995). Announce: Personal Home Page Tools (PHP Tools). Retrieved 7 June 2011.

• 5    SVG (от Scalable Vector Graphics — масштабируемая векторная графика) — это вид графики, которую создают с помощью математического описания геометрических примитивов, которые и образуют все детали изображения.

На рисунке 8 представлен пример изображения карты возможных маршрутов, которая обрабатывается вспомогательным сервисом.

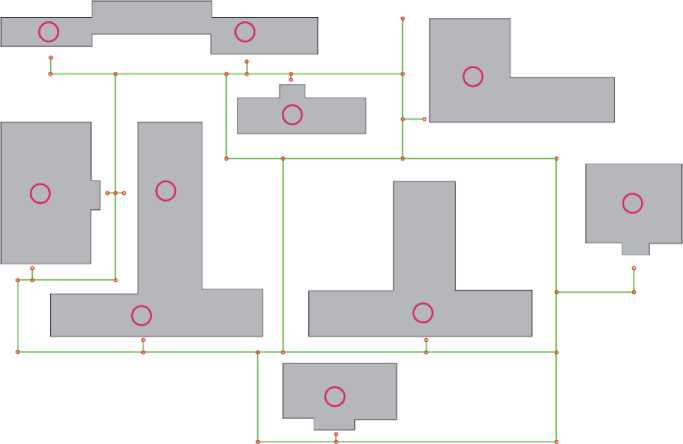
Рисунок 8 – Карта возможных маршрутов

Корпус или аудитория

Название корпуса или аудитории

О Вершина графа])

дорога(возможный маршрут)

Сервис поочерёдно обрабатывает слой и выдаёт данные согласно шаблону, после чего они интегрируются в МП.

На рисунке 9 приведена структура SVG -изображения, полученная за счёт обработки данных о планировке помещений и актуальной информации. На основании слоёв 3 и 4 за счёт работы скрипта PHP генерируется таблица смежности графа, приведённая на рисунке 10. На вход подаются данные, представленные на рисунке 9, вычисляются растояния между точками, на основании бинарных отношений принадлежности точек прямым и пересечений прямых определяются ближашие соседи для всех вершин (рассматривает маршруты, проходящие через окружности из слоя 4 и отыскиваются ближайшие окружности, через которые проходят эти дороги).

cx=196.5 cy=168.5 r= 3.5 /> cx="195.5" cy="205.5" r=’3.5"/> cx="342.5" cy="205.5" r="3.5"/> cx="342.5" cy="474.5" r="3.5"/> cx='324.5* cy="474.5" r="3.5"/> cx="361.5" cy="474.5" r="3.5"/> cx="343.5' cy="670.5" r="3.5"/> cx="154.5* cy="670.5" r="3.5"/> cx="154.5" cy="643.5" r="3.5"/> cx="121.5" cy="670.5" r="3.5"/> cx="121.5" cy="832.5" r="3.5"/> cx="405.5" cy=“833.5" r="3.5"/> cx="4A5.5" cy=“805.5" r="3.5"/> cx="664.5" cy="833.5" r="3.5"/> cx="721.5" cy="833.5" r="3.5"/> cx="664.5" cy="1035.5" r="3.5"/> cx="841.5" cy=“1035.5" r="3.5"/> cx=*841.5" cy=“1018.5" r="3.5"/> cx='1339.5* cy="1035.5" r="3.5"/> cx='1339.5" cy="833.5" r="3.5"/> cx="1044.5" cy="833.5" r="3.5"/> cx="1044.5“ cy="805.5" r="3.5"/> cx="721.5" cy="396.5" r="3.5"/> cx="593.5" cy="396.5" r="3.5"/> cx="991.5" cy="396.5" r="3.5"/> cx="991.5" cy="307.5" r="3.5"/> cx="1040.5“ cy="307.5" r="3.5"/> cx="991.5" cy=“205.5" r="3.5"/> cx="739.5" cy="205.5" r="3.5"/> cx="739.5" cy="218.5" r="3.5"/> cx="639.5" cy="205.5" r="3.5"/> cx="639.5" cy=“177.5" r="3.5"/> cx="593.5" cy=“205.5" r="3.5"/> cx="991.5" cy="80.5" r=*3.5"/> cx='1339.5" cy="396.5" r="3.5"/> cx='1339.5" cy="697.5" r="3.5"/> cx="1514.5“ cy="697.5" r="3.5"/> cx="1514.5“ cy="643.5" r="3.5"/>

: [0,1,0,e,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,0,0,0,0,0,0,0,0,0,0,0,0,0,0,], . [1,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,], ■ [0,1,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,], [0,0,1,0,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,0,0,0,0,0,0,6,0,0,0,0,0,0,0,], । [0,0, 0,1,0,0, 0,0,0,0, 0,0, 6,0,0,0,0,0, 0,6,0,0,0, 0,0, 0,6, 0,0, 0,0, 0,0, 0,0,0,0,0,], ’ [0,0, 0,1,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,], [0,0,0,1,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,], ' [0,0,0,6,0,0,1,0,1,1,0,0, 0,0,0,0,0,0,0,0,0,0,0,6,0,0,0,0,0,0,6,0,0,0,0,0,0,0,], ' [0,0, 0,0,0,0, 0,1,0,0, 0,0, 0,0,0,0,0,0, 0,0,0,0,0, 0,0, 0,0, 0,0, 0,6, 0,0, 0,0,0,0,6,], [0,0,0,0,0,0,0,1,0,0,1,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,], : [0,0,0,0,0,0,0,0,0,1,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,], ■ [0,0,0,6,6,0,0,0,0,0,1,0, 1,1,0,0,0,6,0,0,0,0,0,0,6,0,0,0,0,0,6,0,0,0,0,0,0,0,], [0,0, 0,0,0,0, 0,0,0,0, 6,1, 0,0,0,0,0,0, 0,0,0,0,0, 0,0, 0,0, 0,0, 0,6, 0,0, 0,0,0,0,6,], [0,0, 0,0,0,0,0, 0,0,0,0, 1,0,0, 1,1,0,0, 0,0,0,0,0,0,0, 0,0,0,0,0, 0,0, 0,0, 0,0, 0,0,], I [0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,1,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,], [0,0,0,6,0,0,0,0,0,0,0,0,0,1,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,6,0,0,0,0,0,0,0,], [0,0, 0,0,0,0, 0,0,0,0, 0,0, 0,0,0,1,0,1, 1,0,0,0,0, 0,0, 0,0, 0,0, 0,6, 0,0, 0,0,0,0,6,], I [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,], I [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0, 0,0, ], [0,0,0,6,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,], [0,0, 0,0,0,0, 0,0,0,0, 0,0, 0,0, 1,0,0,0, 0,1,0, 1,0, 0,0, 0,0, 0,0, 0,6, 0,0, 0,0,0,0,6,], . [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,], ■ [0,0,0,0,0,0,0,0,0,0,0,0, 0,0,1,0,0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,], [0,0,0,6,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,6,0,1,0,0,0,0,0,], । [0,0, 0,0,0,0, 0,0,0,0, 0,0, 0,0,0,0,0,0, 0,0,0,0,1,6,0, 1,0, 0,0, 0,0, 0,0, 0,1,0,0,0,], ’ [0,0, 0,0,0,0,0, 0,0,0,0, 0,0,0,0,0,0,0, 0,0,0,0,0,0,1, 0,1,1,0, 0,0, 0,0,0, 0,0, 0,0,], [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,], ' [0,0, 0,6,6,0, 0,0,0,0,0,0, 0,6,0,0,0,6, 0,0,0,0, 0,0,6,1,0,0,1, 0,6, 6,0, 1,0,0,0,0,], I [0,0, 0,0,0,0, 0,0,0,0, 0,0, 0,0,0,0,0,0,0, 0,0,0,0, 0,0,0,0,1,0,1,1,0,0, 0,0,0,0,6,], [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0, 0,0,0,0,0,0,], : [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,1,1,0,0,0,0,0,], ■ [0,0, 0,6,6,0,0,0,0,0,0,0, 0,6,0,0,0,6,0,0,0,0,0,0,6,0,0,0,0,0,1,6,0,0,0,0,0,0,], [0,0, 1,6,0,0, 0,0,0,0, 0,0, 0,0,0,0,0,0, 0,0,0,0,0, 1,0, 0,0, 0,0, 0,1, 0,0, 0,0,0,0,6,], [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,], I [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,1,0,0,], [0,0, 0,6,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,6,0,0,0,1,0,1,0,], [0,0, 0,0,0,0, 0,0,0,0, 0,0, 0,0,0,0,0,0, 0,0,0,0, 0,0, 0,0,0,0,0,0, 6,0, 0,0, 0,1, 0,1,], I [0,0, 0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0, 0,0, 0,0,0,0,0,0, 0,0, 0,0, 0,0, 1,0,],

]J

Рисунок 9 – Структура SVG-изображения

Рисунок 10 – Таблица смежности

Заключительным этапом работы вспомогательного сервиса является выгрузка конечного результата в БД, которая расположена на удалённом сервере.

Заключение

Разработано МП для поиска оптимального маршрута от начальной точки до точки назначения с функционалом, призванным создать благоприятные условия для удобной навигации в университете. Новизна предложенной разработки заключается в универсальности средств отображения, добавления и редактирования карт. Дальнейшее совершенствование МП возможно в направлении улучшения его точности за счёт объединения алгоритмов поиска путей в графе, а также перевод карт из 2D- в 3D-пространство.

Представленные результаты исследования могут быть использованы при разработке МП для поиска пешеходных маршрутов в других университетах и учреждениях.