Модальный анализ позиционной модели электрической системы

Режим электрической системы (ЭС) подвержен различного рода возмущениям: изменению нагрузки, генерации, состава оборудования, топологии сети и т.д. Поэтому при анализе, планировании и управлении режимами электрической системы важно точно оценить пределы по статической устойчивости. Под предельным по статической устойчивости понимают такой режим, в котором малое изменение его параметров в любом неблагоприятном направлении приводит к нарушению устойчивости.

При анализе статической устойчивости систем различают апериодическую и колебательную неустойчивость. Первый вид неустойчивости связан с появлением действительных положительных собственных значений матрицы линеаризованных дифференциальных уравнений, второй – с появлением комплексных собственных значений с положительной вещественной частью.

Для определения предела по статической колебательной устойчивости, как правило, применяется метод последовательного утяжеления. Начиная с устойчивого режима производится 5

изменение параметров режима и анализ собственных значений матрицы линеаризованных уравнений. Расчет предела по статической колебательной устойчивости требует значительных вычислительных и временных затрат, а также значительного объема исходной информации, который на практике недоступен. Данные о планируемом режиме работы и оперативная информация обычно ограничиваются составом и выработкой генерирующего оборудования и нагрузкой потребителей. Состав же включенного электрооборудования потребителей, как правило, неизвестен, а получение статических характеристик весьма проблематично. Возникновение колебательной неустойчивости в ЭС обусловлено чаще всего некорректным выбором настроек автоматических регуляторов. Поэтому при краткосрочном планировании и управлении режимами ЭС анализируют только статическую апериодическую устойчивость, полагая, что имеющиеся настройки автоматических устройств обеспечивают статическую колебательную устойчивость ЭС.

Широкое распространение в практике расчетов предельных по статической апериодической устойчивости режимов нашла модель с шинами неограниченной мощности [1]. Известно, что при выполнении определенных условий свободный член характеристического уравнения может изменить свой знак одновременно с матрицей Якоби уравнений установившегося режима (УУР), если анализ устойчивости ведется при следующих допущениях [2]: 1) активные сопротивления в цепях генераторов не учитываются; 2) отсутствуют демпферные обмотки и демпфирующие моменты; 3) все генераторы оснащены системами автоматического регулирования возбуждения (АРВ) с малыми постоянными времени и высоким коэффициентом усиления так, что модули напряжения поддерживаются неизменными; 4) неизменный механический момент на валу каждого генератора; 5) нагрузки задаются статическими характеристиками по напряжению; 6) один из генераторов имеет бесконечную постоянную инерцию и незначительные синхронные сопротивления, так что его угол и модуль напряжения поддерживаются неизменными. Поэтому в существующей практике расчетов предельных по статической апериодической устойчивости утяжеление режима проводится до тех пор, пока матрица Якоби УУР не станет вырожденной или не нарушится сходимость итерационного процесса.

Особенностью модели с шинами неограниченной мощности является зависимость предельных по статической апериодической устойчивости режимов от выбора балансирующего узла (БУ) [1]. Хотя для выбора балансирующего узла имеются определенные рекомендации, например в качестве балансирующего выбирать наиболее мощную генерирующую систему, либо наиболее мощную электростанцию. Однако такие рекомендации не могут во всех случаях гарантировать адекватный выбор БУ для определения действительного коэффициента запаса статической устойчивости.

Поэтому вызывает интерес вопрос определения предельного по статической апериодической устойчивости режима без явного назначения и использования балансирующего узла. В этом случае исследуемая модель будет в некоторой степени соответствовать так называемым позиционным моделям ЭС, когда учитываются только зависимости электромагнитных моментов синхронных машин от взаимного положения ЭДС генераторов.

Целью работы является исследование классической позиционной модели электрической системы, а также анализ ее предельного по статической апериодической устойчивости режима.

Анализ позиционной модели

Построение классических позиционных моделей связано с принятием упрощающих предположений, важнейшими из которых являются следующие [3]: 1) нагрузки при составлении схемы замещения ЭС представляются эквивалентными синхронными двигателями или (и) замещаются постоянными полными сопротивлениями; 2) все синхронные машины (СМ) - генераторы и двигатели - вводятся в схему замещения постоянными переходными ЭДС за расчетными индуктивными сопротивлениями, величины которых зависят от типа АРВ СМ; 3) все остальные элементы системы представляются пассивными схемами замещения, параметры которых не зависят от режима ЭС; 4) моменты первичных двигателей (приводимых механизмов) СМ считаются постоянными; демпфирование электромеханических колебаний генераторных (двигательных) агрегатов не учитывается.

Если в полученной таким образом расчетной модели сэквивалентировать пассивные элементы и принять малые отклонения частоты го » гоо , то систему линеаризованных дифферен- циальных уравнений движения роторов СМ можно представить в виде [4]:

где

д р 5

[ TJ ]

d 2 А5 dt ²

sap

А5 ,

'E k E m ( — G km sin( 5 k - 5 m ) + B km cos( 5 k - 5 m ) ) , k * m;

* E k Z E m ( G km sin( 5 k — 5 m ) - B km^k - 5 m ) ) , k = m; m e k

(1 а)

где [Tj ] - диагональная матрица постоянных времени инерции роторов турбины (приводного механизма) и генератора (двигателя), Ek, 5k - модуль и угол ЭДС СМ, величина которого дАР.                    „ _ „   _    „ „  , определяется типом АРВ; ----— производная небаланса мощности на валу k-й СМ по углу d5m

m; Gkm , Bkm - активная и реактивная проводимости между узлами k и m.

Матрица

д А р д5

является вырожденной. Согласно выражению (1 а) диагональные эле-

менты подматриц равны с обратным знаком сумме внедиагональных элементов строки. Для исключения вырожденности матрицы линеаризованных уравнений, уравнения возмущенного движения в абсолютных углах трансформируются в уравнения возмущенного движения в углах относительно угла одного из узлов (базисного), например, с номером b . Для этого из всех уравнений системы (1) вычитается уравнение узла b .

Рассмотрим матрицу линеаризованных уравнений (1), выделив базисный узел b :

Tg [ Agg ] Tg [Agb ] T- [ Abg ]  T- [ Abb ]

Для собственного значения¹ у матрицы A справедливо

det [ A - у ] = det

Tg [ Agg ] Y

Tb [ Abg ]

Tg [ Agb ]

Tb 1 [ Abb]-У

Матрица [ A ] вырождена, так как вырождена матрица линеаризованных уравнений (1). Если к последнему столбцу матрицы (2) прибавить все остальные столбцы, результатом будет нулевой столбец. Поскольку при прибавлении столбца к другому столбцу определитель матрицы не изменяется, то, применив такую процедуру к (3), можно получить

T g [ A gg ] ^{Y Y [} e ^]

Tb [ Abg ]

где все компоненты последнего столбца будут равны — у .

Поскольку при вычитании строки из других строк определитель также не изменится, то вычитание последней строки из вышележащих дает

Tg [Agg ]  [1] Tb  [Abg ]

Tb [ Abg ]

Раскрывая определитель (5) по последнему столбцу, можно получить det [ A — y ] = det

T g  [ A gg ]   ^{[ e ]} T b  [ A bg ] ^{Y [ 0 ]}

T ^{— 1} Г A. 1             -v

- y det

A ^e -y = 0 ,

где

A = T g [ A gg ] ^{— [ e ]} T b [ A bg ] .                         (6)

Но матрица A e

есть не что иное, как матрица линеаризованных уравнений возмущен- ного движения роторов синхронных машин в относительных углах. Следовательно, собственные значения этой матрицы будут в точности соответствовать собственным значениям исходной матрицы [A], т.е.

( T [ A gg ] — [ e ] T b ¹ Г A bg ] ) R = [ A e ] R e = Y R .                (7)

Рассмотрим, чему будут равны компоненты правых собственных векторов R ^e матрицы Ae" .

Воспользуемся соотношениями для правого собственного вектора исходной матрицы [ A ] :

T g Г A gg ] R g ^{+ T}g A gb^Rb   ^{y R}g ;                     ⁽⁸⁾

T b ¹ Г A bg ] R g + T b ¹ A bb R b = y R b .                       (9)

Из вырожденности матрицы [ A ] следует:

A gb ^=— [ A gg ] ^{[ e ]} ;

A bb =^— [ A bg ] ^{[ e ]} .

Подставляя эти выражения в (8)–(9), можно получить

Tg-1 Г Agg ][ Rg —[e] Rb ] = YRg;(10)

Tb—1 [ Abg ][ Rg —[ e ] Rb ] = yRb.(11)

Вычитание (11) из каждого уравнения (10) дает

Tg Agg —[ e] Tb Abg [Rg —[ e] Rb ] = Y [Rg —[ e] Rb ] .

Сравнение (12) с (7) обнаруживает, что

Re = Rg —[e]Rb .(13)

Выражение (13) показывает, что компоненты правых собственных векторов системы в относительных углах будут отличаться от соответствующих векторов исходной системы на одну и ту же величину, равную компоненте правого собственного вектора базисного узла.

Рассмотрим, чему будут равны компоненты левых собственных векторов системы (7) в

относительных углах. Для

TT левого собственного вектора [W]= Wg ,  Wb

справедливо сле-

дующее:

^Wg ^Tg [ A gg ] ^{+ W}b^Tb [ A bg ]   ^{y W}g

W ^T T^-1

Wg Tg

[ A gb ] + W b T b' l A bb ] = Y W b  ,

или

T

W _g ,

W b

T ^{- 1}

Tg

0    ^[ A gg ]  ^[ A gb ]

T -

¹ _ _^[ A bg ]    ^[ A bb ^] _

= Y W j , W b .

Умножая (15) справа на единичный вектор [ e ] , можно получить ° = Y ( W j [ e ] + W b ) ,

поскольку единичный вектор является правым собственным вектором, отвечающим нулевому собственному значению этой матрицы. Таким образом, при ненулевых значениях у :

W b =- W T [ e ] .

или

где

Подстановка (17) в (14) дает

^Wg ^{( T}g [ A gg ]^{- [ e ] T}b [ A bg ] ) = ^Wg

Когда у = ° , (15) примет вид

A e = у W j .

^Wg^Tg [ A gg ] + W b T b [ A bg ]   ⁰

W g t " [ A gb ]+ W b T b "¹ [ A bb ] = 0

В то же самое время для матрицы A^e

можно записать

.

W^{e T}

Ae

= ^We ^T ( T " ¹ [ A gg ]- [ e ] ^{T -} [ A

W eT T - [ A gg ] - W e T [ e ] ^Tb" ¹ [ A bg ] = W T ¹ [ A gg ] + W b^{T -} [ A bg ] = ° •

W b = - W ^{e T} [ e ] .

Умножая (21) справа на вектор [ e ] и учитывая свойства матрицы A e W eT T -¹ [ A gb ]+ W b j -¹ [ A bb ] = °.

, можно получить

Сравнение (21) и (23) с (19), а также рассмотрение (17) - (18) и (22) обнаруживают, что

левый собственный вектор W e матрицы A^e исходной матрицы [ A ] .

будет равен левому собственному вектору W_g

W e = w_g

и

W b =- w T [ e ] .                            (25)

Таким образом, собственные значения будут одними и теми же независимо от выбора базисного узла b и будут соответствовать собственным значениям полной системы дифференциальных уравнений возмущенного движения. Другими словами, если исходная система устойчива (неустойчива), то она будет устойчивой (неустойчивой) при любом базисном узле. Компоненты правых собственных векторов системы в относительных углах будут отличаться от соответствующих векторов исходной системы на одну и ту же величину, равную компоненте правого собственного вектора базисного узла. Компоненты левых собственных векторов всегда будут равны соответствующим компонентам левых собственных векторов полной системы.

Критерий предельных режимов позиционной модели

Проанализируем предельный по статической апериодической устойчивости режим позиционной модели, в котором матрица линеаризованных уравнений в относительных углах

A ^e имеет нулевое собственное значение у = 0 .

Представим матрицу A ^e

в виде

A ^e

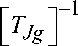
dA P g d^ _v

Г'Т 1 -1г "I ^dAPb

-[TJb ]  [e] "^b

"^

Умножим матрицу A ^e

ное выражение:

T слева на вектор-строку Wg , а затем транспонируем получен-

T g p g J Делая замену переменных

[ j J-1 w-

d- P b

^S5 g _

T

[ T Jb ]" 1 [ e ] T W g = 0 .

^X g  [ ^TJg J   W g ;

X p =- [ T Jb Г¹ [ e ] T W g ,

(27) можно представить в виде

T d- P g ^d5 g J

Xp +

d-Pb d^g

T

X b = 0.

В свою очередь, (28)–(29) дают:

X[TJb]+ 2 JX = 0.

V k * b

Поэтому, используя (28)–(31), критерий предельного по статической апериодической устойчивости режима позиционной модели ЭС можно представить в следующем виде:

SA P ”ss

T

a X = 0,

где a - вектор с компонентами ak = Tkk / 2TJ .                          (33)

m

Таким образом, критерий предельного по статической апериодической устойчивости режима классической позиционной модели соответствует критерию предельного по существованию установившегося режима ЭС с распределенным балансирующим узлом, в котором коэффициентами участия узлов в балансировке режима прямо пропорциональны их постоянным инерции СМ [5].

Проанализируем выражения (32)–(33). Левый собственный вектор матрицы Якоби (1), отвечающий нулевому собственному значению, определяет вектор нормали ^ к гиперповерхности мощностей, компоненты которого равны [5]:

^ m = ( 1 —дп / д P m ) % , (34) где дп / д P_m - относительный прирост потерь (ОПП).¹

Рассмотрение (32) - (34) позволяет выявить важную особенность позиционной модели.

Коэффициенты участия СМ a g в РБУ позиционной модели всегда положительны. Поэтому согласно (32) в ПР позиционной модели по крайней мере одна из компонент вектора нормали, например j , должна быть отрицательной. Но тогда согласно (34) это означает, что ОПП для СМ j в ПР больше единицы. Нагрузка энергосистемы в таком режиме получается меньше максимально возможной – снижение генерации в узлах с ОПП больше единицы приведет к увеличению полезно отдаваемой мощности. Другими словами, ПР позиционной модели находится дальше в пространстве напряжений, но ближе в пространстве мощностей. В теории и практике коэффициент запаса статической устойчивости ЭС обычно определяется в терминах мощностей. В этом случае позиционная модель будет давать заниженную оценку коэффициента запаса статической устойчивости.

Выводы

В работе была исследована классическая позиционная модель электрической системы. Исследования показали, что собственные значения позиционной модели будут одними и теми же независимо от выбора базисного узла и соответствуют собственным числам полной системы линеаризованных дифференциальных уравнений возмущенного движения в абсолютных углах. Компоненты правых собственных векторов системы в относительных углах будут отличаться от соответствующих векторов исходной системы на одну и ту же величину, равную компоненте правого собственного вектора базисного узла. Компоненты левых собственных векторов всегда будут равны соответствующим компонентам левых собственных векторов полной системы.

Исследование позиционной модели электрической системы обнаружило, что она неявно использует и реализует идеологию распределенного балансирующего узла и ее предельные по статической апериодической устойчивости режимы в точности соответствуют предельным режимам модели потокораспределения с распределенным балансирующем узлом, в котором коэффициенты участия узлов в балансировке активной мощности электрической системы назначаются пропорционально постоянным времени инерций синхронных машин. Поскольку постоянные времени инерции синхронных машин всегда положительные, а компоненты вектора нормали гиперповерхности мощностей взаимосвязаны через относительные приросты потерь активной мощности, в предельном режиме позиционной модели часть узлов имеют относительный прирост потерь активной мощности больше единицы. Нагрузка энергосистемы в этих предельных режимах получается меньше максимально возможной – снижение генерации в узлах с относительными приростами потерь больше единицы приводит к увеличению полезно отдаваемой мощности. Другими словами, предельный режим позиционной модели будет находиться дальше в пространстве напряжений, но ближе в пространстве мощностей, чем предельный режим модели с шинами неограниченной мощности. В этом случае позиционная модель будет давать заниженную оценку коэффициента запаса статической устойчивости.