Модель динамического распределения ресурсов

Рассматривается задача автоматического управления ограниченными аппаратными ресурсами c учетом ценности выделенных компьютерному приложению ресурсов (например, количества виртуальных машин, обеспечивающих работу приложения; объёма оперативной памяти и процессорного времени, предоставляемых виртуальным машинам или отдельным процессам) при текущей пользовательской нагрузке [1, 2]. Это позволит оптимально использовать ресурсы в процессе эксплуатации системы приложений, а именно, динамически добавлять или убирать количество любого ресурса во время работы с учетом потребностей и приоритетов каждого приложения системы и изменения пользовательской нагрузки на каждое приложение.

1.    Постановка задачи

Построим математическую модель рассматриваемой задачи для системы, состоящей из n приложений, использующих один первичный ресурс и m различных категорий вторичных (зависимых от первичного) ресурсов.

Пусть V ( t ), i = 1, . , n - количество первичного ресурса, обеспечивающего работу приложения i , в момент времени t . Обозначим через r i ( t ), i = 1, . , n , j = 1, . , m - количество ресурса j , выделенного приложению i в момент времени t . Ограничения на использование ресурсов записываются в виде:

v ( t ) e V ( t ), r i ( t ) e R ( t,V ( t ) ) , i = 1, _ , n,                               (1)

где V ( t ) , Rⁱ ( t , vⁱ ) – некоторые компактные множества.

Предполагается, что каждое компьютерное приложение имеет индивидуальный набор k i характеристик, которые однозначно описывают его текущее состояние с точки зрения пользователя (например, время отклика приложения, количество сетевых ошибок). Характеристика зависит от количества первичного ресурса, обеспечивающего работу приложения, объема вторичных ресурсов, предоставленных приложению и оказываемой на приложение с течением времени неуправляемой пользовательской нагрузки L (t), i = 1, ^, n . При этом характеристики могут быть составлены либо на испытательном стенде до запуска приложения в эксплуатацию, либо непосредственно в процессе работы приложения – в табличном виде. Обозначим через pi = pi (vi (t), ri 1(t), ri2(t),..., rim (t), L (t)), i = 1, ^, n, k = 1, ^, k1 - характеристику k приложения i , через pɶik (t) – целевой уровень соответствующей характеристики (желаемое значение характеристики, ниже которого она не должна опускаться во время эксплуатации компьютерного приложения). С помощью функций ki

^ ( t ) = Е “ ik p i ( v i ( t ), r i¹ ( t ), ™ , r im ( t ), L ( t ) )

k = 1

можно получить некоторую суммарную оценку характеристик каждого из приложений в момент времени t . Здесь через a _ik обозначены весовые коэффициенты, выбираемые согласно значимости каждой характеристики приложения. Будем называть функции t r i ( t ) уровнями сервиса приложений.

Задача состоит в поддержании значения уровня сервиса (2) не ниже некоторого целевого уровня (поддержание каждой характеристики не ниже ее целевого уровня) в моменты времени T = {t0,t0 + h, ™,t0 + qh = t1}. Данная задача равносильна минимизации отклонения уровня сервиса ki          q

V ' = Е a _ik Е max { 0, Р ik ( 1 ₀ + th ) - P i ( v i ( 1 ₀ + th ), r i ¹ ( 1 ₀ + th ), ™ , r im ( 1 ₀ + th ), L i ( t ₀ + th ) ) } k = 1       t = 0

для системы приложений в совокупности с учетом приоритета каждого из приложений. Обозначим через 5‘ ⁺ максимум 5* при всех допустимых значениях ресурсов (минимум R , очевидно, равен нулю).

Замечание. Для задачи поддержания характеристики не выше ее целевого уровня на T отклонение можно записать в виде

Е max { 0, - p^k ( 1 ₀ + th ) + p k ( v i ( 1 ₀ + th ), r i ¹ ( 1 ₀ + th ), ™ , r im ( 1 ₀ + th ), L ( 1 ₀ + th ) ) } ; t = 0

для задачи поддержания положительной характеристики как можно ближе к нулю на T отклонение можно записать так:

q

Е P i ( v ( 1 0 + th ), r i ¹ ( 1 0 + th ), ™ , r im ( 1 0 + th ), L ( 1 0 + th ) ) .

t = 0

Тогда исходную задачу динамического распределения ресурсов можно поставить в виде дискретной задачи оптимального управления следующего вида:

ki

У (t + h) = yi (t) + Е «ik max{0, pik (t) - pk (vi (t), ri1 (t), ™, rim (t), Li (t))}, k=1

t e T = [ 1 0 , t j,   / ( 1 0 ) = 0, i = 1, ™ , n ,

v ( t ) e V ( t ),    r i ( t ) e R i ( t , v ( t ) ) , i = 1, ™ , n ,

F(y(о)=E A-yS-) ^ min, i=1 V где yi (t) - сумма отклонений уровня сервиса приложения i к моменту времени t (т. е. в моменты времени 10,10 + h,™,t), через Pi обозначены весовые коэффициенты, выбираемые согласно приоритету каждого компьютерного приложения (большее значение весового коэффициента соответствует более высокому приоритету соответствующего приложения). Здесь роль управлений играют функции vi (t), ry(t), i = 1,™,n , j = 1,™,m .

Рассмотрим один из самых подходящих для дальнейшей практической реализации вариантов поставленной задачи (3), а именно, предположим, что на рассматриваемом промежутке времени управления постоянны, т. е. v i ( t ) = v i , r^ij ( t ) = r^ij , i = 1, ™ , n , j = 1, ™ , m . Тогда исходная задача может быть сформулирована в виде последовательности задач поиска минимума функции n • ( m + 1) переменных F ( У ( t ₁ j ) ) = G ( v ii , r Si ) при условиях (1), т.е.

F (У(t1 s)) = G(vi, rij) ^ min, v(t) e V(t), ri (t) e R (t, vi (t)), i = 1,™,n, v, r на множестве конечных временных отрезков T0 = [100, t10], где t10 = 100 + q0h0, T1 = [101, t11], где t11 = toi + q1 h1 и т. д.

Спецификой рассматриваемой задачи является зависимость вида динамической системы (3) от неизвестных функций L (t), i = 1,™, n. При этом предполагается, что известны значения этих функций в некоторые предшествующие рассматриваемому отрезку времени моменты 10s -lshs, 10s -(ls -1)hs, „., t0s - h'. Этот факт позволяет осуществлять прогноз изменения функций L (t) на рассматриваемом отрезке времени (например, с помощью численных методов аппроксимации функций одной переменной).

Полученное таким образом управление (количество выделяемых ресурсов) будет носить кусочнопостоянный характер:

V(t) = v, ri(t) = ri, te Ts = [t0s,t1 s], s = 0,1,.., что позволит легко реализовать его на практике в процессе эксплуатации системы приложений или использовать его в качестве начального управления в некоторой итерационной процедуре улучшения управления.

2.    Алгоритм решения задачи (на примере двух компьютерных приложений)

Рассмотрим алгоритм решения задачи динамического управления ресурсами на примере системы двух приложений – картографического сервиса «MapServer» и вычислительного сервиса «X-Com» [1].

Ресурсы, предоставленные приложениям: vⁱ ( t ) – количество виртуальных машин (ВМ), обеспечивающих работу приложения, r ^{i 1} – оперативная память ВМ (RAM, Мбайт), r ^{i 2} – доля физического процессора, предоставляемая ВМ (CAP, %). Ограничения на предоставление ресурсов записываются в виде:

V ( t ) >  1, n <  j^vi ( t ) <  v ⁺ , г ^- V ( t ) <  r i ( t ) <  r^{J +} v i (t ), i = 1

£ r i ( t ) <  ri ⁺ v ⁺ , r ^-<  r i ( t ) <  r ⁺ V ⁺ - ( n - 1) r^{j -} , i = 1, ^ , n , j = 1, ^ , m , i = 1

где n = 2, m = 2, r ^{1 -} = 128, r ^{1 +} = 512, r^{2 -} = 10, r^{2 +} = 100, v ⁺ = 3.

Для построения уровня сервиса первого приложения на дискретном наборе моментов времени {5,6,7,8,9} используются функции p11(v1,r11,r12,L1)   – среднее время отклика приложения, p12(v1, r11, r12,L1) – процент сетевых ошибок и L1(t) – пользовательская нагрузка на приложение, а также величина желаемого времени отклика p11 = 3000 миллисекунд. Функции p n( v 1, rn, r12, L) и p12(v1,r11,r12,L1) заданы таблично своим профилем производительности, функция L1(t) – значениями в моменты времени {0,1,2,3,4}. По этим данным были построены аппроксимации функциями p11, p12, L 1 по МНК в виде

{ _°                           1

• 0, X a ki ( v )( r ) ^{k h}( r ) ^{k 2} i ( L ) ^{k 3} i ^ ,

i=1                                                    J где aki – найденные согласно МНК постоянные действительные числа, а целые показатели степеней skli 3

удовлетворяют условиям - 2 <  s^ <  2, - 1 <  ^ s^ <  2;

i = 1

L1 (t) = b0 (L (0),^, L (4)) + b (L (0),^, L (4)) t, где b0 , b1 – найденные согласно МНК постоянные действительные числа.

Теперь отклонение уровня сервиса построим следующим образом: 44 1                              11       11    1    11    12    1                           12    1    11    12    1

д = X max { 0, - p + p ( v , r , r , L (5 + 1 ) ) } + ^ P ( v , r , r , L (5 + 1 ) ) . t = 0                                                                       t = 0

Можно подсчитать и максимальное отклонение уровня сервиса д ¹⁺ = 15070.

Для построения уровня сервиса второго приложения используется функция p ²¹ ( v ² , r ²¹ , r ²² ) – скорость расчета задач, находящихся в очереди, а также момент желаемого окончания расчетов 9 и величина начальной желаемой скорости расчета задач p ²¹ (0) = 18 задач/сек, что позволяет рассчитать текущую желаемую скорость расчета задач p ²¹ (5) = p ²¹ (0)( 9 - 5) задач/сек.

Функция p21(v2,r21,r22) задана таблично своим профилем производительности. По этим данным была построена аппроксимация функцией p 21 в виде p21 (v2, r21, r22) = 0.92451 - 0.00024r21 + 0.09777r22 - 0.345475v2 + 0.0002r21 v2.

Теперь отклонение уровня сервиса построим следующим образом:

S = ^ max { 0, p ²¹ (5) - p ²¹ ( v ²(5), r ²¹ (5), r ²² (5) )} .

t = 0

Можно подсчитать и максимальное отклонение уровня сервиса S ²⁺ = 90.

С учетом вышеизложенного, функцию G ( vⁱ , r^ij ) запишем в виде:

2 S vi ri1 ri2 1 2 11 12 21 22                           ,,

G(v,v,r ,r ,r ,r )= >,в-----—-->min,(4)

i=1

где Д = в ₂ = 1 (это означает равные приоритеты обоих приложений).

Написана программа, моделирующая работу системы двух указанных приложений при задаваемой случайным образом пользовательской нагрузке с применением описанного метода выбора ресурсов. Ниже приводится пошаговое описание работы программы.

Шаг 1. Полагается s = 1, t _{0 s} = 5 мин.

Шаг 2. Снимаются показания пользовательской нагрузки L(t) в моменты t0s - 5, t0s - 4, t0s - 3, t0s - 2, t0s -1. Производится расчет прогноза изменения пользовательской нагрузки по МНК в виде L *( t)=b0 + b1t.

Шаг 3. Решается задача условной минимизации (4)

*   *                      1   2   11   12   21   22

G ( v , r ) = min G ( v , v , r , r , r , r ) , ( v , r ) € W

W = <  ( v , r )

vi > 1, 2 < v1 + v2 < v+, r1 - < ri (t) < rJ+v+ - r1 -, r11 + r21 < rj+v+, r1 vi (t) < r1 (t) < r1+vi (t), i, j = 1,2

методом покоординатного спуска с постоянным шагом, в качестве начального приближения выбирается случайным образом набор точек в допустимой области.

Шаг 4. Перераспределяются ресурсы приложениям согласно найденным значениям ресурсов ( v * , r * ) .

Пересчитывается

^ p

21                          21   2*   21*   22*

Р ⁽ t 0 s ⁾⁽ ^ ^- t 0 s ) ^{- 5} Р ^{( v} , ^r , ^r )

целевой уровень второго

приложения по формуле

9 - t0 s - 5

. Полагается s = s + 1, 1 _{0 s} = 1 _{0 s} + 5. Осуществляется переход к ша-

гу 2.

3.    Вычислительные эксперименты

Для проведения тестовых расчетов был сгенерирован случайный набор гладких пользовательских нагрузок. Две из них показаны на рис. 1 (первый вариант пользовательской нагрузки представлен сплошной линией, второй – пунктирной).

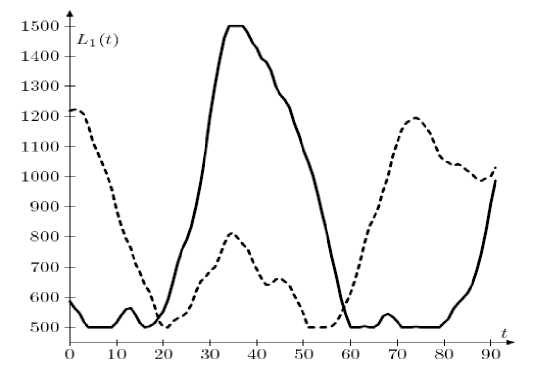
Рис.1

Результаты работы программы при v+ = 3 (не более трех ВМ на оба приложения в сумме) и увеличивающемся приоритете второго приложения (в зависимости от роста целевого уровня сервиса – желаемой скорости расчета задач) для каждого из вариантов прогноза представлены на рис. 2, 3 (рис. 2 соответствует первому варианту пользовательской нагрузки, рис. 3 – второму). Изменяющийся во времени целевой уровень второго приложения имеет смысл ограниченного конечного времени расчета. Из рисунков видно, что при различных пользовательских нагрузках алгоритм дает устойчиво хорошее динамическое перераспределение ресурсов с учетом поддержания изменяющихся характеристик на целевом уровне.

Заключение

Представленная математическая модель задачи распределения ресурсов для системы компьютерных приложений построена с использованием теории оптимального управления, при этом в качестве управления рассматривается количество ресурсов, выделяемых каждому компьютерному приложению. Предложенный метод решения задачи учитывает потребности и приоритеты каждого из приложений при изменяющейся пользовательской нагрузке на приложения, что позволяет существенно повысить эффективность совместного использования ограниченных ресурсов системы.