Модель динамической системы промышленного трактора для исследования вибрационной нагруженности рабочего места водителя-оператора

При создании новых и модернизации существующих моделей мобильной дорожностроительной техники обязательным условием является выполнение требований санитарных норм на рабочем месте оператора-водителя. На общий уровень комфорта на рабочем месте существенное влияние оказывает вибрационная нагруженность. Известно, что повышенный уровень вибраций не только способствует снижению производительности труда и быстрой утомляемости водителей, но и приводит к развитию целого ряда профессиональных болезней, в частности, заболеваниям суставов, позвоночника, вибрационной болезни и других [1].

Для оценки вибрационной нагруженности рабочего места водителя-оператора при проектировании новых машин и для обоснованного выбора параметров системы виброизоляции рабочего места в настоящее время широко применяется математическое моделирование. Расчетные исследования вибрационной нагруженности включают следующие этапы:

– формирование в случайного внешнего воздействия на динамическую систему машины;

• –    математическое моделирование движения машины, получение функции спектральной плотности виброускорений на месте водителя;

• –    расчет средних квадратических значений виброускорений в стандартных октавных или третьоктавных полосах;

• –    сопоставление полученных значений с предельными значениями из санитарных норм [2]. В случае превышения предельных значений производится корректировка параметров системы виброизоляции.

Моделированию динамики гусеничных машин различного назначения посвящены многочисленные работы отечественных и зарубежных ученых. Обобщенные данные по моделированию динамики машин с подвесками различных типов представлены в [3]. Машины с индивидуальными упругими подвесками рассмотрены, например, в [4]. В работах [5, 6] предложены математические модели, описывающие машины с балансирной упругой подвеской. В качестве источников вибрации обычно рассматриваются силовая установка, рабочие органы и ходовая система машины. При этом вклад каждого из источников вибрации зависит от особенностей конструкции машины. В работе [7] на основании результатов экспериментальных исследований показано, что для техники на базе промышленного гусеничного трактора с полужесткой подвеской в низкочастотной области (до 10 Гц) основным источником вибрации является движитель машины. В связи с особенностью конструкции ходовой системы (шарнирное соединение гусеничных тележек с рамой трактора) вибрации, возникающие при работе движителя, практически без ослабления передаются на корпус трактора. При этом для выполнения требований санитарных норм по вибрациям необходимо использовать специальное виброзащитное сиденье.

Данная статья посвящена моделированию динамики промышленного трактора с полужест-кой подвеской. Математическая модель, описывающая такую машину, была предложена Д.В. Хрипуновым [7], а затем развита в работах В.К. Халтурина [8] и Ю.О. Прониной [9]. Модель описывает вертикальные и продольно-угловые колебания корпуса машины, вызванные движением опорных катков по гусеничной ленте, находящейся на податливом грунте. Очевидно, что для получения адекватных результатов подобная модель должна достаточно подробно отображать особенности геометрии опорной поверхности траков, упругопластические свойства грунта и ряд других особенностей. Однако в моделях [7–9] грунт рассматривается как упругое основание, не учитывается наличие грунтозацепов на опорной поверхности траков; для описания виброзащит-ного сиденья с водителем используется простейшая одномассовая модель. В связи с отмеченными особенностями результаты моделирования являются достаточно приближенными.

Для снижения уровня вибраций на месте водителя до предельно-допустимого уровня используется виброизоляция кабины, а также виброзащитное сиденье. Гусеничные тележки, корпус машины, кабина, виброзащитное сиденье и тело водителя образуют единую динамическую систему. В связи с этим для получения наиболее точных расчетных оценок необходимо использовать единую математическую модель, описывающую динамику такой системы.

В данной статье представлена математическая модель, описывающая динамику системы «гусеничная тележка – корпус – кабина – виброзащитное сиденье с водителем» гусеничного трактора с полужесткой подвеской. Модель отличается подробным описанием гусеничной тележки трактора и использованием многомассовой модели подсистемы «виброзащитное сиденье – водитель». Расчетные исследования выполнены на примере трактора производства Челябинского тракторного завода с 5-катковой гусеничной тележкой (соответствующие модификации Т-130, Т-170 и более поздних моделей). Рассматривается трактор, оснащенный виброзащитным сиденьем Sibeco.

Материалы и методы

В настоящее время для исследования динамики широкое применение находят специализированные пакеты программ (ADAMS, ANSYS Motion, Универсальный механизм и др.). Использование подобных пакетов позволяет создать весьма подробную модель, однако расчеты с помощью такой модели требуют применения мощных компьютеров и занимают много времени. В [10] предложена модель, в которой динамическая система трактора разделена на две подсистемы: гусеничную тележку и корпус трактора с кабиной. Для создания модели тележки использован пакет программ ANSYS Motion [11]. Модель тележки достаточно подробная, она включает гусеничную ленту, состоящую из соединенных между собой траков, балку с опорными и поддержи- вающими катками, ведущее и направляющее колесо. Грунт моделируется нелинейной вязкоупругой средой. При создании модели принято допущение, что динамические нагрузки, возникающие при движении трактора, существенно меньше статических. В связи с этим в пакете программ ANSYS Motion моделируется движение одной тележки, нагруженной статическим весом половины трактора. Расчет соответствует ограниченному времени движения с постоянной скоростью. В результате расчета получают процессы изменения вертикального перемещения оси ведущего колеса (ZT) и угловых перемещений тележки (ϕT). В дальнейшем эти процессы используются как процессы кинематического нагружения для математической модели, включающей корпус трактора, кабину и виброзащитное сиденье с водителем. Модель тележки подробно описана в работе [10]. Там же представлены результаты расчетных исследований влияния свойств грунта, расстановки опорных катков и других факторов на колебания тележки.

При разработке второй части математической модели, включающей корпус трактора, кабину и виброзащитное сиденье с водителем, приняты следующие допущения:

• –    предполагается, что колебания гусеничных тележек происходят синхронно и синфазно, поперечные колебания корпуса не учитываются;

• –    в качестве внешнего кинематического возбуждения рассматриваются процессы изменения вертикального перемещения оси ведущего колеса ( Z T ) и угловых перемещений тележки ( ϕ T ) при движении трактора по податливому грунту на ровном участке трассы;

• –    при моделировании динамики виброзащитного сиденья с водителем рассматриваются вертикальные колебания.

Расчетная схема этой части математической модели представлена на рис. 1, a. Она включает тележку (1), корпус (2) и кабину (3); виброзащитное сиденье с оператором (4) показано условно. Обобщенными координатами являются угол поворота корпуса ( ϕ КОР ), вертикальные и угловые перемещения кабины ( ϕ К , Z К ). Элементы системы имеют массы m 12 , m 13 и моменты инерции I 12 , I ₁₃ относительно точек О₁, О₃ соответственно.

Для моделирования виброзащитного сиденья с водителем могут быть использованы расчетные схемы различной сложности. В наиболее простых моделях рассматривается одномассовая механическая система. Однако, как показывают результаты исследований ряда авторов, для адекватного описания колебаний тела водителя-оператора необходимо использовать многомассовую динамическую модель. В частности, в работах [12, 13] представлены двух- и трехмассовые модели. Трехмассовую модель также предлагается использовать в стандарте ISO 5982.2001 [14]. Использование подобных моделей позволяет получить более точную оценку вибрационной нагру-женности рабочего места водителя, исследовать колебания различных частей тела, а также использовать новые критерии вибрационной нагруженности, например, количество поглощенной энергии колебаний.

В предлагаемой математической модели для описания виброзащитного сиденья с водителем предложено использовать 4-массовую модель [15, 16], описывающую тело водителя, объединенную с моделью виброзащитного сиденья (рис. 1, b).

Упругий элемент c ₁, а также элементы вязкого трения b , b ₁ описывают систему подрессори-вания сиденья, m ₁ – основание подушки сиденья, c ₂, b ₂ – подушку сиденья. Элементы m ₂ – m ₅ , c ₃ – c 5 , b 3 – b 5 описывают тело водителя-оператора. Обобщенными координатами этой части модели являются вертикальные перемещения y ₀… y ₅. В связи с тем, что при движении трактора вибрации, вызванные работой гусеничного движителя, имеют небольшую амплитуду, жесткости и коэффициенты вязкого трения элементов модели при дальнейших расчетах принимались постоянными, но зависящими от массы водителя-оператора и настроек сиденья. На предыдущем этапе исследований была проведена серия статических и динамических испытаний сиденья, а также динамических испытаний сиденья с находившимися на нем испытателями [17]. По результатам испытаний определены параметры модели для испытателей различной массы, а также подтверждена адекватность предлагаемой модели.

Для вывода уравнений движения рассматриваемой динамической системы использованы уравнения Лагранжа второго рода [18]. В результате получена следующая система дифференциальных уравнений:

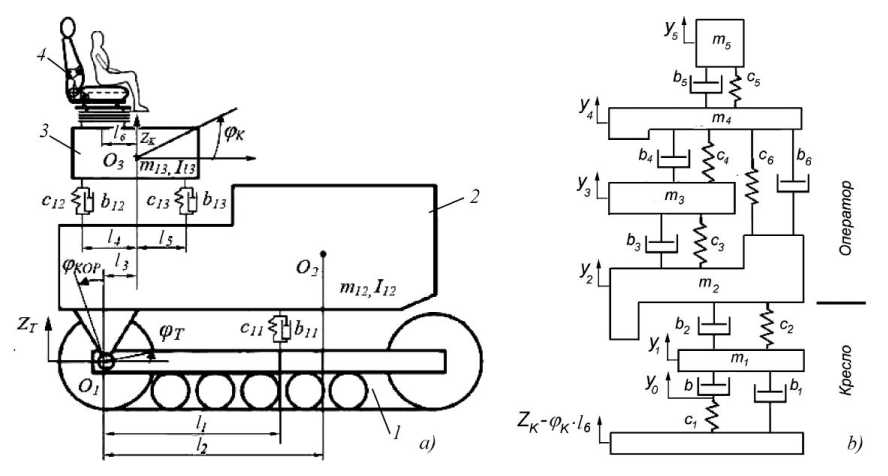
Рис. 1. Расчетная схема модели промышленного трактора: а – гусеничная тележка, подрессоренный корпус, кабина; b – виброзащитное сиденье с водителем

Fig. 1. Calculation scheme of the industrial tractor model: a – tracked bogie, sprung body, cabin; b – vibration-protective seat with driver

^ф KOP ( I 12 ⁺ m 12 l 22 ) ⁺ ^ КОР l 21 ^C 11 ^{+ (} l 4 ^{+   l}3 ) c 12 ^{+ ( l}3 ^{+ l} 5 ) c 13

⁺ zk [ ^c 12 ⁽ l 4 - ¹3 ^{)- c} 13 ^{( l}3 ^{+ 1} 5 ) ] ⁺

^{+ ф} K [ ^c 12 ⁽ l 4   ^l3 ) l 4   ^c 13 ^{( l}3 ^{+ 1}5 ) ^l5 ] ⁺ Ф кОР ^l 12 b 11 ^{+ (} l 4

- ¹3 ) b 12 ⁺ b 13 ^{( l}3 ^{+ l}5 )

+

⁺ z k [ ^b 12 ⁽ l 4 - ¹3 ^{)- b}13 ^{( l}3 ^{+ l}5 ) ] ^{+ ф} к [ ^b 12 ⁽ l 4 - ^l3 ) l 4 - ^b 13 ^{( l}3 ^{+ l}5 ) ^l5 ] =

• = ^zT [ ^l 1 ^c 11 ^{+ c} 12 ⁽ l 4 - ¹ 3 ) - ^c 13 ^{( l} 3 ^{+ l}5 ) ]+ ^ф T^c1111 ^{+ z}T [ lb 11 ^{+ b}12 ⁽ l 4 - ¹3 ^{)- b} 13 ^{( l}3 ^{+ 1}5 ) ] ^{+ ф} T^b1 1 ^l 12 - ^m 12 l 2 ^z T

• ^m13^zK ^{+ z}K ^{( c} 12 ^{+ c} 13 ^{+ c} 1 ^{) + ф} K [ ^c 13 ¹5 - ^c 12 l 4 - ^c 1 l 6 ^{] + ф} КОР [ ^c 12 ⁽ l 4 - ^l3 ) - ^c 13 ^{( l}3 ^{+ l}5 ) ] ^-

• - y 0 ^c 1 ^{+ z}K ( ^b12 ^{+ b}13 ^{+ b} 1 ^{) + ф} К [ ^{( b} 13 ¹5 - ^b 12 l 4 - ^b 1 l 6 ) ] ^{+ ф} КОР [ ^b 12 ⁽ l 4 - l 3 ^{) - b} 13 ⁽ l 3 ^{+ l}5 ) ] ^{- b} 1 ^y 1 =   ⁽¹⁾

= ^zT ( ^c 12 ^{+ c} 13 ) ^{+ z}T ( ^b 12 ^{+ b} 13 ) ,

I 13 ^ф K ^{+ z}K ^{(- c} 12 l 4 ^{+ c} 13 ¹5 ^{- c} 1 ¹ 6 ^{) + ф} K ( ^c 12 l 4 ^{+ c} 13 ¹ 5 ^{+ c} 1 ¹6 ) ^{+ ф} KOP [ ^{- c} 12 ¹ 4 ⁽ l 4 ^{- 1} 3 ^{)- c} 13 ¹5 ^{( l} 3 ^{+ 1}5 ) ] ⁺

• ⁺ y 0 ^c 1 ^l6 ⁺ Z K ( b 12 l 4 ^{+ b} 13 ¹5 - ^b 1 ¹6 ^{) + ф} K [ b 12 l 42 ^{+ b} 13 ^l 52 ^{+ b} 1 ¹ 62 ] ⁺ Ф KOP [ ^{- b} 12 ¹ 4 ( ^l 4 - l 3 ^{)- b} 13 ¹5 ( l 3 ^{+ 1} 5 ) ] ^{+ + y} 1 ^b 1 ¹ 6 = ^zT ^{( c} 13 ¹5 ^{- c} 12 ¹ 4 ) ^{+ z}T ^{( b}13¹ 5 ^{- b} 12 ¹ 4 ) ,

• b (y0 -y1 ) = c1 (zK -ФKl6 -У0 )  m1 y1 = b (У0 -У1 ) + b (zK -фKl6 -У0 ) + c2 (У2 -У1 ) + b2 (y2 -y1

,, m2 y2 = c2 (У1 - У2 ) + b2 (y1 - y2 ) + c3 (У3 - У2 ) + b3 (y3 - y2 ) + c6 (У4 - У2 ) + b6 (y4 - y2)

m 3 ^У 3 = ^c 3 ( У 2 ^- У 3 ) ^{+ b} 3 ( ^У2 ^{- У} 3 ) ^{+ c} 4 ( У 4 ^- У 3 ) ^{+ b} 4 ( ^У 4 ^{- У} 3 ) ,

• m4У4 = c4 (У3 - У4 ) + b4 (У3 - У4 ) + c5 (У5 - У4 ) + b5 (У5 - У4 ) + c6 (У2 - У4 ) + b6 (У2 - У4

• ^m 5 У 5 = ^c 5 ( У 4 ^- У 5 ) ^{+ b} 5 ( ^У 4 ^{- У} 5 ) •

Для решения задачи статистической динамики в данной работе использован спектральный метод. Функции спектральной плотности виброускорений элементов динамической системы получают из функций спектральной плотности внешнего воздействия с помощью частотных передаточных функций [19]. При моделировании движения тележки в пакете ANSYS Motion ее скорость задается постоянной. Получаемые в результате процессы изменения во времени вертикальных и угловых перемещений ZT(t) и фT(t) являются периодическими с периодом, равным времени прохождения опорным катком одного трака гусеницы. Если скорость движения варьи- руется в соответствии со случайными изменениями сил сопротивления движению, эти процессы становятся узкополосными случайными коррелированными процессами. В результате их обработки получают функции спектральной плотности Sz(f), Sv(f), а также функции взаимной спектральной плотности S^z(f, Szy (f [20]. На рис. 2 представлены графики этих функций для случая движения трактора по грунту средней жесткости (суглинок) на первой передаче с изменяющейся скоростью.

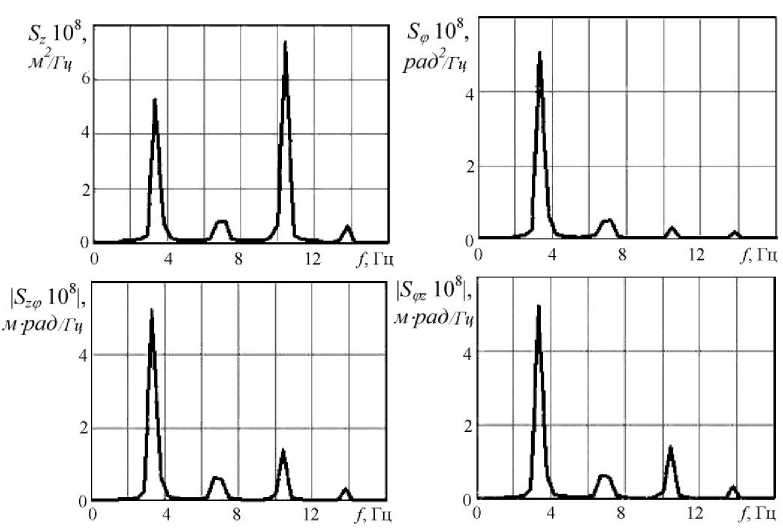
Рис. 2. Функции спектральной плотности внешнего воздействия

Fig. 2. Functions of spectral density of external influence

Полученные спектральные плотности внешнего воздействия и передаточные функции в дальнейшем используются для расчета функции спектральной плотности виброускорений на месте водителя, а также средних квадратических значений виброускорений в стандартных октавных или третьоктавных частотных полосах.

Результаты и обсуждение

Модули передаточных функций от Z _T и ф Т к координате x (перемещение пола кабины) W _{x/ y T} , W _x/ZT представлены на рис. 3. Там же приведены модули передаточных функций от внешнего воздействия к обобщенным координатам модели сиденья с водителем (y ₂... y ₅ ; W _{Yi/ y T} , W _Yi/ZT ) для водителя массой 73 кг.

На передаточных функциях имеется два максимума: вблизи частоты 2 Гц, соответствующий собственной частоте системы с преобладанием угловых колебаний корпуса, а также вблизи 10,5 Гц, соответствующий собственной частоте системы с преобладанием вертикальных колебаний кабины.

В отечественной нормативной литературе приводятся предельные значения средних квадратических значений виброускорений на подушке сиденья водителя. Их расчетная оценка в простейшем случае может быть получена с использованием одномассовай математической модели, описывающей виброзащитное сиденье с водителем. Для оценки влияния структуры модели на получаемые расчетные оценки передаточные функции от внешнего воздействия Z _T и ф Т к перемещению массы на подушке сиденья y ₂ W _{Y2/ y T} , W _Y2/ZT были получены для двух вариантов модели: полной, с использованием многомассовой модели тела водителя (см. рис. 1, b), и упрощенной одномассовой, когда элементы m 2 - т ₅ заменялись одной массой. Соответствующие результаты представлены на рис. 3 (1 - расчет с использованием полной модели, 2 - с использованием упрощенной модели). Анализ этих данных показывает, что максимальные различия (на частотах вблизи 10 Гц) превышают 25 %.

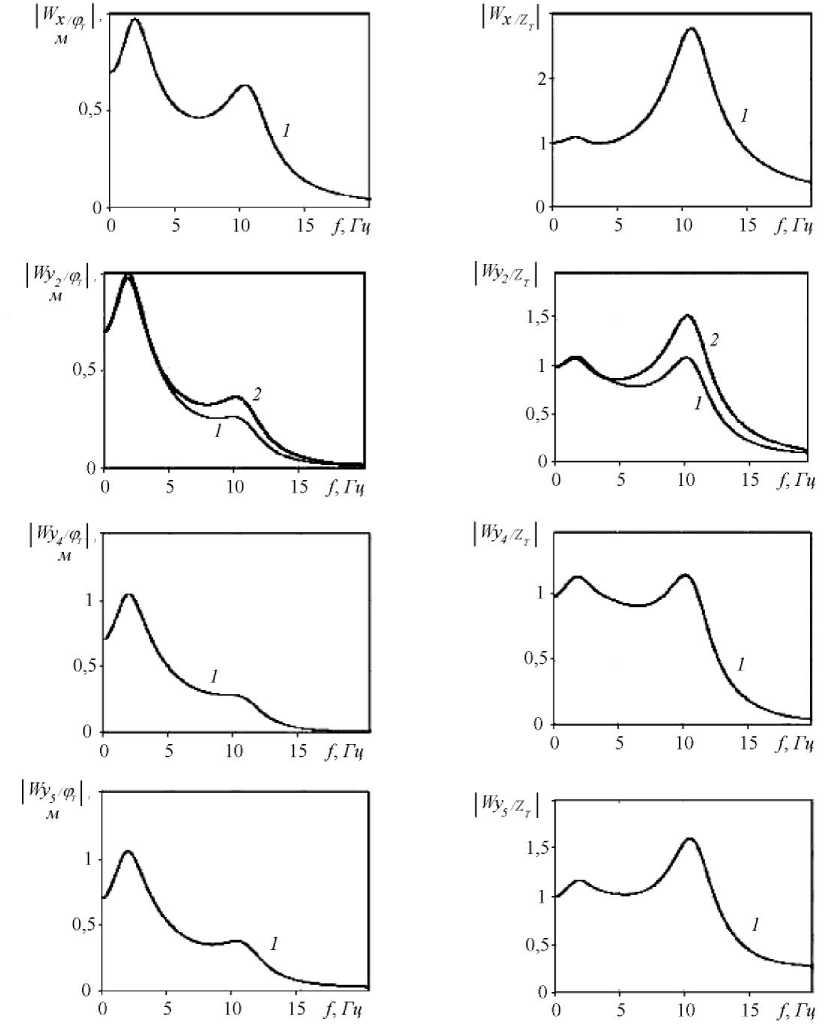
Рис. 3. Частотные передаточные функции динамической системы:

1 – расчет с использованием полной модели, 2 – с использованием упрощенной модели

Fig. 3. Frequency transfer functions of a dynamic system:

1 – calculation using the full model, 2 – using the simplified model

Заключение

В статье представлена математическая модель динамической системы промышленного гусеничного трактора с полужесткой подвеской, описывающая низкочастотные колебания, вызванные движением опорных катков по звенчатой гусенице. Представлены дифференциальные уравнения движения и методика расчета значений передаточных функций, а также расчета функции спектральной плотности виброускорений на месте водителя. Показано, что для получения наиболее точных оценок необходимо использовать многомассовую модель, описывающую виброза-щитное сиденье с водителем. При этом появляется дополнительная возможность исследовать ко- лебания различных частей тела оператора, а также использовать новые критерии вибрационной нагруженности, например, величину поглощенной энергии.

Разработанная математическая модель и методика были использованы в ряде расчетных исследований, результаты которых будут представлены в последующих публикациях.