Модель движения автомобилей на участках дорог с ограниченной видимостью

К настоящему времени нет достаточно надежных методов расчета допускаемых скоростей движения для участков с необеспеченной видимостью. Существующие теоретические расчеты скоростей движения на участках горизонтальных и вертикальных кривых разработаны для нужд конструирования и расчета автомобилей и не могут быть использованы для нормирования.

Кроме того, входящие в формулы расчета скоростей значения коэффициента сцепления определены при полной блокировке колеса, что не соответствует действительным условиям торможения из условия устойчивости автомобиля в пределах полосы движения.

Чистяков А.Г. , Чернышева Е.В., 2014

Допустимую скорость движения на участке с криволинейной траекторией будем выбирать, исходя из требования остановки автомобиля в пределах зоны видимости без потери устойчивости. При расчете примем сле- дующие допущения:

• 1.    В процессе торможения движение

• 2.    Величина угловой скорости поворота

• 3.    Водитель осуществляет торможение таким образом, что полностью используются тормозные свойства наименее нагруженного колеса.

• 4.    Коэффициент сопротивления уводу шин

• 5.    Сопротивление качению мало.

остается управляемым, водитель удерживает автомобиль в пределах полосы движения. Будем считать, что радиус поворота на всем участке торможения остается постоянным.

управляемых колес мала.

мало зависит от изменения нагрузок на шину.

Из теории автомобиля известно [1,2], что при криволинейном движении ускорение центра тяжести автомобиля может быть найдено по выражению:

v2 b dv , v d0 j =— +--+ b--, y R R dt L dt dv v2

j =-- b----

^J x dt _R 2 ’

В

этих выражениях — > 0, если проис-dt ходит ускоренное движение автомобиля.

При криволинейном движении автомобиля под действием поперечной силы кузов автомобиля поворачивается относительно оси крена на угол ^ . Угол крена кузова может быть найден из выражений:

M jh п7у у ,

I С + С I-M gh k у1 у2 J п5 у

где Мп - подрессоренная масса; h ^ - плечо крена (расстояние от центра тяжести подрессоренной массы до оси крена); С^ , С ^ - уг ловые жесткости передней и задней подвески.

При приближенных расчетах в знаменателе выражения (5) можно не учитывать второе слагаемое. Тогда угол крена определится по выражению:

У =

M jh п7 у у

С  + С у1 у 2

Вследствие крена кузова реакции на внутренних колесах уменьшается, а на внешних возрастает на величину A R z :

где j , j xy

- соответственно ускорения, действу-

ющие в поперечной и продольном направлениях; v - мгновенная скорость автомобиля; R - радиус поворота; L - база автомобиля; b - расстояние от центра тяжести до оси заднего моста; 0 - угол

с у       Cw

у

AR  =--—, AR „ = z 1     B1   ,    z 2     B 2

где By, B^ - колеи переднего и заднего мостов автомобиля соответственно.

поворота управляемых колес.

Поперечные реакции, действующие на передний и задний мосты автомобиля, определяются из выражения:

Подставляя (6) в (7) имеем:

AR z1

Су1   М j"у,

С + С     п УБ, у1    у 2

M у 1 = "t

b 2 v

R

b ² + р ² dv

+-------+

R dt

v А 2 dOdO + — I b ² + р ² I — . L k ) dt

AR z2

Су2

2 _М

С + С     - у1   у 2

j "у пyB

M ^a y ² = L

a 2 v

R

ab - р ² dv +------

R dt

Нормальные колесах:

реакции на внутренних

R

v

+ —

L

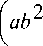
P

d9

dt

R

"

z ₁

z ₁

-AR  , z1

где M a - масса автомобиля; a - расстояние от центра тяжести до оси переднего моста; р - радиус инерции автомобиля относительно вертикальной оси, проходящей через центр тяжести.

R

"

z ₂

R z ₂

-AR z2

Реакции R z^ и R z₂ определяются по

выражениям:

где

где

R z1

R z ₂

= M

a

= M

a

gb ⁺ jxhg

L ga — jxhg ’

L

h _g - высота центра тяжести автомобиля.

M

R- = —aI gb + j h I — zl    2L V xx g7

—

h a m j ^—- .

^{1 п j}y b^

R

—

M a

2 L

a M j

2 п y

C^-\ a =------- ¹ C + C - 1     - - 2

C

a 2 =

^- 2

C + C

^-1   ^- 2

V ga ^— jxhgу

Замедление автомобиля связано с тормозной силой соотношением:

—

dv

— = M

—

dt      ^a

1P т.

Тогда ускорение, направленное вдоль оси автомобиля j _x , исходя из (2) определится выражением:

jx

—

M —

.           2 I

¹ Р + b— M

^{a т} »2

V           R 7

_a .    (14)

^h -

B ₂

Знак (-) указывает, что сила P направлена в сторону, противоположную движению v ² автомобиля, обычно слагаемое b    значи-

R ²

тельно меньше продольного ускорения. Поэтому при приближенных расчетах можно принять:

Р = j M . т x a ^.

Продольная составляющая горизонтальной реакции дороги внутреннего колеса, которая может быть использована для торможения, находится из соотношений:

В данном выражении знак силы принят положительным, так как направление силы учтено в формулах, определяющих перераспределение нормальных реакций при торможении [4]. Из формул (12) и (15) имеем:

-RZ, -^(y, )2 +[^J .

Р"

т

- RZ ₂ =^⁽ y 2 ) ² +[ PT₂ ) .

jM xa

.

21+/Т

V ^т 7

Если коэффициент сцепления на дороге

меньше расчетного по оптимальному тормо-

жению, то ограничение интенсивности тормо-

жения происходит по опасности потери управляемости автомобиля вследствие юза передних колес [3]. Рассмотрим процесс торможения в этом случае. Суммарная тормозная сила, развиваемая автомобилем в этом случае, будет:

Если принять условие, что отношение продольной и поперечной составляющих у внутреннего переднего колеса определяется из

У- выражения у^ = -У-, то из (11) и (16) получим Pт уравнение для нахождения допустимого замедления автомобиля:

R"

z ₁

jM 1 _x

^ 1

a

Р = Р т

т

+ Р = 2 Р"

тт

z

2 Р" т ₁

1+1

2 Р" т

+---— =

1   вт т , (12)

21+IT

V ^т 7

Или, используя выражение (9), имеем:

в

V Тщ 7

M

—— I gb + j h

2 L V x^x g

—

где в - коэффициент распределения тормоз

—

Р

ной силы: в_т

т ₁

j  Mj

a m j ^- = — x i п x b^    ф

Р

т ₂

2[‘+/Т

V ^т 7

После преобразований получим:

jx

[ Mh

= 2 а —п j—

¹ М y В_л

V      а1

gb

2 L

А —1

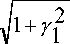
L

Ф

[1+1 'I 1+

V    т У/

Аналогичным образом, если принять условие, что ограничение тормозной силы происходит по блокировке колес заднего мо- ста, получим:

Р = Р + Р тт т

= 2 Р" т ₂

Р т ₂

+ 2В Р"   = 2Р”  (1 + в ), тт   т   т j M        Yэ x a j =2_

= 2^ • ² p ;₂ ■

R"

z ₂

jM xa

—7--- \ J1 + Y 2 .

24 ( 1 + Р_т ) ⁴    '^

М [

—а I ga - J_v h„ 2 L V     xz g

—

а м

п

h

x

B z

jM x

,

2 ф

jx z

a

- ^{Y 2}

= ² 2 L “ “

V

M п _j

М ^x а

h

V

В

x

z 7

h

A—1

. (19)

x

V

g + l' Y2

L 1 + вт ф у

В выражениях замедления обозначение показывает, что расчет проводится с учетом зависимости сцепления от скорости, а именно:

Ф = ф (1 + Av I, 7 v o oV о,

где ф - коэффициент сцепления, замерный при малой скорости; А - коэффициент, зависящий от состояния покрытия, типа шины и скорости движения (А=0,015-0,03).

Если коэффициент сцепления на дороге меньше расчетного по оптимальному торможению, то ограничение интенсивности торможения происходит по опасности потери управляемости автомобиля вследствие юза передних колес. В этом случае допустимое замедление автомобиля находится по формуле (18).

Если коэффициент сцепления на дороге больше расчетного по оптимальному торможению, то ограничение тормозной силы происходит по блокировке колес заднего моста. Допустимое замедление в этом случае определяют по формуле (19). Двойным интегрированием формулы (18) или (19) определяется тормозной путь автомобиля S _т [3-5].

Полный остановочный путь автомобиля S складывается из пути, проходимого авто-т о мобилем за время реакции S , и тормозного пути S :

S T  = So ⁺ S T .

o

Длина пути зависит от начальной скорости автомобиля v , продолжительности реакции водителя t , времени срабатывания привода t и времени нарастания замедления t .

np                                       з

Таким образом:

So

t + 1 p np

V t3

+ —

^vo .       (²²)

Сопоставляя полный остановочный путь с имеющейся зоной видимости, определяется допустимая скорость движения.

Авторами выполнен расчет допускаемой скорости движения автомобиля для участков горизонтальных и вертикальных кривых на лесных автомобильных дорогах с использованием тормозных свойств наименее нагруженных колес. А также изучены нормальные реакции на колесах автомобиля при его торможении. Представленная методика расчета допускаемой скорости является наиболее надежной для участков с необеспеченной видимостью.