Модель движения крови в артериальном сосуде во время систолы и анализ напряженного состояния стенки с учетом винтовой анизотропии

В работах [9, 11] содержатся обзоры публикаций, в которых рассматриваются различные математические модели, предназначенные для описания гидродинамики кровообращения в крупных артериальных сосудах. Значительное внимание в этих обзорах уделено описанию модели, в которой стенка артериального сосуда рассматривается как ортотропная цилиндрическая оболочка (безмоментная теория), а кровь – как вязкая жидкость, движение которой описывается линейными уравнениями Навье–Стокса. В рамках этих моделей движение частиц крови является поступательным вдоль оси сосуда. В середине 90-х годов прошлого века было анонсировано открытие винтового движения крови в артериальных сосудах [19–21]. Суть этого открытия была сформулирована в статье [1]: « Теоретически и экспериментально обнаружено неизвестное ранее универсальное явление образования закрученного потока биологических сред в транспортных каналах человека и животных на примере сердечно-сосудистой, пищеварительной и мочевыделительной

Устинов Юрий Анатольевич, профессор кафедры теории упругости, Ростов-на-Дону систем..., обусловленное возникновением за счет трения соответствующих этому движению двух составляющих касательных напряжений при взаимодействии среды с волной скручивания, возбуждаемой в стенке канала сокращением спирально ориентированных мышечных и эластических элементов».

Анализ текста статьи показал, что теоретическая ее часть не содержит математической модели, объясняющей это явление, и, как следствие, не дается описания характера гидродинамического течения крови, а приводятся только интегральные характеристики течения, отражающие основные законы сохранения количества движения, момента количества движения и т.п., которые могут иметь место только для течений идеальной жидкости.

В работах [4, 12–14] описывается математическая модель и приведены некоторые результаты исследований особенностей движения крови, связанные с винтовой анизотропией механических свойств стенки сосуда, вызванной распределением мышечных волокон в виде винтовых спиралей [9, 10]. В частности, показано, что при пульсовом движении крови в силу винтовой анизотропии появляется вращательная составляющая скорости стенки сосуда, придающая движению частиц крови вблизи стенки сосуда винтовой характер в силу условия прилипания.

Следует обратить внимание на статьи [2, 3], в которых на основе нелинейных уравнений Навье–Стокса исследовалась задача течения жидкости в полуограниченной цилиндрической трубе, вызванного вихревыми возмущениями на входе. В этих работах показано, что спиральные возмущения проникают в трубу на конечное расстояние, зависящее от числа Рейнольдса, причем ниже по потоку формируется решение Пуазейля. На основе проведенных расчетов дается оценка этого расстояния и показывается, что результаты расчета достаточно хорошо согласуются с экспериментальными данными [8].

В работе [18] авторы, используя метод магнитно-резонансной томографии, исследовали движение крови на различных участках сердечно-сосудистой системы. Исследования группы добровольцев подтвердили возникновение и распространение винтового движения крови в артериальных сосудах в зависимости от ряда факторов, в том числе от кривизны и строения аорты. В работе [17] приводятся результаты экспериментальных исследований винтового движения крови на различных участках сонной артерии и связи винтового движения крови с определенными патологиями данной артерии.

В настоящей работе на основе математической модели, в которой сосуд рассматривается как полубесконечная упругая оболочка с винтовой анизотропией, а кровь как вязкая несжимаемая жидкость, исследуется движение всей системы и напряженно-деформированное состояние (НДС) стенки, порождаемые систолой. Проводится сравнительный анализ результатов расчетов с некоторыми экспериментальными данными, приведенными в работе [9].

О структуре стенки артериального кровеносного сосуда

Накопленный обширный экспериментальный материал позволяет рассматривать стенки артериальных сосудов как многослойные анизотропные оболочки [9, 10]. Согласно этим работам стенки всех артерий имеют сходное строение и состоят из одних и тех же материалов. Соотношения между материалами в стенках сосудов разных отделов системы кровообращения различны. В работе [10] выделены три основных типа артериальных сосудов: эластический, смешанный и мышечный. Традиционно стенка делится на три слоя: внутреннюю (интима), среднюю (медиа) и наружную (адвентиция) оболочки. Принято считать, что влияние интимы и адвентиции на механические свойства стенки незначительно, в силу чего упругие свойства оболочки определяются медией. Медиа состоит из множества концентрических слоев упругой ткани: эластина и мышечной ткани, оплетенных тончайшими волокнами коллагена. Полости между слоями заполнены различными губчатыми тканями и жидкостью. Относительная концентрация мышечной ткани и эластина определяет тип сосуда. Все мелкие артериальные сосуды относятся к мышечному типу [9]. Средний слой этих сосудов почти полностью состоит из спирально расположенных гладкомышечных клеток, размещенных также в виде слоев с незначительным количеством коллагена и эластина.

К этому же типу относятся все артерии головного мозга, а также подвздошная, поверхностная височная, плечевая и ряд других артерий [10]. В работе [7] отмечается, что угол между направлением волокон и продольной осью сосуда равен примерно 30°–50°.

На эластин, коллаген и мышечную ткань приходится около 50% материала стенки. Таким образом, материал стенки можно рассматривать как композит, упругие свойства которого определяются его компонентами: эластином, коллагеном, мышечной тканью, их взаимной концентрацией и геометрией распределения. Приведем некоторые сведения об упругих свойствах отдельных компонентов [9].

Эластин – нелинейно-упругий материал с модулем Юнга примерно E = 300 кН/м² для деформаций до 40%. Коллаген – более жесткий материал с модулем Юнга, равным примерно 10⁶ кН/м². Модуль Юнга гладких мышц существенно зависит от физиологического состояния и может меняться в пределах 100–1200 кН/м². Согласно экспериментальным данным, приведенным в книге [10], упругие свойства сосудов изменяются с возрастом.

Основные соотношения для оболочки с винтовой анизотропией

Стенку сосуда будем рассматривать как тонкую цилиндрическую оболочку. У сосудов мышечного типа упругие свойства стенки должны обладать винтовой анизотропией. Динамические уравнения цилиндрической оболочки с винтовой анизотропией приведены в работах [4, 12–14]. Чтобы не обременять заинтересованного читателя поиском этих работ, эти уравнения приводим ниже. Подчеркнем, что они получены на основе гипотез Кирхгофа–Лява и учитывают наличие предварительного напряженного состояния, которое присуще многим сосудам.

Артериальный сосуд будем рассматривать как полубесконечную цилиндрическую оболочку толщиной h и радиусом срединной поверхности a. С центром торца оболочки свяжем декартову систему координат Ox1x2x3 и введем винтовую систему координат r, 6, z , которая связана с декартовой соотношениями x1 = r cos(6 + T z), x2 = r cos(6 + T z), x3 = z, (1)

где a т = tg a , a - угол между касательной к винтовой мышечной спирали, расположенной на срединной поверхности стенки, и осью сосуда.

Предположим, что материал стенки ортотропный, и в базисе Френе винтовой спирали выполняется следующее условие:

e1 = n, e 2 = b, e3 = t, где n, b, t – орты главной нормали, бинормали и касательной соответственно, его свойства определены техническими константами E1,E2,E3,G12,G13,G23,v12,v13,v23 [5], которые удовлетворяют дополнительным условиям, вытекающим из условия положительной определенности удельной энергии деформации:

^ν 12 ^E 2 ^=ν 21 ^E 1^{, ν} 13 ^E 3 ^=ν 31 ^E 1^{, ν} 23 ^E 3 ^=ν 32 ^E 2^.

После перехода к базису винтовой системы координат в предположении, что

σ _rr =σ _{r θ} =σ _rz = 0 и x = a τ , получаем

σθθ	= g 11 e θθ	+ g 12 e zz	+ g 13 e θ z ,
σ zz	= g 12 e θθ	+ g 22 ezz	+ g 23 e θ z ,
σ θ z	= g 13 e θθ	+ g 23 e zz	+ g 33 e θ z

Здесь g11=[E2+x2(2ν32E2+4G23-4G23ν23ν32)+x4E3]/g0, g12 = [ν32E2 +x(E2 + 4G23 -4G23ν23ν32)+xν23E3]/g0, g22 =[E3 +x(4G23 - 4G23ν23 +2ν23E2ν32 )+xE2 ]/g0 , g13=x[E2(1-ν32)-2G23(1-ν23ν32)+x2(E3-E2ν32-2G23+2G23ν32ν23)]/g0, g23 = x[-2G23 (1- ν23ν32) + E3 (1-ν23 )+x(-E2 - E2ν32 - 2G23 + 2G23 -2G23ν23ν32)] /g0 , g33 =[(1 - ν23ν32)G23 (1 -x) +x(E2 -ν23E2 +E3 - E3ν32)] / g0, g0=(1 +x2)2(1 - ν32ν23).

Упрощения на основе гипотезы единой нормали приводят к выражениям eθθ =e1+α e1,  ez z=e2+y e2,  2eθ z=e3+y e3, e10=ur/a, e20=∂zuz, e30=∂zuθ ,

e11=0, e1=-∂2zur, e31=∂zuθ / a, где ur,uθ,uz – смещения точек срединной поверхности, -h/2≤y≤h/2.

В принятых выше обозначениях выражения для усилий и моментов можно записать в следующем виде:

T i = hg ij e ⁰ j , M i = h ³ g ij e ¹ j /12, где T 1 = T θθ , T 2 = T zz , T 3 = T θ z , M 1 = M θθ , M 2 = M zz , M 3 = M θ z .

Замыкают цепочку основных соотношений уравнения движения

∂ 2 M 2 T 1 T θ 0 z ∂ 2 u θ 0	∂ 2 ur ∂ z 2	- h ρ	∂ 2 ur 0 ∂ t 2 + q r = 0,
∂ z 2 aa ∂ zz
∂ T      ∂ 2 u 2 - h ρ 0     z + qz = 0, ∂ z        ∂ t 2 1 ∂ M 3 ∂ T 3 T θ 0 z ∂ ur	u		∂ 2 u θ+ q = 0. ∂ t 2 θ
	1 2 a 2	- h ρ 0
a ∂ z    ∂ z    a ∂ z    θ

Здесь ρ₀ = 0 – плотность материала оболочки, T _θ ⁰, T_z ⁰, T _θ ⁰ _z – усилия предварительно напряженного состояния.

Математическая модель пульсового движения крови В АРТЕРИАЛЬНЫХ СОСУДАХ

В предлагаемой математической модели колебания стенки сосуда описываются уравнениями предыдущего параграфа в предположении, что M _i = 0 (безмоментная теория), а движение крови – линейными уравнениями вязкой несжимаемой жидкости [6].

Будем считать, что на стенке сосуда выполняются кинематические условия прилипания

∂ _tu_r = v _r , ∂ _tu _θ = v _θ , ∂ _tu_z = v _z ,                                 (5)

а гидродинамическое воздействие на стенку сосуда выражается тем, что в уравнениях (4) имеют место соотношения qr=[p-2ρν ∂rvr]r=a, qz=-ρν[∂rvz+∂zvr]r=a,                                 (6)

q _θ =-ρν [ ∂ _r v _θ+ v _θ / r ] _{r = a} .

Здесь v _r ,v _z ,v _θ – радиальная, осевая и тангенциальная компоненты вектора скорости, p – давление, ∂ _r , ∂ _z , ∂_θ , ∂ _t – частные производные по соответствующим переменным.

Решение совместного движения отыскивается в виде

uj=Ujei(kς-ωt), vj(ξ, ς, t) = Vjei(kς-ωt), p = a-1ρνX1ei(kς-ωt),                   (7) ξ = r/a, ς=z/a, где ω – круговая частота, j= 1 ∼r, j=2 ∼z, j=3 ∼θ. На основании решения уравнений гидродинамики в предположении, что ∂r p = 0, имеем

V ( ξ , k ) = ik X + J 0 ( βξ ) X , V ( ξ , k ) = k 2 ξ X - ikJ 1 ( βξ ) X , z β 21 J 0 ( β ) 2 r 2 β 21 β J 0 ( β ) 2 (8) V θ ( ξ , k ) = 1 ( βξ ) X 3, β 2 = i γ 2 - k 2, γ 2 = a 2 ω / ν . J 1 ( β )

Здесь ν – кинематическая вязкость, X1 , X 2 , X 3 – произвольные постоянные, а амплитуды смещений Uj связаны с этими постоянными условиями прилипания

U_r = i ω^{- 1} V_r (1, k ), U_z = i ω^{- 1} V_z (1, k ), U _θ = i ω^{- 1} V _θ (1).                    (9)

Уравнения движения оболочки (4) совместно с соотношениями (5)–(9) позволяют свести задачу к однородной алгебраической системе уравнений dij(k,ω)Xj =0, i,j=1...3,                                  (10)

определитель которой, приравненный нулю, является дисперсионным уравнением.

Исследования, проведенные в [4, 12–14], показали, что при малых значениях волнового числа k это уравнение имеет шесть комплексных корней:

k s ^± , k s ⁺ = k s , k s ^- =- k s , Re k s > 0, s = 1,...,3.

Каждому корню отвечают элементарные волны (моды) давления, поля скоростей жидкости и смещений стенки:

ps±= X1±sei(±ksς-ωt), v±js =Vj(ξ,±ks)ei(±ksς-ωt), u±js =iUj(1,±ks)ei(±ksς-ωt).

Амплитуды скоростей получаются подстановкой X ₂ = X _{2 s} , X ₃ = X _{3 s} в выражения (8).

В приведенных выражениях X _js – решения однородной системы (10), которые для каждого значения s определяются с точностью до произвольной постоянной C_s .

В работе [13] приведены результаты исследования зависимости фазовых скоростей c_s ^± =± a ω /Re k_s , коэффициентов затухания K_s = Im k_s , коэффициентов координат скоростей

V (1, k )

njs = js, Vs =V1(1,ks)+V2(1,ks)+V3(1,ks) s от параметра α на частоте пульса f = 2Гц (ω =4π). Ниже рассматривается задача, моделирующая распространение пучка гармонических волн в артериальном сосуде, порождаемое систолой.

Обратимся к постановке краевой задачи.

Обозначим через T = 2 π / ω ₁ период сердечного цикла, где ω₁ – круговая частота пульса. Зададим на входе следующие граничные условия:

z = 0: p ⁰ = p_tm + p ( n ), V z (1,0, n ) = V (1,0, n ) = 0,                 (11)

где p m - давление на входе в сосуд при закрытом клапане; p ( n ) - избыточное давление, порождаемое систолой и открывающее клапан; η =ω ₁ t – безразмерное время; граничные условия для скоростей отвечают условиям прилипания.

Обозначим через η _c = 2 ε временной отрезок систолы и примем следующий закон изменения давления:

f =η ²( η-η _c )², 0 ≤η≤η _c ,                           (12)

f = 0, ηc ≤η≤2π.

Для построения решения представим выражение (12) в виде отрезка ряда Фурье. Имеем

N pN=pst+PRe[∑fne-in(η-ε)], po=ptm+Pf0,                    (13)

n = 1

где Pf ₀ = p _max - p ₀ , p _max – максимальное значение давления во время систолы, f_n , n = 0,..., N коэффициенты Фурье функции f , которые с помощью замены переменной вычисляются по формуле

ε f0 =      (ε2-η'2)2dη',

2π

ε fn =     (ε2-η'2)2cosnη'dη'

π

-ε

Решение будем отыскивать в виде

N 3

p = p ₀ + p ₁ a ς+ Re[ ∑∑ C_nsX _{1 ns}e^{i φ ns} ], n = 1 s = 1

N 3

v z = v⁰ z + Re[ ∑∑ C ns V zns e^{i φ ns} ],                           (14)

n = 1 s = 1

N 3

v θ = v⁰ θ + Re[ ∑∑ C ns V θ ns e^{i φ ns} ]. n = 1 s = 1

Здесь kns – корни дисперсионного уравнения, отвечающие значениям ω =nω1 , φns =knsζ-nη, Vzns , Vθns , получаются путем подстановки в выражения (8) k = kns , Xj = Xjns , где Xjns– частные решения однородной алгебраической системы (10), отвечающие значениям ω=nω1 , k = kns , Cns – произвольные постоянные, которые определяются при удовлетворении граничных условий (11); v0z , v0θ – скорость стационарного решения. Из [6] известно, что v0z=a2p1(1-ξ2) 4ρν есть решение Пуазейля, в котором p1 – градиент давления стационарного течения. Поскольку в момент открытия клапана среднее значение скорости vz равно нулю (расход равен нулю), значение p1 можно определить из условия

∫ ¹ v _z ξ d ξ= 0при z = 0, τ= 0.                          (15)

Решение линейных уравнений Навье–Стокса для v0θ , удовлетворяющее условиям прилипания, является сингулярным при ξ = 0 и имеет вид v0θ =C(ξ-1/ξ).                                  (16)

Постоянная C выражается через удельный момент количества M_z движения следующей формулой:

M_z = 2 πρ a ³v⁰ ξ ² d ξ=- πρ a ³ C .

Замечание 1. Результаты экспериментальных исследований [9] показывают, что в окрестности оси сосуда профиль скорости является практически плоским, что указывает на то, что если на входе в аорту в момент открытия клапана существует вихревое решение c v _θ ≠ 0, то оно за счет нелинейных конвективных членов уравнений Навье–Стокса преобразуется в течение типа Пуазейля. Об этом же говорят исследования [2, 3, 8].

Поэтому при проведении расчетов принималось v _θ = 0.

В работе [9] содержится обширный материал, иллюстрирующий нестационарное поведение различных полевых характеристик, таких как давление, градиент давления, максимальные и средние значения скоростей и др. Накопленный экспериментальный материал позволяет исследовать возможности той или иной математической модели. На основе этой концепции проводились исследования, о которых пойдет речь ниже. Однако полного набора параметров, содержащихся в данной модели, в известной авторам литературе не обнаружено (его, по-видимому, и не существует). Поэтому при проведении численных экспериментов значения некоторых параметров брались из работы [9] – a , h , E ₃ , а вязкость ν рассчитывалась по приводимым значениям чисел Рейнольдса для различных сосудов. Для нахождения численных значений g_ij , аналитические выражения которых содержат три модуля упругости, один из модулей E ₃ брался из работы [9], остальные параметры выбирались эвристически и варьировались. Подбор сопровождался контролем выполнения условий положительной определенности матрицы g_ij .

В качестве иллюстрации приведем некоторые результаты расчетов при следующих значениях параметров сосуда (аорта собаки) и крови: a = 0,73 ⋅ 10 ^{- 2}м , h = 0,6 ⋅ 10 ^{- 3}м , E ₃ = 4,905 ⋅ 10²кН/м² (согласно данным из работы [9] измеренные значения   E ₃ = (3 - 7) ⋅ 10²кН/м²),   E ₂ = 0,833 E ₃,   G = E ₃/4,   ν ₃₂ = 0,45,   ν ₃₂ = 0,54,

ρ ₀ = 115 кг/м³ , ν= 4 ⋅ 10 ^{- 6}м/с², ρ ₀ = 102 кг/м³ , α=π/6, круговая частота пульса ω ₁ = 4 π c ^{- 1}(2Гц) .

Продолжительность систолы принималась равной 1/3 сердечного цикла, из чего следует, что η= 2 ε= 2 π /3. При разложении функции f вида (13) ряда Фурье бралось девять членов ряда ( N = 8). При этом максимальная погрешность в равномерной метрике на отрезке 0 ≤η≤ 2 π менее 0,01.

Согласно работе [9] были выбраны следующие значения: p_tm = 10664, 47 Н/м² , P = 6660, 99 Н/м² или соответственно p_tm = 80 тор (мм рт. ст.), P = 50 тор. При этом градиент давления стационарного течения, определенный из условия (15), принимает значение p ₁ = 98,1 Н/м² .

Как отмечалось выше, каждой фиксированной частоте отвечают три волны ( s = 1...3). Ниже будем пользоваться терминами из работы [13].

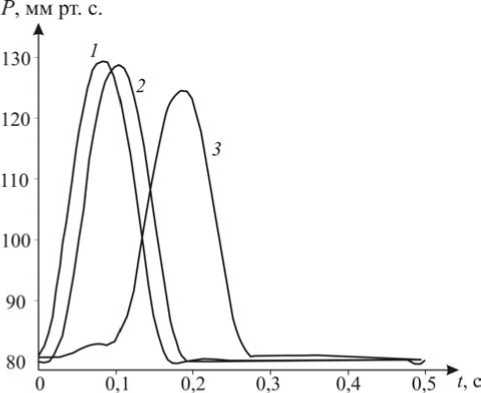
Рис. 1. Зависимость давления от времени: (1) z = 0; (2) z = 10, a = 7,3 см; (3) z = 50, а = 36,5 см grad p, кгс/м ’

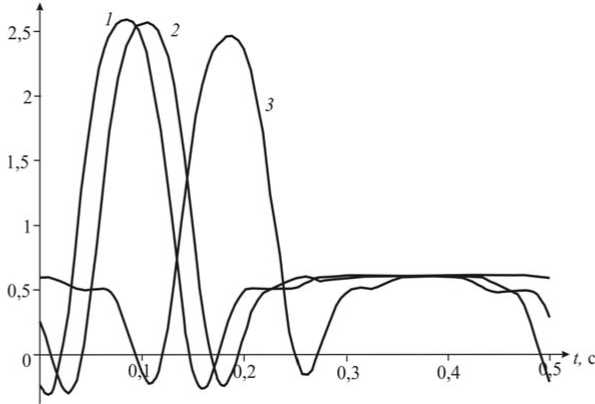
Рис. 2. Зависимость давления от времени: ( 1 ) z = 0; ( 2 ) z = 10, a = 7,3 см; ( 3 ) z = 50, а = 36,5 см

Зав исим ости фазовых скорос тей и коэфф ицие нтов затухания от частоты

c1 c2 c3 K1 ⋅10-3 K2 ⋅10-3 K3 ⋅10-3 17,64 7,47 3,94 1,07 1,61 0,856 18,86 7,94 3,98 1,60 2,55 1,16 19,47 8,17 4,00 2,02 3,29 1,39 20,14 8,33 4,01 2,37 3,92 1,58 20,36 8,44 4,02 2,68 4,47 1,76 20,52 8,52 4,02 2,96 4,98 1,91 20,67 8,58 4,03 3,23 5,45 2,05 изменяются, а фазовая скорость волны давления фактически постоянна. Это означает, что заданная на входе в сосуд форма давления должна распространяться по стволу сосуда, сохраняя свою форму с незначительным уменьшением амплитуды (в силу малости коэффициентов затухания).

Затухание же в данной математической модели определяется только вязкостью жидкости. На рис. 1 приводятся графики, иллюстрирующие зависимость давления от времени на временном отрезке, равном одному циклу, в различных сечениях z = const. Кривая 1 отвечает z = 0, кривая 2 – z = 10 , a = 7,3 см, кривая 3 – z = 50, a = 36,5 см .

Замечание 2. Следует отметить, что длина прямолинейного участка аорты собаки равна примерно 3 см [9]. Поэтому выбор сечений z = const был продиктован следующими целями: наглядно проиллюстрировать отсутствие дисперсии и степень затухания.

Следует также отметить, что наблюдаемые в конце систолы всплески на экспериментально отснятых графиках давления («дикротический зубец»), как сказано в [9], указывают на закрытие клапана, что в данной модели не учитывается. Кроме того, всплеск может быть порожден отраженными волнами от границы перехода прямолинейного участка аорты в криволинейный. Действительно, если учесть, что выбранный временной отрезок систолы t s = 0,666 с , фазовая скорость самой медленной волны давления с₃ = 4 м/с, то общее время пробега прямой и обратной волн прямолинейного участка аорты t p = 0,015 с. Следовательно, за отрезок времени t s может произойти 44 переотражения, которые даже при незначительном значении коэффициентов отражения могут явиться причиной появления «дикротического зубца».

На рис. 2 приводятся графики поведения градиента давления в указанных выше сечениях.

Рис. 3 отражает поведение во времени расхода Q в различных сечениях. Следует отметить, что расчетные графики достаточно хорошо отвечают экспериментально отснятым кривым расхода.

Рис. 4 иллюстрирует распределение скорости v _z по сечению сосуда z = 3 a в моменты времени t₁ = 1/ to , » 0,8 с . Кривая 1 отвечает трехмодовой теории, кривая 2 – одномодовой (волне давления).

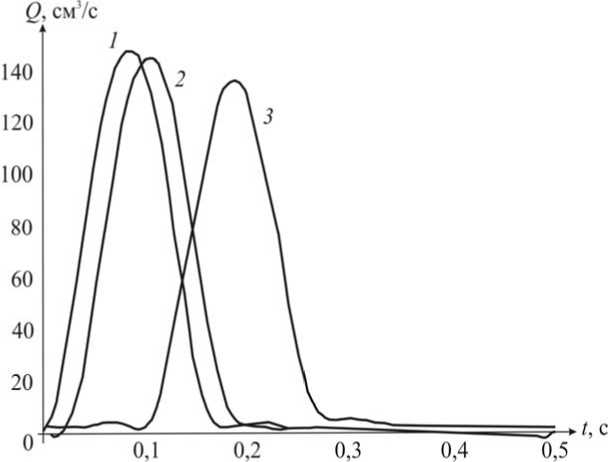
Рис. 3. Зависимость расхода Q от времени t : ( 1 ) z = 0; ( 2 ) z = 10, a = 7,3 см; ( 3 ) z = 50, а = 36,5 см

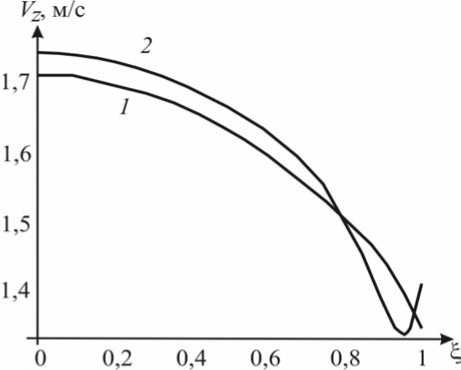
Рис. 4. Распределение скорости V_z по сечению сосуда z = 3 a : 1 – результаты, полученные по трехмодовой теории; 2 – по одномодовой теории (волне давления)

V, м/с

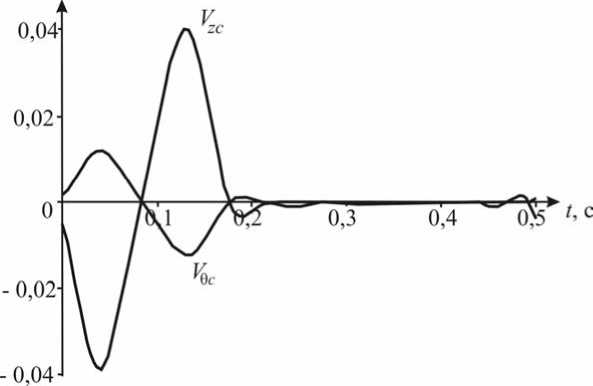
Рис. 5. Распределение скоростей V zc и V θ c в сечении z = 3 a в зависимости от времени

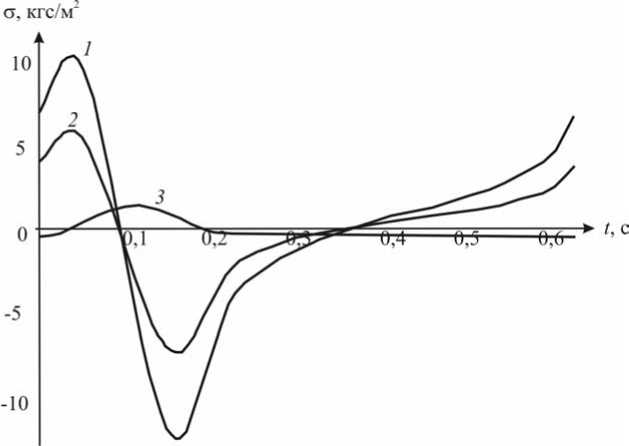
Рис. 6. Зависимость распределения напряжений во времени при z = 10 а и а = 30 ° : 1 - ст _zz ;

2 – σ_θθ ; 3 – σ _{z θ}

Рис. 5 иллюстрирует поведение во времени скоростей стенки сосуда V_zc (кривая 1 ) и V _{θ c} в сечении z = 3 a . Для выбранного значения α =π /6 отношение max V_zc /max V _{θ c} ≈ 3 , для α=π /100 это отношение равно примерно 10.

Для сравнения с экспериментальными данными, приводимыми в работе [9], рассмотрим следующие результаты расчета: среднее по сечению и по времени значение скорости v _z = 0,163 м/с попадает в вилку экспериментальных значений 0,1–0,4 м/с, рассчитанное пиковое значение скорости на оси, равное примерно 1,6 м/с, попадает в вилку 0,4–2,9 м/с.

Описанные результаты расчета опирались на трехмодовую теорию. Параллельно были проведены аналогичные расчеты основных гидродинамических характеристик движения крови (давления, градиента давления, расхода, распределения скоростей по сечению и др.) по одномодовой теории, согласно которой распространение давления и средней по сечению скорости вдоль оси сосуда описывается уравнениями

∂ ² _zp - c ₀ ^{- 2} ∂ _t ² p = 0, ρ∂ _t v =-∂ _zp .

Проведенный сравнительный анализ показал, что практически все гидродинамические характеристики с высокой степенью совпадения описываются одномодовой теорией. Отличие наблюдается только в распределении скоростей вблизи стенки сосуда.

Приведем некоторые результаты анализа напряженного состояния стенки. Такой анализ полезен, в частности, для понимания необходимости предварительного натяжения, которое присуще многим артериальным сосудам.

Кратко опишем схему, на основе которой проводились расчеты напряжений.

Представления для напряжений в виде отрезков рядов Фурье получались путем подстановок (14) → (5) → (3) → (2).

Рис. 6 иллюстрирует поведение во времени при z= 10 а и а = 30 ° напряжений ст zz (кривая 1 ), σ_θθ (кривая 2 ), σ _{z θ} (кривая 3 ). Кривая 1 наглядно иллюстрирует, что при отсутствии предварительного натяжения в стенке сосуда во время систолы возникает продольное сжимающее напряжение. Может ли сжатие во время систолы привести к потере устойчивости стенки сосуда? Этот вопрос остается открытым и требует дополнительных исследований. Тем не менее предварительные растягивающие напряжения уменьшают вероятность возникновения этого явления. В рассмотренном случае, для того, чтобы на всем периоде сердечного цикла выполнялось условие σ _zz >0 , достаточно, чтобы T_z ⁰ > 1,5 ⋅ 10³кгс/м².

Заключение

Рассмотренная модель пульсового движения крови в полубесконечном артериальном сосуде, учитывающая винтовую анизотропию его стенки, естественно, далека от совершенства. Вместе с тем проведенные на ее основе расчеты и сравнительный анализ с экспериментальными данными показали, что она с достаточной степенью точности отражает поведение основных гидродинамических характеристик при развитии движения. Следует подчеркнуть, что на входе в сосуд задавались только давление и условия жесткой заделки сосуда в стенку сердца, что в рассмотренной модели эквивалентно обращению в нуль продольной и крутильных скоростей на границе отверстия. Остальные характеристики, такие как расход, средняя и пиковая скорость, напряжения в стенке сосуда, определялись на основе построенного решения. Численные значения этих характеристик попали в вилку экспериментально измеренных значений [9]. Как показали расчеты, влияние винтовой анизотропии на эти параметры в выбранном для анализа сосуде оказалось незначительным. Это влияние на скорости существенно только в окрестности стенки сосуда. Однако функции артериальных сосудов сводятся не только к переносу крови. Они выполняют еще одну, не менее важную функцию – сквозь их стенки осуществляется доставка кислорода и лекарственных веществ. По-видимому, распределение мышечных волокон в виде винтовых спиралей оказывает существенное влияние на проницаемость и массоперенос при динамических процессах в стенке сосуда. Кроме того, мышечная ткань в стенке сосуда выполняет еще одну важную функцию – функцию «распределенного сердца» [1, 15, 16], осуществляя дополнительную «подкачку» в периферийной части кровеносной системы.

Благодарности

Работа выполнена при финансовой поддержке Южного федерального университета и Российского фонда фундаментальных исследований (код проекта 07-01-00254а).