Модель формирования и роста сети локализации знаний

DOI:

Сосуществование городов разного масштаба – отличительная черта российской экономической модели. Вместе с тем гармоничность и сбалансированность развития городов, от малого до крупнейшего масштаба, до сих пор относится к актуальной научной задаче. Так, в экономико-математической модели, посвященной управлению демографическими процессами, сценарий дезурбанизации формирует аргументы для более оптимистичного прогноза роста численности населения [Цифровой двойник … , 2022]. Несмотря на то что дезурбанизация, в первую очередь, характеризуется изменением соотношения городского и сельского населения, повышение статуса малых и средних городов также можно отнести к ослаблению процесса урбанизации. Не снижается значимость полноценной интеграции муниципальных образований в стратегические документы России [Кузнецова и др., 2024]. Одной из сфер, на основе которой можно судить о положительной динамике развития города, является наука. Однако, существующая система показателей не позволяет получить реальную картину научного потенциала города. Как правило, апробация моделей для оценки уровня территориальной науки привязана к количеству объектов интеллектуальной собственности, численности исследователей и объему финансирования науки [Гав-рилец и др., 2022], что хорошо описывает позицию той или иной территории, но слабо характеризует внутренние территориальные процессы формирования и преобразования знаний. Ввиду низких значений перечисленных показателей, большое количество городов выходит за границы статистической значимости.

Принимая во внимание первостепенную важность исследователя для появления знаний в городе [Самоволева, 2022], сместим акцент с количества исследователей и их результатов на характер их взаимодействия, то есть на связи, обеспечивающие формирование знаний. В научной литературе такой подход моделируется теорией графов [Bianconi et al., 2001; Di Bella et al., 2021; Newman, 2001]. Выявлено, что сеть малого города, построенная на основе выборки патентов на изобретения и полезные модели, представляет собой несвязное множество групп исследователей, растущих с разной скоростью [Мельникова, 2023]. Подобная ситуация характерна для городов любого размера с различиями в количестве компонент связности (групп) и характере их роста, будучи результатом разнообразия организаций и направлений исследования. Все компоненты связности на изначальном этапе представляют собой полный граф и имеют такой дальнейший рост, который поддерживает высокий уровень кластеризации.

Сеть, состоящую из локальных групп исследователей, будем рассматривать как сеть локализации знаний в конкретном городе. В общем смысле под локализацией знаний понимаем целенаправленный и устойчивый процесс накопления знаний на определенной территории. Тогда целью данной статьи будет построение экономико-математической модели для объяснения динамики сети локализации знаний в городах разного масштаба.

Пространственные требования не позволяют использовать действующие модели растущих сетей. Во-первых, существующие модели растущих сетей представляют собой формирование графа в форме единой компо- ненты. Во-вторых, появление новой связи (ребра) у вершины зависит либо от абсолютной случайности, либо от количества старых связей (ребер) вершины. В наиболее распространенной модели Барабаши – Альберт решение об образовании связи принимает вершина, которая появляется в сети позже. Научная сеть фактически представляет собой противоположный процесс, когда участники группы исследователей, сформированной на более раннем этапе, включают в свой коллектив новичков (появившихся на более поздних этапах).

Ближе всего к объяснению появления связи между исследователями находится теория игр, которая исходит из максимизации полезности и предполагает сопоставление игроками стратегий. Например, через антога-нистическую игру можно описать взаимодействие врача и пациента [Сигал, 2023].

В нашем случае построение взаимодействия происходит совместно с ростом сети, что моделируется в рамках подходов, объединенных в отдельный раздел теории игр, который ищет решение для двух связанных групп задач: выработка правила формирования ребра и объяснение на его основе характера роста сети.

Теоретические подходы к формированию сети на основе стратегического взаимодействия

Правило формирования ребра дифференцируется в зависимости от разной трактовки выгод и затрат. Формирование ребра может зависеть от ценности вершины и удаленности от нее [Jackson et al., 1996, p. 49]:

ui(g)=ωij+∑δd(i,j)ωij- ∑cij, (1) j≠i j:ij∈g где ωij – ценность вершины j для вершины i; cij – затраты, связанные с наличием ребра; δd(i, j) – выгода, связанная с наличием ребра, которая меняется в зависимости от длины наименьшего пути между i и j, δ ∈ (0,1).

Подходы к формированию ребра различаются исходя из направления потока выгод для вершин: одностороннего или двустороннего [Bala et al., 2000]. В первом случае обра- зуется ориентированная сеть, в которой только один из двух игроков будет получать выгоду, например, игрок i от ребра к j (направление ребра от j к i). Во втором случае речь идет о неориентированной сети. В обоих случаях при определении выгоды авторы учитывают количество ребер в пути между i и j (мi(g), а при определении затрат только прямые ребра (мid(g)), умноженные на затраты на каждое ребро (c). В результате полезность для игрока будет равна [Bala et al., 2000, p. 1190]:

u_i ( g ) =м_i ( g ) – м_i^d ( g ) c . (2)

Отмечается, что теоретико-игровой подход позволяет объяснить формирование замкнутых триад, способствующих высокой кластеризации реальных сетей знаний. Авторы [Jackson et al., 2005] приводят модель, представляющую собой формирование сети как определенного количества сильносвязных компонент («островов»), попарно соединенных между собой одним ребром (в равновесии). Сильносвязные компоненты образуются ввиду более низкой стоимости (или более высокой полезности) образования ребра между вершинами, схожими по характеристикам. Данный факт можно моделировать через требование к минимальному пути между двумя вершинами, которое дифференцирует выгоду, или через принадлежность вершин к одной группе по интересам (научным, социальным, политическим и т. д.). Тогда полезность будет выражаться как ui(g)= ∑ δd(i,j) - ∑cij (3) j≠i:l(i, j)≤D j:ij∈g , где cij – затраты, связанные с наличием ребра (если i и j принадлежат к одной группе, то cij=c, если разным cij=C, то, где C > c > 0); δd(i, j) – выгода, связанная с наличием ребра, которая меняется в зависимости от длины наименьшего пути между i и j (если расстояние между i и j превышает некоторую величину D, тогда выгода отсутствует).

Предлагается также модель, в которой в формуле полезности учитывается коэффициент кластеризации [Brautbar et al., 2011, p. 229]:

u_i ( g ) =Clust_i – α · deg_outi , (4)

V, где Clust = —2коэффициент кластеризации, где i Cd2egi как результат деления количества треугольников у вершины i к общему количеству пар соседей вершины i; α – одинаковые для всех игроков затраты на ребро; degouti – исходящая степень вершины i.

В выше приведенных моделях по мере увеличения количества ребер у вершины растет дополнительная полезность. Однако бывают случаи, когда рост числа ребер у одной вершины снижает полезность для других вершин. Такой подход используется для описания совместных научных исследований [Jackson et al., 1996]. Если рассматривать ребро как отдельный научный проект между исследователями, тогда на каждый такой проект уделяется определенное время. В результате, чем больше у исследователя проектов, тем меньше времени он тратит на каждый из них. Тогда формула полезности будет иметь вид:

ui (g) = 2® i (ni, j, nj) - c (ni), (5) j :j eG где ωi(ni,j,nj) – полезность для вершины i от прямого контакта с j; ni,nj – исследовательские проекты, в которые вовлечены соответственно i и j. При равном распределении времени, доступного исследователю на проекты, полезность будет определяться в виде:

u i ( g ) = 2 [-1+-+—] (6) ^,

j:ijeG ni nj ninj где 1 / (ni,nj) – синергия от исследовательского проекта. В данном случае затраты на ребро интегрированы в логику снижения ценности по мере добавления каждого нового взаимодействия.

При формировании ребра может учитываться и некоторая вероятность (внешнее воздействие), дополняющая результат принятой стратегии [Jackson, 2008].

Затраты на формирование ребра также могут содержать несколько составляющих: единовременные расходы на присоединение ребра (несут только инициаторы ребра), затраты на поддержание связи, а также расходы, стимулирующие заключение соглашения о формировании ребра [Atabati et al., 2015]. Объем ресурсов, который игрок способен направить на потенциальные связи, может быть ограничен, что формулирует задачу эффективного распределения ресурса. Может также использоваться понятие силы и надежности связи между игроками i и j. Сила связи определяется как сумма ресурсов, направленных ими на совместное ребро. Выбирая наиболее надежную связь, игрок i полагается на наиболее сильные связи по пути к j [Goyal, 2009].

В другой интерпретации сила связи может быть представлена как сумма индивидуальной способности игроков к построению связи (например, уровень точности передачи информации):

g_ij = β _i ( c_ij ) + β _j ( c_ji ) . (7)

Тогда выгода для вершины i от ребра с вершиной j может выражаться как

I i ( g ) = 2 vjg j j e N i ( g )       ,

где ν_j – доля информации, которая поступает к i от j [Olaizola et al., 2024].

Правило формирования ребра в сети локализации знаний

Описание сети. Сеть локализации знаний представляет собой несвязный граф, состоящий из нескольких компонент связности разного типа. Каждая из компонент связности на изначальном этапе представляет собой полный граф, который можно обозначить как K_n ( n >  2). В динамике K_n может иметь или не иметь рост, поэтому типы компонент связности можно охарактеризовать следующим образом:

• 1.    Полный граф «без роста». В данном случае K_n в динамике не меняется. Это означает, что поддерживается постоянный состав группы исследователей.

• 2.    Полный граф «с ростом через одну вершину». Динамика K_n представляет собой добавление в группу новых вершин с ребрами, которые присоединяются только к одной вершине группы K_n (см. рис. 1, а ).

• 3.    Полный граф «с ростом через группу вершин». Динамика K_n предполагает, что часть или все вершины K_n присоединяют к себе одну или несколько новых вершин. Таких подмножеств в изначальном K_n может быть несколько (см. рис. 1, б , в , г ).

  

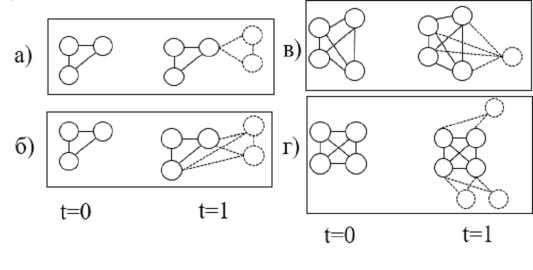
  Рис. 1. Типология роста компонент связности (групп исследователей) сети локализации знаний

  
  

Fig. 1. Typology of connectivity components (research groups) growth in knowledge localization networks

Примечание. Составлено автором. Отображен один этап роста группы исследователей от t = 0 до t = 1. Сплошная штриховка – это изначальные вершины и ребра, пунктирная штриховка – вершины и ребра, появившиеся на t = 1.

Note. Compiled by the author. Shows one stage of growth of the research group from t = 0 to t = 1. Solid hatching represents the original vertices and edges; dotted hatching represents the vertices and edges that appeared at t = 1.

Зафиксируем многообразие исследовательского сообщества через уровень индивидуальных знаний ( k_i ), которым обладает каждая вершина. В целом существуют разные подходы к фиксации уровня интеллекта и способностей исследователя. Можно, например, использовать сочетание таланта и труда [Ис-лакаева и др., 2016]. Такой подход хорошо интегрируется в задачу оценки продуктивности конкретного исследователя. В нашем случае необходимо запустить процесс накопления знаний, поэтому будем считать, что индивидуальные знания включают в себя набор знаний (концепции, методы, практические результаты), представляя собой своего рода относительную позицию исследователя в научном сообществе. Будем считать, что самый большой уровень индивидуальных знаний в 10 раз превышает наименьший, учитывая при этом, что k_i не принимает нулевое значение, то есть ( k_i = {10,20,30, …, 100}). Такой подход позволяет учитывать территориальный фактор, допуская разную вероятность появления вершин с высоким уровнем индивидуальных знаний в городе.

Правило формирования ребра. Ввиду того, что потенциальные участники расширения существующей группы исследователей появляются в сети позже, поэтому фактически будет возникать ситуация включения их в группу (без учета их мнения). В результате стратегическое взаимодействие по поводу образования новых ребер будет проходить между участниками существующей группы исследователей. Кроме того, в качестве допущения примем, что присоединение нескольких вершин предполагает формирование полного графа, что отображено на рисунке 1.

Исследователь оценивает полезность образования новой связи не только исходя из потенциального изменения его индивидуальных знаний, но и с учетом формирования совместных знаний. Совместные знания ( K ( g )) представляют собой новые знания, образованные в результате работы группы исследователей над проектом, которые сформированы из вклада каждого автора и синергетического эффекта.

Индивидуальные знания изменяются согласно

Δki(g) = ∑α(kj -ki), (9) j:ij∈g где а - доля индивидуальных знаний исследователя, которую он передает другому. Можно наблюдать отток или приток индивидуальных знаний (то есть на очередном этапе ki берется с учетом Δki(g)). Такая ситуация возможна, так как мы зафиксировали, что индивидуальные знания представляют собой относительную позицию автора, а не абсолютное значение его интеллектуальных возможностей. В рамках группы исследователей обмен индивидуальными знаниями происходит один раз.

Трудность формализации совместных знаний, в первую очередь, связана с описанием синергетического эффекта по результатам работы группы исследователей [Романов и др., 2023]. Некоторые авторы в качестве синергетического эффекта рассматривают интеллект человека как своеобразный мультипликатор [Филин и др., 2020]. В любом случае, синергетический эффект должен инкорпорировать положительное влияние на участников группы [Цуриков и др., 2024]. На наш взгляд, совместные знания формируются следующим образом:

n

K ( g ) = c ^eE k i 0 ,            (io)

i = 1

где c – мультипликатор синергетического эффекта; P - доля индивидуальных знаний исследователя, которая направляется на совместную работу (P > а); n – количество исследователей в группе. Предполагается, что каждый участник группы имеет доступ к совместному знанию в полном объеме. Индивидуальные знания, направляемые на совместную работу, не снижают их уровень у конкретного исследователя. Мультипликатор синергетического эффекта позволяет варьировать продуктивность группы.

В терминологии теории игр каждый участник стремится максимизировать изменение индивидуальных знаний и объем совместных знаний, что будет рассмотрено в рамках двух параллельных игр.

В матричном виде игры могут быть записаны следующим образом (рис. 2).

Допустим изначальная группа исследователей представляет собой полный граф на трех вершинах со следующим уровнем индивидуальных знаний: к, = 50, к_К = 30, k = 15, А 0             Б 0             В 0

а также а = 10 %, P = 20 %, с = 2.

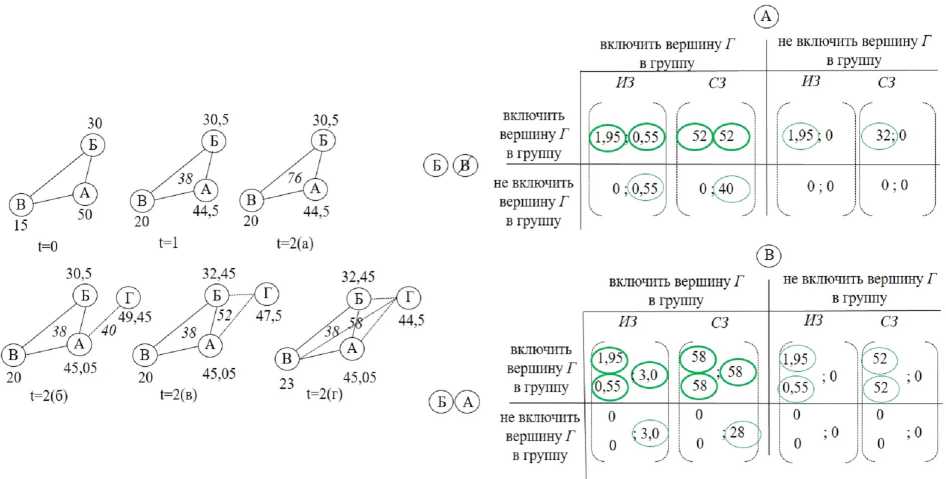
Рис. 2. Обоснование решения о формировании ребра на основе стратегического взаимодействия в группе исследователей

Fig. 2. Justification of the decision to form an edge based on strategic interaction in a research group

Примечание. Составлено автором. Рассмотрен случай присоединения одной вершины ( Г ). Для удобства, обе игры записаны в рамках одной матрицы, но реализуются отдельно. ИЗ – игра по индивидуальным знаниям. СЗ – игра по совместным знаниям. Лучшие ответы выделены кружком зеленого цвета, в том числе равновесие по Нэшу – с более жирной границей. В первой матрице представлено взаимодействие вершин Б и А , при условии отказа от участия вершины В . Во второй матрице – вершин Б и А (верхние значения для Б , нижние – для А ), с одной стороны, и вершины В , с другой стороны.

Note. Compiled by the author. The case of joining one vertex ( Г ) is considered. For convenience, both games are recorded within the same matrix but are implemented separately. ИЗ is a game of individual knowledge. СЗ is a game of joint knowledge. The best answers are highlighted with a green circle, including the Nash equilibrium – with a thicker boundary. The first matrix shows the interaction of vertices Б and А , subject to the refusal of vertex В to participate. The second matrix shows vertices Б and А , on the one hand (upper values for Б , lower values for А ), and vertex В , on the other hand.

На первом этапе каждый исследователь из группы передал друг другу знания: kA, = k A 0 + ^А k A = ^44,5, где a k_A = - 5,5; ^кБ 1 = ^кБ 0 ^{+ А к}Б = ³⁰,^5, где А к_Б =+ 0,5^; к В = ^к В₀ + А к_в = 20, где А к В = 5,0. Проведено научное исследование, которое дало совместные знания в объеме K₁ ( g_АБВ ) = 38 единиц (рис. 2, t = 1). На втором этапе в случае сохранения такого же состава группы, образуются новые совместные знания, что дает в сумме K₁ ( g_АБВ ) + K₂ ( g_АБВ ) = 76 единиц, уровень индивидуальных знаний каждого исследователя остается прежним (рис. 2, t = 2(а)).

Предположим, что на втором этапе в сеть добавляется одна вершина k_Г = 50, тогда исследователями будут рассматриваться следующие варианты ее включения в состав группы: к одному исследователю, к некоторой части исследователей, ко всем исследователям. Всего может быть 7 вариантов присоединения. На рисунке 2 представлены три варианта относительно вершины А ( t = 2(б), t = 2(в), t = 2(г)).

Определим равновесие по Нэшу отдельно для индивидуальных и совместных знаний. В части индивидуальных знаний лучший ответ А на стратегию Б «Включить вершину Г в группу» (без В ) будет также участвовать в этой группе. И даже если Б решит не участвовать в группе, А получит от участия дополнительные индивидуальные знания в объеме 0,55 ( к_Аг = 45,05, где А к_А = + 0,55).

Исходя из образования совместных знаний для А – участие в группе с Г также лучший ответ на любую из стратегий Б . Для Б ситуация абсолютна идентична. Соответственно, для обоих участников включение Г в совместную группу – это строго доминирующая стратегия или равновесие по Нэшу. Дальнейшее изучение выбора стратегии проводится путем сопоставления стратегии А и Б (одновременно) с одной стороны и стратегии В , с другой. Строго доминирующие стратегии также представляют собой включение Г в совместную группу. Такой же вывод справедлив и для других вариантов присоединения.

Если индивидуальные знания вершины Г меньше, чем у некоторых участников группы (например, kГ= 40), возникает иное равновесие. Сильно доминирующей стратегией для А в части индивидуальных знаний является не ра- ботать с Г, а в части совместных знаний – взаимодействие. В таком случае, если А откажется, а Б и В скооперируются с Г, тогда уровень их совместных знаний составит 34 единицы, что меньше, чем результат совместной работы А и Г (36 ед.), А, Б и Г (48 ед.) и А, Б, В и Г (54 ед.).

В результате каждая игра формирует свое множество равновесий по Нэшу. Введем следующие обозначения: вместо стратегии «Включить вершину Г в группу» будем использовать В , «Не включить вершину Г в группу» – Н. Соответственно, ВВ – это равновесие, в котором оба исследователя выбрали стратегию В .

Первое множество будет состоять из элементов, представляющих собой набор равновесий по индивидуальным знаниям каждого из исследователей группы:

ИЗ = { ИЗ а ,..., ИЗ п } , (11)

где n – количество исследователей в группе; ИЗ_n – набор равновесий по индивидуальным знаниям n -ого исследователя из группы. Набор равновесий извлекается из надмножества, которое представляет собой все возможные равновесия по Нэшу n -ого исследователя с учетом разного уровня индивидуальных знаний новой вершины, то есть { ВВ , НВ , ВН , НН} ^ ИЗ_п .

Все равновесия по Нэшу в части совместных знаний будут иметь вид ВВ , а отличия заключаются в количестве исследователей группы, которые образуют ребро с новой вершиной. Соответственно, второе множество будет состоять из трех элементов:

СЗ = { СЗ ₁, C3 i , СЗ п } , (12)

где нижний числовой индекс интерпретируется как 1 – ребро с вершиной Г сформировано единственным исследователем из группы; l – некоторым количеством исследователей; n – всеми исследователями.

Тогда рост группы исследователей будет определяться результатом сочетания двух множеств, формат записи которого будет включать равновесие по индивидуальным знаниям с нижним индексом, отображающим равновесие по совместным знаниям (например, ВВСЗ ). Следуя логике [Клейнер, 2012] сочетание можно рассмотреть через объеди- нение и пересечение множеств равновесий. Определим также, что результат по совместным знаниям главенствует над результатом по индивидуальным знаниям, то есть СЗ > ИЗ. Такая ситуация характерна для большинства служебных изобретений в силу применения системы вознаграждения за полученный научный результат (подтвержденный охранным документом).

Объединение множеств предполагает результат, основанный на максимизации совместных знаний. Соответственно, из множества равновесий будет выбрано то, в котором все исследователи обретут наибольший объем по совместным знаниям. Такая ситуация всегда будет приводить к росту группы через все вершины, а именно: ИЗ и СЗ = ВВ _СЗ^ .

Пересечение множеств предполагает результат, который не давал бы 1) строго сильного преимущества по изменению индивидуальных знаний и объему совместных знаний одновременно и 2) ухудшений относительной позиции каждого исследователя. Рассмотрим три случая.

Случай 1. Уровень индивидуальных знаний присоединяемой вершины превышает уровень индивидуальных знаний каждого из исследователей группы. В результате все исследователи из группы придерживаются стратегии В . В данном случае, пересечение множеств равновесий будет давать результат ИЗ п СЗ = ВВ_СЗ , который соответствует группе, состоящей из исследователя с наибольшим приростом по индивидуальным знаниям (следовательно с наименьшим объемом по совместным знаниям) и новой вершины. Для примера, представленного на рисунке 2, это будет группа ВГ .

Случай 2. Все исследователи из группы придерживаются стратегии Н . Такая ситуация возможна, когда уровень индивидуальных знаний новой вершины меньше, чем у каждого из исследователей группы. Тогда пересечение множеств равновесий будет пустое множество, а именно: ИЗ п СЗ = {}.

Случай 3. Уровень индивидуальных знаний присоединяемой вершины ниже уровня индивидуальных знаний одного или нескольких исследователей из группы. Тогда пересечением множеств равновесий будет совместное участие в новой группе исследователей, у которых по индивидуальным знаниям была стратегия Н в образовавшихся равновесиях НВ, а именно: ИЗ п СЗ = НВсз для одного исследователя и ИЗ п СЗ = НВсз для нескольких исследователей.

Например, если к Г = 30 , тогда:

ИЗ а = { НН Б , НВ ав } ,     ИЗ_Б = { НВ_БВ , НН_БА } ,

ИЗ_В = { ВН ва , ВН вб } ,

СЗ_А = { 32, 44,38, 50 } ,       СЗ Б = { 24, 44,30, 50 } ,

СЗ_В = { 18, 38,30, 50 } .

Результатом пересечения будет создание группы в составе А, Б, Г :

ИЗ п СЗ = {НН.Б, НВ. „, НВБв, ННБ., ВНв., ВНвг}п АБ     АВ     БВ      БА      ВА      ВБ п {32АГ,24БГ,18ВГ,44АБГ,38АВГ,30БВГ,50АБВГ} = АБГ•

Дадим пояснение. Несмотря на то, что А и Б теряют в уровне индивидуальных знаний, они приобретают совместные знания. Вместе с тем вершина В ничего не теряет, но и не приобретает. Любое участие В даст ей преимущество перед другими вершинами.

Факторы роста сети локализации знаний

Постепенное расширение группы будет сопровождаться разным масштабом изменений индивидуальных знаний для участников, что в результате может привести к одинаковому уровню индивидуальных знаний. Такая ситуация эффективна с точки зрения баланса в группе, однако не эффективна с позиции тех исследователей изначальный уровень индивидуальных знаний которых был выше.

Сформулируем уравнение динамики для изменения во времени индивидуальных знаний участника. Оно имеет форму разностного уравнения

• к, = к, + а ( V к, - т,к, ) =

it        it - 1          ⁴ ^^ Зг         it it - 1 ⁷

• j : ij ; j e gt - i

• = (i — ma ) ^k _/ t - 1 + ^a ^ ^k jt ,       ⁽¹³⁾

jv ; j e gt - 1

где mi – количество новых ребер вершины i на эта-t пе t; X - - сумма индивидуальных знаний по новым;'. . шинам которые присоединились к i на этапе t (индекс j e gt-1 подразумевает, что в составе группы исследователей предыдущего этапа данных вершин не было). Решение данного уравнения будет иметь следующий вид, выраженный через изначальный уровень индивидуальных знаний исследователя:

к = П (1 - "М-К ♦ £ а X ‘ лИтТ^ • (14)

/=0                      к = 0 j : ij ; i t gt - i 4 ⁽1 ^{- m} _k « )

Если предположить, что в рамках примера (см. рис. 2) на каждом этапе присоединяется одна вершина с уровнем индивидуальных знаний k_j =50 и с одним ребром, тогда по отношению к вершине А изменение индивидуальных знаний для первых трех этапов будет таково: k_А = 44,5, k_А = 45,05, k_А = 45,54.

В случае, если все другие иссл³едовате-ли из группы выбирают включение в группу данной вершины, тогда на третьем этапе результат для остальных вершин будет следующий: k_Б =34,2 и k_В = 25,7. К третьему этапу запас зна³ний вершин³ ы А снизился на 8,92 %, вершины Б и В вырос на 14 и 71,3 % соответственно.

Если предположить, что (1 - m_i α ) и α ∑ k_j j : ij ; j ∉ g_{t - 1} являются константами, то есть на каждом этапе в сеть добавляется одинаковое количество вершин и ребер (тем самым исключается нижний индекс t ), тогда мы получим автономное разностное уравнение, которое можно оценить с позиции сходимости к устойчивому состоянию.

k_it = (1 - m_i α ) ⋅ k_{it - 1} +α ∑ k_j .      (15)

j : ij ; j ∉ g _{t - 1}

Решением такого уравнения будет kit =(1-miα)t ⋅ki0 +α ∑kj j:ij; j∉gt-1

(1 - (1 - m i α ) ^t ) m_i α

. (16)

Полученное уравнение зависит только от изменения выражения (1 - mi α), так как оно единственное зависит от t. Устойчивое состояние характеризуется ситуацией, когда ki = ki ≡ ki . Произведем соответствующую замену в уравнении (15) и получим ki = (1- miα) ⋅ki + α ∑kj.

j : ij ; j ∉ g_{t - 1} Тогда

α

∑ k j

k i =

j : ij ; j ∉ g_{t - 1}

1 - (1 - m_i α )

α ∑ k_j j : ij ; j ∉ g_{t - 1}

m i α

Для оценки траектории сходимости перепишем уравнение (16)

α ∑kj  α ∑kj ki = (1-miα)t ⋅ (ki -   j:ij;j∉gt-1 )+   j:ij; j∉gt-1 . (19)

^{t                  0} m_i α          m_i α

В случае, если (1 - m а) < 1 1, тогда при i α ∑kj t → ∞, (1 - miα)t → 0, а ki → j:ij; j∉gt-1 , то есть к t      miα своему устойчивому состоянию. При

(1 - m_i α ) ≥ 1 – сходимость не наблюдается.

В нашем примере (1 – m_i α) < 1 = 1 –

– 1 · 0,1 = 0,9, α ∑kj = 0,1⋅50 = 5. Однако для изначальных знаjч:ijе; jн∉gиt-1й теперь примем их уровень индивидуальных знаний после обмена в рамках группы исследователей, а именно: kА = 44,5, kБ = 30,5, kВ = 20 (данные предпо- ложения создают условия для использования формулы(15)). Если на каждом этапе в группу будет добавляться вершина с запасом знаний в объеме 50 единиц, тогда устойчивым α ∑k j5

состоянием будет k_i = ^{j : ij ; j ∉ gt - 1} =    = 50 .

m_i α     0,1

Вершина А придет к такому состоянию через 23 этапа, Б – через 35 этапов, В – 39 этапов.

В случае присоединения двух авторов с суммарным уровнем индивидуальных знаний в количестве 90 единиц устойчивое состояние будет соответствовать 45 единицам, а сходимость к нему пройдет быстрее: для А – на 11 этапе, Б – 26 этапе, В – 27 этапе.

В реальной сети уровень индивидуальных знаний исследователей и их количество может меняться от этапа к этапу, что возвращает нас к разностному уравнению (13), которое является неавтономным и не предполагает существования устойчивого состояния. Для оценки возможных изменений составим аналитический рисунок, где по оси X расположим вероятность появления вершин с высоким уровнем индивидуальных знаний (ki ≥ 50), которую обозначим через pk, а по оси Y – вероятность появления большого количества вершин (более двух вершин), pn. Тогда полученное пространство можно разделить на четыре квадранта, дифференцировав значения по осям на две группы: низкая (менее 0,5) и высокая вероятность (более 0,5). Для каждого квадранта смоделируем рост группы исследователей. Как и в предыдущем рассуждении первый этап начинается со значений kА = 44,5, kБ = 30,5, kВ = 20, то есть после первичного взаимодействия. Рассмотрим 10 этапов на основе конкретных примеров, параметры вероятности для которых приведены в таблице 1, а результаты моделирования на рисунке 3.

Квадрант 1. Динамика трех вершин в части индивидуальных знаний выходит на параллельную траекторию. За десять периодов относительная позиция вершины А в части индивидуальных знаний по сравнению с нулевым этапом сократилась на 9 %, остальных – выросла.

Квадрант 2. Увеличение вероятности появления в сети большего количества вершин влияет на схождение всех трех вершин на 10 этапе практически к единой позиции по индивидуальным знаниям. Ввиду того, что индивидуальные знания вершины А сократились более значительно, чем в предыдущем квадранте, а остальных вершин претерпели схожие изменения, лидерство вершины А практически прекратилось.

Квадрант 3. Динамика схожа с квадрантом 1, однако увеличение вероятности появления вершин с объемом индивидуальных знаний более 50 единиц позволяет вершине даже с самым высоким уровнем индивидуальных знаний улучшить свою позицию на 115 %.

Квадрант 4. В данном случае траектория, как и в квадранте 2 близка к сходимости к единой точке на 10 этапе, однако сам накопительный уровень индивидуальных знаний выше.

В результате свойственная для первого и второго квадрантов ситуация выравнивания относительной позиции исследователей с изначально более значительным уровнем

Таблица 1. Результаты изменения уровня индивидуальных знаний

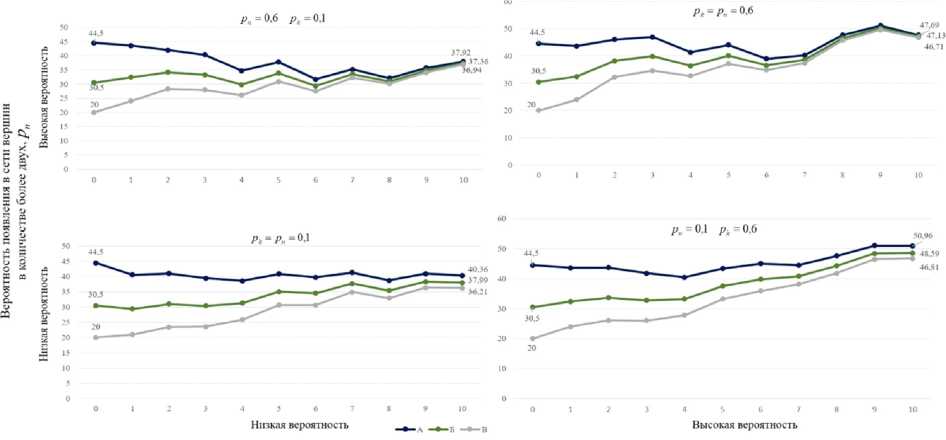
Вероятность появления в сети вершин с высоким уровнем индивидуальных знаний (более 50 единиц). р_к

Рис. 3. Динамика относительной позиции по индивидуальным знаниям с учетом неопределенности в характеристиках новых вершин

Fig. 3. Dynamics of the relative position in individual knowledge, considering the uncertainty in the characteristics of new nodes

Table 1. Results of changes in the individual knowledge level

Вершина	Прирост индивидуальных знаний по квадрантам, %
	1	2	3                1	4
	Параметры примера
	p k = p n = 0,1	p k = 0,1, p n = 0,6	p k = 0,6, p n = 0,1	p k = p n = 0,6
А	–9	–15	+15	+7
Б	+25	+22	+59	+55
В	+81	+85	+134	+134

Примечание. Рассчитано автором.

Примечание. Рассчитано автором.

индивидуальных знаний будет тяготеть к инициированию ими самостоятельных групп (рис. 4). В третьем и четвертом квадрантах такие же инициативы могут взять на себя вершины с изначально более низким уровнем индивидуальных знаний ввиду того, что они становятся более независимыми в части обладания знаниями.

С другой стороны, вполне вероятно, что группы исследователей, которые будут попадать в ситуации первого и третьего квадрантов, будут иметь более длительный рост, второго и четвертого – более короткий.

Интерпретация полученных результатов для исследования науки в городах требует выявления ориентиров, которые помогут определить свойственную для определенного города вероятность появления исследователей с относительно более значительной позицией по индивидуальным знаниям, а также вероятность поэтапного обновления группы за счет более чем двух вершин.

Обе вероятности связаны либо с миграцией исследователей из города в город, либо с внутренним формированием такого исследователя. При этом первая вероятность должна основываться на данных, которые могут дифференцировать нового исследователя по уровню индивидуальных знаний, вторая – на данных, которые могут описать способность города постоянно привлекать нескольких исследователей. Поэтому считаем, что внутренний кадровый потенциал лучше описывает вероятность pk, а миграция – pn.

Внутренний кадровый потенциал можно условно разделить на существующих и потенциальных исследователей, где первые описываются через обладание учеными степенями и выполнение научных исследований, а вторые – через численность студентов в целом или по определенным специальностям, а также обучающихся, вовлеченных в научно-техническое творчество [Кузнецова, 2023]. Данные мониторингов позволяют выявить количество студентов среднего специального (далее – СПО) и высшего образования (далее – ВО) в разрезе городов [Мониторинг деятельности … ; Мониторинг качества …]. Тогда для анализа возьмем соотношение суммарного количества студентов СПО и ВО на 1 тысячу жителей города.

Трудовая миграция может определяться широким набором факторов, среди которых особо выделяют уровень и качество жизни, а

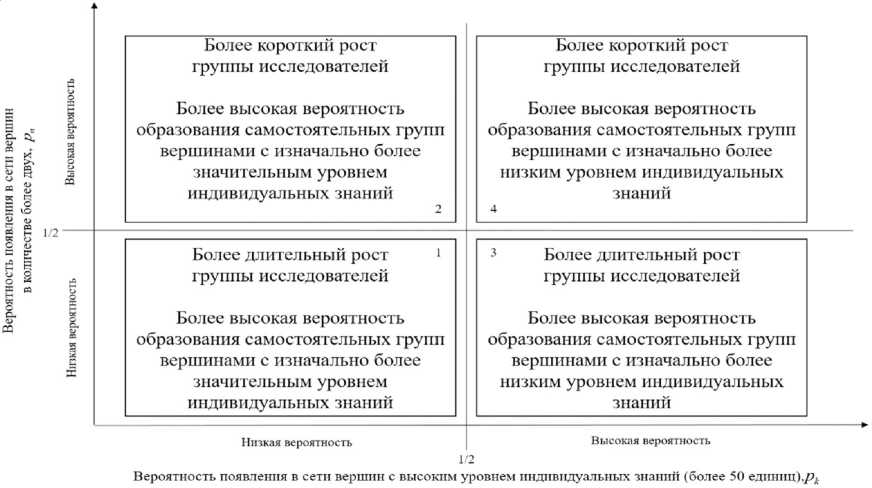
Рис. 4. Различия в росте сети локализации знаний с учетом неопределенности в характеристиках новых вершин

Fig. 4. Differences in the growth of the knowledge localization network, considering the uncertainty in the characteristics of new nodes

Примечание. Составлено автором.

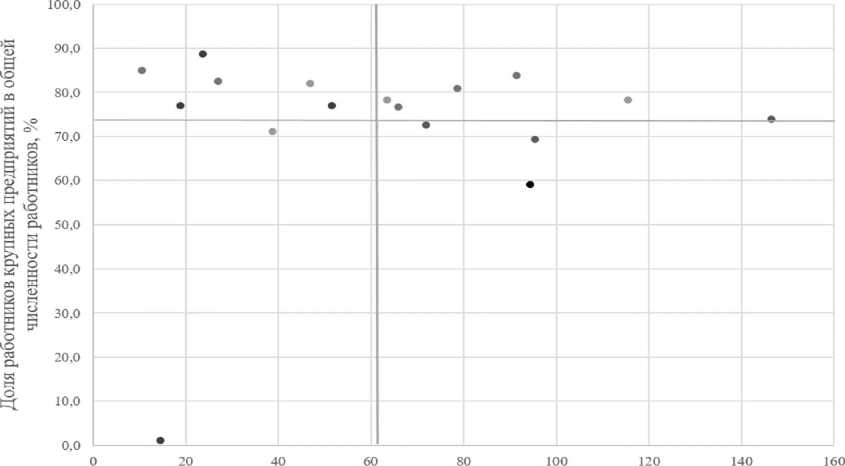
также отраслевую структуру экономики принимающей территории [Единак и др., 2023]. Научная миграция определяется в целом теми же факторами, но, кроме того, ориентируется на объем расходов на науку и исследовательскую инфраструктуру [Судакова и др., 2021]. Однако подобные факторы имеют ряд ограничений. Так, расходы на науку статистически не фиксируются на уровне городов. Ряд показателей, связанных с уровнем жизни в городах, выражены через фонд заработной платы, который дает погрешность по причине более высоких значений для территорий с особыми географическими условиями проживания. Поэтому, наиболее уместным будет считаться показатель «доля работников крупных предприятий в общей численности работников» (не исключая наличия недостатков). Построен показатель на данных Индекса качества жизни в городах России как результат вычета из 100 % показателя «отношение среднесписочной численности малых и средних пред- приятий, включая ИП, к числу занятых, %» [Индекс качества …].

Для выявление общих тенденций возьмем 17 городов, в том числе по четыре малых и больших города, пять средних, три крупных и один крупнейший. Линией разделения по оси Y и по оси X выбрано среднее значение. Результаты представлены на рисунке 5.

Малые города. Ввиду того, что собственных выпускников учебных заведений недостаточно (особенно, с учетом отсутствия во многих из них организаций ВО), то есть тех, кто выходит на более высокий уровень индивидуальных знаний, города будут тяготеть к первому и второму квадрантам рисунка 3. Города, связанные с крупными предприятиями (которых большинство), способны пополнять группы исследователей за счет более, чем двух вершин за этап.

Средние и большие города. Значительная дифференциация в части возможностей учебных заведений формирует условия для

Численность студентов ВО и СПО на 1 тыс. жителей, чел.

Рис. 5. Распределение городов на основе соотношения численности студентов и доли работников крупных предприятий

Fig. 5. Distribution of cities based on the ratio of the number of students and the proportion of employees of large enterprises

Примечание. Составлено по: [Мониторинг деятельности … ; Мониторинг качества … ; Индекс качества…]. Малый город – красный цвет кружка; средний город – зеленый; большой город – оранжевый; крупный город – синий; крупнейший город – черный.

Note. Compiled based on [Monitoring deyatelnosti … ; Monitoring kachestva … ; Indeks kachestva …]. Small city – red, medium city – green, large city – orange, very large city – blue, largest city – black circle.

присутствия городов как с низким p_k , так и с высоким. Равно как и в малых городах, в средних и больших городах в большей степени присутствуют крупные предприятия, которые облают большим набором новых рабочих мест. Соответственно, средние и большие города будут находится во втором и четвертом квадрантах, что предполагает более короткий рост групп исследователей. Вместе с тем по причине большей численности населения, отдельные большие города могут располагаться в первом квадранте, обеспечивая более длительный рост групп исследователей.

Крупные и крупнейшие города. Широкая отраслевая специализация (особенно крупнейших городов) создает предпосылки для снижения доли работников крупных предприятий, а значительное количество учебных заведений повышает вероятность появления исследователей с более высоким уровнем индивидуальных знаний, поэтому ситуация в данных городах будет приближаться, преимущественно, к третьему квадранту.

Выводы

Рассматривая сеть локализации знаний сквозь призму несвязного множества групп исследователей, автор обосновывает теоретико-игровой механизм роста таких групп. В отличие от моделей растущих сетей решение о возможном расширении группы за счет нового исследователя принимается внутри самой группы. В основу правила формирования ребра заложены два процесса: изменение индивидуальных знаний исследователя и приобретение совместных знаний в результате командной работы над научной темой. Ввиду их разного влияния предлагается параллельная реализация двух игр, которые порождают два множества равновесий по Нэшу, пересечение или объединение которых позволяет определить возможную динамику сети.

Оценка траектории относительной позиции исследователей по индивидуальным знаниям через построение разностного уравнения выявила две закономерности. Вероятность появления новых исследователей с более высоким уровнем индивидуальных знаний будет влиять на то, кто возглавит отделившиеся группы, а вероятность появления большего количества новых исследователей – на длительность роста группы.

Полученные результаты позволяют выполнить моделирование локализации знаний в зависимости от масштаба города. Для малого города несвязные компоненты сети локализации знаний преимущественно будут тяготеть к более короткому росту с периодическим выделением самостоятельных групп под руководством исследователей с изначально более высоким уровнем индивидуальных знаний. Для средних и больших городов модель должна предполагать возможное лидерство исследователей с первоначально более низким уровнем индивидуальных знаний. Для крупных и крупнейших городов моделирование требует учета большей длительности роста групп исследователей.