Модель хиггсовской инфляции и наблюдательные данные

Экспериментальное открытие бозона Хиггса в 2012 году в Большом адронном коллайдере изменило ситуацию, связанную с инфляционной космологией. Это открытие дало мощный толчок развитию теории хиггсовской инфляции. Стандартная модель хиггсовского бозона в космологии при рассмотрении космологической инфляции ранней Вселенной была впервые предложена в работе [1]. В этой работе рассматривался скалярный сектор Стандартной модели физики элементарных частиц, взаимодействующей с гравитацией неминимальным образом. В настоящей работе мы возвращаемся к первоисточнику теории инфлантона как хиггсовского бозона [1] с целью внесения уточнений на основе современных достижений теории космологической инфляции.

1.    Хиггсовская инфляция в картине Йордана в режиме медленного скатывания

В работе [1] рассматривается модель гравитации с неминимальным взаимодействием со скалярным полем Хиггса

Sj = / d⁴x^—g

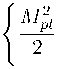
ғ (ОМ + з ( 0 ) х - м 。)}

(1.1)

• ¹ E-mail: bolshakova.ktrn@gmail.com

• ²E-mail: chervon.sergey@gmail.com

где

F (。) = - "       ， 3 = ^-1, X = -¹ 6, 帥 ," g"" ， V( 。) = ] ( 。 ² - 0²)² •          (1.2)

'%/                      2                   4

В настоящей работе, используется сигнатура (—+ ++) чтобы адаптировать действие к представленному в работе [2]. В действии (1.1) поле ф отождествляется с полем Хиггса Һ.

Уравнения космологической динамики для действия (1.1) на основе уравнений (5)-(7) работы [2] в режиме медленного скатывания ф2 t 0, фф t 0 принимают вид:

3('2 + €Ф2)Я2 + 3Н(2£фф) - 4 (ф2 - 02)2 = 0,

3(М ² + еф² )н² + 2Н (2^фф) + 2('² + (ф²) 方 —V (ф) = 0.

Вычитая (1.4) из (1.3) и интегрируя полученное уравнение, находим решение (анзац)

Н = Н₀Ф, Ф = ， '² + (ф² •

(1.3)

(1-4)

(1.5)

Для расчета космологических параметров модели определим вид первых двух параметров медленного скатывания [3]. С учетом найденного вида параметра Хаббла (1.5), параметры медленного скатывания примут следующий вид:

е

Н

Н2

НоФ2 '°

Н 2НН

Ф

2НоФФ

•

(1.6)

При ускоренном расширении вселенной е 《 1, при завершении инфляции е =1. Для рассматриваемой модели космологические параметры принимают вид:

	—2Н2 — 2Hl2Ф2       1 Н 、 2_  Н3Ф4 т =2* = 亓 2  ‘ s = 2е  2 亓    =  8*Ф ‘
2е пт= 1 - е =	2 巾                       4 巾 2 — W 帀             16 巾 二-------- ., ① -1 = -4е + 2° = ------- , r = 16е = - -6—.       (1.7 ) Н0Ф2 + Ф                    Но Ф2Ф             НоФ2

Согласно ограничениям, полученными при наблюдении анизотропии и поляризации реликтового излучения:

P_s = 2.1 • 10^-9' 九 s = 0.9663 土 0.0041, r< 0.032.

(1-8)

Условно ФН0 < -30, 9928 • 10-20 выполняется за счет выбора Но, тогда спектральный индекс находится как:

几 s - 1

-0, 25r —

4, 7077 • 10-6

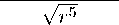
(1-9)

В этом случае при спектральном индексе 几 s = 0 . 9663 тензорно-скалярное отношение будет иметь ： зііачеіше r = 0.032. что соответствует наблтодателыіым данным.

2.    Слабое поле Хиггса в картине Эйнштейна

Действие (1.1) с помощью конформных преобразований 行 丛“ =Q²g_M " , Q² = 1 + ^- приводится к действию в картине Эйнштейна:

S e

/心

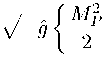
R + з(ф)Х - VE(ф) 卜

(2.1)

Здесь R- скалярная кривизна при переходе в картину Эйнштейна, ® = 1, X = -2х,нХ ,“ 0 丛"・ При этом потенциал имеет вид

Ve = АV(0) = А4 (/—「J.(2.2)

Уравнения, описывающие космологическую динамику, принимают вид:

3М|Я2 - з(ф)Х(0) - Ve(0) = 0,(2.3)

3М|Я2 + 2呼 Я + ^(ф)Х (ф) -Ve (ф) = 0.(2.4)

При этом разность и сумма уравнений (2.3) - (2.4) дает:

М*Я = -^Х (ф), Ve (ф) = М| (3Я2 + Я).(2.5)

Для слабого поля Хиггса, как отмечается в работе [1], һ = ф t х, Q² — 1. В этом случае действие (1.1) и (2.1) совпадают и можно найти точное решение с использованием генерирующий функции для полиномиальных потенциалов [3]. Как показано в монографии [3], выбор генерирующей функции 巧 еп, зависящей от скалярного поля ф произвольным образом, позволяет определить параметр Хиггса Я(ф) ii потенциал V (ф) с, 「 едутош,ті образом

я(ф) = М^Ғдеп, V(ф) = 3М/Я2 - 2Ml (臨/ = -2Ml (^,了 + 俨…⑹十尸»2 ,仁⑹ где %еп некоторая постоянная. Генерирующая функция вида

^Ғдеп = Ao + 入 20², 入 0 = ],入 2 =                              ( 2.7)

払 2

приводит к точному решению при ограничении на вакуумное среднее хиггсовского поля 。：。 = ^|р

Решение имеет следующий вид:

ф ⑴ =фо exp

(Y о

М)=2 Т! ф0exp (Y ^+6 Т!.

(2-8)

Оценим второе слагаемое параметра Хаббла в (2.8) 6 、/鼻

^10-13 仁 1, 83 • 10^-7. В виду ого

малости этим слагаемым можно пренебречь. Тогда параметр Хаббла будет иметь вид с учетом

^замены В = 、/ 1

10-13

Я ⑴ =2вф0 exp (-44)

(2.9)

Найдем число е-увеличений ^:

(2.10)

N = - — ф0 exp(-4В 。 + N*, 8

где N* = cons^ константа ііптегрііроваіііія. Параметры медленного скатывания ：

d 1пЯ (N ) dN

¹           ₌ — ^{1 d 1}n e =      ³

N -N*,  ( 丿— ^e - 2 IN = 2(N -N*).

(2.11)

Для данной модели спектральный индекс принимает вид ns - 1

-4e + 2b

N -N*.

(2.12)

При N = 60 ii n_s — 1 = -0, 0337 получаем

N* = 30, 3264, e(N) = 0, 0337

(2.13)

Найдем зависимость r(n_s)

『 Ss) = Т- 1 ) .                             (2.14)

Для максимального значения скалярного спектрального индекса п* 。 " = 0, 97 тензорно-скалярное отношение будет иметь значение r*2n = 0, 04, что близко подходит, но, строго говоря, не соответствует наблюдательным ограничениям.

Заключение

В работе показано, что хиггсовская инфляционная модель имеет некоторые дополнительные решения в картине Йордана и в картине Эйнштейна в режиме медленного скатывания и для слабого хиггсовского поля. В картине Йордана решения соответствуют наблюдательным данным. Для картины Эйнштейна полученные решения в случае слабого поля, строго говоря, не согласуются с наблюдательными данными. В дальнейшем планируется скорректировать эту модель с учетом квантовых поправок за счет слагаемого Гаусса-Бонне в исходном действии.