Модель и алгоритм оптимизации планировочных решений на градостроительных территориях

В последнее время чрезвычайно выросли сложность и комплексность проблем, возникающих в процессе принятия управленческих реше- ний в практике планирования градостроительства [1; 11-13]. Одна из трудностей принятия решений состоит в необходимости учета большого количества противоречивых критериев [1; 13]. Вторая трудность связана с высокой степенью неопределенности, обусловленной недостаточным уровнем информации для принятия обоснованных решений [12].

В связи с постоянным ростом сложности задач, возникающих в современном градостроительстве, традиционные методы их решений оказываются малоэффективными. Практика показывает, что если управленческие структуры, принимающие решения, опираются только на собственный опыт, то они часто принимают ошибочные решения, которые приводят к фатальным последствиям [11; 13]. В настоящей статье рассмотрим задачу построения модели и алгоритма оптимизации планировочных решений применительно к градостроительной системе населенного пункта (ГСНП).

Планирование застройки территории как линейная задача синтеза сетевой структуры коммуникационного типа

Пусть задан ориентированныйграф с вершинами из множества P = { p i : i = 1, Л } и дугами j, принадлежащими множеству { G }. Рассмотрим также некоторую совокупность вершин { A } (подмножество множества P ) A = { p i : i = 1, n } , которые будем называть источниками (первоначальными, или изначально планируемыми местами расположения зданий и сооружений на территории ГСНП). Будем считать выполненным свойство i е A ^ D ( i ) = { 0 } , т.е. из вершин-источников дуги только выходят [2].

Рассмотрим та кже некот орое множество вершин С = { p i : i = Л - m + 1, Л } , которые назовем стоками (новыми, или скорректированными местами расположения зданий и сооружений на территории ГСНП) и для которых предполагается свойство i е C ^ C ( i ) = { 0 } , т.е. в вершины-стоки дуги только входят. Пусть остав шиеся верш ины образуют множество B = { p i : i = n + 1, Л - m } , которые будем называть промежуточными вершинами (или местами возможного расположения зданий и сооружений на территории ГСНП).

Пусть каждой вершине p i е A поставлена в соответствие некоторая неотрицательная функция ф(x ) >  0 ( x е X ), где X - множество, включающее в себя подмножества строительных, энергетических, людских ресурсов, а также риск-состояний в вершинах (фактически в пределах элементарных площадок-таксонов), зависящих от величин рисков, исходящих от геологической среды и гидрологической сети (или, выражаясь языком задач оптимального распределения ресурсов на коммуникационных сетях, множество допустимых распределений ресурсов).

Кроме того, известны неотрицательные функции фJ (x) > 0 , задающие пропускные способности дуг сети в зависимости от выбранного распределения ресурсов. Таким образом, ресурсы распределены как между вершинами-источниками, определяя тем самым мощности источников, так и между дугами сети, определяя их пропускные способности. Для вершин-стоков известны величины минимальных риск-состояний, являющихся безопасными для зданий и сооружений ГСНП, т.е. известны потребности этих вершин-стоков (элементарных участков-таксонов) в зданиях и сооружениях. Обозначим их через Zj. Таким образом, формально задача состоит в рассмотрении допустимых распределений по территории ГСНП зданий и сооружений по отдельным элементарным участкам-таксонам и связанных с ними допустимых потоков (перемещений, или изменений мест расположения зданий и сооружений), которые за счет опасных (или повышенных) значений риск-состояний в источниках удовлетворяют перемещению зданий и сооружений на участки-таксоны с безопасными значениями риск-состояний в стоках сети. Математическая запись ограничений на допустимость потока будет выглядеть следующим образом [16]:

Е yj - T i⁽x ), P i ^e A , E yj - Zi ’ P i ^{G C} , j ^{e C} (‘ )                                     j ^e D ⁽‘ )

E y j - E y j = ⁰, P i ^{e B} , x ^e X;

j ^e C ( i )         j ^e D ( i )

0 - y j - T j ( X ); j e G.                     ⁽¹⁾

Если теперь ввести функцию f ( x ) как функцию, характеризующую оптимальность изменения мест расположения зданий и сооружений по территории ГСНП (или стоимость распределения ресурсов) и рассматривать при этом однородный сепарабельный процесс, то функция f ( x ) будет определяться количеством ресурса, выделяемого из вершины-источника x i ( p i е A ) и дуги сети x j ( j е G ). Функцию f ( x ) в таком случае будем представлять в следующем виде: f ( x ) = Е x + Е x j ; x > 0; ^x j > ⁰; p i ^е A ;

p е A     j еС j е G,                                          (2)

и далее для решения нашей задачи необходимо рассматривать минимизацию функции (2) при ограничениях (1).

Такой качественно новый подход к проблеме планирования застройки территорий градостроительных систем населенных пунктов, по нашему мнению, должен являться базовой основой, необходимой для разработки моделей и алгоритмов управления развитием ГСНП с целью принятия управленческими структурами обоснованных градостроительных решений.

Формализованное представление ресурсов сетевой структуры градостроительной системы населенного пункта

Как уже указано, под ресурсами в отношении решения нашей проблемы по управлению развитием ГСНП понимается совокупность строи-

ВЕСТНИК 2015

ВЕСТНИК 2015

тельных, энергетических, людских ресурсов, а также риск-состояния территории ГСНП, осред-ненные по элементарным участкам-таксонам, на которые разбита территория ГСНП. Несколько расширим теперь рамки понимания ресурсов с точки зрения рассматриваемой в настоящей работе проблемы.

Определим для каждого элементарного участка-таксона, на которые разбита исследуемая территория ГСНП, некотор ое непу ст ое множество ресурсов X_t = { х , : i = 1, n ; z = 1, d } , где d – количество возможных способов оценки ресурсов для каждого элементарного участка-таксона; n – количество элементарных участков-таксонов, которые полностью четко покрывают рассматриваемую территорию ГСНП. В таком случае каждый из элементов x i е X i будет представлять собой объект достаточно сложной структуры.

Действительно, во-первых, каждый элементарный участок-таксон характеризуется его г ео -динамическим риск-состоянием g^k е G ( i = 1, n , k = 1, m ), которые известны по оценкам, полученным ранее из различных источников (как экспертных, так и на основании данных математического моделирования). Геодинамические риск-состояния определяются следующим набором свойств: g_i ¹ – «оползневые процессы»; g_i ² – «просадочные процессы»; g_i ³ – «карстовообвальные процессы»; g_i ⁴ – «деформационные процессы»; g_i ⁵ – «градиентность топографического рельефа местности» [3–10; 14; 15; 17].

Во-вторых, риск-состояние элементарного участка-таксона определяется не только его гео-динамическим состоянием, но и наличием или отсутствием в его пределах гидрологичес ко й, либо_гидрогеологической сети ri' е R ( i = 1, n , j = 1, c ). Эти риски определяются следующими свойствами: r_i ¹ – «риски гидрологической сети»; r_i ² – «риски гидрогеологической сети»; r_i ³ – «риски морфоструктурных линеаментов»; r_i ⁴– «риски трещиноватости геологической среды» [3–10; 14; 15; 17].

Далее, каждый из элементарных участков-таксонов может либо содержать, либо не содержать планируемое место размещения здания или сооружения (далее СО – строительного объекта). То есть, каждый участок-таксон будет характеризоваться свойствами СО или группы таких объектов. Также будем предполагать для упрощения формализации нашей задачи, что в пределах одного таксона может располагаться единственный СО со своими свойствами s i е S ( i = 1, n ; p = 1, l ).

Определимся теперь со свойствами СО. Такими свойствами будут: s ¹ – «строительные ₂ i                                    ₃

ресурсы»; s_i ² – «энергетические ресурсы»; s_i ³ – «коммуникационные (транспортные) ресурсы; s_i ⁴ – «людские ресурсы».

Далее, поскольку наличие или отсутствие СО в пределах элементарного участка-таксона характеризует его свободность или занятость в случае изменения места расположения СО из какого-либо другого участка-таксона, необходимо ввести такую характеристику элемента x_i , как его пригодность для перемещения СО b q е B ( i = 1, n , q = 1, t ). Свойствами этой характеристики будут следующие: b_i ¹ – «занятость другим СО»; b_i ² – «медико-биологическая привлекательность территории для строительства»; b_i ³ – «психолого-эстетическая привлекательность территории для строительства» [3].

Таким образом, с формальной точки зрения при описании ресурсов для каждого элементарного участка-таксона в данном случае мы можем оперировать с элементами некоторого непустого множества ^х , = { x i ^: x = ( g k , ri , s i , b q ) } ( i = 1, n ; k = 1, m ; j = 1, c ; p = 1, l ; q = 1, t ; ^z = 1, d ).

Численно каждую из составляющих элементов множества X_i будем характеризовать величиной интенсивности проявления его свойств,

на основании которых можно рассчитать инте-

гральные характеристики элементов множества ресурсов X_i .

Рассмотрим теперь вопрос о количественной оценке элементов множества ресурсов X_i . Введем следующие обозначения:

§k, rtj , si , b/ - абсолютные интенсивности проявления свойств элементов gk е G, rj е R, si е S, bq е B ; _ g k , r j , s p , b q – относительные интенсивности проявления свойств элементов gk е G, ri е R, si е S, bq е B, определяемые соотноше-

ниями вида:

^g k *

^{b q *}

g k max j?k ^ b q maxb q

где max g ^k ,

,

r k j^:

j r j maxr j

max r ^j ,

^{p ,} s

*

s p

^, max s k i

max si i , max b q

–

макси-

мальные абсолютные интенсивности проявления свойств элементов g^k е G , ri е R , si е S , b^q е B .

Тогда интенсивность проявления свойств

элемента x i е X_t будем обозначать следующим образом: к,^z * = ^ ( ^g k * , r i j * ,•? i * , b> i * ) . Знаком суммы мы обозначаем линейную комбинацию относительных интенсивностей проявления свойств

элементов g^k е G , Г е R , s i е S , b q е B в предположении их равновесности в указанной комбинации.

Множество элементов x Z * будем называть множеством L_R . Авторами разработана аксиоматика этого множества и показано, что непустое множество L_R является абелевой группой, а совокупность непустых множеств элементов X_i (множеств ресурсов) и соответствующие им абелевы группы L_R интенсивностей проявления свойств этих элементов назовем пространством ресурсов X (не в алгебраическом смысле).

Таким образом, предложен принципиально новый подход к представлению разнородных ресурсов (ресурсов различного генезиса) сетевых структур градостроительных систем населенных пунктов, основанный на аксиоматическом задании и формализованном описании множества ресурсов. Подобное представление ресурсов в виде пространства позволяет оперировать ресурсами на языке алгебры множеств, что дает возможность количественно оценивать ресурсы для каждого элементарного участка-таксона и задавать их в сепарабельном виде.

Методика количественной оценки состояния ресурсов сетевой структуры градостроительной системы населенных пунктов

Рассмотрим методику количественной оценки ресурсов. Изложим вначале в аксиоматическом виде те упрощения, которые позволяют нам это сделать.

Аксиома 1. Отдельный элементарный участок-таксон содержит не более одного строительного элемента.

Аксиома 2. Строительные, коммуникационные, энергетические и людские ресурсы s i е S ( i = 1, n ; p = 1, l ) для каждого отдельного элементарного участка-таксона полагаются одинаковыми и равными одной относительной условной единице.

Аксиома 3. Ресурсы в пределах отдельного элементарного участка-таксона пол но стью опр еделяются элементами g^k k е G ( i = 1 , n , k = 1,m ), Г е R ( i =1_ n , j = 1 c ), b^q е B ( i = 1, n , q = 1, t ), s i е S ( i = 1, n ; p = 1, l ) при s i = const .

С этих позиций пространство ресурсов X можно рассматривать как некоторое пространство, состояние которого в каждой точке этого пространства будет зависеть от риск-состояний среды градостроительной системы населенных пунктов. В связи с этим введем следующие понятия.

Определение 1. Невозмущенным режимом функционирования пространства ресурсов X в каждом его элементарном объеме будем называть его поведение при отсутствии проявлений на территории ГСНП опасных природных и природно-техногенных процессов геодинамиче-ского происхождения. Состояние пространства X, соответствующее такому режиму его функционирования, назовем равновесным состоянием.

Определение 2. Режим функционирования пространства X в каждом его элементарном объеме в условиях проявления на территории ГСНП опасных природных и природно-техногенных процессов геодинамического происхождения будем называть возмущенным, а состояние пространства X – неравновесным состоянием.

Определение 3. Полем состояний S пространства ресурсов X назовем упорядоченную совокупность состояний S_i ( i = 1, …, n ), каждое из которых количественно характеризует величину отклонения поведения пространства X от его невозмущенного режима функционирования.

Отдельные состояния будем называть элементами поля состояний, при этом значение элемента S_i поля состояний S , соответствующего невозмущенному режиму функционирования пространства X , будем полагать величиной бесконечно малой.

Определение 4. Под масштабным параметром p будем понимать выраженную в относительных единицах линейную протяженность ГСНП вдоль приоритетного направления, т.е. того направления, вдоль которого оценивается величина определенных нами выше ресурсов для решения задачи об оптимальном размещении строительных объектов на территории ГСНП. При этом величина масштабного параметра p е [ 0; 1 ] .

Определение 5. Под интервалом характеристического времени т будем понимать период времени, на котором выполняется оценка режимов функционирования пространства X ГСНП. Будем также полагать, что значения характеристического времени т е [ 0; 1 ] .

В таком случае проекции значений поля состояний S пространства ресурсов X будем считать принадлежащими фазовому пространству ⁽ Р , ^т ).

Для количественной оценки поля состояний пространства ресурсов X градостроительной системы населенных пунктов введем следующие функции.

Определение 6. Функцией состояний W ( р ; т ) назовем функцию, определяющую в каждой точке фазового пространства ( р , т ) величину значений поля состояний пространства ресурсов X .

Определение 7. Функцией компенсации F ( р ; т ) назовем функцию, определяющую в каждой точке фазового пространства ( р , т ) из-

ВЕСТНИК 2015

менение величины значений поля состояний пространства ресурсов X, т.е. величину «возму- щения», стремящегося вернуть пространство ресурсов X в равновесное состояние.

Функцию W ( р; т ) определим как функцию, удовлетворяющую уравнению V 2 V 2 W ( р; т ) = 0, так как поле состояний является равновесной системой. Решением этого уравнения, как известно, является функция вида

W ( р ; т ) = { ( A + C t ) shk T +

+ ( B + D t ) chk T } sin( k p + ф ).

Тогда функцию F(р; т) определим на осно-— вании соотношения f(р; т) = gradw(р,т), т.е.

—

F ⁽ р ;^т) =

д W ( р , т ) Л д W ( р ,т) Л др    i ⁺    дт    j

Л Л где i, j – единичные векторы координатных осей р и т соответственно.

ВЕСТНИК 2015

В таком случае компоненты функции F ( р; т ) представляют собой:

д W ( р , т )

• 1)    функцию f_p ^{( р};^т ) =   д р   , определяе

мую как частная производная по переменной р

(масштабный параметр) на основании того, что часть компенсирующих факторов природного и антропогенного характера существенным образом зависит от морфоструктурного типа территории, особенностей ландшафта, площади территории, гидрологической и гидрогеологической сети и т.п. факторов;

д w ( р , т )

• 2)    функцию f_s ( р ; т ) =--------, определяе-

• д

мую как частная производная по переменной (характеристическое время), поскольку часть компенсирующих факторов природного и антро- погенного характера проявляется только спустя некоторое время после реализации опасного природного или природно-техногенного процесса геодинамического происхождения.

То есть, функцию f_p ( р; т ) можно определить как функцию территориальной компенсации, а функцию f s ( р; т ) можно определить как функцию временной компенсации, зависящую от времени реакции природной, техногенной и антропогенной сред на проявление опасных природных или природно-техногенных процессов геодинамического происхождения.

Тогда на основании выражений (4) и (5) компоненты функции компенсации F(р; т) будут находиться по следующим соотношениям:

( A + С т ) shk т + f_P ⁽ р, ^{т )} = ^к 1 ,        .

+ ( B + D т ) chk т

> cos( к р + ф ),

<

'[ к ( B + D т ) + С ] shk +' f S ( р , т ) = 1^L_r\     \ "

+ [ к ( A + С т ) + D J chk т

- sin( к р + ф ).   (6)

Изменение значений элементов поля состояний пространства ресурсов X в каждой точке фазового пространства ( р ; т ) будем оценивать на основании следующего соотношения:

I F ( р ,^т |=V f p ²⁽ р ,^т )⁺ f s ²⁽ р, ^ ). ⁽⁷⁾

Приведем также систему расчетных уравнений для определения функций f_p ( р ; т ) и fS ⁽ р ;^{т ):}

f s ( p , T ) = F ₀ + jr f „ sin( k p + V n ) { ( 1 + к тА - в ) shk T - ^ k r chk r } .

• ¹                  ” = 1                                                      (8)

По соотношениям системы (8) и выражению (7) были рассчитаны значения поля состояний пространства ресурсов для различных модельных видов проявлений воздействий в среде ГСНП опасных факторов геодинамического происхождения.

Фазовые диаграммы поля риск-состояний для среды ГСНП при модельных воздействиях параболического вида ф ( р ) = 1 - р ² (тип 1) и нор-

1      - мального вида ^(р) = —е=е 2ст (тип 2) приве-П дены на рис. 1 и рис. 2.

Подобная математическая технология позволяет оценить интенсивности воздействий на среду ГСНП опасных факторов геодинамического происхождения и строить распределенные фазовые диаграммы риск-состояний для множества элементарных участков-таксонов, полностью покрывающих территорию исследуемой градостроительной системы населенного пункта.

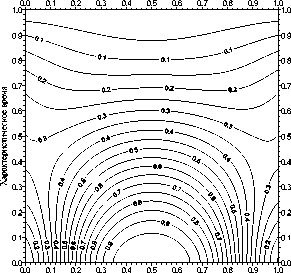
Масштабный параметр

Рис. 1. Фазовая диаграмма поля состояний пространства ресурсов (риск-состояний среды ГСНП) при модельном воздействии параболического вида (тип 1)

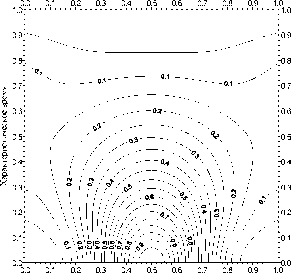
Масштабный параметр

Рис. 2. Фазовая диаграмма поля состояний пространства ресурсов (риск-состояний среды ГСНП) при модельном воздействии нормального вида (тип 2)

Процедура практического решения задачи оптимального размещения строительных объектов в рисковой зоне

Предположим, что на территории некоторой ГСНП планируется размещение некоторого множества строительных объектов (СО) O = { o h I h = 1, v } (рис. 3). При этом известны свойства этих объектов s h е S ( h = 1, v ; p = 1, l ), полностью удовлетворяющие условиям аксиом 1 и 2. Также предположим, что для участков-таксонов y_t ( i = 1, n ) известны их свойства g i е G ( i = 1, n , k = 1, m ), r е R ( i = 1, n , j = 1, c ), b q е B ( i = 1, n , q = 1, t ), полностью удовлетворяющие условиям аксиом 1 и 3. При этом полагается, что участки-таксоны полностью покрывают территорию рассматриваемой ГСНП.

Требуется: 1) определить, насколько оптимально планируемое размещение СО в пределах территории ГСНП с точки зрения их безопасности в отношении проявления рисков геодина-мической природы; 2) если ряд СО (или все СО) находятся на опасных участках, то необходимо выполнить новую планировку размещения этих строительных объектов с учетом оптимальности их перемещения на новые места.

01 23456

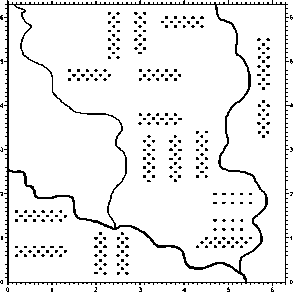
Рис. 3. Планируемое размещение строительных объектов на территории ГСНП. На рисунке схематично обозначена гидрологическая сеть. Цена единицы деления по осям координат составляет 100 м

Рассмотрим методику решения этой задачи на примере некоторого конкретного строительного объекта o t е O . В первую очередь необходимо определить положение СО в пространстве координат ГСНП. Определим это пространство как пространство U (0; X ; ф ), где X - условная долгота ( x -координата); φ – условная широта ( y -координата); 0 – начало отсчета. При этом будем полагать, что начало отсчета совмещено с левым нижним углом схемы, отображающей территорию ГСНП. Тогда его координаты будут ( λ ₀ ; φ ₀ ). Поскольку множество строительных объектов удовлетворяет условиям аксиом 1 и 2, то мы значительно упрощаем нашу задачу, полагая, что наш СО является «точечным» и принадлежащим конкретному одному определенному элементарному участку-таксону, и координаты конкретного объекта обозначим как ( λ_t ; φ_t ).

В этом случае мы будем знать свойства среды этого таксона и, соответственно, величину риска R_o для строительного объекта o t е O . Если величина этого риска R_o <  R reas ( R reas - величина допустимого риска; reasonable – «разумный»), то СО может оставаться на прежнем месте его размещения, если же R_o >  R reas , то необходимо переместить строительный объект o t е O в другую позицию на территории ГСНП.

При этом необходимо учитывать два следующих момента:

• 1)    на новом месте расположения СО (месте расположения с координатами ( X ' ; ф \ ) величина риска должна удовлетворять условию R_o , <  R_reas ;

• 2)    перемещение необходимо производить таким образом, чтобы строительный объект оказался бы на наименьшем расстоянии от предыдущего места расположения данного объекта, т.е. должно быть выполнено условие минимизации пути перемещения строительного объекта.

Опишем теперь кратко алгоритм перемещения единичного «точечного» строительного объекта o t е O .

• 1.    Выполняется оценка риска, т.е. оценка риск-состояний для каждого элементарного участка-таксона y i ( i = 1, n ) вдоль совокупности взаимно перпендикулярных профилей, на которые разбивается исследуемая территория ГСНП. Выполнение этой оценки представляет собой последовательность следующих действий.

  • 1.1.    Вводится информация по величинам д ; ^k , r j , к р , b q , являющимся составляющими элементов неп уст ого множества ресурсов X_t = { x i : i = 1, n ; z = 1, d } . При этом полагается, что величины д к ^k , r - j , s p , b iq полностью удовлетворяют условиям аксиом 2 и 3.

    ВЕСТНИК 2015

    
    

    ВЕСТНИК 2015

    
    

  • 1.2.    Определяются величины max g k , max Г , max i p , max b q .

  • 1.3.    Рассчитываются величины g k *, Г *, i p *, b_i^{q *} , определяемые по соотношениям вида (3).

  • 1.4.    Находится интенсивность проявления свойств элементов x i е X, в соответствии с со- ii

отношением вида x i = ^ l g i , Г , s ip , b q I .

• 1.5.    Вводятся линейные размеры территории ГСНП, а также временной интервал оценки состояния исследуемой территории, и на основании этого определяются масштабный параметр р и характеристическое время т .Тем самым задаются параметры фазового пространства оценки риск-состояний ( р , т ).

• 1.6.    На основе информации об интенсивности проявления свойств элементов x i е X i , соотношений (7), (8) строится фазовая диаграмма поля состояний ресурсов (риск-состояний среды ГСНП) при воздействии на пространство ресурсов X , определяемое интенсивностями проявления свойств элементов x i е X i .

• 1.7.    Выполняется обратный переход к линейным размерам территории на основе объединения информации по риск-состояниям для отдельных элементарных участков-таксонов.

• 2.    Проверка безопасности планируемого места расположения строительного объекта. Такая проверка, как мы уже указывали выше, выполняется на основании соотношения R o <  R_reas , где R_reas – величина допустимого риска, которая задается в ходе реализации алгоритма. Если это условие выполняется, то строительный объект остается на прежнем месте его размещения и работа алгоритма для данного объекта на этом завершается, если же R o >  R_reas , то строительный объект необходимо переместить в другую позицию на территории ГСНП, т.е. алгоритм переходит к следующему этапу его реализации (при множестве объектов, требуемых к перемещению, формируется массив таких строительных объектов O_n ).

• 3.    Выборка безопасного с точки зрения риск-состояний элементарного участка-таксона, предполагаемого для нового места размещения строительного объекта. Этот этап также реализуется в виде следующей последовательности действий.

• 4.    Выполняется анализ массива участков-таксонов 11 1^^ 11 (массив, в который включаются участки-таксоны, которые могут быть занятыми перемещенным строительным объектом) на предмет определения таксона, находящегося на минимальном расстоянии от предыдущего места расположения строительного объекта, т.е. фактически этап 3 и этап 4 представляют собой прак-

• тическую реализацию линейных задач синтеза сетевой структуры коммуникационного типа вида. Если данная задача решается для одного конкретного СО, то алгоритм завершается, если же он реализуется для некоторого множества СО, то переходим к выполнению следующего, последнего, этапа.

• 5.    Формируем массив участков-таксонов ||У ^|, в который включаются участки-таксоны, занятые перемещенными строительными объектами, и массив координат перемещенных СО ||О /||, и переходим к выполнению п. 2.

После исчерпания множества строительных объектов работа алгоритма завершается, и данные записываются в выходной файл в виде координат новых мест размещения строительных объектов, который затем графически интерпретируется в виде карты-схемы оптимизации размещения СО.

Таким образом, пространство ресурсов X , поле его состояний S , набор соотношений (1) – (3), (7), (8), а также совокупность соответствующих им аксиом, правил и условий их обработки, назовем моделью оптимизации размещения строительных объектов на территории градостроительной системы населенных пунктов , а последовательность и правила практической реализации этой модели, изложенные выше, назовем алгоритмом оптимизации размещения строительных объектов на территории градостроительной системы населенных пунктов.

Приведем теперь конкретный пример практической реализации модели и алгоритма оптимизации размещения строительных объектов на территории градостроительной системы населенных пунктов, представленной на рис. 3.

В ходе реализации п. 1 алгоритма оптимизации размещения строительных объектов на территории данной ГСНП была выполнена оценка риск-состояния среды этой системы (рис. 4). Затем была выполнена проверка безопасности планируемых мест расположения строительных объектов на территории исследуемой модельной ГСНП при принятом значении допустимого риска R_reas = 0,75. То есть, при значениях риска R o >  0,75 строительный объект должен быть перемещен на новое, более безопасное место его расположения, туда, где в данном случае R_o < 0,75. Результаты такой проверки приведены на рис. 5.

Как видно из данных, представленных на рис. 5, запланированные места расположения 40 из 274 строительных объектов находятся на участках со значениями риска, превышающими допустимую величину в 0,75.

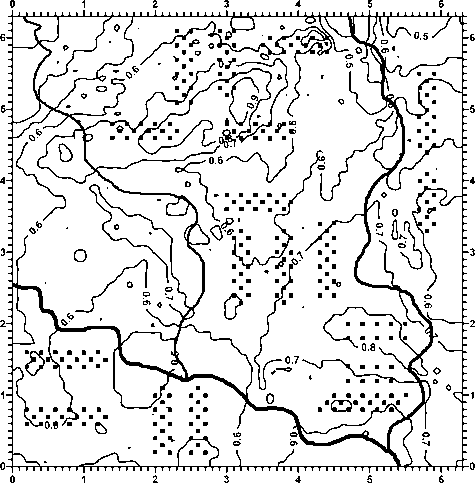
Рис. 4. Эквипотенциальное распределение величин риск-состояния для среды модельной ГСНП. Дискретизация изолиний 0,1

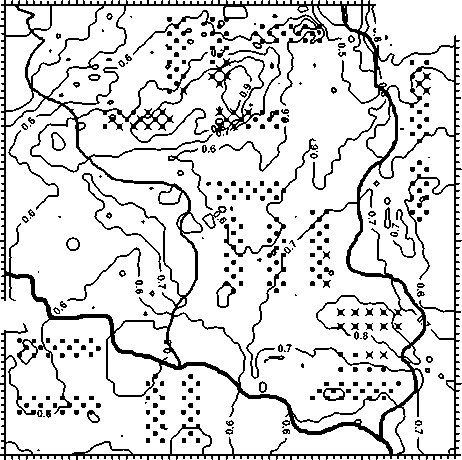
Рис. 5. Результаты проверки безопасности планируемых мест расположения строительных объектов на территории исследуемой модельной ГСНП при принятом значении допустимого риска R _reas = 0,75. Крестиками обозначены СО, находящиеся в местах повышенного риска

Представим теперь карту-схему оптимального размещения строительных объектов на территории ГСНП, на которой обозначены новые места перемещенных СО после реализации остальных пунктов рассмотренного выше алгоритма (рис. 6).

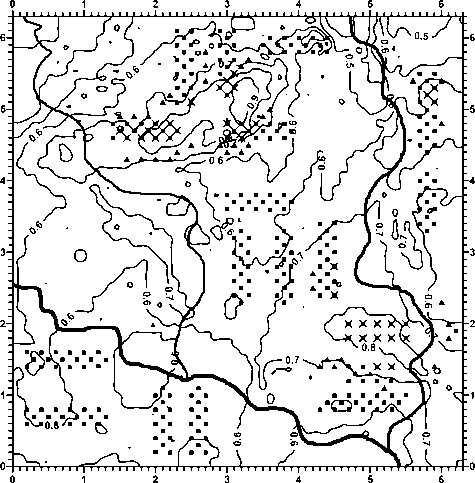
Рис. 6. Карта-схема оптимального размещения строительных объектов на территории ГСНП. Треугольниками обозначены новые места расположения перемещенных строительных объектов

Заключение

Задачи принятия управленческих решений в практике планирования градостроительства отличаются существенной сложностью и комплексностью. В работе показано, что для оптимизации планировочных решений целесообразно применять понятийный и математический аппарат моделирования оптимальной застройки территории и последующего решения линейной задачи синтеза сетевой структуры коммуникационного типа. При этом необходимо учитывать ресурсы сетевой структуры градостроительной системы населенного пункта на основе их формализованного описания. Пошаговая процедура практической реализации оптимального размещения строительных объектов, описанная в статье, использует такую количественную оценку состояния ресурсов.

Как следует из рис. 6, все перемещенные на новые места СО оказались на участках территории ГСНП, где величина риска меньше допустимого значения, что подтверждает работоспособность модели и соответствующего ей алгоритма оптимизации и достоверность полученных результатов по размещению строительных объектов на территории градостроительства.

ВЕСТНИК 2015