Модель и алгоритмы оптимизации сети передачи данных

В традиционных постановках задач оптимизации сети передачи информации (СПД) результативность проектного решения принято оценивать исходя из значения критерия, на который оказывает влияние объем переданной информации или величина задержки пакета. По причине изменения технических свойств сетей (применение широкополосных каналов связи) возникла необходимость развития моделей и методов оптимизации СПД [6]. Подобный переход касается потребности корректного математического описания реальных объектов, а также требований экономического характера.

Важной задачей управления СПД на сетевом уровне является управление маршрутизацией пакетов [1]. Данная методика позволяет оптимизировать СПД по единому принци-

• 4 т елекоммуникационные системы

пу с учетом вероятностно-временных характеристик передачи информационных пакетов, а также распределения информационных потоков и формирования на их основе системы маршрутных таблиц [8] без учета специфики построения беспроводной транспортной сети связи. Вышесказанное позволяет сделать вывод об актуальности рассматриваемой темы.

Математическая модель сети передачи данных

Основой предлагаемой модели сети передачи данных являются традиционные потоковые модели [7]. Известен ориентированный ациклический граф G = ( V,E ), который характеризует текущую сеть, пример которой отражен на рисунке.

V является множеством вершин, которым соответствуют коммутаторы, являющиеся узловыми компонентами сети [5]. Ребро ( u,v ) ∈ E между вершинами u и v задает канал связи, обладая положительной пропускной способностью c ( u , v ), а также отражает максимально возможный объем данных, который может быть передан посредством него за единицу времени.

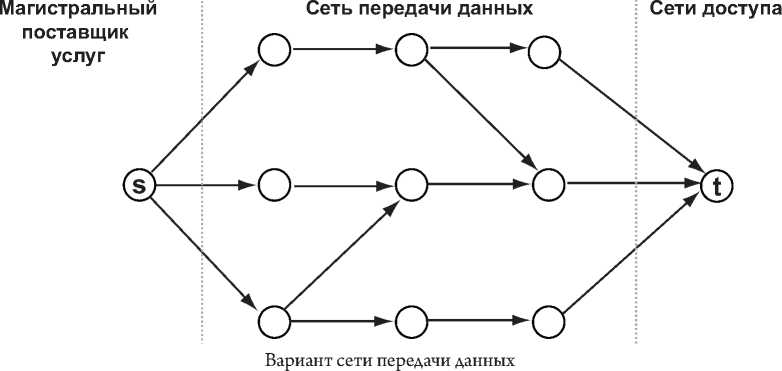
На рисунке наглядно представлен граф с двумя вершинами, среди которых источник информации s и сток t. Из s идут каналы от магистрального оператора, которые соединяют сеть регионального ISP с сетями доступа. В сток идут ребра от коммутаторов с подключенными к ним сетями доступа.

Множество ребер E ′ ( E ∩ E ′ = Ø) характеризует все каналы передачи данных, которые могут быть достроены. Для каждого ( u,v ) ∈ E ′ обозначена пропускная способность c ′( u,v ) и стоимость построения p′{u, v).

Проведем нумерацию всех ребер из множеств E ′ произвольным образом разными целыми числами от 1 до |E′|, приняв обозначение e_i для ребра под номером i из E′. Моделирование транспортировки данных в сети происходит посредством функции потока:

f_G : V x V ^ R , (1) где x - декартово произведение; R - множество вещественных чисел.

Модель и алгоритмы оптимизации сети передачи данных

Величина f_G ( u , v ) отражает объем данных, который передается за единицу времени по каналу связи определенного ребра между вершинами u и v . Функция f_G удовлетворяет ряду условий, среди которых:

1)    лимит пропускной способности: ∀u,ν∈V: fG(u,ν) ≤ c(u,ν); 2)    антисимметричность: ∀u,ν ∈ V : fG(u,v) = - fG (ν,u); 3)    сохранение потока: Vu е V \ {s, t}: ^v V f (u, v) = 0.

Через | f_G | обозначим величину потока в графе G, который отражает возможный объем данных, переданных из источника в сток за единицу времени. В этом случае | f_G | можно рассчитать посредством формулы

IЛ| = £v Jg (s, v)

Через |FG| принимаем обозначение максимальной величины потока в графе G среди возможных значений fG. Планом проектирования сети передачи данных является множество ребер Е* ∈ E', отвечающее каналам связи, которые будут достроены. В ходе принятия решения о реализации плана проектирования исходная сеть подвергается трансформации в сеть, которая характеризуется графом G* = (V,E ∪ E*).

Стоимость построения равна

У, ,. 2-^ ( u, v )е E

p‘(u, v). При этом величина максимальной про- пускной способности – |FG*|. Важно обратить внимание, что рассмотренная выше математическая модель применима ко многим предметным областям, где затрагивается опти- мизация структуры сетей разной природы.

Задача оптимизации сети передачи данных

Исходя из заданных ациклических ориентированных графов G = ( V , E ) и множества ребер Е'(Е ∩ Е' = ∅ ), матриц пропускных способностей c ( u,ν ) и c' ( u,ν ), а также матрицы стоимости ребер р ' ( u,ν ) необходимо найти множество оптимальных по Парето решений задачи ^miⁿ⁽ Q i ⁽ E У ^mi^{n( Q} 2 ⁽ E У

EE

Проанализировав расчетную сложность представленной задачи, можно сделать вывод, что она NP-трудна. Множество оптимальных по Парето решений экспоненциально зависит от размерности задачи (число компонентов в множестве Е ' ).

Для нахождения максимальной пропускной способности сети использовался модифицированный алгоритм «проталкивания предпотока» – «поднять в начало» [4]. Он представляет собой наиболее оперативный метод решения задачи о максимальном потоке (сложность 0| V |³) и является простым в реализации.

Нахождение множества Парето задачи оптимизации сети передачи данных методом ветвей и границ

Фиксированными для рассматриваемого подмножества решений являются ребра из Е ' , для которых определено, будут они достроены или нет. S-множеством с фиксированными ребрами рассматриваемого подмножества решений обозначим те, которые предположительно достроятся. Все вершины дерева ветвления отвечают подмножеству D области допустимых решений и включают в себя нижнюю L_p и верхнюю H_p оценки значения пары ( Q ₁( E *), Q ₂( E *)) на рассматриваемом подмножестве.

• 6 т елекоммуникационные системы

Нулевой уровень дерева, являющийся корневой вершиной, отвечает всей области допустимых решений D, а каждая вершина уровню k > 0 – подмножеству, которое возникает в ходе фиксирования первых k ребер (из множества Е ' ) сети. Из всех вершин (кроме листьев дерева ветвления, где отмечаются ребра из Е ' ) осуществляется ветвление на два подмножества, то есть происходит дихотомическое деление.

Первое из них возникает посредством фиксирования очередного ребра, исключая его добавление в S, то есть рассматриваемое ребро не предполагает построение в сети. Второе возникает посредством фиксирования очередного ребра с добавлением его в S, то есть оно предусматривает достраивание.

Функция ветвления является рекурсивной, на ее вход подается номер ребра k для исследования (при вызове функции с характеристикой k ребра с номерами от 1 до k – 1 фиксированы). Алгоритм запускается посредством вызова функции ветвления с аргументом 1.

Каждая вершина дерева ветвления предполагает вычисление верхней H_p и нижней L_p оценки решения р . Решению r ∈ R отвечает оценка ( Q ₁( r ), Q ₂( r )), если:

• 1)    L_p ≻ ( Q ₁( r ), Q ₂( r )), тогда решение r ∈ R ликвидируется из множества рекордов, так как имеется доминирующее решение;

• 2)    ( Q ₁( r ), Q ₂( r )) ≻ H_p, в этом случае ветвление из имеющейся вершины оканчивается, и рассматриваются иные подмножества решений;

• 3)    r Е R ∶ ( Q ₁( r ), Q ₂( r )) ≻ H_p , а рассматриваемая вершина дерева ветвления является листом, в этом случае решение р добавляется в множество рекордов R ( R = R U { p }) R. Иначе продолжается ветвление из текущей вершины посредством вызова функции ветвления с аргументом k + 1.

Таким образом, алгоритм множества R включает в себя все решения, оптимальные по Парето. Специфика заключается в том, что у предложенного алгоритма решения задачи оптимизации сети передачи данных при его реализации в множество рекордов добавляются решения с зафиксированными ребрами.

По итогам расчетных экспериментов можно сделать выводы, что при добавлении промежуточной оценки множество рекордов сильно разрастается. Подобная ситуация приводит к значительному увеличению времени работы алгоритма.

Оценка вычислительной сложности алгоритма

При худших обстоятельствах время работы метода ветвей и границ сопоставим с алгоритмом полного перебора. Метод ветвей и границ при подобном варианте работы не в состоянии отсечь ни одного подмножества решений и выстроить дерево ветвлений, куда входят уровни |Е ' |.

При этом уровень глубины i предполагает 2 ' вершины. В результате вычислительная сложность алгоритма аналогична методу полного перебора и составляет порядка Е ' 0(2^{|Е ' |}) • | V |³) .

Хотя расчетная сложность одинакова, среднее время работы метода ветвей и границ существенно меньше в отличие от алгоритма полного перебора. Требования по памяти рассматриваемого алгоритма обладают экспоненциальной зависимостью от размера входных данных, так как следует хранить все недоминируемые решения, которые удалось выявить при работе.

Модель и алгоритмы оптимизации сети передачи данных    7

В противном случае в памяти будет храниться 2^{|Е ' |} решений. В результате можно говорить о том, что требования по памяти составляют 0(2^{|Е ' |}) • |Е ' |).

Результаты вычислительных экспериментов

Итоги тестирования программной реализации метода ветвей и границ осуществлялись на языке C++. Расчетные эксперименты включали в себя поиск всего множества оптимальных по Парето решений для 100 разных сетей передач данных, которые были случайным образом сгенерированы, число ребер в множестве Е ' которых составило 15, 20, 25, 30, 35 и 40.

В таблице отражены статистические значения показателя t , отражающего минимальное и максимальное время работы в секундах в тестовом наборе задач.

Время работы метода ветвей и границ

|Е ' |	| V |	| Е |	t , с
15	[7;11;9]	[18;45;35]	[0.008;0.205;0.057]
20	[8;11;9]	[24;45;35]	[0.032;3.693;0.493]
25	[9;12;10]	[30;53;40]	[0.062;54.595;5.01]
30	[9;14;12]	[30;72;52]	[0.312;897.448;62.843]
35	[10;14;13]	[37;72;63]	[0.27;3541.633;297.496]
40	[11;16;13]	[45;93;72]	[11.886;65203.957;2689.295]

Заключение

В рамках исследования была построена математическая модель сети передачи данных в виде взвешенного ориентированного ациклического графа. Она принимает во внимание особенности современных сетей.

Кроме того, осуществлен анализ вычислительной сложности представленной модели. Проведена адаптация метода ветвей и границ, чтобы осуществлять поиск множества па-рето-оптимальных решений задачи оптимизации сети передачи данных. Также выполнена оценка трудоемкости и представлены итоги расчетных экспериментов.