Модель и анализ контактного взаимодействия с биотканями одномерных полимерных имплантатов
Автор: Шилько С.В., Черноус Д.А., Панин С.В.
Журнал: Российский журнал биомеханики @journal-biomech
Статья в выпуске: 1 (51) т.15, 2011 года.
Бесплатный доступ
Рассматривается базовый этап процесса имплантации в виде протягивания одномерного протезирующего (фиксирующего, диагностирующего) элемента через отверстие в биоткани. Разработанная механико-математическая модель описывает взаимодействие данного имплантата с биотканями в условиях сцепления и проскальзывания контактирующих поверхностей. Получены расчетные зависимости для удлинения имплантата и максимального значения интенсивности тензора напряжений в прилегающих объемах материала, позволяющие получить теоретическую оценку фрикционно-механических характеристик одномерных имплантатов и определить их травмирующее воздействие.
Биоткань, фрикционно-механические свойства, полимер
Короткий адрес: https://sciup.org/146216016
IDR: 146216016 | УДК: 531/534:
Текст научной статьи Модель и анализ контактного взаимодействия с биотканями одномерных полимерных имплантатов
В медицине широко используются методы и средства для протезирования, фиксации и диагностики органов, а также инъекций, основанные на введении в организм тонких и гибких сплошных или полых элементов (катетеров, игл, зондов, микрокабелей, шовного материала в виде нитей или проволоки и т.п.). С учетом весьма малого отношения радиуса поперечного сечения и длины указанные элементы можно рассматривать как одномерные имплантаты, обозначая в дальнейшем этим термином достаточно большую группу медицинских изделий. Помимо обеспечения ряда деформационно-прочностных показателей имплантатов, включая прочность, эластичность и формостабильность, необходимо минимизировать вызываемую их использованием травму и сроки заживления раны в целях быстрой и полной послеоперационной реабилитации пациентов. В результате иногда приходится выполнять противоречивые требования к физико-механическим свойствам материалов для изготовления указанных изделий. Поскольку практически все способы имплантации связаны с интенсивным контактным взаимодействием с биотканями, актуален также учет трения, оказывающего существенное влияние на манипуляционные показатели и травматичность изучаемых одномерных имплантатов.
Можно заметить, что имплантация (например введение зонда или формирование хирургического шва) представляет собой однократный либо повторяющийся акт перфорации биоткани и протягивания имплантата через образовавшееся отверстие. Теоретический анализ данного взаимодействия позволяет исходя из достаточно просто
Шилько Сергей Владимирович, к.т.н., завлабораторией механики адаптивных материалов и биомеханики ИММС НАН Беларуси, Гомель
Панин Сергей Викторович, д.т.н., завлабораторией ИФПМ СО РАН, Томск определяемых фрикционно-механических и геометрических параметров одномерного имплантата прогнозировать его манипуляционные свойства и травматичность. Целью настоящего исследования является построение механико-математической модели протягивания одномерного имплантата через фрагмент биоткани в виде мембраны.
Формулировка задачи и построение модели
В ходе обзора литературных источников [1–3, 5–7, 9, 11, 12] авторами не обнаружены публикации, содержащие подробное теоретическое описание процесса протягивания одномерного имплантата через перфорированную биоткань. Вместе с тем в механике композитов известны работы, в которых анализируется сходный процесс вытягивания волокна из объема материала матрицы, в частности, при экспериментальном определении сдвиговой прочности адгезионной связи «волокно – матрица» посредством « pull–out »-теста [13, 14]. Однако имеются существенные различия контактного взаимодействия одномерного имплантата с биотканями и армирующего волокна с матричным материалом в композитах:
-
1) из-за отсутствия сильной адгезии имплантата к биоткани предельное сдвиговое напряжение определяется законом Кулона, т.е. произведением контактного давления и коэффициента трения;
-
2) практикуемое изготовление имплантатов из низкомодульных полимеров и эластомеров делает необходимым учет изменения поперечного сечения имплантата в зоне контакта при натяжении;
-
3) толщина фрагмента биоткани, через который осуществляется протягивание, мала в сравнении с другими размерами фрагмента. В этом случае сила сопротивления при протягивании в основном определяется не упругими свойствами биоткани, а ее предварительным натяжением, как это имеет место в мембранах конечной толщины.
Отмеченные особенности не позволяют использовать известные методики, разработанные для оценки адгезионной прочности соединения жесткого волокна с эластичной матрицей в армированных композитах.
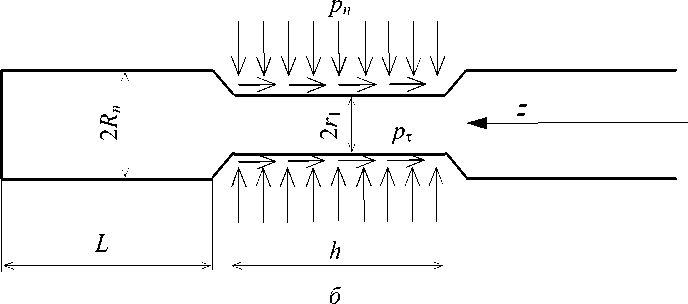
Схемы, представленные на рис. 1, иллюстрируют взаимодействие имплантата I и биоткани II. Принимается, что исходный радиус отверстия r 0 меньше радиуса нити R n . Элемент биоткани, через который осуществляется «протягивание», представляет собой мембрану толщиной h . Размеры мембраны в плоскости, перпендикулярной нити, существенно больше толщины h и радиуса R n .
Для описания напряженно-деформированного состояния мембраны введем цилиндрические координаты r , ϕ , z . Ось z перпендикулярна плоскости мембраны и проходит через центр отверстия. Координату z будем отсчитывать от свободного поперечного сечения нити. Элемент ткани находится в плоском напряженном состоянии: σ zz = σ rz = σ z ϕ = 0. Начальное натяжение биоткани будем характеризовать заданной компонентой тензора напряжений σ rr = σ 0 . При протягивании имплантата радиус отверстия становится равным r 1 .
С целью упрощения дальнейших выкладок введем допущение о независимости конечного радиуса отверстия r 1 от координаты z . Изменение радиуса отверстия по толщине мембраны обусловлено неоднородностью распределения осевого напряжения σ zz на участке имплантата, контактирующего с биотканью. Допущение о постоянстве радиуса r 1 не является принципиальным, но позволяет существенно упростить преобразования и получить аналитическое решение задачи. Увеличение размеров отверстия при протягивании вызывает дополнительные напряжения и деформации, для определения которых следует решить задачу теории упругости в осесимметричной постановке для плоского напряженного состояния. Также следует обеспечить отсутствие дополнительных напряжений на большом удалении от отверстия
F 0
Рис. 1. Расчетные схемы взаимодействия фрагмента биоткани (мембраны) и имплантата в поперечном (
а
) и продольном сечении (
б
). Пунктирной линией
1
показано исходное отверстие в биоткани; пунктирной линией
2
показано сечение имплантата в недеформированном состоянии;
p
n
,
p
τ
– нормальное и касательное контактные напряжения;
h
– толщина мембраны;
L
– длина имплантата между точкой приложения силы и мембраной
(при r → ∞). Решение поставленной задачи в перемещениях имеет вид [4] (r - r )r ur = 1 0 0 , uz = u = 0. На имплантат со стороны биоткани будет действовать rϕ нормальное давление pn, значение которого определяется по формуле p = Et(r1 -r0)-σ .
n r
0 (1
+
ν
t
) 0
Представим имплантат в виде круглого стержня из упругого материала с модулем Юнга
E
n
и коэффициентом Пуассона
ν
n
. Для расчетной оценки конечного радиуса
r
1
необходимо учесть уменьшение радиуса относительно исходного значения
R
n
. Пренебрежение зависимостью радиуса
r
1
от координаты
z
позволяет рассматривать поперечное сжатие независимо от процесса протягивания, т.е. предполагается, что осевое напряжение
σ
zz
равно нулю. Соответствующее решение имеет вид [8]
R
-
r
2
ν
(
R
-
r
)
u
= -
n
1
r
,
u
=
n n
1
z
,
u
=
0. Приравняв на границе контакта
r R
n
z R
n
(1
-ν
n
)
ϕ
радиальные напряжения в стержне и биоткани, для определения радиуса r1 получим уравнение, решение которого имеет вид r =----
1 1
+
Z
ZR
n
+
r
1 + к °0(1 + V t))
E
t
Л . Здесь для краткости записи введено обозначение
Z
=
Е
п
Г
о
(1
+ v
t
)
E
t
R
n
(1
-v
n
)
.
Тангенциальное контактное напряжение
p
T
при наличии сцепления прямо пропорционально упругому смещению
u
z
точек поверхности
p
T
=
kuz
.
Для определения коэффициента
k
рассмотрим прогиб мембраны элементарной толщины
dz
с отверстием радиуса
r
1
. В мембране действует радиальное напряжение
с
0. Периметр отверстия смещается на величину
u
z
. Поскольку радиус мембраны много больше смещения
u
z
, можно пренебречь изменением радиального напряжения при прогибе. Тогда сила сопротивления, действующая со стороны мембраны, будет определяться по формуле
Tz
=
2
лс
0
u
z
dz
. Представляя эту силу как результирующую равномерно распределенного по внутренней поверхности отверстия тангенциального напряжения, получим выражение для коэффициента пропорциональности в (3)
k = ^0-r1 . Далее рассмотрим равновесие участка имплантата в области контакта с биотканью. Этот участок представляет собой цилиндр длиной h и радиусом r1. На одной из торцевых поверхностей цилиндра действует продольная сила F0. Противоположная торцевая поверхность свободна от нагрузок. Уравнение равновесия элементарного участка цилиндра длины dz можно записать в виде dF
— =
2
n
rp
t
.
dz
Здесь
F
z
– продольная сила, для которой выполняются граничные условия
F
z
(0) = 0,
F
z
(
h
) =
F
0
. Сила
F
z
связана с продольной деформацией стержня следующим образом:
F
z
du
=
Zn
П
r
1
^
zz
=
Zn
П
r
1 -Г .
dz
Здесь
Z
n
=
E
n
(1
-V
n
)
(1
+ v
n
)(1
-
2
v
n
)
. Подставив выражения для продольной силы и напряжения pT в выражение (5), получим d u 2k 2
—z-
=---
uz
=
D U
.
dz
2
Z
n
r
1
z z
Здесь для краткости дальнейших выкладок введен коэффициент D =
2
k
1
Z
n
r
1
.^0-. Равенство (7) представляет собой дифференциальное уравнение
r
1
Z
n
, -
Dz
.
для функции
u
z
(
z
). Общее решение этого уравнения имеет вид
uz
=
C
1
eDz
+
C
2
e
Значения констант C1 и С2 определяются из граничных условий для продольной силы с учетом равенства (6). После преобразований получим uz
F
o
(
e
Dz
+
e - Dz
)
DZ
„
п
r
.
(
eD
h
-
e
-
Dh
)'
Функция (8) при увеличении координаты
z
возрастает. Следовательно, тангенциальное напряжение при
z
=
h
достигает максимума, значение которого вычисляется по формуле
p max T F = kuz (h) = —0- п гЛ2 Z.
°
0
e
Dh
+
e
-
Dh
n
e
Dh
- e
-
Dh
Сцепление с биотканью сохраняется до тех пор, пока напряжение
p
T
не достигнет предельного значения, определяемого по закону Кулона
p
k
=
f pn
. Здесь
f
сц
– коэффициент трения покоя для данной пары «нить – ткань». Используя соотношение (9), можно определить значение продольной силы
F
0
kr
, при которой начнется проскальзывание нити:
_ Dh
-
Dh \
2
Z
„
(
e
-
e
)
F
=
f
сц
Pn
п
r
2
V _ / Dh . -Dh V
\ °
o
(
e
+
e
)
Если продольная сила превышает значение F0, область контакта нити с биотканью разделяется на два участка длиной l1 и l2 соответственно (l1 + l2 = h). На участке от z = 0 до z = h выполняется условие сцепления (3), и для смещения выполняется уравнение (7). Граничное условие на свободной поверхности имеет вид Fz(0) = 0. На границе раздела участков (при z = l1) напряжение pT принимает значение pkr. Следовательно, u(1)(lx) = :цР" . С учетом данных граничных условий решение 1 z k уравнения (7) примет вид uz(1)
f
сц
P
n
(
e
Dz
+
e"Dz
)
k
(
e
D
+
e
Dl
)
На втором участке длиной 12 выполняется равенство pT = f,кpn и реализуется проскальзывание. Здесь fск – коэффициент трения. Для упругого смещения справедливо уравнение d2U^ = 2nrLf „ =н
7 2 Г7 2
f
ск
p
n
H
.
dz Zn
п
r*
i
2
f p
Здесь введен коэффициент
H
= —с^-
"-
. На решение уравнения (12)
Z
n
r
1
накладывается граничное условие
F
z
(
h
) =
F
0
при
z
=
h
. Также следует обеспечить неразрывность смещений
u
Z
1^(
1
1
)
=
u
Z
2)
(
1
2) при
z
=
1
1
. С учетом указанных граничных условий решение уравнения (12) имеет вид
U
(2) _
f
сц
p
"
zk
+
_FL_
I
Z"
п
Г
1
2
- Hh (z -11) +H (--2 -1.2). Условие неразрывности первой производной от упругого смещения при переходе от одного участка к другому приводит к уравнению Dfсц Pn ( eDl - e"Dl1 ) k (eD + eD )
F
0
Z
n
П
ri
- H (h - lx).
В результате решения данного нелинейного уравнения при заданной силе
F
0
определяется длина участка сцепления
l
1
. В момент начала проскальзывания
l
1
=
h
значение силы
F
0 совпадает с
F
0
kr
. При распространении проскальзывания на всю толщину мембраны длина участка сцепления
l
1
= 0. Значение приложенной силы
F
0ск , при которой
l
1
= 0, определяется из уравнения (14) следующим образом
F
T
=
Z
n
п
r
2
Hh
=
2
п
r hf
ск
P
n
.
Таким образом, при действии продольной силы
Fo
<
F
0
k
удлинение имплантата согласно соотношению (8) определяется по формуле
и =
F
0
L
+
F
o
(
e
Dh
+
e"
Dh
)
En пRn2 + Zn пr D (eDh - e"Dh)"
Здесь
L
– длина имплантата между точкой приложения силы и мембраной. Для значений силы в диапазоне [
F
0
kr
,
F
0
ск
] удлинение имплантата вычисляется по формуле
и = FL + F^ + f^ - H (h -1 )2. E„ nRn2 Z„ nr2 k 2V 17
n n n
1
Длина
l
1
в выражении (17) определяется из решения уравнения (14).
Соотношения (16) и (17) позволяют установить расчетную зависимость удлинения нити от продольной силы
F
0
. Кроме того, разработанная методика может быть использована для оценки максимального значения интенсивности тензора напряжений
о
max
, которое характеризует предельное состояние и вычисляется по известным зависимостям [8, 10]:
•
для биоткани
•
для имплантата
о
о
U
m
,"
=
V
P
n
+
3
(
P
.-
)
;;
max
un
+
P
n
+
P
n
°
zz
+
3
(
P
max
)
2
.
В этих выражениях давление
p
n
определяется согласно (1) с учетом (2). В диапазоне значений продольной силы
F
0
<
F
0k
величина
p
max
вычисляется по формуле
F
(9) и
о
zz
= —0-
. Интенсивность тензора напряжений принимает максимальное значение
п
r
,
2
в области контакта (
r
=
r
1
) вблизи поверхности биоткани
z
=
h
. Если значение продольной силы лежит в диапазоне от
F
0
kr
до
F
0ск , в формулах (18) и (19) следует принять
P
/ =
f „P
n
.
о== -°т -
Z
.
H
(
h
-
1
1
)
. (20)
п r, Максимальная интенсивность напряжений достигается на границе раздела участков сцепления и проскальзывания. Пример использования математической модели
Разработанная механико-математическая модель протягивания одномерного имплантата позволяет установить зависимость его удлинения от приложенной продольной силы и получить расчетную оценку максимальной интенсивности напряжений в имплантате и биоткани. Исходными параметрами являются упругие характеристики биоткани (
E
t
,
v
t
) и имплантата (
E
n
,
v
n
), исходные значения радиусов отверстия (
r
0
) и имплантата (
R
n
), толщина (
h
) и начальное натяжение (
о
0) биоткани, коэффициенты трения покоя (
f
сц
) и скольжения (
f
ск
) для пары «имплантат – биоткань». Предварительно по формуле (2) определяется радиус отверстия после деформации
r
1
. Затем по формуле (1) вычисляется давление биоткани на имплантат
p
n
. Согласно равенствам (4), (7) и (12) вычисляются введенные коэффициенты
k
,
D
и
H
соответственно. После этого с использованием соотношений (10) и (15) определяются значения силы
F
0
kr
и
F
0ск . В результате решения уравнения (14) для заданного значения силы
F
0
вычисляется длина участка сцепления
l
1
. При подставлении полученных значений в формулы (16)–(19) при заданной продольной силе определяются удлинение имплантата
и
и максимальные значения тензора напряжений в имплантате
о
max
и биоткани
о
max
.
В качестве примера использования разработанной методики рассмотрим процесс протягивания полиэфирной нити с параметрами
E
n
= 25 МПа;
v
n
= 0,4;
R
n
= 0,2 мм через отверстие в биологической мембране, свойства которой соответствуют упругим характеристикам кожи человека в области живота
E
t
= 1,1 МПа;
v
t
= 0,48, приведенным в работе [3]. Значения остальных исходных параметров были приняты следующими:
r
0 = 0,13 мм;
h
= 6 мм;
о
0 = 0,1 МПа;
f
;ц = 0,6;
f
;к = 0,5;
L
= 0.
Согласно полученным расчетным данным (рис. 2) до начала проскальзывания (
F0
<
F
0k
) зависимость удлинения нити от приложенной силы практически линейна. Для сил
F
0
>
F
k
условная жесткость нити, равная производной от силы по удлинению, по мере удлинения плавно уменьшается.
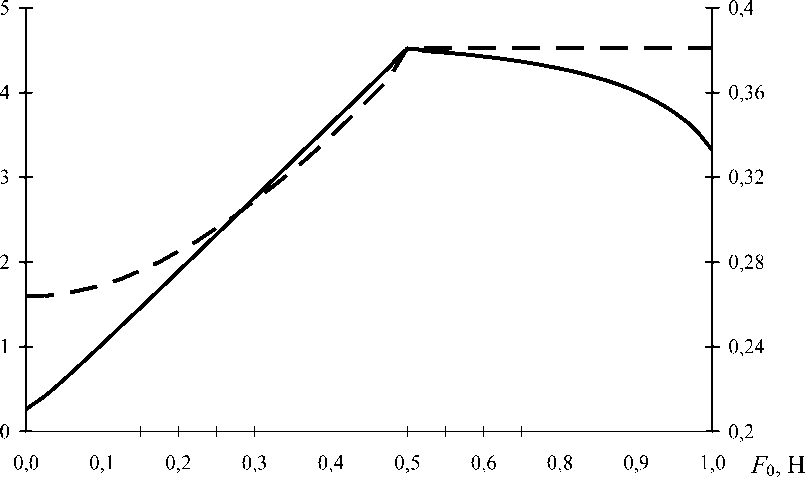
Из зависимостей, приведенных на рис. 3, следует, что для использованных исходных данных интенсивность напряжений в нити существенно (на порядок) превышает интенсивность напряжений в коже. До начала проскальзывания интенсивность напряжений в имплантате растет практически линейно с увеличением приложенной силы. На этой стадии максимальная интенсивность напряжений в биоткани при увеличении силы
F
0
возрастает нелинейно. После начала проскальзывания максимальная интенсивность напряжений в нити плавно снижается, а в коже остается неизменной.
Рис. 2. Зависимость «сила – удлинение»
σ
u
m
n
ax
, МПа
σ
u
m
t
ax
, МПа
Рис. 3. Зависимость максимальной интенсивности тензора напряжений в нити (сплошная кривая) и коже (пунктирная) от приложенной силы Заключение Разработана механико-математическая модель, описывающая процесс протягивания одномерного эластичного имплантата через фрагмент биоткани в виде мембраны с отверстием. Установлено, что при превышении определенного порогового значения усилия протягивания наблюдается снижение жесткости исследуемой системы с ростом удлинения имплантата, причем характер зависимости максимальных значений интенсивности напряжений от приложенной силы различен для имплантата и биоткани. Разработанная методика и установленные закономерности могут быть использованы для прогнозирования манипуляционных характеристик и травматичности одномерных имплантатов на основании данных о фрикционно-механических свойствах используемых материалов. Благодарности Работа выполнена при поддержке БРФФИ-РФФИ: проекты Ф10-240 (10-08-90011-Бел_а), Т10СО-033, а также 09-08-00752-а.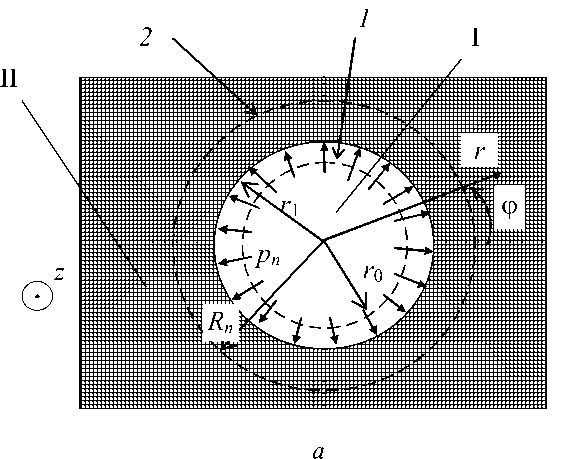
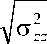
Список литературы Модель и анализ контактного взаимодействия с биотканями одномерных полимерных имплантатов
- Бурсина Н.В., Винокурова Т.И., Гаврилюк Н.Н. Критерии, методы оценки свойств и технология получения шовных материалов. -Киев: Изд-во ИПМ, 1987.
- Буянов В.М., Егиев В.Н., Удотов О.А. Хирургический шов. -М.: Рапид-Принт, 1993. -103 с.
- Винокурова Т.И., Кирюхин С.М., Фёдорова Е.Ф. Выбор метода оценки жесткости хирургических нитей//Известия вузов. Технология текстильной промышленности. -1997. -Т. 236, № 2. -С. 6-9.
- Кристенсен Р. Введение в механику композитов. -М.: Мир, 1982 -334 с.
- Пучков К.В., Селиверстов Д.В., Гаусман Б.Я., Швальб А.П. Сравнительная оценка реакции тканей на синтетические шовные материалы, применяемые в абдоминальной хирургии//Вестник Рос. ассоц. акушеров-гинекологов. -1996. -№ 1. -С. 30-34.
- Сандаков П.Я., Егиев В.Н., Тепликов А.В., Шадрин В.В. Оценка «пилящего» эффекта шовных материалов, используемых в абдоминальной хирургии//Современные подходы к разработке эффективных перевязочных средств, шовных материалов и полимерных имплантатов: материалы 3 междун. конф. -М., 1998. -С. 164-165.
- Семенов Г.М., Петришин В.Л., Ковшова М.В. Хирургический шов. -СПб: Питер, 2002. -256 с.
- Старовойтов Э.И. Основы теории упругости, пластичности и вязкоупругости. -Гомель: БелГУТ, 2001. -344 с.
- Шадрин В.В., Тепликов А.В. Манипуляционные характеристики хирургических нитей//Российский журнал биомеханики. -2001. -Т. 5, № 3. -С. 41-50.
- Шилько С.В., Черноус Д.А., Анфиногенов С.Б., Курек М.Ф. Механические и фрикционные свойства биоэластомеров. Ч. 1: Описание релаксационных зависимостей кожи человека при растяжении//Российский журнал биомеханики. -2008. -Т. 12, № 3. -С. 44-51.
- Cavaliere R. Suture materials. Properties and uses//J. Amer. Pediatry Assoc. -1983. -Vol. 4. -P. 57-64.
- Chu C.C. Mechanical properties of suture materials: an important characterization//J. Annals of Surgery. -1983. -Vol. 193, No. 3. -P. 365-370.
- Dutch V., Pisanova E., Zandarov S., Lauke B. "Fundamental" and "practical" adhesion in polymer/fiber systems//Mechanics of Composite Materials. -1998. -Vol. 34, № 4. -P. 431-446.
- Nayfeh A.H. Thermomechanically induced interfacial stresses in fibrous composites//Fibre Sci. Techn. -1997. -No 10. -P. 195-209.


