Модель идеального фазового детектора

В настоящее время широкое распространение в области связи [1–3], радионавигации [4–5] и радиолокации [6] получили радиотехнические системы (РТС), которые в качестве носителя информации используют фазу радиосигнала, что связано с ее большими информативными способностями по сравнению с огибающей. В большинстве из перечисленных РТС применяемые радиосигналы являются импульсными. Следует учитывать, что фаза радиоимпульсного сигнала является легкоуязвимым параметром и степень его искажения зависит от построения фазового канала РТС, содержащего полосовые фильтры, которые часто реализованы на сосредоточенных элементах, что обусловлено тенденцией к миниатюризации радиоэлектронных систем [7].

При работе РТС по стационарному сигналу систематическая ошибка по фазе минимизируется путем соответствующей калибровки. Однако тенденция к ускорению передачи и обработки информации в РТС приводит к необходимости работы в динамическом режиме, когда съем информации о фазе осуществляется уже при переходных процессах, протекающих в элементах тракта РТС, которые могут существенно исказить фазу радиосигнала, что может стать причиной недопустимых ошибок [7]. Таким образом, получение точной информации об искажениях фазы радиоимпульсного сигнала (обеспечения операции «идеального» детектирования), вызванных переходными процессами в элементах тракта фазового канала РТС его прохождением, наиболее актуально.

Такая информация может быть получена двумя подходами: 1) с использование аналитического анализа переходных процессов или 2) с помощью методов численного моделирования. Первый из них удобен, когда канал представляет собой каскадное соединение однотипных избирательных звеньев, а второй используется при более сложном его построении.

• 1.    Постановка задачи

Для вычисления фазы радиосигнала в программных средах численного моделирования применяются следующие методы: 1) метод определения медленно меняющейся фазы у аналитического сигнала; 2) квадратурный приемник; 3) метод определения фазы у комплексной огибающей (метод медленно меняющихся амплитуд) высокочастотного заполнения, когда при моделировании полосовые избирательные системы заменяются на низкочастотные системы-прототипы, обеспечивающие фильтрацию высоких частот.

У перечисленных выше методов, несмотря на их широкое распространение, имеется ряд недостатков, которые существенно влияют на определение фазы радиосигнала.

Метод, основанный на использовании аналитического сигнала, имеет следующие недостатки: 1) отсутствие учета изменения медленно меняющейся фазы по четвертям комплексной плоскости [8]; 2) существует дефект, связанный

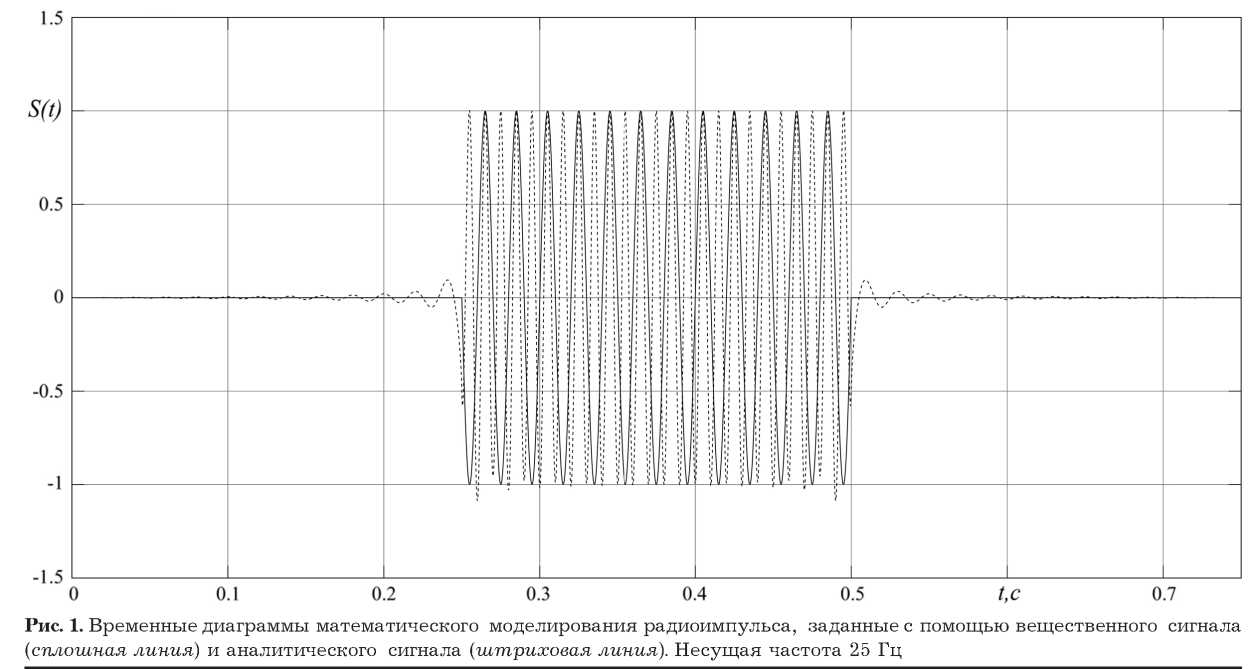
Рис. 2. Структурная схема квадратурного приемника: 1 – смеситель; 2 – генератор несущей; 3 – фазовращатель на п /2; 4 — ФВЧ; 5 — вычислитель фазы

с отсечением части спектра, переходящего из области положительных в область отрицательных частот и с последующим ее замещением на комплексно-сопряженную с ней часть составляющего спектра сигнала, переходящего из области отрицательных частот в область положительных частот, что является необходимым и и похожий на явление Гиббса в теории спектров, но при этом описываемый более сложной функциональной зависимостью. В частности, данный дефект приводит к наличию предвестника и следа [8–10].

Вышеуказанный дефект можно наблюдать в широко используемой программе математического моделирования Matlab – Simulink (рис. 1).

Недостатком второго метода является появление нелинейных искажений, вызванных преобразованием частоты, с последующим наложением на них линейных искажений от фильтрующих систем, что в итоге будет влиять на точность определения фазы. Это легко можно увидеть, анализируя алгоритм его работы (рис. 2).

Исходный сигнал в форме квазигармоническо-го колебания, действующий на входе квадра- турного приемника, имеет вид

где too - несущая частота (средняя частота спектра) сигнала; H (t) - модуль физической огибающей; ф(t) - медленно меняющаяся фаза; фо -начальная фаза; As (t) - синфазная и Bs (t) -квадратурная составляющие, определяющие поведение модуля физической огибающей и медленно меняющейся фазы квазигармонического колебания и связанные с ними следующими со- отношениями:

H (t ) = V As 2 (t) + Bs 2 (t); ф( t ) = arg ( As ( t ) + jBs ( t )) .

Сигналы I (t) синфазной и Q (t) квадратурной составляющих, получаемые на выходе смесителей (блоки 1, рис. 2), определяются следующи- ми соотношениями:

• -    B s ( t ) sin ( to o t + Ф о ) ) cos ( to o t + Ф о ) =

• -    B s ( t ) sin ( 2 ® 0 t + 2 ф о ) ] ;

• -    B s ( t ) sin ( to o t + Ф о ) ) sin ( to o t + Ф о ) =

= 2 [ ^As ⁽ t ) ^{sin ( 2 to} 0 t ^{+ 2 ф} 0 ) ^-

• -    B s ( t ) + B s ( t ) cos ( 2 to o t + 2 ф о ) J .

  
  

После фильтрации данных сигналов ФВЧ (блоки 4, рис. 2) на их выходах мы получаем сигналы оценок As(t) синфазной и Bs(t) квадратурной составляющих исходного радиосигнала, которые определяются как

t

t

Bs(t) = Q (0) h (t) + J Q' (T)h (t - t) dt,

где h ( t ) — переходная характеристика ФВЧ.

Далее сигналы A s ( t ) и B s ( t ) поступают на вычислитель фазы, производящий вычисление оценки фазы (блок 5, рис. 2)

^Sвых ( t ) = Ф ( t ) = arg ( ^As ( t ) ^{+ jB}s ( t ) ) . ⁽⁶⁾

К недостаткам третьего из данных методов можно отнести тот факт, что оценка фазы производится с помощью использования комплексной огибающей в силу применения метода медленно меняющихся амплитуд, при этом рассматриваемые фильтры должны обладать симметричными АЧХ и ФЧХ, а величина расстройки, при ее наличии, должна быть малой [11]. Таким образом, данный метод не применим для сложных избирательных систем, имеющих несимметричные частотные характеристики, которыми, в частности, обладают широкополосные избира- тельные полосовые системы.

При этом следует отметить, что для данного метода в работе [12] была указана возможность учета несимметричности АЧХ и ФЧХ у избирательных полосовых систем при их аналитическом анализе, однако, насколько известно авторам, в программах моделирования для данного случая она не была реализована.

Таким образом, на основании проведенного выше анализа возникает потребность в решении задачаи, заключающейся в необходимости формирования нового подхода для вычисления фазы радиосигнала в программных средах, реализующих математическое моделирование, который бы обеспечивал: 1) учет влияния несимметричности АЧХ и ФЧХ линейных избирательных систем; 2) решение проблемы АФЧ [7]; 3) операцию «идеального» детектирования.

2. Решение задачи

При решении поставленной задачи исходим из того, что для линейных избирательных си- стем c постоянными параметрами выполняется принцип транспозиции (инвариантности гармонического воздействия и реакции): при гармоническом воздействии в цепи со временем устанавливается стационарный режим, в котором напряжение между ее узлами и токи, протека- ющие по ее ветвям, изменяются по гармоническому закону с частотой, равной частоте воздействия. В этом случае структурная схема, реализующая решение поставленной задачи, будет иметь вид, представленный на рис. 3.

Рассмотрим принцип работы при предлагаемом подходе. Исходный радиосигнал с заданной огибающей A ( t ) ( -» <  A ( t ) < +» ), у которого фаза подвергается манипуляции, формируется в комплексном виде (блок 1, рис. 3) и имеет вид

sвх (t) = A (t) exP (j (to0t + Ф (ktс ))) =

где { Ф ( k t с ) } — манипулирующая псевдослучайная последовательность фа з; l – число символов в последовательности; k = 1, l ; т с — длительность символа; to o — несущая частота.

Далее сигнал (7) поступает на вход блоков 2 и 3, которые выделяют его действительную и мнимую составляющие соответственно. Таким образом, на выходе блока 2 будем иметь вещественный сигнал, определяющий действительную составляющую комплексного сигнала (7)

S ex . Im ⁽ t ) = ^A ( t ) ^sin ( ^to 0 t + Ф ( ^{k т} с ) ) . ⁽⁹⁾

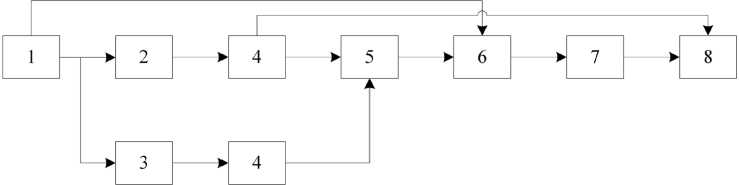
Рис. 3. Структурная схема предлагаемого подхода, реализующего принцип «идеального» фазового детектора: 1 – генератор комплексного сигнала радиосигнала с заданной огибающей и манипулированной фазой; 2 – блок выделения действительной части комплексного радиосигнала; 3 – блок выделения мнимой части комплексного радиосигнала; 4 – линейная полосовая избирательная система; 5 – блок преобразования двух вещественных сигналов для мнимой и действительной части в комплексный сигнал; 6 – смеситель; 7 – блок выделения модуля и аргумента комплексного числа; 8 – блок построения медленно меняющейся фазы радиосигнала на выходе избирательной системы в точках касания огибающей сигнала (10)

Затем каждый из вещественных сигналов (8) и (9) пропускается через две идентичные линейные полосовые избирательные системы (блоки 4, рис. 3), на выходе которых мы получаем преобразованные вещественные сигналы для действительной и мнимой составляющей соответствен- но, определяемые следующим образом:

^ ых .Re ( t ) = S ex .Re ( 0 ) h ( t ) ⁺

t

+ IX .Re' (T) h ( t -T) d T =

₀                                                   (10)

= | ^Авых ⁽ t )| cos ^(to 0 t ⁺ V вых ⁽ t ) ) ,

^ых .Im ⁽ t ) S ex .Im ^{( 0 )} h ⁽ t ) ⁺

t

+ J Sex .Im' (T)h (t -T) d T = вых          0     вч.вых

= A

вых

(t)| sin (tot + Vвых (t)) , где h (t) — переходная характеристика линейной избирательной системы; Авых (t) — огибающая радиосигнала, прошедшего через избирательнУю систему; Vвых (t) = ф вч. вых (t)+ Y ог. вых (t) медленно меняющаяся фаза радиосигнала, прошедшего через линейную избирательную систему; Фвч.вых (t) — составляющая медленно меняющейся фазы, обусловленная высокочастотным заполнением; уог.вых (t) — составляющая медленно меняющейся фазы, определяющая знак огибающей

Aвых (t )| exp [j (to0t + V вых (t))].

Далее сигнал (12) поступает на блок 6, выполняющий операцию преобразования частоты, таким образом, сигнал на его выходе будет определяться следующим образом:

A вых ( t )| exp ^[ j ( v вых ( t ) ) ] ,

Блок 7, на который поступает сигнал (13), выполняет операцию вычисления модуля и аргумента комплексного числа. Получаемая таким образом информация далее используется для определения значения медленно меняющейся фазы радиосигнала в точках касания огибающей вещественного сигнала (10). Указанную операцию выполняет блок 8.

Анализируя операции, выполняемые подходом, представленным на рис. 3, и выражения (7)–(13), можно утверждать, что он обеспечивает единственность взаимосвязи между действительной и мнимой частью формируемого комплексного сигнала и после его прохождения через избирательные системы, а следовательно, и при определении фазы, обеспечивая операцию «идеального» детектирования и не накладывая ограничения на симметричность АЧХ и ФЧХ рассматриваемой полосовой избирательной системы.

^Y ог . вых

(t) =

0,

п,

a (t) ^ 0;

Далее сигналы (10) и (11) поступают на блок 5, который преобразует два вещественных сигнала в один комплексный сигнал, т. е.

3. Аппробация подхода на примере среды моделирования Matlab – Simulink

Схема, реализующая представленный подход, за исключением блока 8, реализована в виде модели Simulink и представлена на рис. 4.

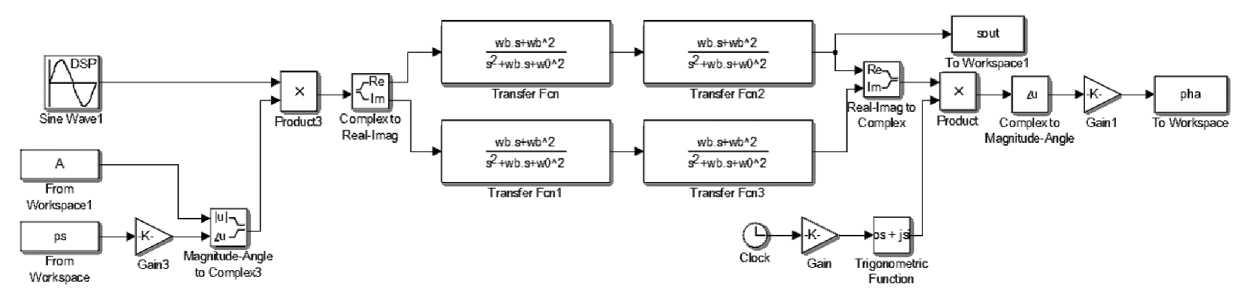
Рис. 4. Математическая модель, реализующая предлагаемый подход в среде Simulink

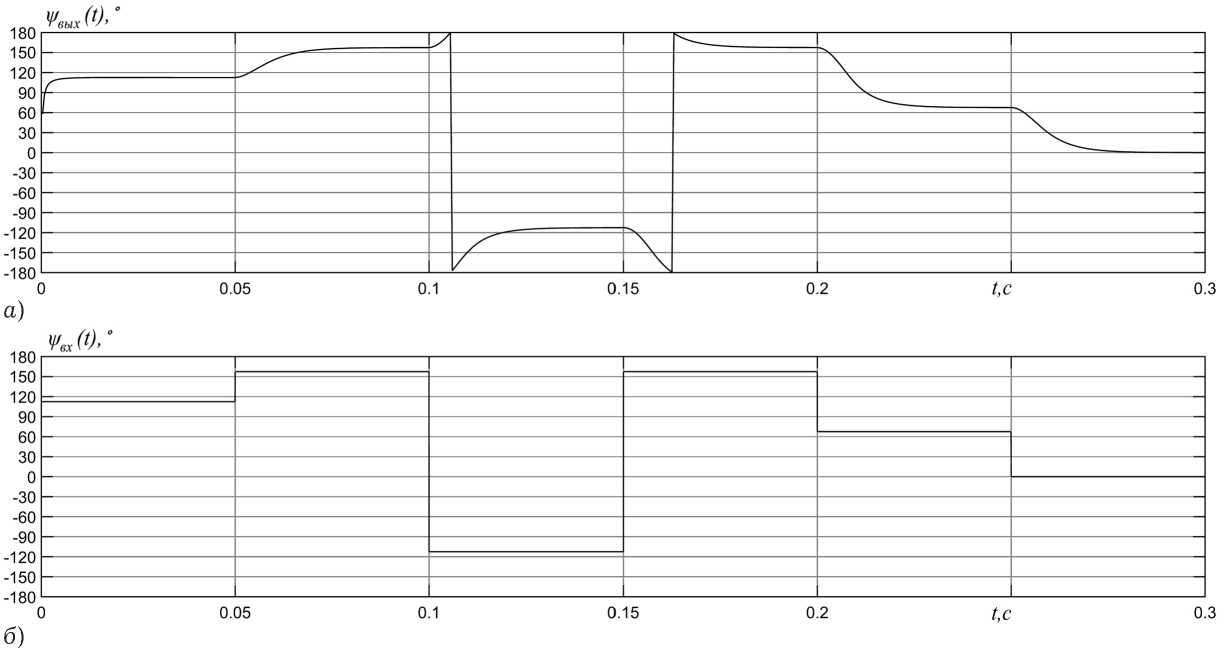
Рис. 5. Временные диаграммы зависимости медленно меняющейся фазы ФМн-16-сигнала на выходе ( а ) и входе ( б ) настроенного двухкаскадного резонансного фильтра. Резонансная частота 1 кГц, отношение резонансной частоты к результирующей полосе пропускания 25. Число символов в последовательности равно 6, длительность символа составляет 50 мс

Блок 8 реализован виде программного кода Matlab. В качестве линейной избирательной системы используется двухкаскадный резонансный фильтр.

Результаты моделирования прохождения ФМн-16-сигнала, состоящего из 6 символов, через настроенный двухкаскадный резонансный фильтр представлены на рис. 5.

Как видно из представленных результатов, данный подход отвечает поставленным требованиям решаемой задачи.

Заключение

В результате хотелось бы сделать следующий вывод: предложенный подход моделирования позволяет исследовать сложные фазовые каналы РТС, содержащие полосовые фильтры с учетом несимметричности их АЧХ и ФЧХ, обеспечивая «идеальное» детектирование.