Модель информативности данных на основе пакетов прикладных программ для нефтегазовой отрасли
Автор: Орлова И.О., Даценко Е.Н., Авакимян Н.Н., Гнеуш В.С.
Журнал: Международный журнал гуманитарных и естественных наук @intjournal
Рубрика: Технические науки
Статья в выпуске: 1-2 (76), 2023 года.
Бесплатный доступ
В статье рассматривается модель расчета информативности признаков и диагностических коэффициентов для отнесения нефтяной скважины к одному из множеств на примере пакетов математического моделирования MathCAD. В исследовании проведен метод расчета и статистический анализ данных. На основании данного анализа, выявлено, что данный расчет повысит эффективность и качество обработки информации в нефтегазовой отрасли.
Модель, информативность, диагностический коэффициент, распознавание, прогноз, множество, нефтедобыча, скважина, пакет прикладных программ
Короткий адрес: https://sciup.org/170197680
IDR: 170197680 | DOI: 10.24412/2500-1000-2023-1-2-94-99
Текст научной статьи Модель информативности данных на основе пакетов прикладных программ для нефтегазовой отрасли
Допустим, два множества объектов располагают общим для них признаком. Если значения данного признака различны для каждого множества объектов, то признак считается информативным, поскольку отделяет одно множество объектов от другого множества объектов. В противном случае, признак не обладает информативностью, поскольку не различает объекты, относящиеся к различным множествам [3].
Чем больше множеств, групп или образов различает признак, тем выше его информативность и наоборот. При этом дисперсионный анализ, а именно, критерий Фишера [4] и иные статистические критерии не в состоянии рассчитать величину информативности признака. Количественно оценить информативность признаков в состоянии осуществить мера Кульбака [5].
Рассмотрим такой расчет на конкретной задаче.
Задача . Даны коэффициенты нефтеотдачи для 115 объектов нефтедобычи, которые описываются следующими факторами (признаками):
-
1) количеством закачанной воды V3aH в объёмах нор;
-
2) темп разработки Т ;
-
3) проницаемостью пласта, к, мД ;
-
4) плотностью сетки скважин
S, га/скв;
-
5) содержание глины в коллекторах
Сг , % вес ;
-
6) содержание смол в нефти С , %вес ;
Объекты распределяются на два множества А и В : у первого множества коэффициенты нефтеотдачи п < 0,4, у второго множества п > 0,4. Различия в значениях признаков для пары множеств заключаются в следующем.
Для первого из признаков -количество прокачанной воды, - имеется диапазон значений [0;450]. Указанный диапазон разбивается на 9 интервалов (Таблица 1), количество интервалов может быть от 8 до 12 интервалов.
Расчёты в ячейках Таблицы 1 производятся с помощью пакетов прикладных программ MathCAD . (Рисунок 1).
В графы 3 и 4 помещаются данные по частоте попадания месторождений из множеств А и В в каждый из интервалов. Графы 5 и 6 содержат данные относительных частостей в процентах, при этом принимается за 100% сумма частостей применительно к А и В по всем диапазонам.
Таблица 1. Расчёт информативности для признака 1
y 2 = ( У 1 + 2 У 2 + 4 У 3 + 2 У 4 + У 5 )/10 (1)
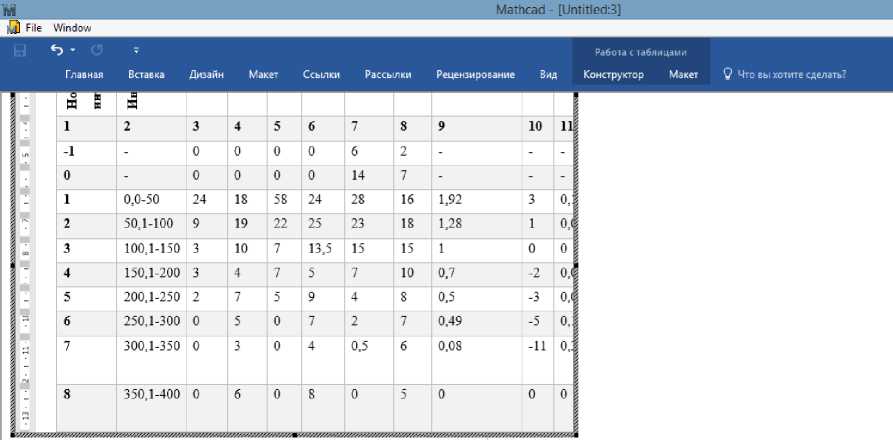
Рис. 1. Фрагмент ввода исходных данных в таблице для вычисления в Mathcad
Для первого интервала вводятся дополнительно несуществующие интервалы 0 и — 1, в которых в связи с отсутствием наблюдений, частости в диапазонах нулевые: у0 = уч = 0 .
Сглаженная частость для первого и второго интервала для группы А рассчитывается так:
у1А = (0 + 0 + 4 у + 2 у 2 + у )/10 = (0 + 0 + 4 • 58 + 2 • 22 + 7)/10 * 28
у2л = (0 + 2 у + 4 у 2 + 2 у 3 + у 4)/10 = (0 + 2 • 58 + 4 • 22 + 2 • 7 + 7)/10 * 23
Сглаженные значения частостей в % округляются до целых значений, при значениях меньше 5% округление производится до 1 знака после запятой. В столбце 9 приведено отношение сглаженных ча- стостей ул/ув. В столбце 10-диагностические коэффициенты (ДК), которые вычисляются следующим образом:
ДК = 10ig( y V y , )
Поскольку сглаженные значения частостей имеются в интервалах 0 и — 1, то средневзвешенные величины y , y и y суммируются, а полученная сумма счита-
^ = 48 = 1,92 ;
y B 1 25
Столбец 11 Таблицы 1 заполняются значениями информативности признака для всех диапазонов.
ется средневзвешенной частостью у признака для первого интервала:
ДК = 10lg1,92 = 3.
В соответствие с формулой Кульбака величина информативности J i — го интервала j — го признака рассчитывается следующим образом:
J ( x j ) = ДК ( x )1
i
i
хх
Р (- j -) — P ( - j -)
AB
где ДК ( x j ) -диагностический коэффициент I — го интервала j — го признака;
хi j
Р(—) -вероятность (сглаженная частость) A того, что в группе А I — го интервала отме чено попадание j — го признака, уд,;
хi
P () = Уш*
B
В составе диагностической таблицы определяется информативность признака во всех интервалах и находится совокупная информативность признака Xj :
J ( x j ) = £ J ( x j )
Информативность показателя «количество закачанной воды» для первого интервала
[ 0;50 ] равна:
J = 3 - -^(0,28 - 0,16) = 0,18, для второго интервала
-
J = 1 - ^(0,23 - 0,18) = 0,025. Информативность рассматриваемого признака вычисляется как сумма информативности в диапазонах JB = 0,72. Таким же образом вычислены информативности остальных указанных вначале признаков (Таблица 2, 3, 4).
Таблица 2. Расчёт информативности для признака 2
|
OS а § § а * и S |
я аа н д S |
Частота попадания в группы |
Частость, % |
Отношение сглаженных частостей yA yB |
ДК |
Jрасч |
||||
|
вероятная |
сглаженная |
|||||||||
|
А |
В |
А |
В |
А |
В |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
-1 |
- |
0 |
0 |
0 |
0 |
4 |
1,5 |
- |
- |
- |
|
0 |
- |
0 |
0 |
0 |
0 |
10 |
5 |
- |
- |
- |
|
1 |
0,0-0,08 |
16 |
11 |
39 |
15 |
20 |
10 |
2,2 |
3 |
0,29 |
|
2 |
0,08-0,16 |
9 |
13 |
22 |
17 |
20 |
14 |
1,43 |
2 |
0,05 |
|
3 |
0,16-0,24 |
5 |
8 |
12 |
11 |
15 |
13 |
1,15 |
1 |
0,01 |
|
4 |
0,24-0,32 |
4 |
11 |
10 |
15 |
11 |
11 |
1 |
0 |
0 |
|
5 |
0,32-0,40 |
1 |
2 |
2,4 |
2,7 |
6 |
6 |
1 |
0 |
0 |
|
6 |
0,40-0,48 |
4 |
2 |
10 |
2,7 |
6 |
5 |
1,2 |
1 |
0,01 |
|
7 |
0,48-0,56 |
1 |
5 |
2,4 |
7 |
4 |
5 |
0,8 |
-1 |
0,01 |
|
8 |
0,56-0,64 |
1 |
3 |
2,4 |
4 |
2 |
5 |
0,4 |
-4 |
0,06 |
|
9 |
0,64-0,72 |
0 |
4 |
0 |
5 |
0,7 |
5 |
0,14 |
-8 |
0,18 |
|
10 |
0,72-0,80 |
0 |
4 |
0 |
5 |
0,2 |
6 |
0,03 |
-15 |
0,45 |
|
11 |
0,80-0,88 |
0 |
4 |
0 |
5 |
0 |
6 |
0 |
- |
- |
|
12 |
0,88-0,96 |
0 |
8 |
0 |
11 |
0 |
6 |
0 |
- |
- |
|
41 |
75 |
100,2 |
100,4 |
100,0 |
98,5 |
- |
- |
J=1,05 |
||
Таблица 3. Расчёт информативности для признака 3
|
а 5 S а О У * и S |
& н в S |
Частота попадания в группы |
Частость, % |
Отношение сглаженных частостей yA yB |
ДК |
J расч |
||||
|
вероятная |
сглаженная |
|||||||||
|
А |
В |
А |
В |
А |
В |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
-1 |
- |
0 |
0 |
0 |
0 |
2 |
0 |
- |
- |
- |
|
0 |
- |
0 |
0 |
0 |
0 |
6 |
1 |
- |
- |
- |
|
1 |
0,0-50 |
7 |
0 |
17 |
0 |
14 |
3 |
5,50 |
7 |
0,63 |
|
2 |
50,1-100 |
12 |
8 |
29 |
11 |
20 |
8 |
2,50 |
4 |
0,24 |
|
3 |
100,1-150 |
7 |
11 |
17 |
15 |
17 |
12 |
1,40 |
1 |
0,02 |
|
4 |
150,1-200 |
5 |
7 |
12 |
9 |
12 |
12 |
1,00 |
0 |
0 |
|
5 |
200,1-250 |
2 |
12 |
5 |
16 |
7 |
13 |
0,54 |
-3 |
0,09 |
|
6 |
250,1-300 |
0 |
7 |
0 |
9 |
4 |
12 |
0,33 |
5 |
0,20 |
|
7 |
300,1-350 |
2 |
10 |
5 |
13 |
5 |
12 |
0,42 |
-4 |
0,14 |
|
8 |
350,1-400 |
4 |
9 |
10 |
11 |
5 |
9 |
0,56 |
-2,5 |
0,05 |
|
9 |
400,1-450 |
0 |
4 |
0 |
5 |
3 |
6 |
0,50 |
-3 |
0,05 |
|
10 |
450,1-500 |
1 |
0 |
2 |
0 |
2 |
3 |
0,67 |
-2 |
0,01 |
|
11 |
500,1-550 |
0 |
2 |
0 |
3 |
1 |
3 |
0,33 |
-5 |
0,05 |
|
12 |
550,1-600 |
1 |
3 |
2 |
4 |
1 |
2 |
0,50 |
-3 |
0,01 |
|
13 |
600,1-650 |
0 |
1 |
0 |
1 |
0,4 |
2 |
0,20 |
-7 |
0,06 |
|
14 |
650,1-700 |
0 |
1 |
0 |
1 |
0,2 |
1 |
0,20 |
-7 |
0,03 |
|
41 |
75 |
99,0 |
99,6 |
99,0 |
99,0 |
J=1,58 |
||||
Т аблица 4. Расчёт информативности для признака 4
|
OS а § § а О У * и S |
аа н д S |
Частота попадания в группы |
Частость, % |
Отношение сглаженных частостей y A y B |
ДК |
J расч |
||||
|
вероятная |
сглаженная |
|||||||||
|
А |
В |
А |
В |
А |
В |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
-1 |
- |
0 |
0 |
0 |
0 |
1 |
2 |
- |
- |
- |
|
0 |
- |
0 |
0 |
0 |
0 |
5 |
9 |
- |
- |
- |
|
1 |
0-7 |
4 |
19 |
10 |
25 |
12 |
20 |
0,58 |
-2 |
0,13 |
|
2 |
7-14 |
13 |
32 |
32 |
43 |
18 |
27 |
0,67 |
-2 |
0,09 |
|
3 |
14-21 |
5 |
14 |
12 |
19 |
16 |
21 |
0,76 |
-1 |
0,02 |
|
4 |
21-28 |
5 |
6 |
12 |
8 |
15 |
12 |
1,25 |
1 |
0,02 |
|
5 |
28-35 |
7 |
2 |
17 |
2,7 |
12 |
5 |
2,40 |
4 |
0,14 |
|
6 |
35-42 |
3 |
0 |
7 |
0 |
9 |
1,4 |
6,40 |
8 |
0,32 |
|
7 |
42-49 |
2 |
0 |
4,9 |
0 |
5 |
0,6 |
8,30 |
9 |
0,20 |
|
8 |
49-56 |
0 |
0 |
0 |
0 |
2 |
0,6 |
3,30 |
5 |
0,03 |
|
9 |
56-63 |
0 |
2 |
0 |
2,7 |
1 |
1,2 |
0,83 |
-1 |
0,00 |
|
10 |
63-70 |
0 |
0 |
0 |
0 |
1 |
0,5 |
2,00 |
3 |
0,01 |
|
11 |
70-77 |
2 |
0 |
49 |
0 |
2 |
0,3 |
6,67 |
0,07 |
|
|
41 |
75 |
99,8 |
100,4 |
99,0 |
100,6 |
- |
- |
J=1,03 |
||
Список литературы Модель информативности данных на основе пакетов прикладных программ для нефтегазовой отрасли
- Дисперсионный анализ. - [Электронный ресурс]. - Режим доступа: http://statsoft.ru/home/textbook/modules/stanman.html#basic (дата обращения 15.01.2023).
- Таранчук В. Б. Основные функции систем компьютерной алгебры. - Минск: БГУ, 2013. - 59 с.
- Фомин Я.А. Распознавание образов: теория и применения. - 2-е изд. - М.: ФАЗИС, 2012. - 429 с. - 978-5-7036-0130-4.
- ISBN: 978-5-7036-0130-4
- F-Test for Equality of Two Variances. - [Электронный ресурс]. - Режим доступа: https://www.itl.nist.gov/div898/handbook/eda/section3/eda359.htm (дата обращения 15.01.2023).
- Kullback S. Information Theory and Statistics. - John Wiley & Sons, 1959.


